大气湿球温度计算的牛顿迭代法

潘晓春，程春龙

(江苏省电力设计院，江苏 南京 211102)

1 概述

最近5年炎热季节10%湿球温度及相应气象条件，是电厂冷却塔热力计算不可或缺的重要参数。我国许多气象观测站于2002年～2005年间陆续停止了湿球温度的观测，给电厂冷却塔设计带来了一定的困难。

当气象站缺乏实测湿球温度资料时，可用气象学公式法、查表法、气象要素相关法、差值法等多种方法推算湿球温度，推荐按气象学公式计算湿球温度，查算结果与实测值存在一定的偏差，使用时注意进行适当修正。文献[2]采用EXCEL宏实现湿球温度的求解。文献[3]分别设计了逼近法和多元回归法估计湿球温度。文献[4]通过论证饱和水汽压函数的单调性，提出递减法计算湿球温度法。文献[5]建立了基于LM－BP神经网络的湿球温度计算模型。

2 干、湿球温度的基本公式

干湿球测湿的结构原理是在温度表的水银球体包上脱脂纱布，纱布的下端浸入盛水的容器中，纱布在毛细管作用下经常处于湿润状态，此温度计称为湿球。湿球纱布中的水分必然向空气中蒸发，即在湿球与通过湿球的空气之间发生湿交换。水的蒸发量与空气中的水汽压平衡并使湿球温度维持在一定的数值。如果再用一支温度计测量当时的干球(此温度计称为干球温度计)，就可以利用干湿球温度的差值和其它测量条件来计算空气中的水汽压。

基于道尔顿蒸发定律和热量守恒原理，根据牛顿热传导公式等可以导出空气中的水汽压与干湿球温度、大气压力等的关系：

式中：td为干球温度，(℃ )；tw为湿球温度，(℃ )；e为水汽压，(hPa)；P为气压，(hPa)；A为干湿表系数(℃-1)，由干湿表类型、通风速度及湿球结冰与否而定；Etw为湿球温度tw对应的纯水平液(冰)面饱和水汽压，(hPa)。

空气中相对湿度按下式计算：

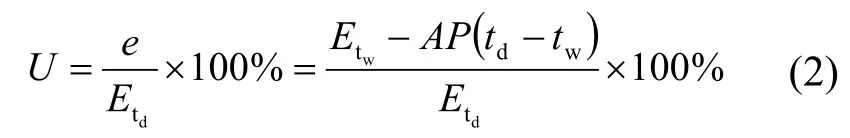
式中：U为相对湿度，(%)；Etd为湿球温度td对应的纯水平液(冰)面饱和水汽压，(hPa)。

3 重要参数的取值

在空气调节领域中，研究湿空气的有关参数普遍应用的是Hyland－Wexler公式(Hyland and Wexler 1983b)；泰登(Tetens)公式和马格努斯(Magnus)公式因为其形式简便，在物理学中也常常使用；纪利经验公式则常在给排水中有关工况的计算中使用，例如求冷却塔的冷却效率；Buck[1996]公式是Buck[1981]的改进公式，这个公式在国内并不常用；Marti Mauersberger公式是唯一以170 K时水蒸汽压力实际测量值为基础的经验公式。

周西华等采用比较相对误差的方法，将国内外常用的计算饱和水蒸汽分压力的经验公式与戈夫－格雷奇(Goff－Gratch)公式进行分析，认为戈夫－格雷奇公式最为准确，建议我国空气参数计算时采用戈夫－格雷奇公式。该文还认为，0℃以下的低温计算时，可使用Buck[1996]公式与Marti Mauersberger 公式；0～120℃范围内进行计算时，也可使用Buck[1996]公式与纪利公式；在常温20～40℃范围内进行精确的计算时应选用戈夫－格雷奇公式、泰登公式和纪利公式。

戈夫－格雷奇饱和水汽压公式由Goff(1957)最早提出，自1947年起就为世界气象组织(WMO)推荐公式，是以后多年世界公认的最准确的计算公式，也是我国现行观测规范和环境试验等规定采用的公式。本文采用戈夫－格雷奇饱和水汽压公式计算，即

(1)纯水平液面饱和水汽压(温度范围－49.9℃～+49.9℃)：

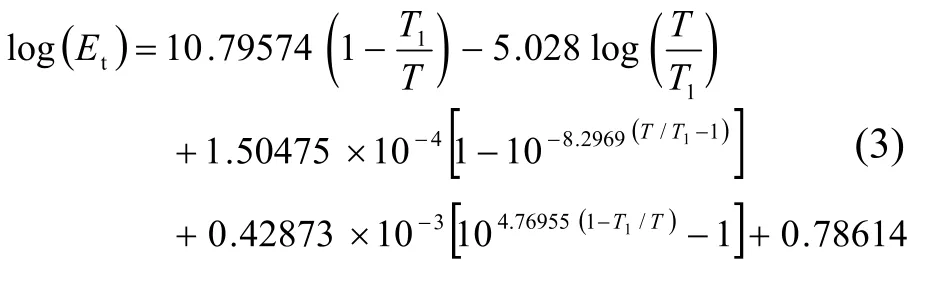
(2)纯水平冰面饱和水汽压(温度范围－79.9℃～－0.0℃)：

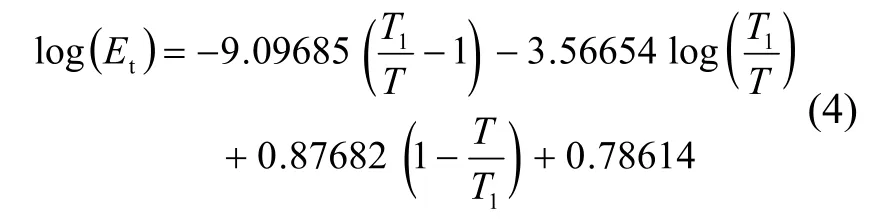
式中：T1为水的三相点温度，T1=273.16 K；T为绝对温度，对于求算Etw，T=Ew+273.15 K；对于求算Etd，T=Ed+273.15 K。

在计算的炎热季湿球温度时，建议采用与风速有关的关系式计算A值，这样就考虑了风速对湿球温度的影响，在没有风速资料的情况下，建议采用A=0.7947×10-3，这就与国内气象站的测湿工具测出的结果一致。

4 牛顿迭代算法

为推求湿球温度，将式(1)整理为

湿球温度对应的饱和水汽压函数中包含湿球温度的指数和对数，且式(5)等号两边均含有待求的湿球温度，函数关系复杂，难以直接求解湿球温度。本文采用牛顿迭代法求解。

令

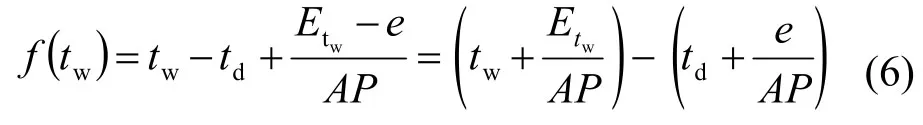
欲求tw，等价于求解方程f(tw)=0的根。构造一个基于Taylor展开的牛顿迭代公式。

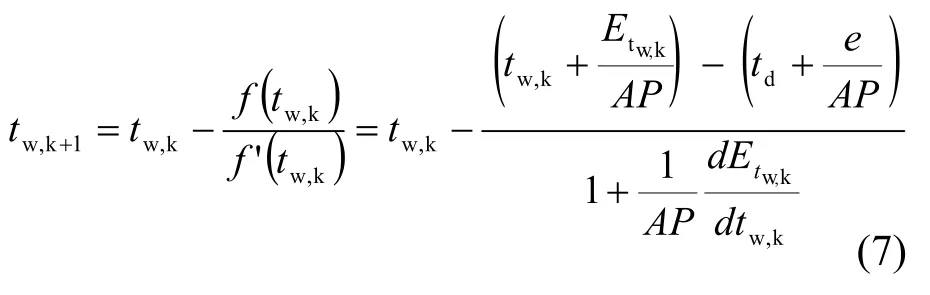
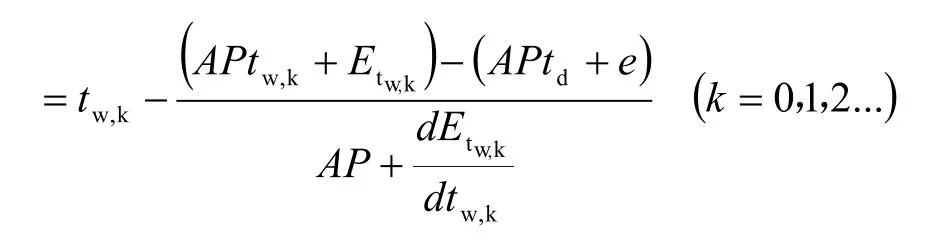
据式(3)和式(4)，分别对tw求导：

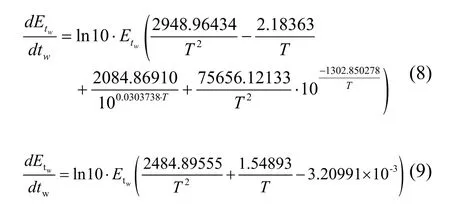
至此，对于求解最炎热季节日均湿球温度，即可利用式(7)、式(3)以及式(8)联合迭代求解。

根据计算实践，tw的迭代初值取td，成果误差取0.001℃，一般只需迭代3～4次即可结束。当需要批量计算时，宜编程计算，即便利用EXCEL列表迭代计算也不显繁琐。

在工程实践中，有时没有搜集到日均水汽压，而只搜集到日均相对湿度，此时可将式(2)变化为e=U·Etd/100，进而代入式(7)即可。

5 算例与误差分析

(1) 成果的精度评定标准

下文算例采用确定性系数来评价计算结果的精度：

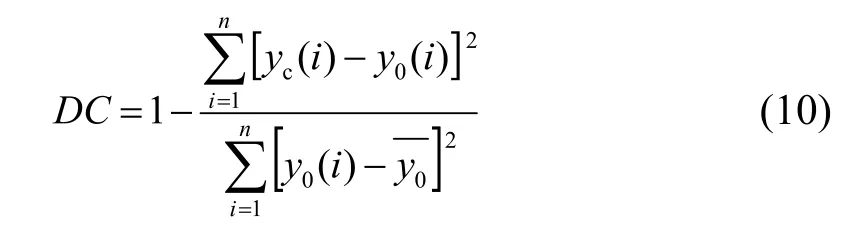
式中：DC为确定性系数；y0(i)为实测值；yc(i)为计算值；为实测值的均值；n为资料序列长度。

(2) 多站计算成果的精度评价

分别采用徐州、连云港、淮安、南通、无锡气象站2000年7月1日～2000年8月31日逐日平均干球温度、平均气压、平均水汽压，按照前文所述牛顿迭代法计算逐日平均湿球温度，并采用确定性系数评价上述5座气象站湿球温度的计算成果精度。

表1 各气象站湿球温度计算成果精度统计

由表1可见，无锡站、连云港站计算成果的确定性系数稍低，分别为0.9369和0.9714，其余3站计算成果的确定性系数均极高，均在0.999以上，显示了本文提出的计算方法具有较高的精度。

(3) 采用相对湿度与采用水汽压的计算成果的比较

采用南京气象站1999年6月1日～8月31日、2000年6月1日～8月31日合计184组逐日平均干球温度、平均气压、平均水汽压、平均相对湿度等气象要素，分别以水汽压和相对湿度代入按前文所述牛顿迭代法计算逐日平均湿球温度，并与湿球温度实测值进行比较分析。

分别以水汽压和相对湿度代入计算的湿球温度与湿球温度实测值分别绘制图1和图2。

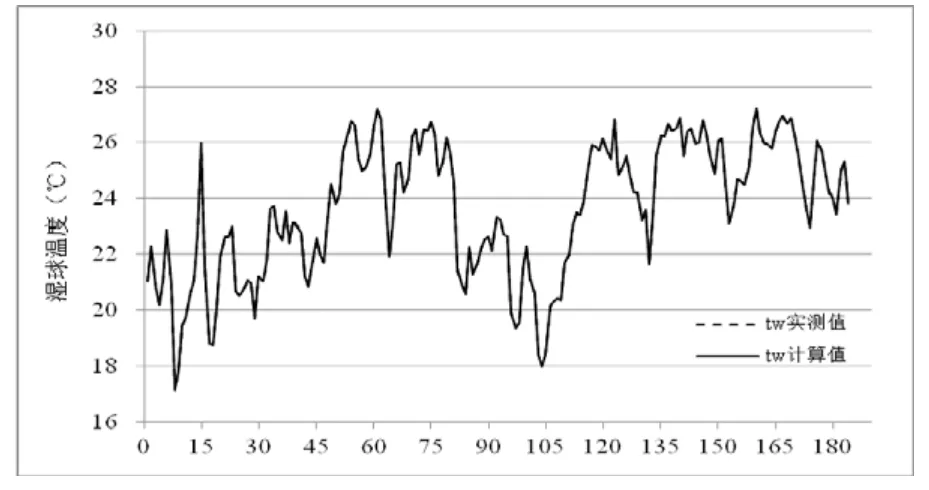
图1 以水汽压代入计算的湿球温度与湿球温度实测值比较图

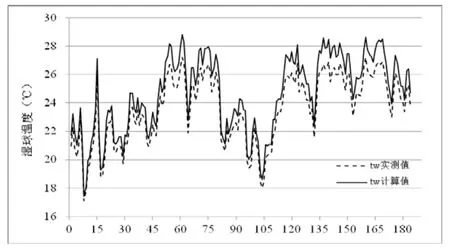
图2 以相对湿度代入计算的湿球温度与湿球温度实测值比较图

采用确定性系数评价两种代入资料的计算成果精度，见表2。

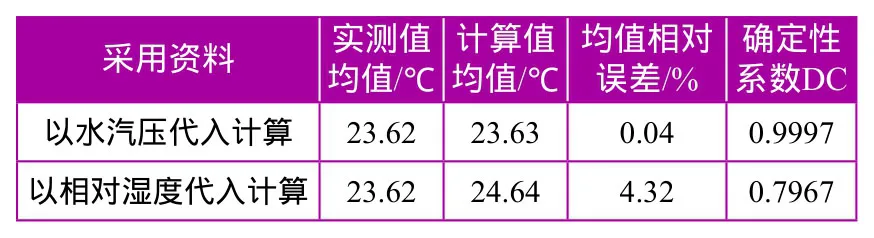
表2 南京气象站湿球温度计算成果精度统计

由表2、图1和图2可知，与湿球温度实测值相比，以水汽压代入计算的湿球温度成果的确定性系数远高于以相对湿度代入计算的湿球温度成果的确定性系数，表明前者具有较高的计算精度。

实质上，以相对湿度等来计算湿球温度与以水汽压来计算湿球温度理应具有同等的精度。出现上述现象的根源主要在于由于气象站观测提供的相对湿度大多为保留一位小数的百分数，甚至仅仅是整数的百分数，含有较大的舍入误差，精度较低，由此计算的湿球温度精度当然相对较低。

6 结语

(1)本文提出的湿球温度计算的牛顿迭代法具有迭代速度快、成果精度高以及适用范围广等优点，不仅可用于计算炎热季节湿球温度计算，对于其它包括结冰的冬季同样适用。

(2)实质上，以相对湿度等来计算湿球温度与以水汽压来计算湿球温度理应具有同等的精度，但因气象站观测提供的相对湿度含有较大的舍入误差，由此计算的湿球温度精度相对较低。因而，应尽量采用水汽压的实测值而非相对湿度来计算湿球温度。

(3)本文算例采用的验证气象站均位于我国南方地区，而对于比较干燥的北方地区，关于精度或误差的分析结论仍有待进一步验证。

[1]DL/T5158－2012，电力工程气象勘测技术规程[S]．

[2]赵永胜，刘德平，胡长权．无资料地区湿球温度计算方法研究[J]．电力勘测设计，2009，(5)．

[3]王海军．两种湿球温度估计方法比较及误差分析[J]．气象，2011，(04)．

[4]李志龙，等．递减法求解湿球温度[J]．电力勘测设计，2012，(1)．

[5]林婵，王起峰，朱良山．基于LM－BP神经网络的湿球温度计算模型[J]．水电能源科学，2013，31(1)．

[6]周西华，等．饱和水蒸汽分压力经验公式的比较[J]．辽宁工程技术大学学报，2007，26(3)．

[7]QX/T60－2007，地面气象观测规范第16部分：地面状态观测[S]．

[8]GB/T6999－1986，环境试验用相对湿度查算表[S]．

[9]GB/T11605－2005，湿度测量方法[S]．