大跨度斜拉桥测量控制技术

2015-03-21祝贤洲

科技资讯 2015年31期

祝贤洲

摘要：斜拉桥是现代大跨度桥梁的主要桥型，其优点是跨越能力强，桥型美观。随着施工技术的发展进步，斜拉桥的跨度不断变大。在跨度的加大和主塔的升高同时，相应的对施工测量提出了更高的要求。怎样保证在测量难度大的情况下，还能保证测量精度，确保符合设计要求，这就要在整个施工测量过程中采取必要的、确实可行的测量方法和技术。

关键词：斜拉桥大跨度测量控制技术

中图分类号：U446 文献标识码：A 文章编号：1672-3791（2015）11（a）-0062-05

斜拉桥是现代桥梁体系中崭新的桥型，斜拉桥作为一种拉索体系，比梁式桥的跨越能力更大，是大跨度桥梁的最主要桥型，同时斜拉桥也是一种重要的景观桥。斜拉桥是超高静定结构，它对成桥的线形有较严的要求，每个节点坐标的变化都会影响结构内力的分配。桥梁线形一但偏离设计值，将导致内力偏离设计值。现代斜拉桥的跨度一般超过200 m，主塔高度超过100 m，目前世界最大跨度斜拉桥是位于俄罗斯远东城市弗拉迪沃斯托克的俄罗斯岛大桥，大桥主跨达1104 m，主塔高度324 m。因此在桥梁建设过程中，必须采用有效的施工测量方法，提高测量精度，确保大桥建设质量。

1 前期施工中的主要测量技术

1.1 控制网网型与点位的选择

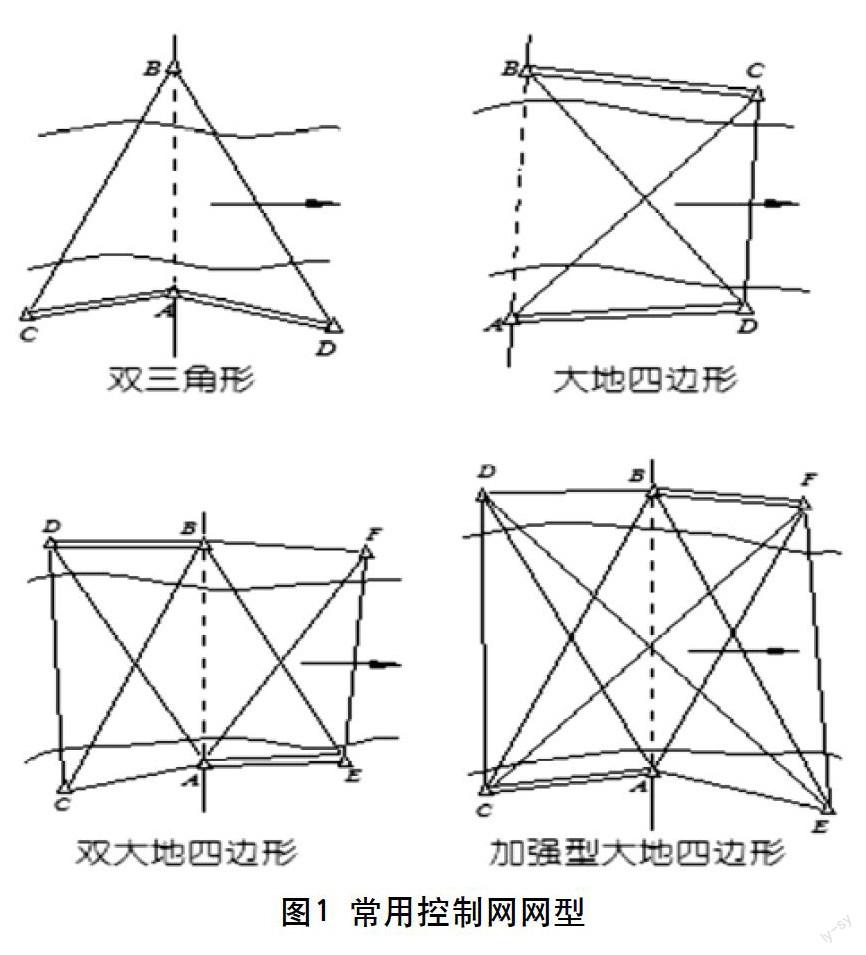
在主体工程开工之前，为了便于施工阶段的测量观测，同时为了有效提高测量效率和精度，建立合适的施工控制网是非常有必要的。控制网的网型一般选用大地四边形或三角形，以控制跨越江河部分的主桥为主。在满足桥轴线长度测定和墩台中心定位精度的前提下，力求图形简单并具有足够的强度，以减少外业观测工作和内业计算工作。根据精度要求和地形条件，桥梁施工平面控制网的网形布设有以下几种形式（见图1）。

控制点的点位选择尤为重要，一般选择在边墩上下游的位置。观测的时候竖直角不宜大于20°，因此必须确定控制点到主桥主塔的最小距离。考虑到仪器激光对中误差可达2 mm，因此主塔施工用控制点常用强制对中墩来减少对中误差[1]，其对中误差<=0.2mm。

2 主塔施工测量

2.1 斜拉桥塔柱的结构样式

现代斜拉桥的主塔柱样式多种多样，但基本的最长用结构样式有“A”型塔柱，倒“Y”型，“H”型，其他一些类型都是通过这几个基本类型演变而来（如图2～4）。

2.2 主塔施工测量的仪器设备选择

根据设计要求，进行测量放样的精度分析来确定测量设备的精度要求，进行测量设备的配置。斜拉桥施工测量一般采用0.5″的全站仪（如徕卡的高精度全站仪TS30），如果条件允许也可以考虑使用1″的仪器。

2.3 主塔施工测量

主塔塔柱一般由下塔柱、横梁、中塔柱和上塔柱组成。塔柱侧面通常有一定的倾斜度，其平面位置随着高程的变化而变化。为了控制好主塔的倾斜度以及垂直度，需在每个节段每个特征点调整好其平面尺寸位置。操作时，先测量其节段高程，然后根据实测高程进行理论平面位置推算，进而进行测量控制。

由于塔柱的平面位置与高程和斜率成一次函数关系，可根据设计图纸推算出塔柱在H高程处的平面位置。

X=f1（h，i）+X0

Y =f2（h，i）+Y0

h =H -H0

i为斜率，X0，Y0为塔柱平面位置基准起算坐标。将实测坐标与计算的理论坐标进行比较，调整模板到理论位置。

为减少日照对塔柱变形的影响，塔柱各部位和各构件的施工测量和放样，应根据多日温度观测记录，选择在不受日照影响和气温变化较小的时间段进行。塔柱施工宜采用焊接的型钢劲性骨架辅助定位等措施确保精确定位，以保证在测量、放样、立模、钢筋和管道定位的精度。

一般情塔柱都是分节段施工，为控制好塔柱的倾斜度与垂直度，保证主塔分段浇筑时节段与节段间衔接顺直，不出现错台，每一节段浇筑完毕，应在此段塔柱顶面对该节段的结构尺寸及轴线偏位进行竣工测量，并在面四边做出中点标志及标高标志，作为下一节段模板调整的依据。同时，必须对墩柱的垂直度、斜率进行观测，保持外表面的顺直，不允许出现折线。还要定期对塔柱顶面纵、横两个方向的偏位值进行连续跟踪观测，通过观测数据的规律变化，确定在自然条件下塔柱纵、横向偏移的变化规律，以确定下一工序如何修正偏位情况，将塔柱倾斜度、垂直度控制在允许的范围内。

3 索道管定位测量

斜拉桥索道管定位是斜拉桥高塔柱施工中一项测量精度要求很高（一般要求平面5 mm以内，高程±10 mm以内）、测量难度极大的工作，斜拉桥索道管的位置及其角度均应准确控制，锚板与索道管必须互相垂直，并符合图纸要求，根据设计要求和斜拉索的结构受力特性，索道管的定位应优先保证其轴线精度，其次才是锚固点位置的三维精度。索道管轴线与斜拉索轴线的相对偏差主要由索道管两端口中心的相对定位精度决定。

3.1 定位模型的建立

斜拉桥索道管的定位质量决定了斜拉索的空间位置，也直接影响着主梁的线型。为了保证主梁索道管与主塔索道管的相对位置关系，要求主梁与主塔索道管的定位必须以同一基准为依据。

依据设计图纸给出的索道管参数，将斜拉索中心线分别向XOZ面及XOY面投影，计算出投影后的截距及斜率，由此可归纳出斜拉索中心线的空间直线方程L0：

X0为自变量，可表示斜拉索中心线上某一点的里程X坐标，Y0、Z0是与X0相对应的点在三维坐标系中的Y及Z值，YX0、ZX0、a、b分别为斜拉索中心线投影到XOZ及XOY面上的截距及斜率。

3.2 主塔索道管定位方法

主塔索道管定位一般按先粗定位，然后再精调两步进行。粗定位前，先将索导管的下底面线用墨线弹出，然后在前后竖直的劲性骨架上搭焊两根角钢（见图5）。

焊接角钢前，先测出劲性骨架的X坐标，根据索导管下底面线性关系反算出对应X坐标下的Y、Z坐标，根据Z值进行角钢焊接，在进行角钢焊接时，角钢的高度统一适当放低1～2 cm，以便索道管高程精调。角钢焊接好之后，在角钢的顶面放出索道管的Y方向，并做记号。索道管吊装时，注意将索道管的底面线与角钢上的点重合。

索道管粗吊装好之后进行索道管精调。精调时，首先对锚固点进行精调。利用倒链将锚固点精调到位，然后再利用倒链对索道管出塔处进行调整。出塔点调整时，根据索道管轴线方程，利用实测里程（X坐标）进行设计高程推算，进行上下调整，同样进行Y坐标左右调整。出塔点调好之后，再对锚固点进行复测、调整，直至锚固点和出塔点同时满足定位要求，然后对索道管进行加固。

由于索道管的定位精度由其轴线精度决定，所以在进行索道管精调时，优先保证索道管的轴线位置精度，即保证索道管两端口中心的相对定位精度。常规的索道管定位采用间接定位法，即根据索道管的顶面线或底面线进行定位，但是，受索道管上附着物（螺旋筋、加紧钢板、附着钢筋等）影响，上下特征线将不方便或不能够准确寻找。为了解决索道管的定位问题，可根据索道管的尺寸以及外形特征对索道管的锚固端以及出塔处加工专门的定位板（见图6、7）。

使用时，锚固端定位板直接放置在锚垫板上，直接观测定位板中心即锚固点中心坐标，进行锚垫板位置的调整定位；出塔处，将出塔定位板放置于索道管开口处，注意使定位板的半圆弧与圆杆下侧同索导管的内壁同时紧贴，后观测定位板中心即索道管出口处中心坐标，对索道管出口位置进行调整定位（见图8、9）。

3.3 主梁索道管定位方法

考虑到主桥的活载，主梁施工时的施工线形与设计成桥线形有一定的预抬量，对主梁的索道管测量定位时必须考虑这预抬量，使得成桥后索道管位置满足设计要求。主梁索道管定位时，先根据设计部门计算的预抬量△Z，在平面位置保持原设计值不变的前提下，只是将主梁索道管在竖向整体抬高△Z，即可解决预抬量对索道管定位的影响（如图10所示）。

3.4 索道管定位过程中应注意的事项

在进行索道管定位时由于索塔砼受到日照、索塔砼内部温度不均、风力等因素影响，上塔柱位置发生随机的变化。在进行索道管高精度定位时，要选择合适的测量时间，在没有日照、没有3级以上大风、并且空气温度及索塔温度变化不大的时段里进行索道管高精度定位。因此一般情况下宜选择在夜里10点到第二天早上5点进行测量定位作业，以减弱索塔变形对索道管定位精度的影响。

在索道管及上塔柱精确定位测量时很难做到对向观测，用三角高程测量传递高程，且测量点平距大于200 m时，要尽量消除球气差对高程的影响，可利用球气差改正公式进行改正[2]：。k为折光系数[3]，一般取值0.14～0.16之间，D为到测点的平距，R为地球半径。

4 塔梁同步施工中的监控测量

4.1 塔梁同步施工技术

现代斜拉桥的混凝土主塔通常较高，施工时分阶段浇筑施工，因此施工时间较长。为了尽量缩短桥梁建设时间，一种新的施工技术，塔梁同步施工出现了。即在主塔未施工完的情况下，边施工主塔边施工主梁，并进行斜拉索挂索（见图11）。

4.2 塔梁同步施工中主塔的测量监控

采取塔梁同步施工技术时，由于主塔两侧主梁重量不完全相等、桥面临时荷载偏载、张拉斜拉索控制索力的油压表以及张拉系统的误差等因素，导致索塔受不均匀水平力，索塔很可能出现较大的偏位（如图12所示），对于后续主塔节段的施工造成很大的困难，因此，针对塔梁同步施工这种新的施工技术，也应采用相应的测量控制方法，使得后续索塔在施工完毕后，最终的索塔在自然受力状态下是顺直的。

为了精确观测塔柱的变形情况，并依据测量数据分析判断塔柱偏位的趋势，就需要在塔柱上合适的位置埋设监测点。监测点通常由一序列的棱镜固接在需要观测偏位情况的已浇筑节段外侧壁的观测装置。塔柱监测点一般从中塔柱开始随着塔柱施工由下至上在需要观测的节段布置。通常上塔柱在每节段顶部塔柱侧壁上均埋设一层监测点，每层埋设4套监测点，即在一个节段的4个角布置观测点，便于在主塔两侧均能监测到主塔的变形情况。监测点埋设要牢固可靠，确保每次的观测数据真实可信。

理想状况下，索塔处于铅垂状态，当索塔受不均匀水平力的作用时，其产生水平变形，变形曲线为抛物线，顶点在塔根部，变形截止点是水平力施加点。水平力施加点以上部分，在不考虑自重前提下，是沿该点抛物线切线方向延伸。建立塔柱偏位模拟数学模型，其抛物线一般方程为：d=kh2，其中k为常数，可以根据多组观测数据求出，h为高程，d 为索塔偏离值。

在实际施工过程中，在主塔两侧不同部位埋设固定监测点，当索塔受不均匀水平力作用时，观测多组数据（h1，d1）、（h2，d2）……（hn，dn），根据建立的数学模型，可以计算出常数k1、k2…… kn ，建立矩阵VT=[k1 k2…… kn]，根据最小二乘原理，VTV=最小，可以解算出常数k的最或是值。由于所有的观测值均使用同一台仪器，且由同一人观测，所以一般认为所获取的数据是同精度观测，且服从正态分布，因此，在实际计算过程中，可以取k1、k2…… kn的平均值作为常数k的最或是值，即

k=（k1+k2+……+kn）/n

以上过程根据建立的数学模型和实际观测值，确定了索塔受不均匀水平力所产生的变形的曲线方程。

为确定待浇节段的实际施工位置，还须求得切线方程，根据数学模型d= kh2，通过数学方法可以得出通过抛物线上的点（h0，d0）的切线方程为：d=2*k*h0*（h-d0）。

用数学方法同样可以得出，在切线上距点（h0，d0）距离为L的待求点（h1，d1）的计算公式。

其中m为所求出的常数，m=2kh。

以上所求坐标（h1 ，d1）即是索塔在受不均匀水平力作用在点（h0，d0）时，距作用点距离为L的待求点的坐标（h为高程，d为索塔偏离值）。

4.3 塔梁同步施工模拟计算过程实例分析

武汉二七长江大桥的建设过程中为了缩短工期，主塔即是采用的塔梁同步施工技术。主塔施工时测得的实测数据如下：第6节顶（47.5 m处）位移2 mm；第16节顶（107.5 m处）位移19 mm；第25节顶（159.9 m处）位移46 mm；第26节顶（165.9 m处）位移50 mm；根据以上实测数据进行第29节段塔柱模板定位计算（29节顶距26节顶距离为18 m）。以塔根部（13.5 m处）作为0位移位置。

根据方案公式计算k值。

1.7 301×10-6

2.15 029×10-6

2.14 623×10-6

2.15 278×10-6

2.01 485×10-6

165.9 m处抛物线切线斜率

2.04 485×10-6×152.4=6.2 327 028×10-4

计算29节模板顶面坐标：

这样就根据第26节模板顶面的预偏计算出第29节模板立模时需要的预偏量及高程。

5 结语

现代大型桥梁建设对测量的精度要求越来越高，该文讨论了斜拉施工中的主要测量技术，在斜拉桥施工中对测量精度要求较高的施工部位的测量方法进行了分析。实践证明，对于测量难度较大，精度要求高的测量工作，采取合适的测量方法，可以有效地提高测量精度和效率，减少计算量，降低测量工作强度。