求解复合型Tschebycheff方程一类边值问题的相似构造法
2015-03-21夏文文李顺初桂东冬
夏文文, 李顺初, 桂东冬
(1.西华大学 应用数学研究所, 四川 成都 610039;2.北京东润科石油技术股份有限公司, 北京 100029)
求解复合型Tschebycheff方程一类边值问题的相似构造法
夏文文1, 李顺初1, 桂东冬2
(1.西华大学 应用数学研究所, 四川 成都 610039;2.北京东润科石油技术股份有限公司, 北京 100029)
针对复合型Tschebyscheff方程的一类边值问题,研究了其解的结构,发现该边值问题解的表达式可以通过Tschebyscheff方程的两个线性无关解(Tschebyscheff多项式和第二类Tschebyscheff函数)和边值条件、交界面条件的系数组装得到,并提出求解该类边值问题的一个新解法——相似构造法。
复合型Tschebyscheff方程组; 边值问题; 相似结构; 相似核函数; 相似构造法
近年来,学者对一些微分方程具有某类边值问题的解进行了广泛的研究[1-4],发现其解具有相似的表达式,并给出了构造这种相似结构式的具体步骤,提出了构造这种相似解式的方法——相似构造法。文献[4]讨论了一般型Tschebyscheff方程边值问题解的相似结构,本文对复合型Tschebyscheff方程的一类边值问题的解进行了研究,通过对复合型边值问题解的表达式进行整合,获得了其解的相似结构。
本文研究如下边值问题:
(1)
其中:D,E,F,G,H,a,b,n1,n2为已知实常数,且D≠0,G2+H2≠0,0 在本文中,首先将给出两个引理,其次将会论证基本定理并得到4个推论,最后总结出相似构造法的具体步骤。 yi=AiTni(x)+BiUni(x), (2) 其中,Ai,Bi为任意常数,Tni(x)是Tschebyscheff多项式,Uni(x)是第二类Tschebyscheff函数。 引理2 对于二元函数 (3) 有: (4) (5) (6) 其中i=1代表左区(a 证明 根据Tschebyscheff多项式和第二类Tschebyscheff函数的递推公式[5]: 即可证得(4)式。同理可证(5)、(6)式。 定理 若边值问题(1)有唯一解,则其左区(a (7) 右区(c (8) 其中Φ*(x)称为右(区)相似核函数: (9) Φ(x)称为左(区)相似核函数: (10) (11) A1Tn1(c)+B1Un1(c)-A2αTn2(c)-B2αUn2(c)=0, (12) A1n1[Tn1-1(c)-cTn1(c)]+B1n1[Un1(c)-cUn1(c)]- A2n2β[Tn2-1(c)-cTn2(c)]-B2n2β[Un2(c)-cUn2(c)]=0, (13) (14) 联立(11)—(14)式,得到以A1,A2,B1,B2为待定系数的方程组,由边值问题(1)有唯一解知该方程组系数行列式Δ≠0,且 (15) 求解线性方程组(11)—(14),得 (16) (17) (18) (19) 将(16)—(19)式代入(2)式,并利用相似核函数(9)、(10)的表达式,便可得到边值问题(1)的左、右区解的表达式(7)、(8)式。 推论1 对于边值问题(1),若右边界条件中G≠0,H=0(即y2(b)=0),则(9)式简化为: 推论3 边值问题(1)的解式(7)和其导数有如下关系式: 推论4 边值问题(1)的左边界条件中,令E=0,D=1,则其左区间解为左区相似核函数: 求解复合型Tschebyscheff方程的边值问题,可以通过Tschebyscheff方程的两个线性无关解构造引解函数,再由引解函数和边界条件及交界面条件的系数按照上述步骤,就可较容易地求解此类边值问题,这种方法极大地简化了求解过程,提高了求解效率。 [1] 严娟,李顺初,邢承林.二阶欧拉方程的一类边值问题的相似结构[J].西华大学学报:自然科学版,2009,28(6):86-88. [2] 王芙蓉,李顺初,许东旭.Airy方程的一类边值问题的解的相似构造法[J].湖北师范学院学报:自然科学版,2013,33(1):79-85. [3] 黄荣军,李顺初,许东旭.求解第一种Weber方程边值问题的相似构造法[J].绵阳师范学院学报,2012,31(11):1-5. [4] 唐乙斌,李顺初,严娟,等.Tschebyscheff方程组边值问题解的相似结构[J].四川兵工学报,2011,32(1):155-156. [5] 刘式适,刘式达.特殊函数[M].北京:气象出版社,2002. [6] 陈珊丽,方金财,吴康.关于第一类切比雪夫型不等式的研究[J].湛江师范学院学报,2013,34(6):16-18. [7] 郑鹏社,李顺初,冷礼辉,等.一类非线性复合变型Bessel方程组边值问题的相似构造解法[J].信阳师范学院学报:自然科学版,2014,27(4):490-492. [8] 李顺初,王俊超,许丽.复合油藏球向渗流问题的解的相似结构[J].数学的实践与认识,2014,44(3):122-127. [9] 白丽霞,李顺初,桂东冬.复合型第二种Weber方程边值问题的新解法[J].中北大学学报:自然科学版,2014,35(6):633-637. [责任编辑:谢 平] Similar structured method of solution to boundary value of the composite Tschebyscheff system XIA Wen-wen1, LI Shun-chu1, GUI Dong-dong2 (1.Institute of Applied Mathematics, Xihua University, Chengdu 610039, China;2.Beijing Dongrunke Petroleum Technology Co.,Ltd., Beijing 100029, China) Based on the question of boundary value problem of composite Tschebyscheff system, this paper studies the structure of the solution, and it discoversthat the expression of solution of the boundary problem is acquired by structuring two linearly independence solutions of Tschebyscheff equation(Tschebyscheff polynomial and the second category Tschebyscheff function)and the coefficients of right boundary condition, left boundary condition and interface condition. The paper puts forward a new method of solving this class boundary value problem: the similar constructive method. composite Tschebyscheff system; boundary value problem; similar structure; similarity kernel function; similar structured metho 1673-2944(2015)02-0069-04 2014-12-31 四川省教育厅自然科学重点项目(12ZA164) 夏文文(1988—),男,陕西省石泉县人,西华大学硕士研究生,主要研究方向为微分方程及其应用;[通信作者]李顺初(1963—),男,湖北省浠水县人,西华大学教授,主要研究方向为微分方程和渗流力学及其应用。 O175.8 A1 主要定理及其证明
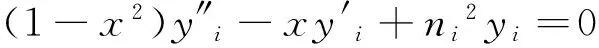

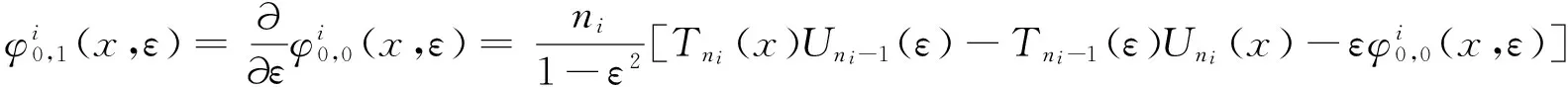
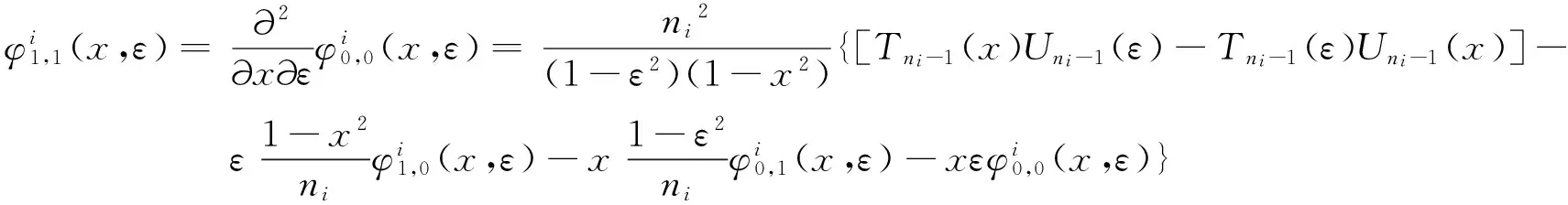
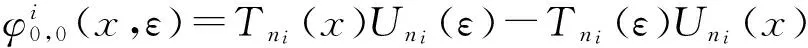
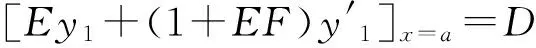
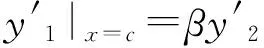
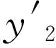
2 相似构造法步骤
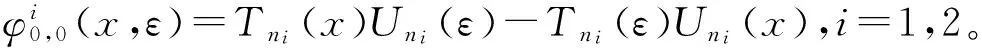
3 小 结
