防寒服填料吸湿性能影响因素模拟

丛 杉, 朱晓彧，王嫣雯

(上海工程技术大学，上海 201600)

防寒服填料吸湿性能影响因素模拟

丛 杉, 朱晓彧，王嫣雯

(上海工程技术大学，上海 201600)

文章根据Fick定律，建立纤维吸湿模型，采用有限差分法进行离散分析和Matlab编程语言进行了数值求解，针对纤维自身的物理属性以及外界相对湿度对纤维吸湿性能的影响进行模拟探究，通过对比分析证明模型的合理性。

羊绒；吸湿性能；影响因素；吸湿模型

1 前言

纤维的吸湿性能对纺织材料的各方面性能产生影响，如重量、长度、横断面、密度、机械性能、热学性质甚至光学性质等[1]。纤维对气相水分吸收的性质，主要取决于纤维中的大分子结构以及结晶状态，所以纤维吸湿作用就会受其微观结构的影响，纤维吸湿的微观机理如图1所示。除此之外，纤维的吸湿率还与环境温湿度有关，尤其是环境的相对湿度对纤维的吸湿性能影响较大，如图2所示。多层织物内部填充物的选用，会对防寒透湿性能产生影响。目前针对纤维水分测试的方法主要有两种：直接测试和间接测试[2]，应用最广泛的是烘箱法对纤维水分的测试法。但在实际的操作过程中存在一些弊端：干重与实际的纤维重量不符；在对材料进行反复测量时，外界条件的变化与影响会增加测量的误差；另外，测试的时间要维持在3 h左右，容易造成能源的浪费[3]。

从数值模拟角度，对纺织材料的影响进行研究是当前的应用热点。与传统的测试方法相比，吸湿模型能够提高研发效率，节约开发成本。吸湿模型主要借助分型理论，从微观形态建立纤维的吸湿模型。早前，陈天文等[4]在实验测试的基础上，建立织物放湿过程中表面温度与时间、过剩相对湿度的关系及过剩相对湿度与时间的关系模型。刘凌杰等[5]借助BET模型思想，建立了织物干基含水率模型，该模型与实验数据相吻合。李进等[6]采用归纳分析法，建立了非线性偏微分方程形式的织物动态吸湿模型，并在此基础上，提出了结构因子。但是以上模型，针对外界的影响因素考虑欠缺，仍然需要进一步改进。

图1 聚合物分子对水分的直接和间接吸着

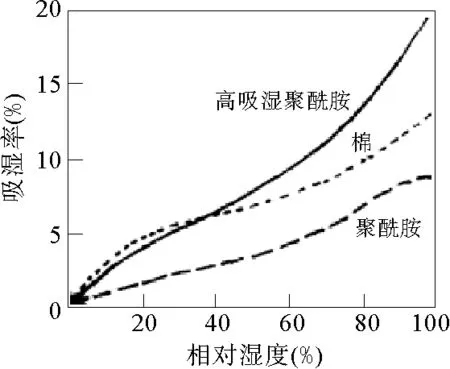
图2 纤维的吸湿率与相对湿度的关系

羊绒填料作为一种传统型的天然纺织材料，因为其自身细而且柔软，具有细、轻、柔、滑、糯、光、暖等优良性能[7]。羊绒、羊毛类填料以超强的保暖性和纯天然的质感，在各种防寒功能性纺织产品中，有着突出优势，能够满足人们对产品舒适性以及审美的需求。与羽绒填充物相比，羊绒的可塑性更强，在制作过程中，款式的变化更多，受到了不同年龄阶段消费者的欢迎。本文以羊毛、羊绒絮填料为研究对象，在Fick定律的基础上，建立纤维的吸湿模型，模拟纤维内部的水蒸气含量的变化情况，分析织物性能与外界环境对其所造成的影响。并在此基础上，提出相关的模拟软件开发。

2 纤维吸湿模型

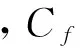
(1)

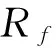
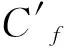
(2)

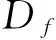
(3)

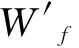
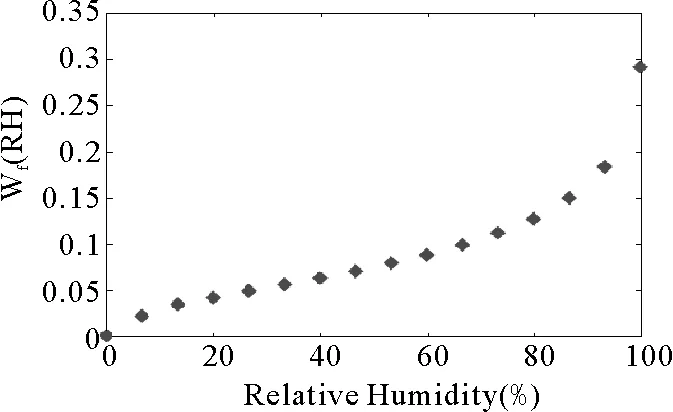
图3 实验测量粘胶纤维最大含水率[8]

在对纤维内水蒸汽体积浓度进行模拟时，同样需要对半径以及时间的偏微分方程进行边界条件与初始值的设定，如式(4)所示：

(4)

3 模型离散分析

本节采用利用有限差分法中的Crank-Nicolson模式进行方程离散，我们仍以一维的热传导方程为例，如式(5)所示：

(5)

采用Crank-Nicolson式进行离散时，前期的网格划分与显格式相同这里就不加以介绍，Crank-Nicolson格式如式(6)所示。

(6)

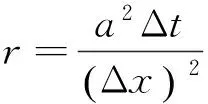
(7)

采用第n时间层的值计算第n+1的值时，我们需要转化为对角方程组进行求解，如式(8)所示。

(8)

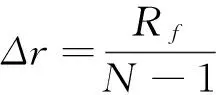
可转化为

(9)

其中i=2,…,N-1。

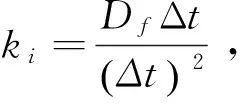
(10)

推出式(11)

(11)

然后将式转化为矩阵形式得：

(12)

(13)

按照上述矩阵关系式，进行等量代换，可得到式(14)：

(14)

同理可以获得i=N-1时等式，如式(15)：

(15)

通过对等式的整理，可得式(16)。

(16)

4 模拟结果

4.1 外界相对湿度对吸湿性能的模拟

结合上述的离散方程，采用Matlab编程语言进行数值求解。针对纤维内部水蒸气浓度的变化情况，如图4所示。首先根据图4所显示的模拟结果，在同一时刻，沿纤维半径方向，内部的水蒸气的体积浓度在不断增加。位置相同时，纤维内部的变化不大，外侧随着时间延长，纤维内部的水蒸气浓度增大，增大趋势随纤维半径的移动逐渐明显，但纤维内部整体的增加趋势是一个很缓慢的过程。

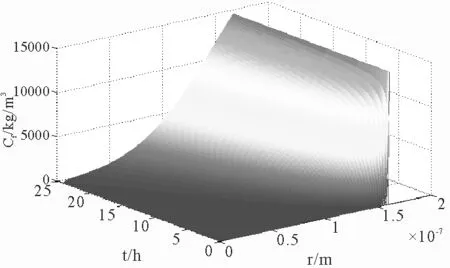
图4 纤维内部水蒸气浓度分布

除了纤维自身属性外，织物所处的外界环境也会对内部的水蒸气浓度产生影响，为探究环境的相对湿度对纤维吸湿性能的影响，本文假设外界环境的相对湿度分别为65%、75%、85%、90%时，分别对羊毛纤维内部水蒸气浓度以及体积浓度进行模拟。从图5，图6，图7和图8所显示的纤维内水蒸气的体积浓度随时间的变化曲线，同样可以看出：相对湿度越大，絮填料的吸湿速率会加快，在同一时刻，纤维内部的水蒸气浓度增大。并在最终测试点处达到峰值，峰值相应地的也随之增大。所以，外界相对湿度的增加，有利于提高纤维的吸湿性能。

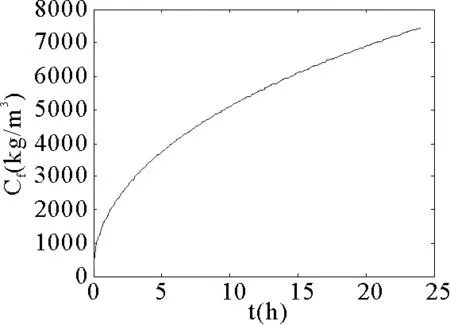
图5 RH=65%羊毛纤维内水蒸气浓度

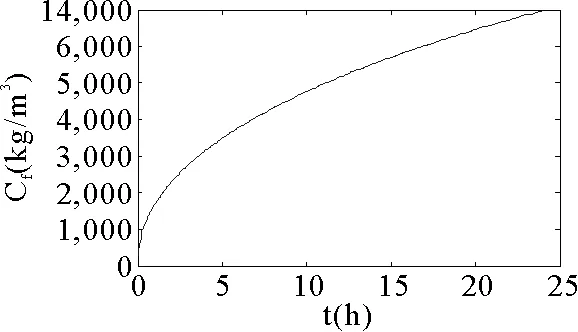
图6 RH=75%羊毛纤维内水蒸气浓度

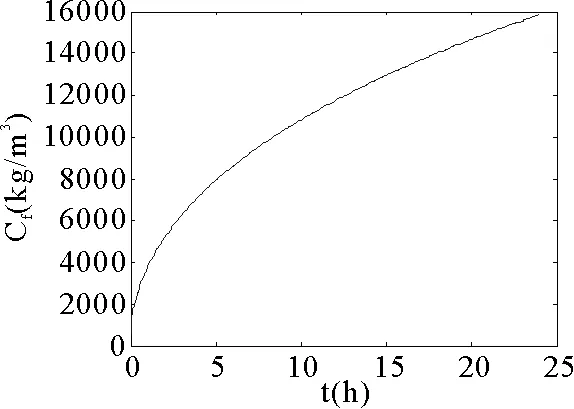
图7 RH=85%羊毛纤维内水蒸气浓度

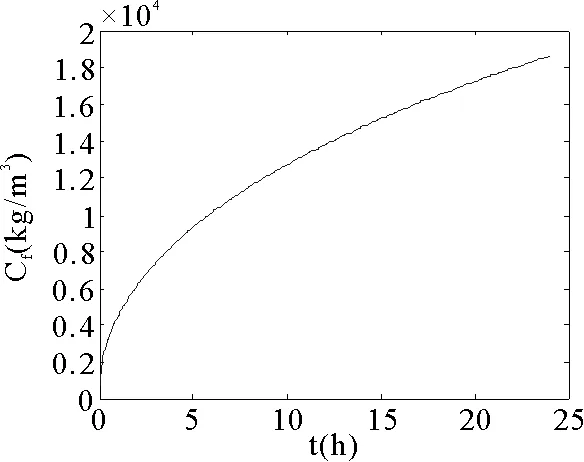
图8 RH=90%羊毛纤维内水蒸气浓度

4.2 填料纤维的物理属性对水蒸气浓度的影响

本节选取羊毛、羊绒二种絮填料，在外部环境相同的情况下，对两种纤维内部的水蒸气浓度进行数值模拟。图9，图10表示的是羊毛、羊绒两种纤维在时间t=24h时，在纤维直径方向水蒸气的体积浓度变化。图11，图12是对应的该两种纤维内部水蒸气浓度变化。通过这两组数值模拟的对比分析，相同的时间内，羊绒纤维内部的水蒸气浓度高于羊毛，羊绒的吸湿性能更好，并且在吸湿速度上也优于羊毛。所以在选取絮填料种类时，羊绒性能优于羊毛。针对本章的模拟，本文所采用的数据与文献[9]相同，通过与图11与图13的对比分析，结果吻合，纤维内部的水蒸气浓度的变化情况相符。所以该模型具有科学性。

图9 羊绒纤维内水蒸气体积浓度

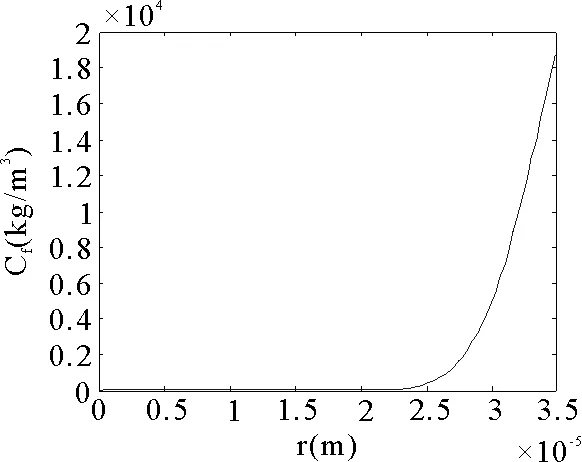
图10 羊毛纤维内水蒸气体积浓度

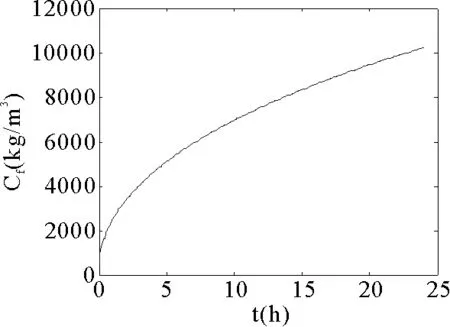
图11 羊绒纤维内水蒸气浓度

图12 羊毛纤维内水蒸气浓度

图13 羊绒纤维内水蒸气浓度[9]

5 结论

结合上述的模拟结果，针对填料吸湿性能的模型与实际结果相符，能够应用于实际的科研生产中去。同时通过模拟证明，同等条件下，羊绒纤维的吸湿性能优于羊毛纤维。另外，在保证其他参数相同的情况下，相对湿度越大，纤维的吸附性能越好，吸湿速率越快。

[1] 郭海燕.浅析吸湿性对纺织材料性能的影响[J].黑龙江纺织,2004,(2):7—8.

[2] 姚穆,周锦芳,黄淑珍，等.纺织材料学(第二版)[M].北京: 纺织工业出版社,1990.

[3] 王建君.纺织纤维水分测试方法研究与应用[D].长沙：湖南大学,2007.

[4] 陈天文,傅吉全,李伟哲，等.织物的吸湿及放湿性研究[J]. 北京服装学院学报(自然科学版),2005,(4):48—56.

[5] 刘凌杰,杜迎春.织物吸湿多分子层模型的模拟[J].纺织学报,2008,29(7):30—33.

[6] 李进,杜迎春.织物吸湿性能的研究及其动态模型[J].北京服装学院学报(自然科学版),2007,(3):24—30.

[7] 夏征农.大辞海化工轻工纺织卷[M].上海:上海辞书出版社,2009.

[8] 蒋达娅,肖井华,朱洪波.大学物理实验教程(第三版)[M].北京:北京邮电大学出版社,2011.

[9] Ye C, Huang H, Fan J, et al. Numerical study of heat and moisture transfer in textile materials by a finite volume method[J].Communications in Computational Physics, 2008, 4(4):929—948.

Simulation of Influencing Factor of Moisture Absorption for Winter Coat

CongShan,ZhuXiaoyu,WangYanwen

(Shanghai University of Engineering Science, Shanghai 201600, China)

According to the Fick law,an absorption model was established to explore influence of physical properties of fiber and the outside relative humidity on the absorption property, the finite difference method was used to discrete and the Matlab programming language was used to solve the numerical solution.

cashmere;absorption property;influencing factor; the model of absorption

2014-12-17

上海工程技术大学大学生创新项目(E1-0800-14-02353)

丛 杉(1973—)，女，吉林吉林人，副教授。

TS941.1

A

1009-3028(2015)03-0001-05