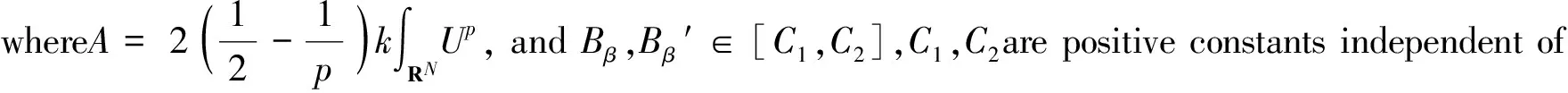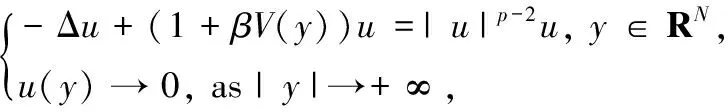Sign-changing solutions for a class of nonlinear Schrödinger equations
2015-03-21PENGShuangjieLONGWei
PENG Shuangjie, LONG Wei
(1.School of Mathematics and Statistics, Central China Normal University,Wuhan 430079;2.College of Mathematics and Information Science, Jiangxi Normal University, Nanchang 330022)
Sign-changing solutions for a class of nonlinear Schrödinger equations
PENG Shuangjie1*, LONG Wei1,2
(1.School of Mathematics and Statistics, Central China Normal University,Wuhan 430079;2.College of Mathematics and Information Science, Jiangxi Normal University, Nanchang 330022)
This paper is concerned with the existence of multiple non-radial sign-changing solutions for
multi-peak solutions; nonlinear Schrödinger equation; reduction method
1 Introduction
In this paper, we consider the following nonlinear Schrödinger problem
(1)
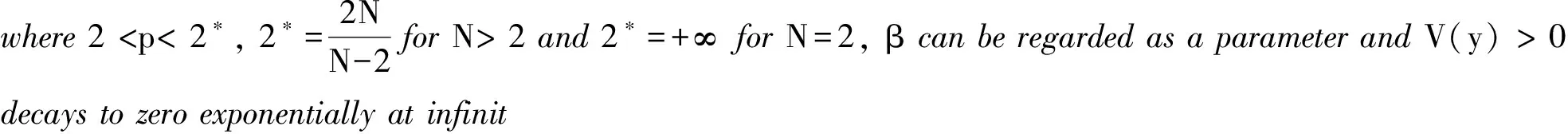
The problem (1) appears in many physical problems (see, e.g. literature [1-2]). For example, in some problems arising in nonlinear optics, in plasma physics and in condensed matter physics, the presence of many particles leads one to consider nonlinear terms which simulate the interaction effect among them. In recent years, many existences of ground states and higher energy solutions for (1) have been obtained. There are a lot of results in the literature, one can refer literature[3-11] and the references therein.
In literature[12], it has been proved that there are infinitely many solutions of (1), e.g. if 1+βV(y) ∈C(RN,R+) and 1+βV(y) →∞ as |y|→∞.Inthissituationtheexistenceofapositiveandanegativesolutioncanbefoundinliterature[9].Theseresultshavebeengeneralizedinliterature[13],andinliterature[14]theexistenceofasignchangingsolutionhasbeenobtained.Theresultsfromliterature[1]forDirichletproblemsonboundeddomainssuggestthat(1)shouldhaveanunboundedsequenceofsignchangingsolutions.Inliterature[15],theauthorsimproveontheresultfromliterature[14]abouttheexistenceofonesignchangingsolution.
Recently,inliterature[5],Lin,LiuandChenshowedthatifV(y) satisfies
(2)
thenasβ→ 0,equation(1)hasmultiplepositivesolutions.Inliterature[11],WeiandYanusedaconstructionargumenttoobtainaveryinterestingresult,whichsaysthatif
(3)
(thisisaspecialcaseofcondition(2)),thenforanyβfixed,problem(1)hasinfinitelymanynon-radialsignchangingsolutions.
Nowthereisaninterestingproblembasedonthefollowingcase
(4)
Inthispaper,wewillconsider(1)undertheassumption(4).Ouraimistoobtainmultiplesign-changingsolutionstoequation(1).
Forsimplicity,wesupposethatV(y)=V(|y|)satisfiesthefollowingdecayassumptionatinfinity,whichisaspecialcaseof(4):
(V):Thereareα∈R,α∈(0, 1],suchthat
V(r) ~rαe-αr, asr→+∞.
Ourmainresultsinthispapercanbestatedasfollows.
Theorem 1Suppose that (V) holds andk>1 is an integer. Then problem (1) has a non-radial sign-changing solution with exactlykmaximum points andkminimum points provided thatkandβsatisfy one of the following conditions:
whereβ*2andβ*2dependonα,kandN.
Remark 1In fact, our results are true for more general problems with more generalV(y).
Remark 2In assumption (V), ifα∈(1, 2),thenParts(ii)ofTheorems1arestilltrue,whichwillbeclarifiedinRemark4inSect.2later.
Ifweconsiderthefollowingsingularlyperturbedproblem:
-ε2Δu+V(y)u=|u|p-2u,u∈H1(RN),
(5)
whereε>0isasmallparameter,solutionsof(5)usuallyexhibitaconcentrationphenomenonasε→ 0+.Thatis,thesolutionsmayconcentrateatsomepointssuchatthecriticalpointsofV(y), for instance, literature[2, 6, 9, 16-21]. The solutions we obtain in Theorem 1 do not concentrate near any fixed point, and they have multiple bumps separated far apart with each bump resembling the shape of the solution of (6). Similar phenomenon was also observed in literature[4, 5, 11].
Before we close this introduction, let us outline the main idea in the proof of Theorem 1.
We will use the unique ground stateUof
(6)
tobuilduptheapproximatesolutionsfor(1).Itiswell-knownthatU(y)=U(|y|)isnondegenerate(seethedefinition(f2) in Remark 2) and satisfies
Let
∈RN,j=1, 2,…, 2k,
wherer> 0 is a large parameter, which will be determined later.
Define
Set
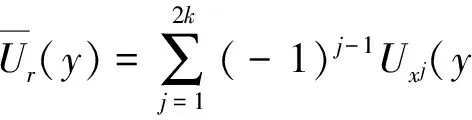
ToproveTheorem1,weonlyneedtoverifythefollowingresult:
Theorem 2If
Moreover,
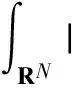
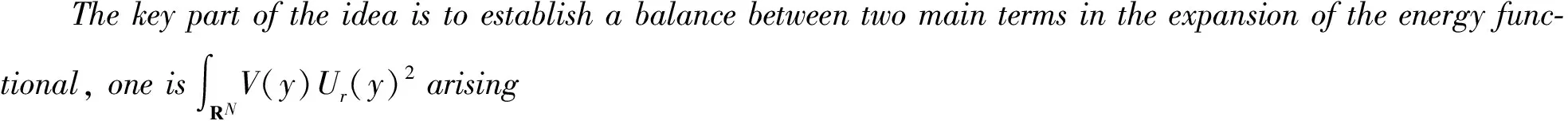
This paper is organized as follows. We will carry out a reduction procedure and study the reduced one dimensional problem to prove Theorem 2 in Sect.2. In Appendix, some basic estimates and an energy expansion for the functional corresponding to problem (1) will be established.
2 Reduction
Let
(7)
whereαistheconstantinexpansionforV, andδ∈(0, 1)isasmallconstant.
Define
ThenormofH1(RN)isdefinedasfollows:
‖u‖2=〈u,u〉,u∈H1(RN),
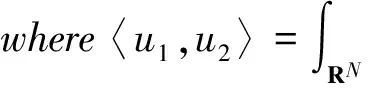
WedefinethefollowinglinearoperatorLonE, satisfying
(8)
Lemma 1There is a constantρ> 0suchthat
‖Lu‖≥ρ‖u‖, ∀u∈E,
providedthatoneofthefollowingconditionsholds:
‖Lun‖=o(1), ‖un‖=1.
Wehave
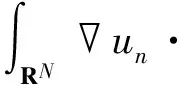
o(1)‖φ‖, ∀φ∈E.
(9)
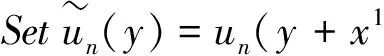
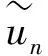
(10)
Now,weclaimthatusatisfies
-Δu+u-(p-1)Up-2u=0 in RN.
(11)
Indeed,weset
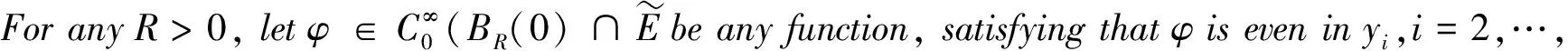
i.e.
Since
and
wefind
(12)
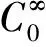
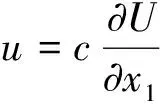
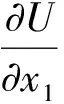
u=0.
Asaresult,
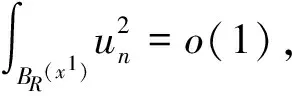
Thus,
providedthatRandnare large enough.
As a result, we get a contradiction.
Let
By a direct calculation, we have
where
and
We have the following estimates.
Lemma 2There is a constantC> 0 independent ofβsuch that
‖R′(ω)‖=O(‖ω‖min{2,p-1})
and
‖R″(ω)‖=O(‖ω‖min{1,p-2}).
ProofWe omit the details.
Lemma 3For a small T> 0, we can findC> 0independentofβsuchthat
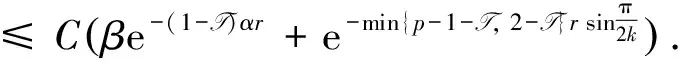
ProofUsing literature[22] Lemma 3.7, we have
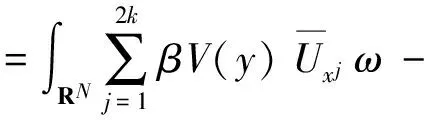
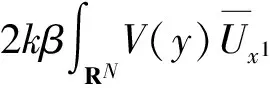
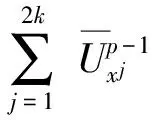
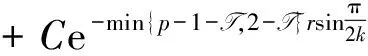
Hence
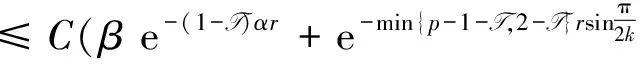
Proposition 1Under the conditions of Lemma 1, for anyr∈S,thereisauniqueω∈Esatisfying
J′(ω)|E=0.
(13)
Morover,
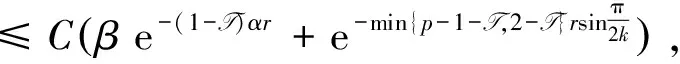
whereT is the same as that of Lemma 3.
ProofBy using Lemma 3,l(ω)isaboundedlinearfunctionalonE.WeknowbyReiszrepresentationtheoremthereisanl∈E,suchthat
l(ω)=〈l,ω〉.
So,findingacriticalpointforJ(ω)isequivalenttosolving
l+Lω+R′(ω)=0.
(14)
ByLemma1,Lis invertible. Thus, (14) is equivalent to
ω=A(ω)∶=-L-1(l+R′(ω)).
Set
whereT Now we verify thatAis a contraction fromSrtoSr.Indeed,wesee ‖A(ω)‖≤(‖l‖+‖R′(ω)‖)≤ ‖l‖+C‖ω‖min{2,p-1}≤ whichimpliesthatAmapsSrtoSr. On the other hand, for anyω1,ω2∈Sr, ‖A(ω1)-A(ω2)‖= ‖L-1R(ω1)-L-1R(ω2)‖≤ C‖R(ω1)-R(ω2)‖≤ C‖R′(θω1-(1-θ)ω2)‖‖ω1-ω2‖ ≤ C‖ω1+ω2‖‖ω1-ω2‖ ≤ Hence,Ais a contraction map inSrand the result follows from the contraction mapping theorem. Now, we are ready to prove Theorem 2. Letω=ωrbe obtained in Proposition 1, and define Proof of Theorem 2Since itfollowsfromPropositions1and2that (15) Define Weconsiderthefollowingmaximizationproblem Foranyk> 0satisfying wecancheckthatthefunction hasamaximumpoint and Bydirectcomputation,wededucethat Ontheotherhand,byβ< 0,wefind and forsomeδ0>0. isasolutionof(1). Weconsiderthefollowingminimizationproblem Foranyk> 0satisfying wefindthat hasaminimumpoint and Similarly,wededucethat Ontheotherhand,wesee and forsomeδ0 > 0. isasolutionof(1). Remark 3In assumption (V)(or(V′)), ifα∈(1, 2),thenParts(ii)ofTheorem2arestilltrue.Indeed,inthiscase,weshouldmodifytheproofofProposition1andobtainthefollowingestimateonl Hence,wehavethefollowingenergyexpansion NowproceedingaswehavedonetoproveTheorem2,wecancompletetheproof. Inthissection,wewillgivetheenergyexpansionfortheapproximatesolutions. Proposition 2There is a small constant T> 0, such that ProofOn the one hand, we know (16) Ontheotherhand,byliterature[22]Lemma3.7,weget (17) Combining(16),wehave [1] Besieris I M. Soltions in Randomly Inhomogeneous Media, Nonlinear Electromagenetics[M]. New York: Academic Press, 1980:87-116. [2] Byeon J, Oshita Y. Existence of multi-bump standing waves with a critical frequency for nonlinear Schrödinger equations[J]. Comm Partial Difierential Equations, 2004, 29: 1877-1904. [3] Ding Y, Tanaka K. Multiplicity of positive solutions of a nonlinear Schrödinger equation[J]. Manuscripta Math, 2003, 112: 109-135. [4] Lin L, Liu Z. Multi-bump solutions and multi-tower solutions for equations on RN[J]. J Funct Anal, 2009, 257:485-505. [5] Lin L, Liu Z, Chen S. Multi-bump solutions for a semilinear Schrödinger equation[J]. Indiana Univ Math J, 2009, 58:1659-1689. [6] Lin F, Ni W M, Wei J. On the number of interior peak solutions for a singularly perturbed Neumann problem[J]. Comm Pure Appl Math, 2007, 60:252-281. [7] Lions P L. The concentration-compactness principle in the calculus of variations. The locally compact case I[J]. Ann Inst H Poincar'e Anal Non Lin'eaire, 1984, 1:109-145. [8] Lions P L. The concentration-compactness principle in the calculus of variations. The locally compact case II[J]. Ann Inst H Poincar'e Anal Non Lin'eaire, 1984, 1:223-283. [9] Rabinowitz P H. On a class of nonlinear Schrödinger equations[J]. Z Angew Math Phys, 1992, 43:270-291. [10] Wei J, Yan S. New solutions for nonlinear Schrödinger equations with critical nonlinearity[J]. J Differential Equations, 2007, 237:446-472. [11] Wei J, Yan S. Infinite many positive solutions for the nonlinear Schrödinger equation in Rn[J]. Calc Var Partial Difierential Equations, 2010, 37: 423-439. [12] Bartsch T, Wang Z Q. Existence and multiplicity results for some superlinear elliptic problems on RN[J]. Comm Partial Difierential Equations, 1995,20:1725-1741. [13] Bartsch T, Pankov A, Wang Z Q. Nonlinear Schrödinger equations with steep potential well[J]. Comm Contemp Math, 2001, 4: 549-569. [14] Bartsch T, Wang Z Q. Sign changing solutions of nonlinear Schrödinger equations[J]. Topol Methods Nonlinear Anal, 1999, 13: 191-198. [15] Bartsch T, Liu L, Weth T. Tobias sign changing solutions of superlinear Schrödinger equations[J]. Comm Partial Difierential Equations, 2004, 29:1-2,25-42. [16] Cao D, Peng S. Multi-bump bound states of Schrödinger equations with a critical frequency[J]. Math Ann, 2006,336: 925-948. [17] D’Aprile T, Pistoia A. Existence, multiplicity and profile of sign-changing clustered solutions of a semiclassical nonlinear Schrödinger equation[J]. Ann Inst H Poincar'e Anal Non Lin'eaire, 2009, 26:1423-1451. [18] Floer A, Weinstein A. Nonspreading wave packets for the cubic Schrödinger equation with a bounded potential[J]. J Funct Anal, 1986, 69: 397-408. [19] Kang X, Wei J. On interacting bumps of semi-classical states of nonlinear Schrödinger equations[J]. Adv Difierential Equations, 2000, 5: 899-928. [20] Li Y Y. On a singularly perturbed elliptic equation[J]. Adv Difierential Equations, 1997, 2: 955-980. [21] Sato Y. Multi-peak positive solutions for nonlinear Schrödinger equations with critical frequency[J]. Calc Var Partial Difierential Equations, 2007, 29:365-395. [22] Ambrosetti A, Colorado E, Ruiz D. Multi-bump solitons to lineraly coupled systems of nonlinear Schrödinger eguations[J]. Calc Var Partial Differential Equations, 2007, 30: 85-112. 2015-04-16. The Fund from NSF of China(11125101);Program for Changjiang Scholars and Innovative Research Team in University(IRT13066). PENG Shuangjie(1968- ),male,professor,doctoral supervisor,majoring in nonlinear partial differential equations and functional analysis. 1000-1190(2015)05-0657-08 一类非线性Schrödinger方程的变号解 彭双阶1, 龙 薇1,2 (1.华中师范大学 数学与统计学学院, 武汉 430079; 2.江西师范大学 数学与信息科学学院, 南昌 330022) 研究了下述非线性Schrödinger方程非径向对称的变号解的存在性.其中是一个参数,V(y)>0为满足指数衰减的权函数.当β→-∞(或0-)时,对任意正整数k>1,构造了上述方程恰好有k个极大值点和k个极小值点的非径向对称的变号解. 多峰解; 非线性Schrödinger方程; 约化方法 O175.25;O175.29 A *E-mail: sjpeng@mail.cⓒnu.edu.cn.
3 Proof of the main results
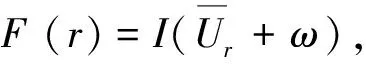

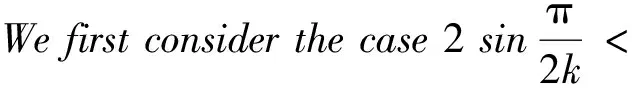
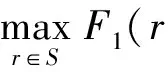
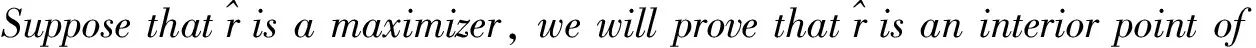
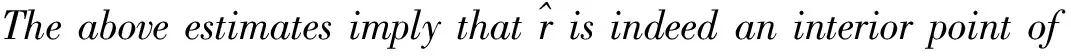
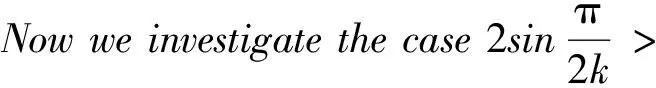
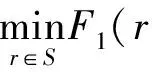

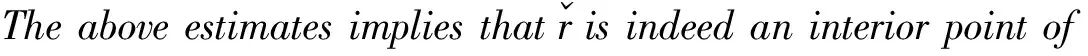
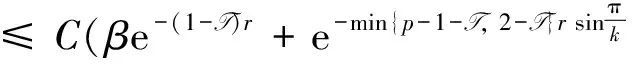
4 Energy expansion