Deformation Analysis on Shear-Bending of Ring-Shaped Piezoelectric Actuator

(康新)， (董帅), (何小元)

1. Department of Mechanical Engineering, Putian University, Putian 351100, P.R. China； 2. Department of Mechanics and Engineering Science, Nanjing University of Science and Technology, Nanjing 210094, P.R. China； 3. Institute of Mechanics, Southeast University, Nanjing 210018， P.R. China (Received 5 December 2014; revised 1 February 2015; accepted 30 July 2015)

Deformation Analysis on Shear-Bending of Ring-Shaped Piezoelectric Actuator

KangXin(康新)1,2*，DongShuai(董帅)2,3,HeXiaoyuan(何小元)3

1. Department of Mechanical Engineering, Putian University, Putian 351100, P.R. China； 2. Department of Mechanics and Engineering Science, Nanjing University of Science and Technology, Nanjing 210094, P.R. China； 3. Institute of Mechanics, Southeast University, Nanjing 210018， P.R. China (Received 5 December 2014; revised 1 February 2015; accepted 30 July 2015)

Deformation of a simple single piezoelectric actuator is usually quite small. A ring-shaped piezoelectric actuator with large piezoelectrically generated displacement was proposed. The thickness of the actuator was 1 mm, and the inner and outer diameters were 4 mm and 40 mm, respectively. The ring-shaped actuator was made of BiScO3-PbTiO3(BS-PT) ceramic and polarized in radial direction. An electric field was applied to thickness direction and a large shear-bending deformation emerged. Then Rayleigh-Ritz method and Bessel functions were adopted to analyze the shear-bending deformation. Results show that under an electric field of 7.5 kV/cm, the maximum displacement at the inner edge of the actuator reached 5.07 μm, which agreed well with the corresponding experimental results.

ring-shaped; piezoelectric actuator; shear-bending; Rayleigh-Ritz method

0 Introduction

Piezoelectric actuators have been widely used in camera modules, precision position control, adaptive optics, acoustics, pressure sensing and electricity generation[1-6], etc. Many researches have focused on piezoelectric actuators, in terms of structure theoretical analysis, optimum designs, and applications for intelligent structures. Dong et al.[7]presented analytical solutions to transverse deformation of a circular axisymmetric piezoelectric-metal composite unimorph actuator using thin plate and small bending theory of elasticity. Their approach predicted that there was an optimum thickness ratio between the piezoelectric and the metal layers, which led to a maximum deflection and load carrying capabilities. Fox et al.[8]devised a new analytical model for predicting the deflection of a circular plate with an annular piezoelectric actuator. They treated the plate and actuator as a mechanically over-constrained system and a structural mechanics approach was conducted to establish relevant equations. Lin[9]proposed an analytical model for deflections of a multi-layered circular annular piezoelectric actuator, subject to an applied voltage, reporting the effects on the transverse deflection of the laminate thickness, annular diameter, and residual stresses of the actuator. Lu et al.[10]advanced an exact solutions to a simply supported and functionally graded piezoelectric plate/laminate under cylindrical bending. Song et al.[11]discussed the stress and heat flow around a circular hole in thermopiezoelectric media with semi-permeable thermal boundary condition.

A multi-layer piezoelectric actuators are composed of piezoelectric, elastic and polymer layers, and epoxy resin is usually used to glue these components together. However, extreme environments, like high temperature, may greatly deteriorate the performance of piezoelectric actuators. Therefore, a simple single piezoelectric actuator may be more suitable for extreme conditions. Compared with multi-layer piezoelectric actuators, the single-layer ones have been seldom reported. Chen et al.[12]used both the finite element method and the experimental method to investigate deflection of a shear-bending mode actuator. However, the results of the two methods were distinctive and they did not present theoretical analysis.

An analytic approximate solution to the shear-bending deformation of the ring-shaped piezoelectric actuator[12]was presented by using Rayleigh-Ritz method and Bessel functions. The shear-bending deformation of the actuator was obtained and the corresponding results were discussed. The analysis results agreed well with the corresponding experimental results. The derived formulas will benefit the design and optimization of piezoelectric actuators.

1 Theoretical Analysis

Fig.1 shows a ring-shaped piezoelectric actuator which is simply supported at the external edge. The actuator was made of piezoelectric material (BS-PT ceramic). Ther-θplane was taken as the neutral plane of the actuator and the positivez-axis was pointed upward from the neutral plane. The actuator was polarized in the radial direction. When the plate was driven by external electric field along thickness direction, an out-of-plane deformation emerged due to shear-bending in the actuator.

Fig.1 Configuration of ring-shape piezoelectric actuator

1.1 Potential energy of the actuator

The actuator was 1 mm thick, and its inner and outer diameters were 4 mm and 40 mm, respectively. Hence the piezoelectric actuator can be considered as a thin plate, so we can assume

(1)

whereurepresents the displacement in cylindrical coordinate system, andw(r) the transverse deflection of the neutral plane of the actuator which can be expressed as

(2)

Considering the geometric equations of elasticity, we have

(3(a))

(3(b))

whereγθ r=0 andγz θ=0, because the polarization is along the radius direction, and the transverse deformation of the actuator presents axial symmetry. Also, we haveγz r≠0 which results in the shear-bending of the piezoelectric actuator. Considering the piezoelectric equation

(4)

whereSis the mechanical strain vector,sEthe mechanical compliant coefficient matrix at the constant electric fieldE,Tthe stress vector,Ethe electric field vector, anddtthe transpose matrix of the piezoelectric coefficient．The expansion expressions of the above vectors are

According to the fourth and the sixth equations of Eq.(4), we haveτθ r=0 andτz θ=0. Also, since the actuator can be considered as a thin plate, we can assumeσz=0. Considering the second and the third equations of Eq.(4), we can obtain

(5)

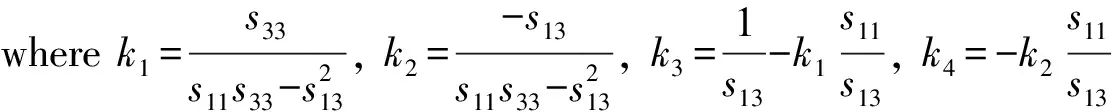
From the first equations of Eq.(4) and Eq.(5), we have

(6)

whereξ1=s12k1+s13k3,ξ2=s13k4+s12k2, and then we can obtain

(7)

wheref(r) is an arbitrary function. Considering Eq.(2), we obtainf(r)=w(r). Substituting the above equation into Eq. (7), and considering Eqs.(3), we can obtain

(8)

Considering the fifth equation of Eq.(4), we have

(9)

(10)

(11)

wherevis the integral element andΩthe whole region of the configuration regarding to the density of electric potential energy of the actuator, we can obtain

(12)

(13)

whereεTisthedielectricconstantmatrixunderconstantstressfield.Similarly,theelectricpotentialenergycanbeobtainedbyintegrationas

(14)

The total energy of the actuator is equal to the sum of the strain energy and the electric potential energy

(15)

1.2 Shape function of transverse deformation

Assume the shape function of the shear-bending deformation for the ring-shaped piezoelectric actuator is

(16)

(17)

(18)

(19)

whereJ2is the second-order Bessel function. According to Rayleigh-Ritz method, we have

(20)

Then we can obtainn-variable simple equations. By solving these simple equations we can obtain coefficientscnin Eq.(16), and then the maximum value of the transverse displacement of the actuator can be obtained accordingly.

2 Results and Discussions

The material properties for BS-PT ceramics are presented in Table 1.

Table 1 Material property of BS-PT ceramics

MATLAB was adopted to calculate the actuator shear-bending deformation. When the applied voltage reached 750 V, the out-of-plane displacement of the actuator was obtained (Fig.2). Fig.2 shows that the maximum of the transverse deformation is 5.074 3 μm, occurring at the inner edge of the actuator, and 11—14 times that of a single layer ceramic with the same thickness.

Fig.3 shows the relationship between the diameter ratio and the displacement at the actuator inner edge. We can see that the deformation results from the shear force decreases when the ratio of the inner to the outer diameter (a/b) increases. The results at ratio of 0.1 is shown in Fig.3, where (X,Y) is the coordinate of the black square point.

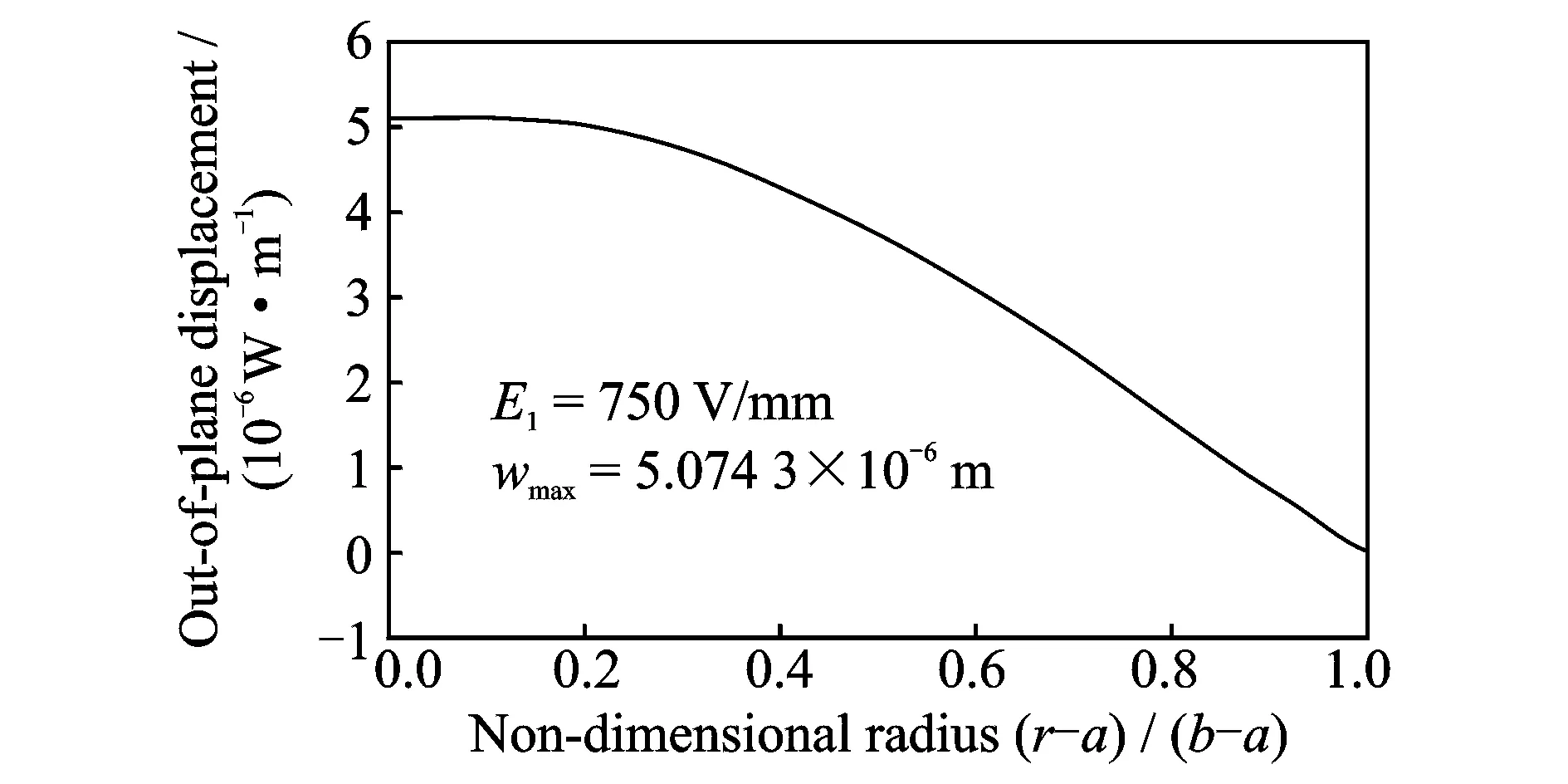
Fig.2 The calculated deformation using the proposed method

Fig.3 Relationship between diameter ratio and displacement

Chen et al.[12]have measured the displacement of the ring-shaped actuator at different temperatures with electric field applied. Fig.4 shows the sample of the actuator considered in this paper, and the corresponding experimental setup is illustrated in Fig.5. The actuator was placed in a thermal chamber，and was simply supported by a ring at the outer margin. A preload was applied through a compressive spring at the center of the actuator in order to obtain stable experimental data. The measurement results at 25 ℃ under a load of 2.5 N and an applied triangular waveform of electric voltage at 1 Hz (corresponding to an electric field of ±7.5 kV/cm) are shown in Fig.6. It can be seen that the measured amplitude of the ring-shaped actuator was about 4.5 μm at room temperature. The error between the proposed analysis results and the experimental results is 0.574 3 μm which may be attributed to the material parameters of the actuator.

Fig.4 Sample of the actuator

Fig.5 Experimental setup for displacement measurement

Fig.6 Test results for the transverse deformation

ANSYS finite element method (FEM) was used to simulate the corresponding deformation of the actuator. The simulated displacement at the center of the ring-shape actuator without a load under an applied electric field of 7.5 kV/cm was about 6 μm[12]which demonstrates that the proposed analysis results are superior to the FEM results.

3 Conclusions

The shear-bending deformation mechanism of a BS-PT ceramic ring-shaped piezoelectric actuator under an applied electric field was analyzed using Rayleigh-Ritz method. The maximum displacement under electric field of 7.5 kV/cm is calculated as 5.074 3 μm which agreed well with corresponding experimental results. The maximum displacement of the proposed actuator was about 11—14 times that of a single layer ceramic with the same thickness. The proposed method is effective and precise for analysis of ring-shaped piezoelectric actuators.

Acknowledgement

This work was supported by the National Natural Science Foundation of China (No.11172138).

[1] Lai L K, Tsai C L, Liu T S. Design of compact linear electromagnetic actuator for auto-focusing in phone camera[J]. IEEE Transaction on Magnetic, 2011, 47(12): 4740.

[2] Luo Q, Tong L. High precision shape control of smart plates using orthotropic piezoelectric actuators[J]. Finite Elem Anal Des, 2006, 42 (11): 1009-1020.

[3] Dong S X. Review on piezoelectric, ultrasonic, and magnetoelectric actuators[J]. Journal of Advanced Dielectrics, 2012, 2(1): 1230001-1230018.

[4] Shintaku H, Nakagawa T, Kitagawa D, et al. Development of piezoelectric acoustic sensor with frequency selectivity for artificial cochlea[J]. Sensors and Actuators A: Phys 2010, 158(2): 183-192.

[5] Olfatnia M, Xu T, Miao J M, et al. Piezoelectric circular microdiaphragm based pressure sensors[J]. Sensors and Actuators A: Phys, 2010, 163 (1): 32-36.

[6] Liu Xiangjian, Chen Renwen. Influence of materials and shape parameters on electricity generation by rainbow shape piezoelectric transducer[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(2): 198-204. (in Chinese)

[7] Dong S X, Uchino K, Li L T, et al. Analytical solutions for the transverse deflection of a piezoelectric circular axisymmetric unimorph actuator[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2007, 54(6): 1240-1249.

[8] Fox C H J, Chen X, McWilliam S. Analysis of the deflection of a circular plate with an annular piezoelectric actuator[J]. Sensors and Actuators A: Phys, 2007, 133: 180-194.

[9] Lin S I E. The theoretical and experimental studies of a circular multi-layered annular piezoelectric actuator[J]. Sensors and Actuators A: Phys, 2011, 165(2): 280-287.

[10]Lu P, Lee H P, Lu C. An exact solution for functionally graded piezoelectric laminates in cylindrical bending[J]. International Journal of Mechanical Sciences, 2005, 47(3): 437-458.

[11]Song Haopeng, Hu Wei, Gao Cunfa. Problem of circular hole in thermopiezoelectric media with semi-permeable thermal boundary condition[J]. Transactions of Nanjing University of Aeronautics and Astronautic, 2014,31(2): 162-168.

[12]Chen J G, Li X T, Liu G X, et al. A shear-bending mode high temperature piezoelectric actuator[J]. Applied Physics Letters, 2012, 101(1): 012909.

(Executive Editor： Zhang Bei)

TM382; TN384 Document code:A Article ID:1005-1120(2015)06-0585-06

*Corresponding author: Kang Xin, Professor, E-mail: ckkang@njust.edu.cn.

How to cite this article: Kang Xin， Dong Shuai, He Xiaoyuan. Deformation analysis on shear-bending of ring-shaped piezoelectric actuator [J]. Trans. Nanjing U. Aero. Astro., 2015,32(6):585-590. http://dx.doi.org/10.16356/j.1005-1120.2015.06.585