一种三维正交方位各向异性介质岩石物理建模及弹性波正演模拟方法

李雨生 吴国忱

（山东青岛266580中国石油大学（华东）地球科学与技术学院）



一种三维正交方位各向异性介质岩石物理建模及弹性波正演模拟方法

（山东青岛266580中国石油大学（华东）地球科学与技术学院）

通过线性滑动理论和岩石物理等效理论， 将两组正交直立裂隙介质等效为一种正交方位各向异性介质进行三维岩石物理建模， 通过高阶交错网格有限差分求解弹性波动方程模拟地震波在该种介质中的传播过程． 在建模过程中改变物性参数， 分析不同裂隙密度条件下的炮集和波场特征， 以及正交各向异性的方位特征． 研究结果表明， 各向异性强度随裂隙密度等物性增大而增强， 而且这些特征在共炮点道集和波场中均有所体现．

正交方位各向异性 裂隙介质 Hudson理论 线性滑动理论 交错网格有限差分

引言

地球介质广泛存在波动各向异性， 地震各向异性主要表现在地震波传播速度是传播方向的函数、 体波间相互耦合、 横波发生分裂等（吴国忱， 2006）． 近几十年地震各向异性研究取得了很大的进展， 特别是Backus（1962）研究表明周期性薄互层可引起视各向异性， Crampin证实了裂隙诱导各向异性和横波分裂的存在， 并于1987年提出了广泛扩容各向异性（extensive dilatancy anisotropy， 简写为EDA）模型（Crampin， 1978， 1981， 1987）． 裂隙介质不仅是油气运移的重要通道， 还是重要的油气存储空间， 因此在油气勘探领域越来越受到重视（金抒辛， 何樵登， 2005； 吴国忱， 秦海旭， 2014）． 裂隙中弹性波在传播过程中呈现出方位各向异性特征． 具有方位各向异性特征的介质包括HTI （horizontal transverse isotropic）介质、 正交各向异性介质和单斜各向异性介质等， 本文着重将两组正交直立裂隙等效为一种正交各向异性介质． 虽然早在20世纪80年代初， Crampin等（1980）就提出双平面裂隙系统， 但后续的相关研究只侧重于在薄互层背景上发育有垂直定向排列的裂隙（Schoenberg， Hilbig, 1997； 张文生， 宋海滨， 2001； 何燕， 2008）．

线性滑动理论（Schoenberg， 1980； Coates， Schoenberg， 1995； Schoenberg， Muir， 1989； Schoenberg， Sayers， 1995; Bakulinetal， 2000a， b， c）将裂隙看作无限的、 很薄的且具有很强屈服性的层面， 或将其看作具有线性滑动边界条件的柔性平面． 在此基础上， 可将裂隙模型等效为正交各向异性来进行岩石物理建模， 为地震波数值模拟提供速度模型．

地震波正演模拟是模拟地震波在地球介质中的传播过程， 并研究地震波的传播特性与地球介质参数的关系（孙成禹， 2007）， 波动方程数值模拟是正演模拟的一种非常重要的方法． 数值模拟是通过数值计算达到对实际地震剖面的最优逼近， 是应用数值方法研究地下储层地震反射特征的基础工具． 常见的波动方程数值解法包括有限差分法和有限元法等． 有限差分法是将波动方程中的介质参数和波场函数离散化， 以差分算子代替微分算子， 在有限精度内对地震波传播问题进行模拟． Virieux（1987）给出了波动方程一阶速度-应力方程并用交错网格模拟地震波在非均匀介质中的传播过程． 交错网格差分法相对规则网格差分法, 其网格频散显著减小， 精度明显提高， 而且可以取较大的空间步长， 提高计算效率（董良国等， 2000）． 利用有限差分法模拟地震波的传播过程主要有3个需要注意的问题， 即边界条件处理、 频散压制和差分稳定性条件． 其中边界条件的处理本文采用最佳匹配层（perfectly matched layer， 简写为PML）法． 该方法由Berenger（1994）针对电磁波传播情况提出， Collino和Tsogka（2001）将其应用于各向异性介质地震波数值模拟． Boris和Book（1973）将求解流体动力学问题时的通量校正传输方法应用于声波方程求解， 实现了声波方程差分计算中数值频散的有效压制．

本文拟基于线性滑动理论结合Hudson理论， 将两组垂直正交裂隙介质等效为正交方位各向异性介质， 利用多组物性参数， 计算得到不同裂隙密度下的弹性参数， 并以此来建立三维模型． 通过有限差分正演模拟弹性波在这些介质中的传播过程， 分析不同物性条件下共炮点道集和波场的特征及其各向异性的方位特征．

1 基于线性滑动理论结合Hudson理论的岩石物理建模

Schoenberg（1980）指出， 可以忽略裂隙的形状而将其看作满足线性滑动边界条件的柔性平面． 所谓线性滑动， 是指两个弹性固体接触面上的应变是不连续的， 但引起应变的应力在接触面上是连续的， 且应力与应变成线性关系．

正交裂隙是实际存在的一种重要正交介质， 是各向同性介质背景或VTI（vertical transverse isotropic）介质背景中两组正交的直立裂隙． 图1给出了上述正交介质的实际发育情况及相应模型. 可以看出， 该正交介质由两组正交的直立裂隙组成．

图1 正交介质模型， 图中红线和虚线均表示裂隙

Bakulin等（2000a, b, c）结合线性滑动理论和Hudson（1981）理论给出了不同裂隙介质弹性矩阵的计算方法. 各向同性介质背景下的两组正交直立裂隙的弹性系数矩阵可表示为（Bakulinetal, 2000b）：

（1）

其中，

（2）

（3）

l1=1-ΔN1，l2=1-rΔN1，l3=1-r2ΔN1，l4=4r2g2ΔN1ΔN2，

m1=1-ΔN2，m2=1-rΔN2，m3=1-r2ΔN2，

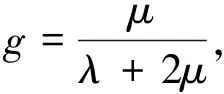
（4）

式中：λ和μ分别为裂隙所在背景介质的拉梅参数，ΔN和ΔT分别为法向柔度和切向柔度， 其大小与裂隙充填物有关， 具体表达式详见Hudson（1981）.

2 三维正交方位各向异性介质弹性波方程及高阶交错网格有限差分正演模拟

2.1 三维正交介质弹性波一阶速度-应力方程

根据本构方程， 几何方程和运动微分方程推导出三维正交介质一阶速度-应力方程为

（5）

（6）

式中,v为速度，τ为应力，c为刚度矩阵元素，ρ为密度，F为震源项.

2.2 三维正交介质弹性波交错网格有限差分正演模拟

利用泰勒展开得到式（5）和式（6）的时间和空间差分形式：

时间1阶差分：

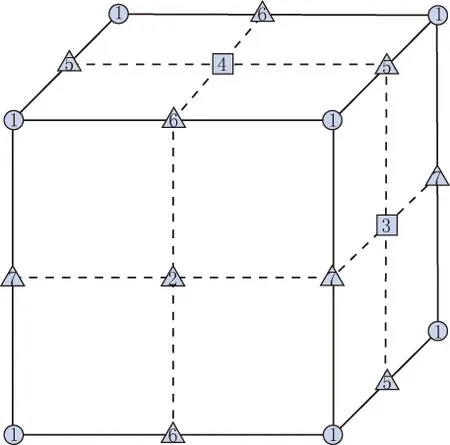
图2 变量定义的网格

（7）

空间2N阶差分：

）.

（8）

交错网格变量在网格上的定义形式与常规网格不同． 图2给出了变量定义的网格， 7种网格点上定义不同的变量， 其具体定义形式列于表1.

2.3 正演模拟过程中的问题

表1 标准交错网格中弹性波场分量和弹性参数的空间位置 Table 1 Position of elastic wavefield components and elastic parameters in standard staggered grid

3个问题， 即边界条件处理， 频散压制和差分稳定性条件．

鉴于只能在有限区域内进行波动方程求解， 因此在区域边界处会产生强烈的人为边界反射. 该边界反射对研究地震波的传播没有意义且会干扰对正常波场的认识， 故相关人员近些年一直致力于消除边界反射的研究， 产生了许多边界条件， 本文采用PML边界条件．

为避免直接进行傅里叶反变换需要在时间域作褶积， 首先对波场进行分解， 将不同波场分量分别沿x、y、z轴方向分裂， 并假定体力为0， 得到

（9）

这里以

（10）

为例， 推导其PML边界方程. 根据复数坐标变换规律

（11）

可得空间方向微分变换关系

（12）

式中dn（n）为不同方向的衰减系数. 对式（10）进行傅里叶变换得

英格曼神甫的恳求得到了少佐的批准。他的部队在寒冷中静默地多候了二十分钟。英格曼给的理由是说得过去的：唱诗礼服很久没被穿过，有的需要钉钮扣，有的需要缝补、熨烫。士兵们站在围墙外，一个挨一个，刺刀直指前方。多二十分钟就多二十分钟吧，好东西是值得等待的。日本人是最讲究仪式的。一盘河豚上桌，都装点成艺术品，何况美味的处女。

（13）

将上式代入式（12）并在时间和空间方向进行泰勒展开， 化简可得

（14）

此则为式（10）的PML边界表达式. 类似可推导出三维正交介质PML表达式为

（15a）

（15b）

（15c）

（16a）

（16b）

（16c）

（16d）

（16e）

（16f）

图3为震源位于一均匀立方正交介质模型中心激发所得到的正演波场. 图3a中纵波经过边界反射回来的能量强于横波， 对波场分析造成严重干扰； 图3b中纵波传到边界处被消除干净， 相比图3a中横波能量较强． 可以看出PML边界条件消除人工边界的效果明显． 这里注意， 由于u，v，w等3个波场分量上均有一个界面垂直于纵波传播方向而导致截面上纵波很弱， 故这里每个波场分量只取两个截面．

图3 加最佳匹配层条件前（a）、 后（b）的三维正交各向异性介质波场

3 模型试算

3.1 均匀模型正交介质波场分析

利用基于线性滑动理论结合Hudson理论求取的对应不同裂隙密度的弹性系数矩阵建立两组正交直立裂隙的正交介质均匀模型． 模型大小均为3.0 km×3.0 km×3.0 km； 混合密度ρ=2.625×103kg/m3； 拉梅参数分别为λ1=16.3 GPa,μ1=7.0 GPa，λ2=7.7 GPa,μ2=44.0 GPa； 背景介质为砂岩和泥岩各占一半， 干燥裂隙， 裂隙纵横比为0.01， 裂隙密度为0.04． 在模型中心采用等能量震源激发， 时间网格dt=1 ms， 空间网格dx=dy=dz=10 m， 分别在过震源的3个垂面截取三分量0.2 s时的波场快照进行对比．

图4给出了两组正交直立裂隙正交介质的三维波场． 结合图1可以看出， 由于裂隙的存在， 平行于裂隙的方向为各向同性面， 其波速大于垂直裂隙方向．xoy面内波场传播受到两套相互正交的裂隙影响， 裂隙密度相等， 纵波波场近似成正方形；xoz面和yoz面分别受单套裂隙影响， 纵波波场近似成矩形， 垂直裂隙方向边长小于平行裂隙方向． 所有截面内横波分裂严重， 说明当裂隙密度达到0.1时介质各向异性较强．

图4 裂隙密度为0.1时的三维正交各向异性介质波场

3.2 裂隙密度对波场的影响

通过改变裂隙密度建立4种裂隙模型， 裂隙密度分别给定为0.02， 0.04， 0.06和0.1． 图5为正交介质波场随裂隙密度的变化情况． 可以看到， 在裂隙密度从左到右依次增大的过程中， 波场传播速度减小， 纵波波场形状由圆形逐步转化为类似方形． 其中u分量的xoy面波场受到两组裂隙的影响， 当裂隙密度增大为0.1时其近似成正方形；u分量xoz面波场受到单组裂隙的影响， 当裂隙密度增大为0.1时其近似成矩形． 从横波波场变化可以看出， 随着裂隙密度增大， 介质各向异性增强， 其横波分裂现象加重， 三叉区现象变得尤为明显．

图5 正交各向异性介质波场随裂隙密度ρF变化

图6 层状正交介质模型

3.3 层状模型分析

为分析不同裂隙密度对道集的影响， 我们建立多组三维正交介质模型， 如图6所示． 图中黄色为各向同性层, 棕色为裂隙层， 大小为3.0 km×3.0 km×1.5 km， 时间网格dt=1 ms， 空间网格dx=dy=dz=10 m. 这些模型均为3层： 第一层和第三层为各向同性介质， 给定纵、 横波速度分别为4.0 km/s和2.5 km/s； 中间层为裂隙密度分别为0.02， 0.04， 0.06和0.1的正交介质.

首先分析裂隙密度为0.02时的共炮点道集和波场． 图7为3个波场分量0°（沿x轴方向）测线的共炮点道集． 切除直达波后， 可以明显看出两个分界面的反射纵波和反射横波．

炮点放置于模型顶面中心处， 过炮点截取u分量3个相互垂直面上0.2 s时的波场, 如图8所示. 由于截取传播时间的原因， 在波场上我们只能区分一个界面的透射纵横波和反射纵横波．

分别抽取与x轴方向成不同夹角的u分量道集, 绘制成图9， 方位角分别为0°， 30°， 45°， 60°， 90°， 120°， 135°， 150°和180°等9个方位道集． 可以看出， 以90°为中心左右对称（两组裂隙密度相同）， 红色椭圆标出了不同方位角反射旅行时的变化， 其中45°和135°时道集上反射波旅行时最大， 这与其同时受到两组裂隙的影响有关．

图7 裂隙密度为0.02时层状模型u分量正交介质共炮点道集

图8 裂隙密度为0.02时层状模型正交介质0.5 s时的波场

图9 裂隙密度为0.02时层状模型正交介质u分量不同方位共炮点道集

不同裂隙密度下层状模型u分量波场如图10所示. 可以看出, 随着裂隙密度的增大, 红色椭圆中标出的裂隙层底界面反射波旅行时的增大， 横波分裂现象更突出， 说明裂隙对波场传播和介质各向异性性质有较大影响．

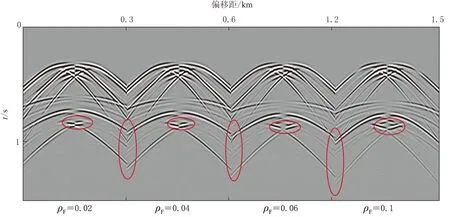
图10 不同裂隙密度ρF下层状模型正交介质u分量共炮点道集

4 讨论与结论

本文利用线性滑动理论结合Hudson理论将两组正交直立裂隙介质等效为一种新的正交方位各向异性， 并用该方法进行岩石物理建模， 通过改变物性参数得到多组弹性参数． 在此基础上， 推导了该正交介质的弹性波动方程， 并采用有限差分法进行求解． 正演过程中使用PML边界条件处理人为边界反射． 最后通过分析正演波场和共炮点道集来模拟地震波在该介质中的传播过程， 分析裂隙密度等物性条件对波场和道集的影响以及方位各向异性特征．

本文结果表明， 裂隙密度的增大会使正交裂隙介质的各向异性强度明显增强， 从而导致垂直和平行裂隙方向上的纵波速度差别增大， 横波变得更加复杂， 分裂严重． 通过对层状模型正演模拟， 在共炮点道集和正演波场中可以清晰地分辨出直达波和反射波中的纵波和分裂后的横波． 抽取不用方位测线记录的共炮点道集， 通过比较反射波旅行时来描述介质的方位特征， 结果表明不同方位上地震波传播过程不尽相同， 这与介质中发育的两组直立正交裂隙不无关联．

董良国， 马在田， 曹景忠， 王华忠， 耿建华， 雷冰， 许世勇. 2000. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报， 43（3）: 411--419.

Dong L G， Ma Z T， Cao J Z， Wang H Z， Geng J H， Lei B， Xu S Y. 2000. A staggered-grid high-order difference method of one-order elastic wave equation[J].ChineseJournalofGeophysics， 43（3）: 411--419 （in Chinese）.

何燕. 2008. 正交各向异性弹性波高阶有限差分正演模拟研究[D]. 东营: 中国石油大学（华东）地球资源与信息学院: 4.

He Y. 2008.High-OrderFinite-DifferenceForwardModelingofElastic-WaveinOrthorhombicAnisotropicMedia[D]. Dongying: College of Georesources and Information， China University of Petroleum: 4 （in Chinese）.

金抒辛， 何樵登. 2005. 泥岩裂隙的正演模拟方法研究[J]. 石油物探， 44（2）: 119--123.

Jin S X， He Q D. 2005. The forward modeling of mudstone fractures[J].GeophysicalProspectingofPetroleum， 44（2）: 119--123 （in Chinese）.

孙成禹. 2007. 地震波理论与方法[M]． 东营： 中国石油大学出版社: 211.

Sun C Y.2007.TheoryandMethodsofSeismicWaves[M]. Dongying: China University of Petroleum Press: 211 （in Chinese）.

吴国忱. 2006. 各向异性介质地震波传播与成像[M]． 东营： 中国石油大学出版社: 1.

Wu G C. 2006.SeismicWavesPropagationandImaginginAnisotropicMedium[M]. Dongying: China University of Petroleum Press: 1 （in Chinese）.

吴国忱， 秦海旭. 2014. 裂缝介质旋转交错网格正演模拟[J]. 地震学报， 36（6）: 1075--1088.

Wu G C， Qin H X. 2014. Rotated staggering grid forward modeling in fractured medium[J].ActaSeismologicaSinica， 36（6）: 1075--1088 （in Chinese）.

张文生， 宋海滨. 2001. 三维正交各向异性介质三分量高精度有限差分正演模拟[J]. 石油地球物理勘探， 36（4）: 422--432

Zhang W S， Song H B. 2001. Finite-difference forward modeling of three component records with high precision in 3-D orthorhombic anisotropic media[J].OilGeophysicalProspecting， 36（4）: 422--432 （in Chinese）.

Backus G E. 1962. Long-wave elastic anisotropy produced by horizontal layering[J].JGeophysRes， 67（6）: 4427--4440.

Bakulin A， Grechka V， Tsvankin L. 2000a. Estimation of fracture parameters from reflection seismic data， part 1: HTI model due to a single fracture set[J].Geophysics， 65（6）: 1788--1802.

Bakulin A， Grechka V， Tsvankin L. 2000b. Estimation of fracture parameters from reflection seismic data， part 2: Fracture models with orthorhombic symmetry[J].Geophysics， 65（6）: 1803--1817.

Bakulin A， Grechka V， Tsvankin L. 2000c. Estimation of fracture parameters from reflection seismic data， part 3: Fracture models with monoclinic symmetry[J].Geophysics， 65（6）: 1818--1830.

Berenger J P. 1994. A perfectly matched layer for absorption of electromagnetic waves[J].JComputPhys， 114（2）: 185--200.

Boris J P， Book D L. 1973. Flux-corrected transport. I: SHASTA， a fluid transport algorithm that works[J].JComputPhys， 11（1）: 38--69.

Coates R T， Schoenberg M. 1995. Finite-difference modeling of faults and fractures[J].Geophysics， 60（5）: 1514--1526.

Collino F， Tsogka C. 2001. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J].Geophysics， 66（1）: 294--307.

Crampin S. 1978. Seismic-wave propagation through a cracked solid: Polarization as a possible dilatancy diagnostic[J].GeophysJInt， 53（3）: 467--496.

Crampin S， McGonigle R， Bamford D. 1980. Estimating crack parameters from observations of P-wave velocity anisotropy[J].Geophysics， 45（3）: 345--360.

Crampin S. 1981. A review of wave motion in anisotropic and cracked elastic-media[J].WaveMotion， 3（4）: 343--391.

Crampin S. 1987. Geological and industrial implications of extensive-dilatancy anisotropy[J].Nature， 328（6130）: 491--496.

Hudson J A. 1981. Wave speeds and attenuation of elastic waves in material containing cracks[J].GeophysJInt， 64（1）: 133--150.

Schoenberg M. 1980. Elastic wave behavior across linear slip interfaces[J].JAcoustSocAm， 68（5）: 1516--1521.

Schoenberg M， Muir F. 1989. A calculus for finely layered anisotropic media[J].Geophysics， 54（5）: 581--589.

Schoenberg M， Sayers C. 1995. Seismic anisotropy of fractured rock[J].Geophysics， 60（1）: 204--221.

Schoenberg M， Hilbig K. 1997. Orthorhombic media: Modeling elastic wave behavior in a vertically fractured earth[J].Geophysics， 62（6）: 1954--1974.

Virieux J. 1987. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method[J].Geophy-sics， 51（4）: 889--901.

Rock physics modeling and elastic wave forward modeling methods in a three-dimensional azimuthally anisotropic medium of orthorhombic symmetry

（SchoolofGeosciences,ChinaUniversityofPetroleum，ShandongQingdao266580,China）

In this paper， by rock physical equivalent theory and linear slip theory， two sets of orthorhombic fractures are equivalent to a new three-dimensional azimuthally anisotropic medium of orthorhombic symmetry for rock physical modeling. And then elastic wave equations are solved to simulate the propagation process in this medium by high-order staggered-grid finite-difference method. During the process of modeling， with the variation of physical parameters， we analyze CSP （common shot points） sets and the wave field characteristics on the conditions of different fracture densities， as well as azimuthal characteristics of orthorhombic anisotropy. The research results show that the anisotropic strengths enhance with fracture density increasing， which is reflected in the CSP sets and forwarding wavefield.

azimuthal anisotropy of orthorhombic symmetry; fracture medium; Hudson theory; linear slip theory; staggered-grid finite-difference

10.11939/jass.2015.04.013.

国家973项目（2013CB228604）资助.

2014-11-19收到初稿， 2015-04-27决定采用修改稿.

e-mail: 15610031211@163.com

4.013

P315.3+1

A

李雨生, 吴国忱. 2015. 一种三维正交方位各向异性介质岩石物理建模及弹性波正演模拟方法. 地震学报, 37（4）: 678--689.

Li Y S, Wu G C. 2015. Rock physics modeling and elastic wave forward modeling methods in a three-dimensional azimuthally anisotropic medium of orthorhombic symmetry.ActaSeismologicaSinica, 37（4）: 678--689.

doi:10.11939/jass.2015.04.013.