求解随机二阶锥线性互补问题的期望残差最小化方法

张宏伟，贾 红，陈 爽，庞丽萍

（大连理工大学 数学科学学院，辽宁 大连 116024）

0 引 言

Rn中的二阶锥，也称冰淇淋锥或洛伦兹锥，定义为其中为欧式范数.若n＝1，则Kn即为非负象限R＋.一般对包含二阶锥（SOCs）的互补问题比较感兴趣.二阶锥互补问题作为线性互补问题的扩展，在线性问题、二次规划问题及一些网络均衡问题中均具有广泛的应用.二阶锥互补问题（SOCCP）的一般形式为寻找向量x，y∈Rn及ξ∈Rn，使得问题（1）

成立.其中〈·，·〉为欧几里得内积，F：Rn→Rn与G：Rn→Rn均为光滑函数，K＝Kn1×…×KnN，N，n1，…，nN≥1，n1＋…＋nN＝n，Kni∶＝｛（x1x2）给定矩阵M∈Rn×n及向量q∈Rn，当x＝ξ，y＝F（ξ），F（ξ）∶＝Mξ＋q时，问题（1）即为二阶锥线性互补问题.

确定性的二阶锥互补问题在研究数学规划、运筹学、博弈论中具有非常重要的意义，而现实问题通常具有不确定性，因此带有随机因素的二阶锥线性互补问题越来越多地受到人们的重视.当F：K×Ω→K为带有随机变量的向量值函数，即F（x，ω）∶＝M（ω）x＋q（ω）时，随机二阶锥线性互补问题作为二阶锥互补问题的一个扩展便产生了，即

其中M（ω）∈Rn×n，q（ω）∈Rn.Ω，（Ω，F，P）为概率空间.

解决二阶锥互补问题有许多的方法，如内点法［1－2］、光滑化牛顿法［3－4］、光滑正则化方法［5］、优值函数法［6］及近似梯度下降法［7］等.后3种方法需要以二阶锥互补函数为基础.

特别地，若函数：Rl×Rl→Rl满足下列条件则称其为与x∈Kl（l≥1）有关的二阶锥互补函数［8］．常见的二阶锥互补函数为向量值Fischer－Burmeister（FB）函数，即

本文将引入期望残差最小化（ERM）方法［9］来解决随机二阶锥线性互补问题，给出利用ERM方法解决随机二阶锥线性互补问题的模型，即为寻找向量x∈K使得互补问题的期望残差最小：

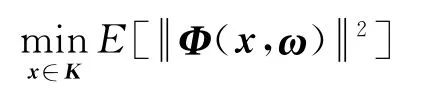
其中Φ：K×Ω→K定义如下：

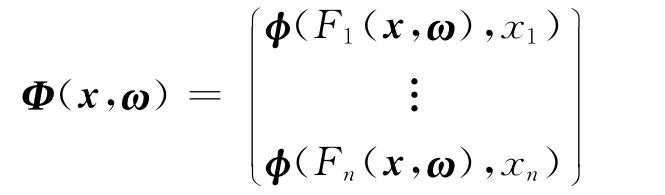
由互补问题产生多个相关的随机方程，期望残差方法可以看作是最小二乘法的自然扩展.本文中，以FB函数为例来求解随机二阶锥互补问题，即为FB函数，（x，y）＝x＋y－（x2＋y2）1／2.

1 预备知识

1.1 若尔当积

与标量乘法和矩阵乘法不同，若尔当积不具有结合律，这也是研究SOCCP 比较复杂的主要原因.下面给出若尔当积的定义和常用性质［4，8］.

通常将x2表示为x·x，将x＋y表示为相应分量的和，即x2＝x·x，x＋y＝（x1＋y1x2＋y2）.

下面给出·、＋与单位元e＝（1 0 …0）∈Rn的一些基础性质：

性质1

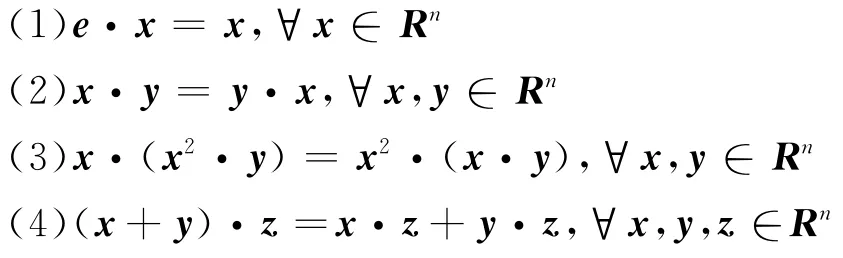
若尔当积与二阶锥可以通过以下常用的性质联系起来．

性质2

（2）若det（x）≠0，则称向量x＝（x1x2）∈R×Rn－1为可逆的，且-y＝（y1y2）∈R×Rn－1，使得x·y＝e，称y为x的逆，记为x－1．计算公式为由上式显然可得，x∈intK当且仅当x－1∈intK．

（3）若x∈K，则K中存在一个向量，记之为x1／2，满足（x1／2）2＝x1／2·x1／2＝x.计算公式为x1／2其中若x2＝0且s＝0，则定义为零向量，即x＝0.

1.2 谱分解

谱分解的定义及本文中将用到的相关性质［4，6］叙述如下.

其中i＝1，2，w为Rn－1中满足的任意向量.

若x2≠0，则x的谱分解形式唯一.

λ1、λ2和μ（1）、μ（2）的一些有趣的性质总结如下.

（1）谱向量μ（1）与μ（2）在若尔当积下是正交的，且长度为即μ（1）·μ（2）＝0，μ（1） ＝

（2）谱向量μ（1）与μ（2）在若尔当积下是幂等的，即μ（i）·μ（i）＝μ（i），i＝1，2.

（3）谱值λ1与λ2是非负的（正的）当且仅当x∈K（x∈intK）.

（4）x的行列式、迹及欧式范数均可以由谱值λ1与λ2表 示：det（x）＝λ1λ2，tr（x）＝λ1＋λ2，

2 解的存在性与收敛性

考虑下列问题：

其中ρ：Ω→R＋为连续密度函数且满足

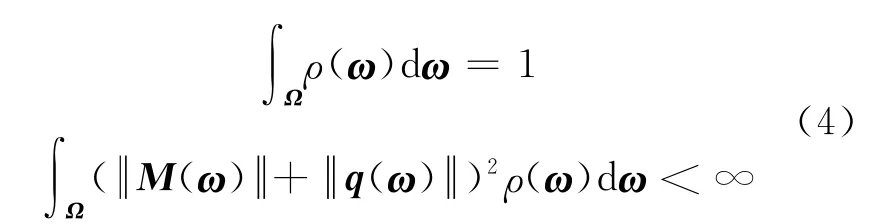
证明 因为x∈K，x＝（x1x2）∈R×Rn－1，所以由谱分解的定义与性质可得，存在λi、μ（i），i＝1，2使得x＝λ1μ（1）＋λ2μ（2），x2＝λ21μ（1）λ42）.所以

引理2x∈K，y∈K，（x－y）2＝x2＋y2－2x·y.

易得（x－y）2＝x2＋y2－2x·y.

现在，将利用拟蒙特卡罗方法进行积分计算.特别地，利用转换函数ω＝μ（）将Ω上的积分转化为单位立方体［0，1］n上的积分并在单位立方体中产生变量｛，i＝1，…，N｝.从而，f（x）可以表示如下：

下面将着重研究式（3）的离散近似问题的性质.

定义

其中I＝｛1，…，Nk｝，Ωk∶＝｛ωi，i＝1，…，Nk｝是由拟蒙特卡罗方法产生的变量集且满足ΩkΩ，当k→∞时Nk→∞.

式（6）中，尾项［10］具有重要意义，是保证f（k）（x）水平集非空有界的重要条件，在文献［6］中有详细证明.

由Φ（·，ω）的连续性可得，f（k）（x）为连续函数.定义的最优解集为的最优解集为Sk，函数f的水平集为D（γ）∶＝｛x∈Rn｜f（x）≤γ｝.

定理1 设｜〈x，F（x，ω）〉｜≤M，M为一正的常数且对ω∈Ω，M（ω）与q（ω）不同时为0，则对任意给定的

证明

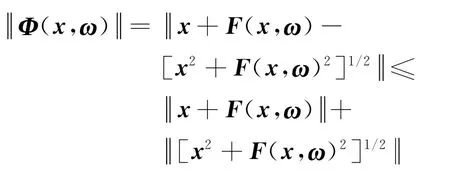
为简便公式，设a∶＝x，b∶＝F（x，ω），则由引理可得

从而

因为

所以，当Nk→∞时

由式（4），且对任意确定的x∈K，是连续的，非负有界.因此，由数列分布的收敛性分析可得

注 随机二阶锥线性互补问题中〈x，F（x，ω）〉＝0，若｜〈x，F（x，ω）〉｜无界，则与原问题偏离太大，所以题设条件｜〈x，F（x，ω）〉｜≤M具有其合理性.

引理3［6］假设F（x，ω）：R→R可微单调，且存在使得∈intK，F（x，ω）∈intK，则对任意的γ≥0，水平集D（γ）∶＝｛x∈R｜f（k）（x）≤γ｝非空有界.

证明 因为对任意的ω∈Ω，M（ω）为半正定的，F（x，ω）∶＝M（ω）x＋q（ω）.

由引理3可得，对任意的γ≥0，水平集D（γ）∶＝｛x∈Rn｜f（k）（x）≤γ｝非空有界.

易知，对 任 意 确 定 的ω，Φ（x，ω）是 全 局Lipschitz 连 续 的［9］，即 对 任 意 的x，y∈Rn，其 中L（ω）为与ω有关的正常数.易得，存在C1＞0，使得

与定理1类似可证明，-C0＞0，使得对1）.由引理3可得，水平集D（γ）是闭且有界的，因此可定义从而，

其中C∶＝2C0C1（1＋C2）.

由对密度函数ρ的假设及题设条件可得

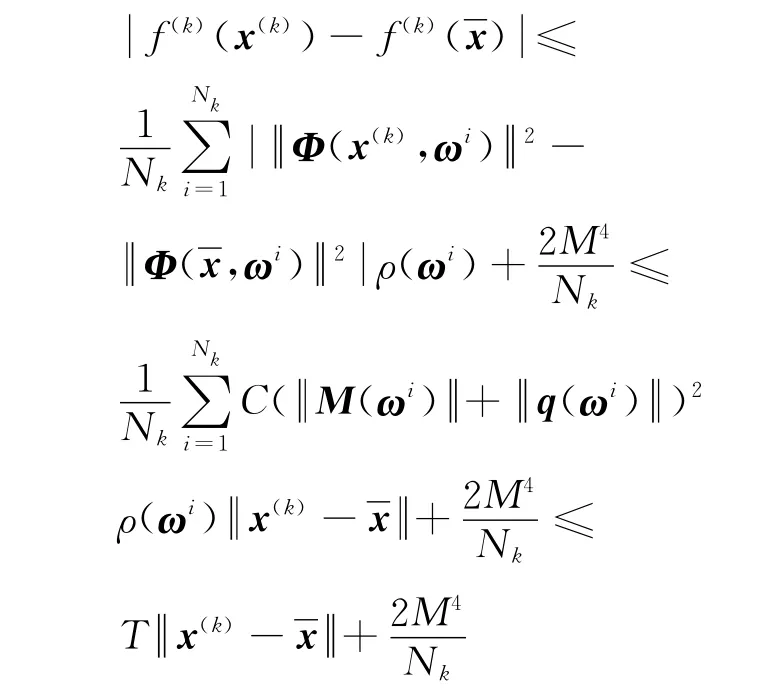
其中T为常数，且对所有充分大的k，T≥从而当k→∞时，

又因为f（k）（x）→f（x），所以，当k→∞时，

由定义可得，对任意的x∈K，f（k）（x（k））≤f（k）（x）.所以，综上所述可得

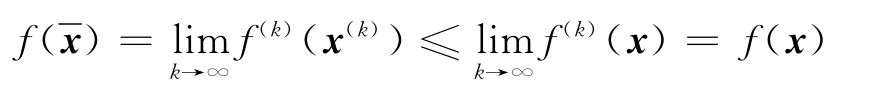
即证得｛x（k）｝的所有聚点均包含在S内.

注 若-γ≥0，使得D（γ）∩K＝，则Sk∩K＝，即目标函数无解.从而，定理的假设是合理的.

3 结 语

FB函数是一类重要的二阶锥互补函数，本文通过它将随机二阶锥线性互补问题转化为求解目标函数的极小化问题.据了解，这是首次在二阶锥范围内利用期望残差最小化方法来解决随机线性互补问题.本文对题设条件进行了合理假设并着重证明了离散型目标函数解的存在性与收敛性.

［1］ Alizadeh F，Goldfarb D.Second－order cone programming ［J］.Mathematical Programming，2003，95（1）：3－51.

［2］ Andersen E D，Roos C，Terlaky T.On implementing a primal－dual interior－point method for conic quadratic optimization［J］.Mathematical Programming，2003，95（2）：249－277.

［3］ Chen X D，Sun D，Sun J.Complementarity functions and numerical experiments on some smoothing Newton methods for second－order－cone complementarity problems ［J］.Computational Optimization and Applications，2003，25（1－3）：39－56.

［4］ Fukushima M，Luo Z Q，Tseng P.Smoothing functions for second－order－cone complementarity problems ［J］.SIAM Journal on Optimization，2002，12（2）：436－460.

［5］ Hayashi S，Yamashita N，Fukushima M.A combined smoothing and regularization method for monotone second－order cone complementarity problems ［J］.SIAM Journal on Optimization，2005，15（2）：593－615.

［6］ Chen J S，Tseng P.An unconstrained smooth minimization reformulation of the second－order cone complementarity problem ［J］.Mathematical Programming，2005，104（2－3）：293－327.

［7］ Pan S，Chen J S.A proximal gradient descent method for the extended second－order cone linear complementarity problem ［J］.Journal of Mathematical Analysis and Applications，2010，366（1）：164－184.

［8］ Pan S，Chen J S.A damped Gauss－Newton method for the second－order cone complementarity problem［J］.Applied Mathematics and Optimization，2009，59（3）：293－318.

［9］ Chen X，Fukushima M.Expected residual minimization method for stochastic linear complementarity problems ［J］.Mathematics of Operations Research，2005，30（4）：1022－1038.

［10］ Yamashita N，Fukushima M.A new merit function and a descent method for semidefinite complementarity problems［M］／／Reformulation：Nonsmooth，Piecewise Smooth，Semismooth and Smoothing Methods.New York：Springer US，1999：405－420.