高压下钨弹性和热力学性质的第一性原理研究

张修路，罗 雰，郭志成，遆瑞娟，刘中利，刘成安，蔡灵仓

(1. 西南科技大学极端条件物质特性实验室，绵阳621900;2. 洛阳师范学院物理与电子信息学院，洛阳471022;3. 中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，绵阳621900)

1 引 言

由于具有较高的强度、耐磨性、耐腐蚀性和高熔点，金属钨及其合金在航空航天、原子能和电子工业等领域有着广泛的应用，尤其是高温高压极端条件下使用的首选材料之一. 例如在金刚石压砧实验中，钨常被作为样品的支撑材料［1］. 钨及其合金的高压物性有着重要的应用背景，国内外科研人员对其进行了大量研究，得到了一系列有益的结果［2-7］，但是，目前对钨及其合金的性质认识仅限制在一定的压力范围内，并且由于实验数据的缺少从而难以形成规律性的认识;在高温高压极端条件下的认识更为缺乏. 此外，对于钨在高温高压下相结构的稳定性和相边界问题，动、静高压实验存在着难以解释的巨大分歧［3］，影响了其进一步的应用.

1992 年，Hixson 等人［8］根据Hügoniot 状态方程测量结果中冲击波速度-粒子速度关系曲线以及由此导出的压强-比容关系曲线的拐折判断相变的发生并确定相变发生的冲击压强区间，他们的结果表明钨在大约200 GPa 处发生固固相变. 理论上，Moriarty［9］在对各个可能相钨的自由能进行第一原理计算后发现，零温下体心立方(bcc)结构钨在1250 GPa 压强范围内是稳定的，之后将转变为密堆六方(hcp)结构. 钨在高温高压下是否发生固-固相变、高压固相的结构、相边界等问题仍然没有明确的结论，而固-固相变问题是解释动、静高压实验关于钨的熔化曲线(固-液相边界)研究结果间巨大分歧［3］的关键所在. 因此，我们拟深入研究钨的弹性性质和热力学性质，进而了解钨的高压力学稳定性，以对现有的钨高压数据库进行补充或修正.

本文采用密度泛函理论详细研究了bcc 结构钨的弹性常数，进一步分析了高压下钨的力学稳定性，利用准谐德拜模型研究钨在高温高压下的热力学性质.

2 计算方法

本文采用基于平面波赝势的密度泛函理论计算方法，所用软件为CASTEP［10］，电子间相互作用的交换关联势采用广义梯度近似(GGA)的Perdew-Burke -Ernzerhof 势［11］. 在计算中，钨的离子组态选取的是5s25p65d46s2;布里渊区积分采用Monkhorst-pack 方法［12］，对布里渊区进行采样所使用的k 点为30 ×30 ×30;平面截断能取600 eV;自洽循环的收敛精度为5 ×10-7eV/atom. 在几何优化中，采用的是BFGS 算法，达到收敛的标准被设置为:原子的能量偏差小于5 ×10-7eV/atom，最大应力偏差小于0.05GPa，最大位移偏差小于

0.001Å.

为了研究晶体的热力学性质，采用了准谐德拜模型. 在此模型中，钨的非平衡Gibbs 函数G*(V，P，T)形式如下［13］:

其中E(V)是晶体的总能量，PV 对应于静态压缩过程，Avib是 Helmholtz 振 动 自 由 能，可 以 表 示为［14-16］:

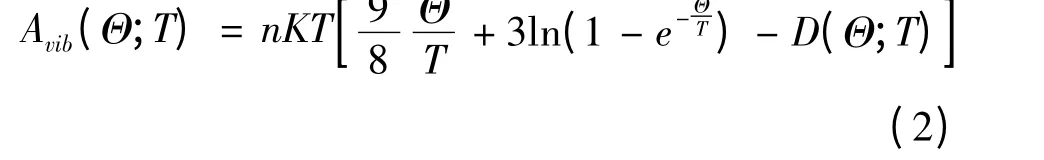
其中Θ(V)是德拜温度，n 是原胞中原子的个数.对于各向同性固体来说，泊松比σ =0.25［17］，德拜温度可表示为［18］:

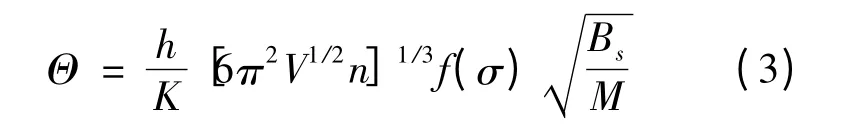
其中M 是每个原胞中分子的质量，f(σ)的表达式由文献［15］给出，BS是用来表示晶体压缩率的绝热体模量，表达式为［13］:

非平衡Gibbs 函数G* (V，P，T)对体积求最小值，即

通过(5)式可以得到晶体的热状态方程V(P，T)，等温弹性模量BT，等容热容CV，熵S，热膨胀系数α以及等压热容CP分别用如下形式表示:

3 结果与讨论

对于bcc 结构钨，计算不同晶格常数下的体系总能E，得到体系的总能E 和相对应的原胞体积V的关系. 将计算得到的E -V 数据通过四阶有限应变状态方程［19］进行拟合，从而得到bcc 结构钨的晶格常数a，体积弹性模量B 以及其对压强的一阶偏导B'，计算结果如表1 所示. 可以看到，晶格常数和体积弹性模量的计算结果与实验值［20］和理论值［21，22］都符合较好，其中晶格常数与实验值的误差小于0.5%.

表1 bcc 结构钨的晶格常数a，体积弹性模量B0 及其对压强的一阶偏导B'Table 1 The lattice constant a，the bulk modulus B0 and its pressure derivative B' of bcc phase W

bcc 结构钨有3 个弹性常数，见表2. 常压下bcc 结构钨的弹性常数计算值为C11=511.1 GPa、C12= 201.2 GPa、和C44= 134.7 GPa，与与实验值［23］相符合，与密度泛函理论得到的理论值［21，22］相接近，其中C11与C12的理论值与实验值小于5%，C44偏差最大为17%.

在常压下bcc 结构钨的弹性常数计算值与实

表2 bcc 结构钨的弹性常数Cij、剪切模量G、体模量B 和杨氏模量ETable 2 The elastic constants Cij，bulk modulus B，shear modulus G and Young's modulus E for bcc phase W

验值符合较好的基础上，理论预测了高压下bcc 结构钨的弹性常数，如图1 所示. 可以看到钨的弹性常数随压强的增大都呈现增大的趋势. Koci［22］等人于2008 年对bcc 结构钨的弹性进行了从头算理论研究，他们只计算了300 GPa 范围内的弹性常数，而对于更高压强范围内的弹性性质并未报道.本文的工作考虑了0 -600 GPa 压力范围内压强对弹性常数的影响，所预测的结果与Koci 的理论值［22］符合得很好. 钨的弹性常数随压强的增加呈现增大的行为，在研究的压强范围内bcc 结构钨的力学性质稳定都满足如下标准:

图1 bcc 结构钨高压下的弹性模量Fig. 1 Pressure dependences of the elastic constants for bcc W

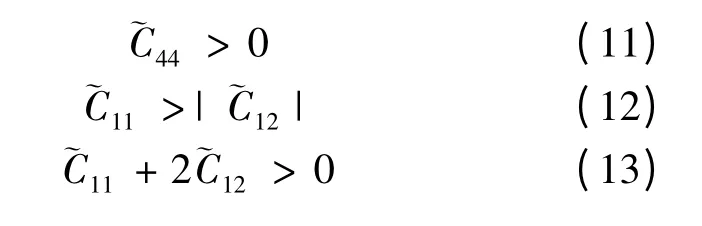
其中

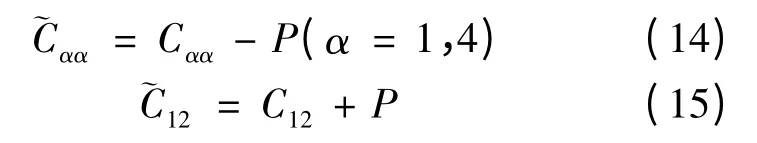
这表明在研究的压强范围内bcc 结构的钨是力学结构稳定的，不会发生相结构转变.

根据理论预测的bcc 结构钨的弹性常数，对钨的力学强度进行研究. 采用Voigt-Reuss-Hill 近似［24］给出力学强度有关的体模量B 和剪切模量G

其中，

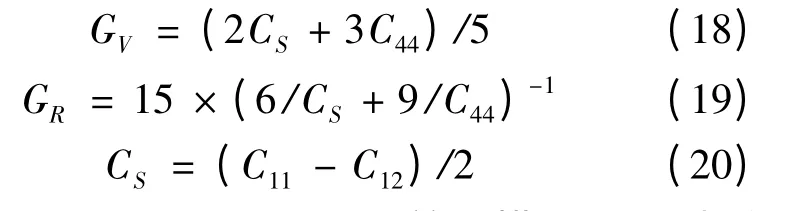
GV和GR分别是Voigt 和Reuss 剪切模量. 通过弹性常数计算得到的体模量与拟合状态方程得到的体模量的数值很接近，表明本工作所采用计算弹性常数的模型是可靠的. 从表3 中可以看出，随着压强的增加体模量和剪切模量都会单调增加.

Pugh［25］指出，体模量与剪切模量的比值B/G可以作为体系韧性和脆性的一种量度. 体模量表示体系发生断裂的阻力，体模量越大越不容易断裂;剪切模量表示体系发生塑性变形的阻力. B/G的比值越大，表示体系易发生塑性变形且不容易断裂，意味着体系的韧性度越高;相反地，B/G 的数值越低表示体系不易发生塑性变形且容易发生断裂，意味着体系的脆性越高. 如果B/G ＞1.75，材料的力学性能体现为韧性而不易断裂;反之，则表现为脆性而容易发生断裂. 在零温零压下，bcc 结构钨的B/G 比值为2.136，因此体系的力学性能表现为韧性. 随着压强的增加B/G 的比值会进一步的增大，bcc 结构钨韧性会增强.

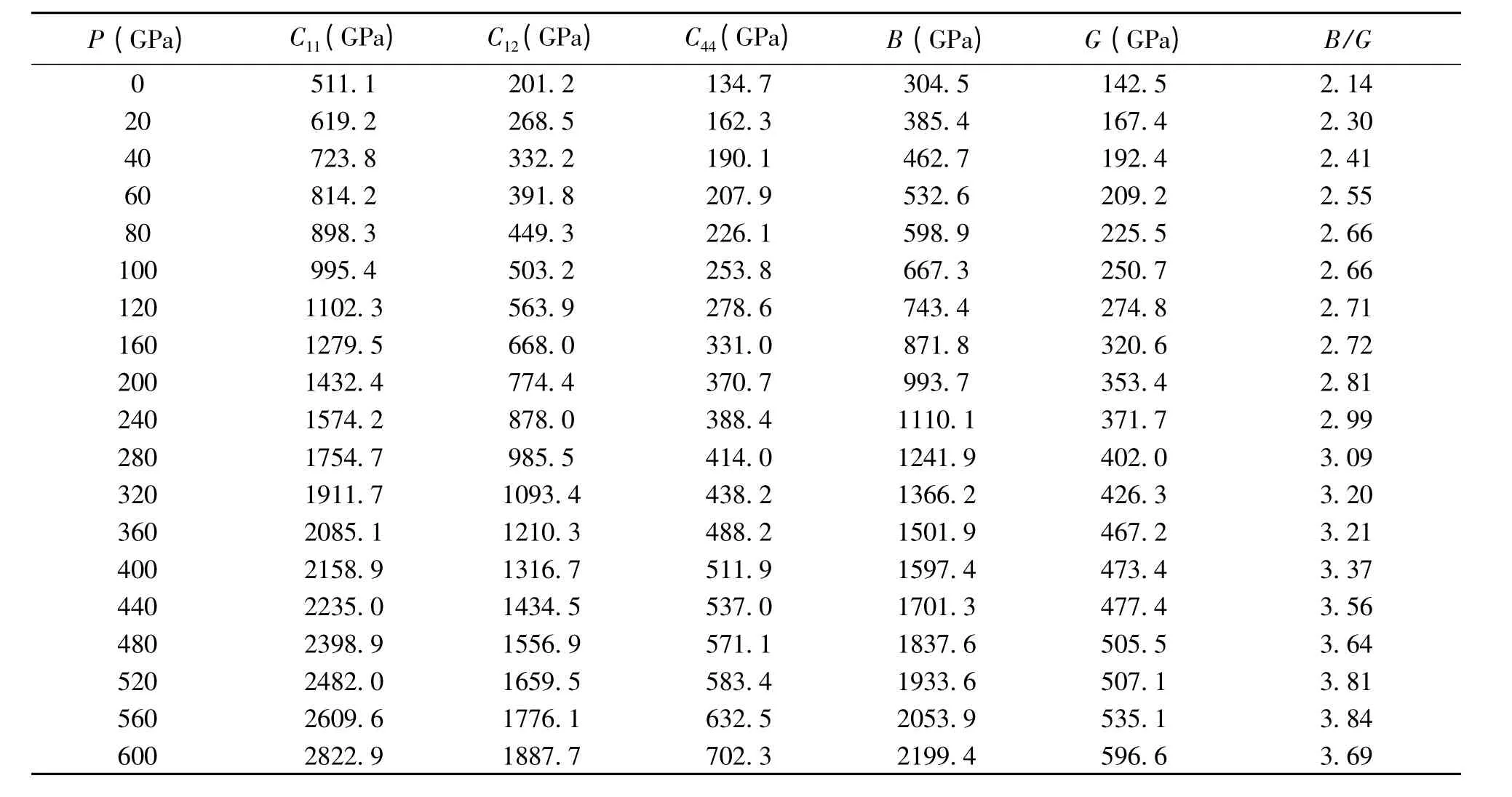
表3 bcc 结构钨的弹性常数、体模量和剪切模量Table 3 The pressure dependences of the elastic constants，bulk modulus and shear modulus for bcc phase W

根据准谐德拜模型，预测了bcc 结构钨在高温高压范围内的热力学性质. 图2 表示的是bcc 结构钨的热膨胀系数α 随压强和温度的变化关系.弹性常数随温度的变化与实验值［26］相吻合，而理论计算值略高于实验值，这是由于GGA 近似高估了晶格常数的缘故. 从图中可以看出，给定压强下，低温区热膨胀系数随温度的升高增加更为明显，而高温区随温度的增加热膨胀系数增加较平缓，说明低温下体系的热膨胀效应更明显，高温下的热膨胀效应明显地受到抑制;在一定温度下，热膨胀系数随压强的增加而减小. 由此可以看出，升高温度和降低压强对bcc 钨的热膨胀性质影响是等效的.

图2 bcc 结构钨热膨胀系数α 与温度和压强的关系Fig. 2 Temperature and pressure dependences of the thermal expansion coefficient α for bcc W

图3 给出了bcc 结构钨的等容热容CV随温度和压强的变化关系. 从图中可以看出，给定压强下，热容随温度的增加而增加，在高温区热容增加至常数，继续升温将不会改变，这符合Dulong -Petit 极限，即高温下体系的等容热容3R(R =8.314 J·mol-1·K-1)，而且初始升温阶段(0 ～300 K)低压下热容随温度的变化较高压下更明显.在低温下，随着压强的增加热容会减小，但是在高温下，高压区和低压区的热容都会趋于一个常数.图4 给出了bcc 结构钨的等压热容CP随温度和压强的变化关系. 可以看出，低温下CP随压强的升高下降很快，但是在高温区随压强的增大它对温度的依赖性减弱. 图5(a)为bcc 结构钨的熵随着温度的变化曲线，可以看出，熵随着温度的增加而增加.图5(b)显示bcc 结构钨的熵在不同温度下随压力的变化关系，可以看出，熵随着压力增加而减小.

图3 bcc 结构钨等容热容CV 与温度和压强的关系Fig. 3 Temperature and pressure dependences of the heat capacity CV for bcc W

图4 bcc 结构钨等压热容Cp 与温度和压强的关系Fig. 4 Temperature and pressure dependences of the heat capacity Cp for bcc W

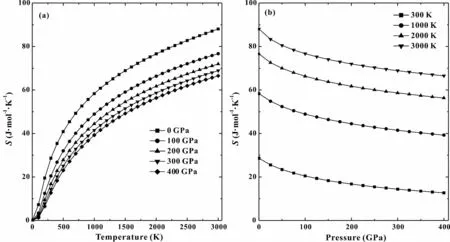
图5 bcc 结构钨熵S 与温度和压强的关系Fig. 5 Temperature and pressure dependences of the entropy S for bcc W

4 结 论

本文采用密度泛函理论平面波赝势广义梯度近似(GGA)的第一性原理方法研究了bcc 结构钨的弹性性质和热力学性质. 计算得到的bcc 结构钨的晶格常数、体弹模量以及其对压强的一阶偏导与实验值符合较好. 理论预测常压下钨的弹性常数与实验值符合的较好. 高压下的弹性常数满足力学稳定判断标准，表明高压下bcc 结构是钨的稳定结构. 此外，本文也预测了体模量和剪切模量随压强变化关系. 在零温零压下，bcc 结构钨的B/G比值为2.136，因此体系的力学性能表现为韧性，在高压下其韧性会增强. 利用准谐德拜模型我们成功预测了bcc 结构钨的热膨胀系数、等容热容、等压热容和熵随着压强和温度的变化关系. 这些认识有利于我们对高温高压下钨性质的理解和预测，为钨及其合金的进一步合理利用提供依据.

［1］ Hemley R J，Mao H K，Shen G Y，et al. X-ray imaging of stress and strain of diamond，iron，and tungsten at megabar pressure［J］. Science，1997，276:1242.

［2］ He D W，Duffy T S. X -ray diffraction study of the static strength of tungsten to 69 GPa［J］. Phys. Rev.B，2006，73:134106.

［3］ Errandonea D，Schwager B，Ditz R，et al. Systematics of transition - metal melting ［J］. Phys. Rev. B，2001，63:132104.

［4］ Millett J C F，Bourne N K，Rosenberg Z，et al. Shear strength measurements in a tungsten alloy during shock loading［J］. J. Appl. Phys.，1999，86:6707.

［5］ Zhou X M，Jing F Q，Hu J B. Sound speed in a shocked tungsten alloy:its significance in studying“softening”mechanism to multiphase alloys ［J］.Chin. Phys. Lett.，1996，13:761.

［6］ Zhang W J，Yang Z Z. Studies on the fracture behaviour for 93 tungsten alloy［J］.Chin. J. High Pressure Phys，1995，9:279 (in Chinese)［张万甲，杨中正.93 钨合金断裂特性研究［J］. 高压物理学报，1995，9:279］

［7］ Wang J G，Shi W F. Compressive property and equation of state of 4.2Ni2.45Fe0.35CoW alloy under pressure from 100 GPa to 500 GPa ［J］. Chin. J. High Pressure Phys.，1995，9:195 (in Chinese)［王金贵，施卫丰. 100 ～500 GPa 4.2Ni2.45Fe0.35CoW 合金的冲击压缩性和物态方程研究［J］. 高压物理学报，1995，9:195］

［8］ Hixson R S，Fritz J N. Shock compression of tungsten and molybdenum ［J］. J. Appl. Phys.，1992，71:1721.

［9］ Moriarty J A. Ultrahigh-pressure structural phase transitions in Cr，Mo，and W［J］. Phys. Rev. B，1992，45:2004.

［10］ Segall M D，Lindan P J D，Probert M J，et al. Firstprinciples simulation:ideas，illustrations and the CASTEP code［J］. J. Phys.:Condens Matt.，2002，14:2717.

［11］ Perdew J P，Burke K，Ernzerhof M. Generalized gradient approximation made simple ［J］. Phys. Rev.Lett.，1996，77:3865.

［12］ Monkhorst H J，Pack J D. Special points for Brillouin-zone integrations ［J］. Phys. Rev. B，1976，13:5188.

［13］ Blanco M A，Francisco E，Luaña V. GIBBS:isothermal - isobaric thermodynamics of solids from energy curves using a quasi - harmonic Debye model ［J］.Comput. Phys. Commun.，2004，158:57.

［14］ Francisco E，Recio J M，Blanco M A，et al. Quantum- mechanical study of thermodynamic and bonding properties of MgF2［J］. J. Phys. Chem. A，1998，102:1595.

［15］ Francisco E，Blanco M A，Sanjurjo G. Atomistic simulation of SrF2polymorphs［J］. Phys. Rev. B，2001;63:094107.

［16］ Flórez M，Recio J M，Francisco E，et al. First-principles study of the rocksalt - cesium chloride relative phase stability in alkali halides［J］. Phys. Rev. B，2002，66:144112.

［17］ Poirier J P. Introduction to the physics of the earth's interior［M］. England:Cambridge University Press，1991.

［18］ Blanco M A，Martín Pendás A，Francisco E，et al.Thermodynamical properties of solids from microscopic theory:applications to MgF2and Al2O3［J］. J. Molec.Struct. Theochem，1996，368:245.

［19］ Birch F. Equation of state and thermodynamic parameters of NaCl to 300 kbar in the high -temperature domain［J］. J. Geophys. Res.，1986，91:4949.

［20］ Kushwaha S S，Sharmab M P，Tomar Y S. An equation of state for molybdenum and tungsten［J］. Physica B，2003，339:193.

［21］ Bercegeay C，Bernard S. First -principles equations of state and elastic properties of seven metals ［J］.Phys. Rev. B，2005，72:214101.

［22］ Koci L，Ma Y M，Oganov A R，et al. Elasticity of the superconducting metals V，Nb，Ta，Mo，and W at high pressure［J］. Phys. Rev. B，2008，77:214101.

［23］ Featherston F H，Neighbours J R. Elastic constants of tantalum，tungsten，and molybdenum ［J］. Phys.Rev.，1963，130:1324.

［24］ Strachan A，Cagin T，Goddard III W A. Phase diagram of MgO from density -functional theory and molecular - dynamics simulations ［J］. Phys. Rev. B，1999，60:15084.

［25］ De Koker N，Stixrude L. Self - consistent thermodynamic description of silicate liquids，with application to shock melting of MgO periclase and MgSiO3perovskite［J］. Geophys. J. Int.，2009，178:162.

［26］ Litasov K D，Gavryushkin P N，Dorogokupets P I，et al. Thermal equation of state to 33.5 GPa and 1673 K and thermodynamic properties of tungsten［J］. J. Appl. Phys.，2013，113:133505.