变系数EKdV模型在模拟南海北部大振幅内孤立波传播和裂变中的应用*

张善武， 范植松**， 石新刚

(1.中国海洋大学海洋环境学院，山东 青岛 266100；2.中国船舶信息中心，北京 100020)



变系数EKdV模型在模拟南海北部大振幅内孤立波传播和裂变中的应用*

张善武1， 范植松1**， 石新刚2

(1.中国海洋大学海洋环境学院，山东 青岛 266100；2.中国船舶信息中心，北京 100020)

利用垂向连续分层变系数EKdV模型，模拟了南海北部海域大振幅内孤立波的传播和裂变过程，并与观测数据进行比较。结果表明：连续分层变系数EKdV模型能够较好地反映振幅小于100 m的内孤立波的振幅和波宽，对于更大振幅的强非线性内波，该模型模拟的振幅和波宽均较实测较小；非线性模态函数能够较准确地反映温度振荡的垂直结构，而水平流速的大小和垂直结构则与线性模态较符合。研究结果表明，变系数EKdV模型能够为研究和理解大振幅内孤立波的传播和裂变过程提供较好的理论支持。

内孤立波； 非线性； 裂变；南海

南海北部是世界上已观测到内孤立波活动最为强盛的海域之一，该海域内孤立波具有大振幅、强非线性以及能够长距离传播等特征。Klymak等[1]在南海北部深水区观测到的内孤立波振幅达到170 m，半波宽度可达3 km，相速度约为(2.9±0.1)m·s-1。亚洲海洋国际声学实验(ASIAEX)期间，Ramp等[2]在南海北部陆坡海域观测到超过140 m的大振幅内孤立波，从其生成源地到该海域的传播距离约为485 km 。

内孤立波的长距离传播通常被认为是非线性和频散共同作用的结果，可由Korteweg deVries(KdV)方程及该方程的其它演变形式来表示。观测到的内孤立波的基本特征，如垂直模态、波形、相速度以及波形的传播裂变等可以利用KdV理论较为合理地解释。近几年来，国内外很多学者为此做了大量工作。Yang等[3]在南海北部东沙附近海域的研究表明较小振幅的第一模态内孤立波的波形与KdV方程理论解符合得很好。Ramp等[2]通过比较观测和理论计算的内孤立波相速度以及半波宽度等量，发现两层高阶KdV(EKdV)理论计算的相速度和半波宽度都要更接近观测，但对于大振幅(>88 m)内孤立波，该理论失效。Du等[4]利用一个两层变系数EKdV模型，在考虑耗散项的情形下，模拟了南海北部内孤立波传播和裂变过程，并试图解释ASIAEX期间观测到的“b”型内波的成因。尽管观测到的内孤立波通常具有很强的非线性，往往超出KdV理论的弱非线性假设，KdV理论在解释内孤立波的诸多观测特征方面仍然具有重要作用[5]。Fan等[6]利用连续分层的一般化的KdV方程研究了南海北部大振幅内孤立波的传播和裂变过程，发现背景涨潮流和落潮流对裂变生成的孤立子的波长有明显的不同作用。产生该不同作用的主要原因是在涨潮流和落潮流时段，背景流引起非线性系数的差异。Si等[7]基于连续分层的一般化的KdV方程研究了南海北部大振幅内孤立波对桩柱的剪切力和力矩作用，取得显著的改进成果。Xu等[8]利用两层的KdV理论研究了南海西北部内孤立波对热带风暴的响应。Cai和Xie[9]借助一个两层的一般化二维EKdV模型，研究了内孤立波在南海东北部东沙附近海域的传播和裂变过程及其非线性相互作用。

由于南海北部内孤立波具有大振幅和强非线性特征，模拟该海域的内孤立波时，需要考虑高阶非线性的作用。在实际应用中，由于水深和层结等的变化，两层模型往往具有很大的局限性，因此，需要进一步建立一个连续分层的模型。Grimshaw等[10]系统回顾了连续分层变系数高阶非线性EKdV模型的推导，将其应用于南海内孤立波传播和裂变的研究，并给出了2个计算实例，但并没有与现场观测进行对比。在考虑地转效应和背景流场的情况下，Zhang和Fan[11]进一步将该模型用于模拟南海北部大振幅内孤立波由深海向陆坡海域的传播和裂变过程，同样地，也仅仅给出了数值结果。本文在Zhang和Fan[11]的研究基础上，利用ASIAEX现场观测的温度和流速资料，对变系数EKdV理论模型的数值结果进行了对比验证。结果显示，变系数EKdV模型在模拟大振幅内孤立波传播和裂变上具有一定的可行性。

1 理论模型

Grimshaw等[12]从一个无黏不可压缩2维欧拉方程出发，推导了一个综合考虑真实海洋地形变化和背景流场的简化模型：

(1)

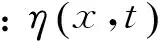
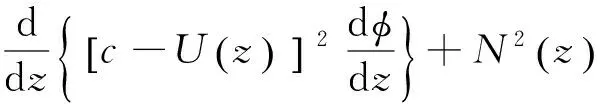
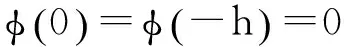
(2)

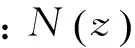
(3)

(4)

(5)

(6)

(7)

(8)

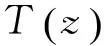
(9)

及边界条件：

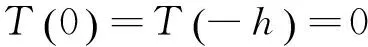
(10)

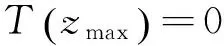
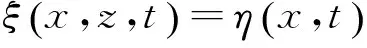
(11)

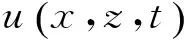
(12)

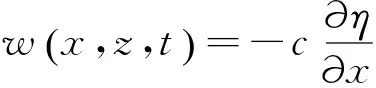
(13)

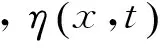
(14)

方程(1)进一步化为：

(15)

如果考虑底摩擦等因素，例如在方程(15)中加入Chezy形式的底摩擦项，则可以得到方程：

(16)

其中：k为底摩擦系数。方程(16)可作为研究一维孤立波传播的一般模式。模拟波形变化时，通常输入一个随时间变化的波形(孤立波或者正弦波形)作为边界条件，其一般形式为：

(17)

其中：F是一个随时间变化的函数(周期或者非周期函数)。

2 模型应用

利用变系数EKdV模型模拟内孤立波波形传播的一般步骤为：

(1) 解本征值问题(2)，获得长内波相速度c及线性模态函数φ的值；

(2) 解本征问题(9)、(10)，获得模态函数非线性修正项T的值；

(3) 计算系数(3)～(6)；

(4) 输入波形(17)，求方程(16)的数值解；

(5) 计算(11)～(13)获得实际的等密度面位移，水平流速和垂向流速。

2.1 观测数据

ASIAEX前期实验开始于2000年春季，主要实验时间从2001年4～5月，是一次成功的国际合作的声学观测实验，除了声学实验结果，期间更获得了丰富的南海北部东沙附近海域的内波观测资料，包括温度和流速的锚系观测资料，以及一些走航观测资料。这些观测数据为研究这一海域的内波尤其是内孤立波的传播特性提供了很好的参考。2001年的观测资料可以从网站ftp://acoustics.whoi.edu/data/asiaex01/免费下载[15]。本文选取了其中一个站位(S7)的温度和流速数据，该站位位于(21.61°N，117.28°E)，水深350m(见图1)。

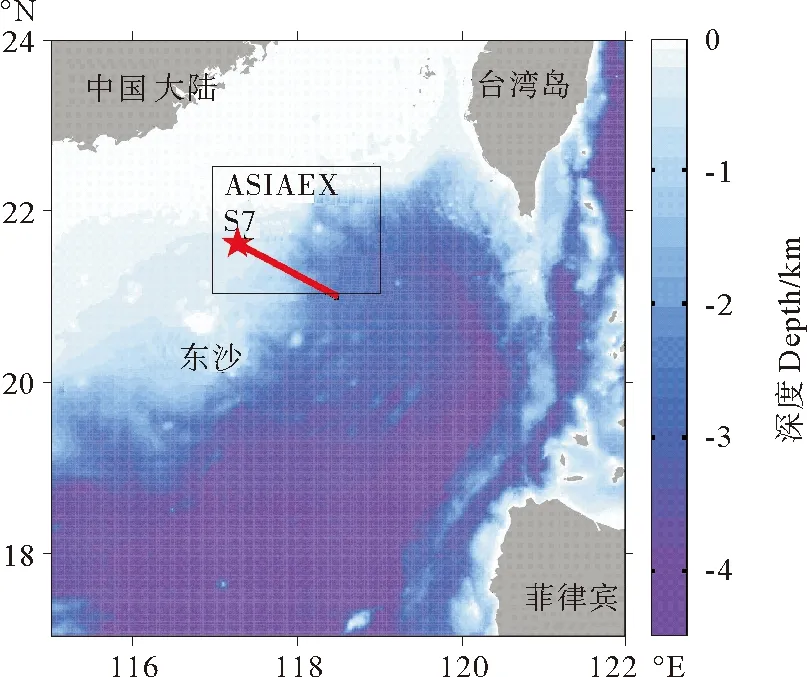
图1 南海东北部水深和ASIAEX区域观测站位(五星)、模拟断面(直线)示意图Fig.1 Bathymetry of northeast South China Sea,the moored location (pentagram) and the simulated cross-section (line)

2.1.1 温度 本文选取了S7站位从2001年4月22日12时～5月18日18时的各层温度数据，数据时间间隔为2min。图2给出了S7站位内孤立波引起的温度振荡时间序列，其中从原始数据中剔除了低通滤波得到的低频(周期>46h)和潮频(5～46h)数据，仅保留高频(周期<5h)的数据。图2可以清晰地看到由内孤立波引起的温度振荡可分为两簇(Cluster)，每簇中振幅较大的孤立波时间间隔约为24h，定义为“a”波，2个振幅较大的孤立波之间有一个振幅较小的波动，其时间间隔不定，定义为“b”波[2]。前一簇内孤立波引起的温度振荡较小，约为5 °C，后一簇内孤立波引起的温度振荡可达9～10°C，其对应的孤立波振幅要比前一簇大50m左右。从垂向结构上看，该站位观测到的内孤立波符合典型的第一模态内波特征，最大温度振荡约发生在深度140m左右。

2.1.2 流速S7站位由内孤立波引起的各层纬向流速时间序列如图3所示，该序列从原始流速数据中减去了低通滤波得到的低频和潮频数据，数据的时间跨度、取样间隔和处理方法与温度数据一致。从图3可以看到，流速垂向结构与温度振荡是对应的，从垂向结构上看，也符合第一模态内波的典型特征。内孤立波引起的纬向流速上层流向向西，与内孤立波传播方向一致，下层流向向东，与内孤立波传播方向相反。以5月8日的“a”波为例，由内孤立波引起的纬向流速在上层最大值约为1.25m·s-1，下层流速最大值较小，约为0.6m·s-1。 与温度振荡观测相比，由于流速观测数据的垂直分辨率较低，不能很好地估计流速转向点所在的深度，根据温度观测数据的分析结果，可以估计流速转向点所在深度大约在140m。

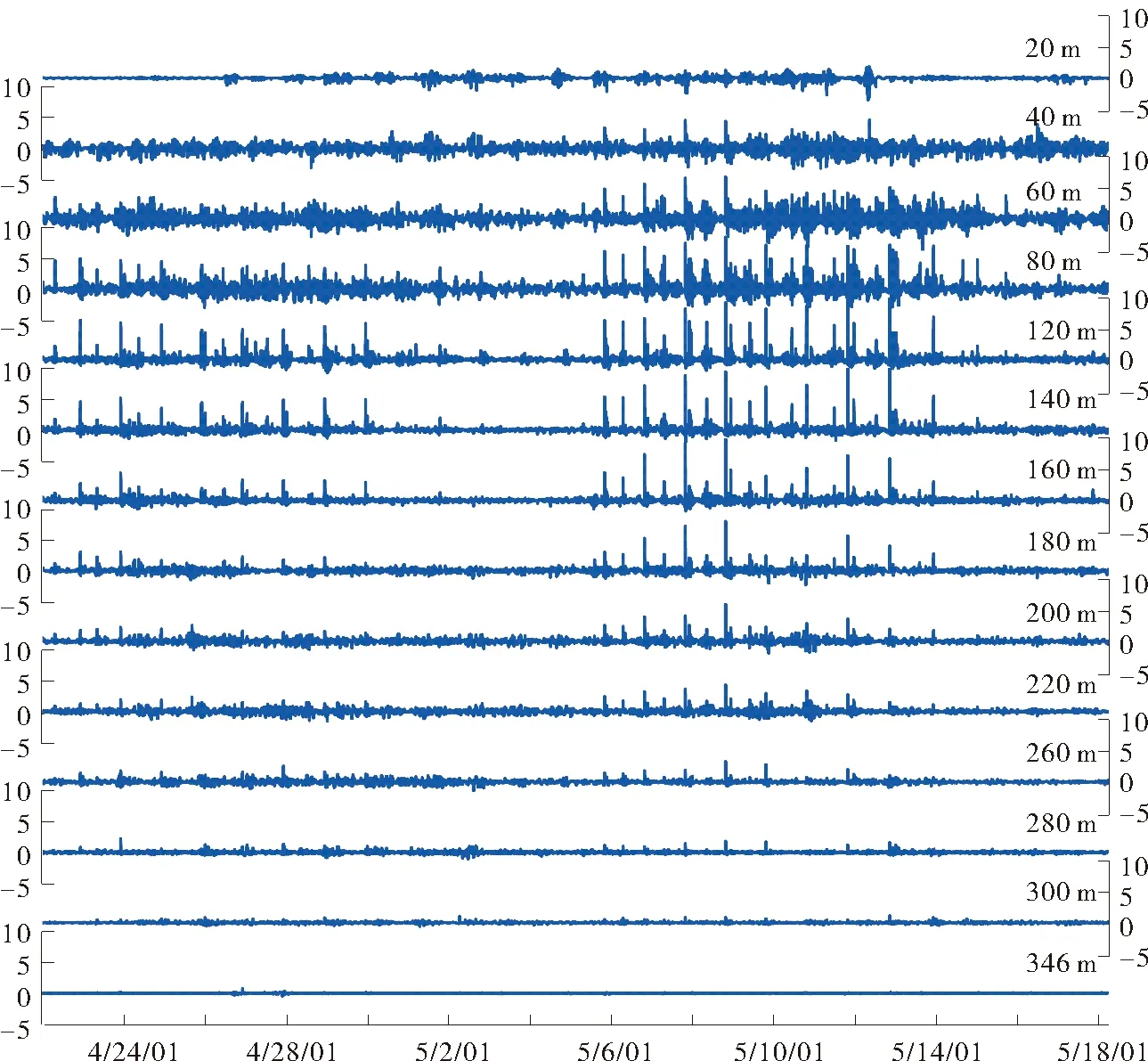
(图中纵坐标为温度(°C)；横坐标为时间(世界时)。The ordinate is temperature(°C)； The abscissa is time(GMT) in the figures.)图2 S7站位各层温度振荡Fig.2 Temperature oscillation at different depth of station S7

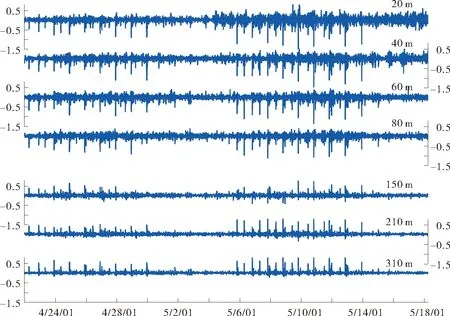
(图中纵坐标为纬向流速(m/s)；横坐标为时间(世界时)。The ordinate is zonal current speed(m/s)； The abscissa is time(GMT) in the figures.)图3 S7站位各层纬向流速Fig.3 Zonal current at different depth of station S7

2.2 理论模型结果

2.2.1 模拟断面 为了能够与S7站位的观测结果进行对比，需要确定观测站位内孤立波的生成源地和传播方向，从而确定内孤立波的传播路径。吕宋海峡被认为南海北部内波的生成源地，内波在此生成以后向西或者西北方向传播进入深水海盆。Ramp等[2]通过分析S7站位纬向流速阈值的统计结果，估计了通过该站位不同振幅孤立波的传播方向和可能生成源地，其结果显示，通过S7站位的大振幅内孤立波均来自吕宋海峡方向。本文选择的模拟断面起始站位位于(21°N，118.5°E)，终点站位为S7(见图1)，该断面所示路径方向为西偏北28°左右，接近Ramp等[2]的估计值。

2.2.2 温盐数据 模拟断面温度和盐度资料使用美国国家海洋大气局(NOAA)海洋资料中心(NODC)网站提供的WOA01数据集，空间网格分辨率为0.25°，该数据集为气候态平均数据，其中季节平均和年平均数据垂向为33层，月平均数据垂向为24层。本文选取5月份的月平均资料，使用立方插值获得模拟断面各个站位上的温盐剖面，从而计算这些站位的密度和浮力频率。在不考虑背景流场的情形下，解本征值问题(2)可以得到模拟站位的模态函数及其一阶导数。图4为S7站位密度和浮力频率剖面以及对应于该背景层结的第一线性模态函数及其一阶导数。该站位5月份的最大浮力频率在9cph左右，分别在20和75m有一个最大值，呈现明显的双跃层结构(见图4(a))。第一模态最大值深度和一阶导数的跨零点均位于140m(见图4(b)，(c))。

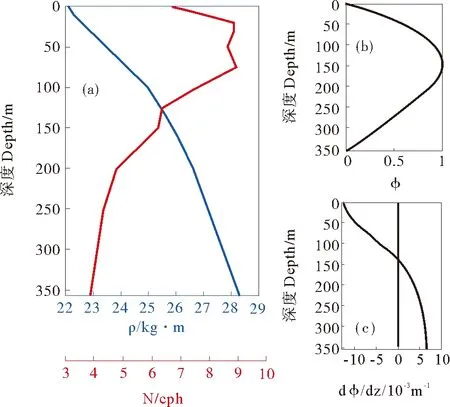
((a) 密度和浮力频率； (b) 模态函数； (c) 模态函数一阶倒数(粗实线)。(a)Densityandbuoyancyfrequency；(b)Modalfunction； (c)Firstderivativeofthemodalfunction(heavysolidline).)

图4S7站位
Fig.4StationS7

2.2.3 模型系数 给定浮力频率，可以由(2)～(6)式分别计算长内波相速度、平方非线性系数、立方非线性系数、频散系数以及地形放大因子等EKdV模型的各个系数。图5为5月份的月平均温盐资料计算的模拟断面各系数沿断面的分布。模拟断面的长内波相速度由起始站位的2.29m·s-1减小到S7站位的1.16m·s-1，其大小主要取决于水深的变化。模拟断面的平方非线性系数均为负值，意味着模拟断面未达到临界深度，即平方非线性系数由负值转变为正值的深度，其绝对值从初始站位的6×10-3s-1增加到103km站位的9.4×10-3s-1，而后逐渐开始减小，到S7站位约减小到7.8×10-3s-1。模拟断面的立方非线性系数均为正值，其量值约比平方非线性系数小两个量级，在88km处达到最大值，约为7.9×10-5m-1·s-1。频散系数的变化与长内波相速度的变化类似，主要取决于水深的变化，其值由深水区的5×105m2·s-1减小到S7站位的6.9×103m2·s-1。放大因子Q主要反映由于地形等因素引起的内孤立波振幅变化，从图5(f)可以看到，在地形变化较缓慢的前80km，放大因子几乎维持在1左右，88km后该值迅速变化，其最大值可达1.2。

2.2.4 模拟结果 进一步的模拟需要确定初始站位的边界(初始)条件。Zhao等[16]通过分析多年的合成孔径雷达(SAR)图像，发现内孤立波在南海北部深水区域大多以单个孤立波的形式存在，其生成途径主要是强内潮的非线性裂变或者强的下陷型扰动的传播。这些单个孤立波向陆架海域传播时进一步裂变，形成了孤立波列，因而在陆架海域观测到的孤立波都是以孤立波列形式存在。Klymak等[1]在南海北部深水区域观测到的内孤立波振幅可达170m，并且与KdV理论波形符合良好。因而，模拟内孤立波由深水向浅水的传播过程可在深水区给出单个KdV型孤立波的边界条件。在初始站位给出如(17)式所示的边界条件，初始振幅为170m的单个KdV型的孤立波，其沿着模拟断面的传播和演变如图6(a)所示。图6(a)时间轴表示以局地长内波相速度运动的坐标系中的时间，即不考虑波动信号从初始站位传播到模拟站位所用的时间，其变换形式已由(14)式给出。从图6(a)中可以清晰地看到内孤立波在每个站位出现的时间和波形的变化。从0～45km，由于非线性系数(绝对值)的增大，初始孤立波振幅逐渐增大，到45km时可达200m左右，且波宽变窄(见图6(b))。45km以后，由于频散和黏性的共同作用，主内孤立波振幅开始衰减，到79km时，其振幅回到170m左右，但此时的波形与初始波形相比其波宽变窄。79km以后，随着水深的变浅，内孤立波逐渐开始裂变，到S7站位，主孤立波的振幅只有60m左右，仅为初始孤立波振幅1/3左右。

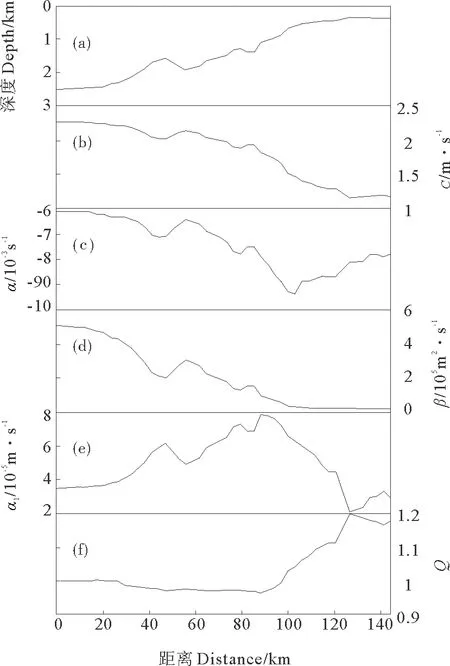
((a)底地形；(b) 长内波相速度；(c) 平方非线性系数； (d) 频散系数； (e)立方非线性系数； (f) 放大因子。(a)Bottomtopography； (b)Longwavephasespeed； (c)Quadraticnonlinearitycoefficient； (d)Dispersioncoefficient； (e)Cubicnonlinearitycoefficient； (f)Amplificationcoefficient.)

图5 模拟断面
Fig.5Thecrosssection

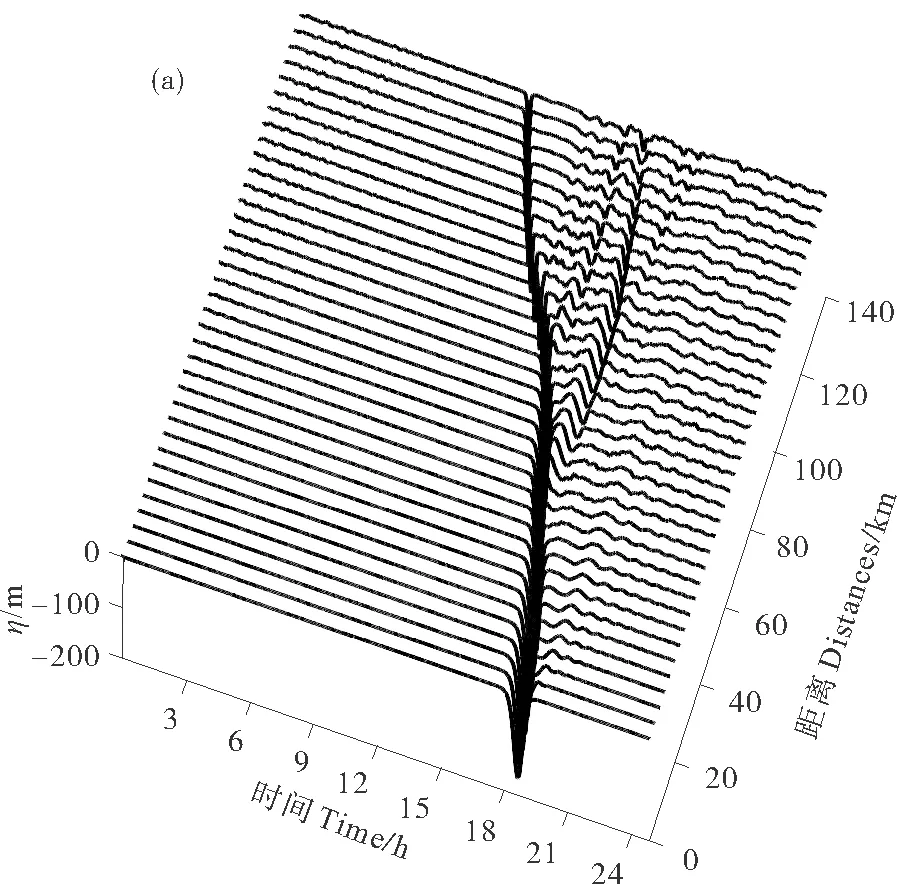
图6(a) 单个大振幅内孤立波沿模拟断面的传播和演变 Fig.6(a) The propagation and evolution of a single large amplitude internal solitary wave along the cross section

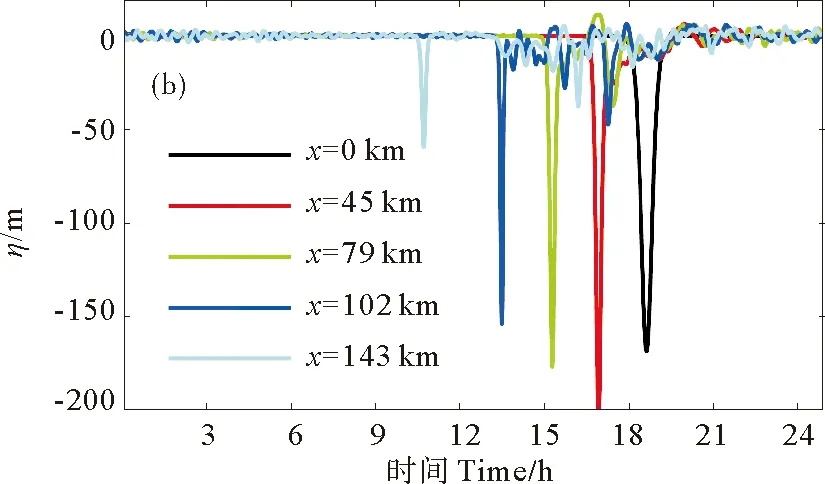
图6(b) 模拟断面上不同站位模拟波形的时间序列Fig.6(b) Time series of wave profile at different locationsalong the cross section

2.3 观测验证

2.3.1 温度 选取S7站位4个典型的孤立波进行验证，其中2个位于第一簇，时间分别为4月25日10时～11时和4月30日10时30分～11时30分。另外2个位于第二簇，时间分别为5月8日7时30分～8时30分和5月12日7时30分～8时30分。从垂向温度振荡看(见图2)，前2个孤立波振幅较小，后2个孤立波振幅较大，均为“a”型内孤立波。理论模型在S7站位的预测结果和S7站位观测等温线的垂直振荡比较如图7所示。图7(a)和7(b)分别为4月25日和4月30日的2个孤立波事件。EKdV理论模型模拟波形从如图6(b)所示S7站位的结果中提取，其未扰动深度为非线性模态函数最大值所在深度(见2.3.2节)。Ramp等[2]根据24度等温线计算的这2个孤立波的振幅均为60m左右，孤立波经过的典型时间跨度约20min。从图7(a)、(b)中可以看到，无论从波形和波宽来看，EKdV理论模型的模拟结果都能很好地符合观测到的内孤立波引起的温度振荡。图7(c)和7(d)分别为5月8日和5月12日的2个孤立波事件，根据24°等温线提取的内孤立波振幅分别为135和95m。如果在浅水区忽略黏性作用(κ从0.001减小为0)，可以在S7站位得到较图6(b)更大振幅的内孤立波，其振幅约为100m。图7(d)的比较结果表明，观测振幅接近100m的内孤立波的波宽和振幅仍然能够很好地用EKdV理论模型的模拟结果来解释。

此外，在图7中同时也给出了连续分层KdV理论模型的模拟结果。与变系数EKdV模型的模拟结果相比，对于振幅大于100m的孤立波(见图7(a)，(b)，(d))，KdV模型与EKdV模型模拟的波宽和振幅是相似的，区别在于最大振幅所在深度。KdV模拟波形最大振幅所在深度对应线性模态函数的最大值所在深度(约为140m)，并且与振幅无关，而EKdV模拟波形最大振幅所在深度对应非线性模态函数的最大值所在深度，随着振幅的增大而减小(见2.3.2节)。对于振幅大于100m的孤立波(见图7(c))，EKdV模拟的振幅约为117m，比KdV模拟的振幅(约92m)更接近观测值(约135m)。

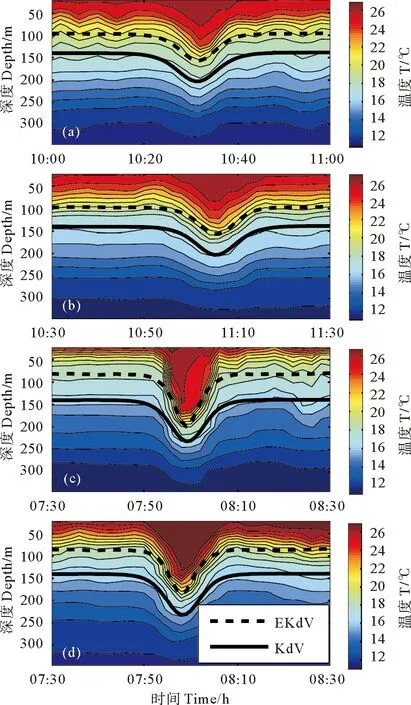
((a) 4月25日；(b) 4月30日； (c) 5月8日； (d) 5月12日。(a)April25； (b)Apr30；(c)May8； (d)May12.)

图7S7站位理论模型模拟波形(粗虚线)和观测等温线振荡的比较
Fig.7Comparisonofthetheoreticalsimulatedwaveprofile(heavydashedline)andtheobservedisothermfluctuationatstationS7

Duda等[17]利用相同的观测结果和典型的KdV波形做过类似的比较，其结果显示，对于大振幅的内孤立波，KdV波形的波宽比实际观测到的内孤立波要窄。Xu等[18-19]比较了利用两层KdV和EKdV模型的环境参数计算的孤立波波形与现场观测孤立波波形的比较，发现EKdV模型的波形更接近实际观测的下凹型孤立波波形。本文用一个考虑了连续分层高阶非线性的理论模型，模拟了单个孤立波从深水到浅水的传播和裂变，得到的波形与实际观测结果相比从波宽上看要好于KdV波形(见图7(d))，且较Duda等[17]的比较结果更具一般性，和Xu等[18-19]的两层模型相比，使用连续分层模型不仅更接近实际海洋层结，而且能够更准确地反映内孤立波模态特征。从图7(c)可以看到，对于振幅更大(例如大于100m)，非线性更强的孤立波，模拟波形与观测相比，波宽较窄，且振幅较小，意味着理论模型在反映强非线性的孤立波方面存在着一定的局限性。

2.3.2 流速 利用理论模型波形的模拟结果，可由(12)、(13)式计算内孤立波引起的水平流速和垂向流速。由于考虑了高阶非线性的作用，需要对线性模态函数进行修正。非线性模态函数的引入使得对于给定振幅的波动，其垂直位移η将变成深度的函数[20]，即对于给定的振幅，非线性模态函数的最大值深度将发生变化，区别于线性模态函数的最大值深度zmax。

不同振幅下，S7站位线性模态函数和非线性模态函数及其一阶导数的垂向结构如图8所示。随着振幅的增大，垂向位移最大值深度逐渐减小，振幅为100m时，该深度由线性模态的140m减小为86m。图7中模拟波形曲线实际上分别代表了非线性模态函数最大值深度上的垂向位移。

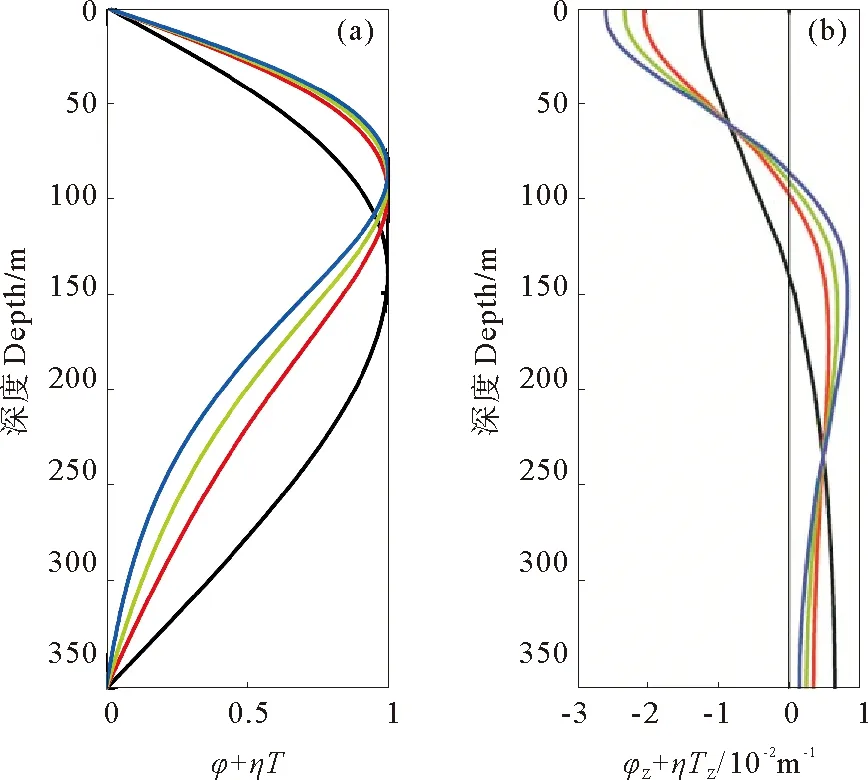
((图中不同颜色粗实线分别表示不同给定振幅：60m(红色)， 80m(绿色)， 100m(蓝色)对应的模态函数。Theheavysolidlineswithdifferentcolorsrepresentdifferentmodalfunctionsforthreegivenamplitudes: 60m(red), 80m(green)and100m(blue),respectively)。(a) 线性模态函数(黑实线)和非线性模态函数；(b) 线性模态函数一阶导数(黑粗实线)和非线性模态函数的一阶导数。(a)Linearmodalfunction(blacksolidline)andnonlinearmodalfunctions；(b)Thefisrtderivativeoflinearmodalfunction(blackheavysolidline)andnonlinearmodalfunctions.)

图8S7站位对应不同振幅的第一模态
Fig.8ThefirstmodefordifferentamplitudesgivenatstationS7

对应于图7中的4个孤立波事件，利用图8给出的模态函数的计算结果，可以分别得到由内孤立波引起的水平流速和垂向流速。由于内孤立波向西传播，波致水平流速主要发生在东西方向，纬向流速分量在水平流速大小中占主要地位。图9给出了这4个孤立波事件发生时，模型计算的水平流速和实测的纬向流速的比较。

孤立波振幅较小(约60m)时，线性模态和非线性模态函数计算的水平流速垂直分布曲线均能较好地反映实测流速的大小和垂直结构(图9(a)、(b))。然而，当孤立波振幅较大(约100m)时，非线性模态函数的计算值与实测的比较有较大的偏差，其计算的最大流速甚至超过2m·s-1。此时，线性模态的计算值与实测的流速结构符合较好，能够准确地反映流速的跨零点。该结果与图7中波形的比较结果有较大差异，波形的比较结果表明，非线性模态较之线性模态能够更准确地反映等温线的垂直振荡。振幅更大(约130m)的孤立波的比较结果显示，非线性模态在反映大振幅内孤立波波致流速结构方面具有更大的偏差，反而，线性模态仍然能够较好地符合流速的垂直结构(见图9(c))。

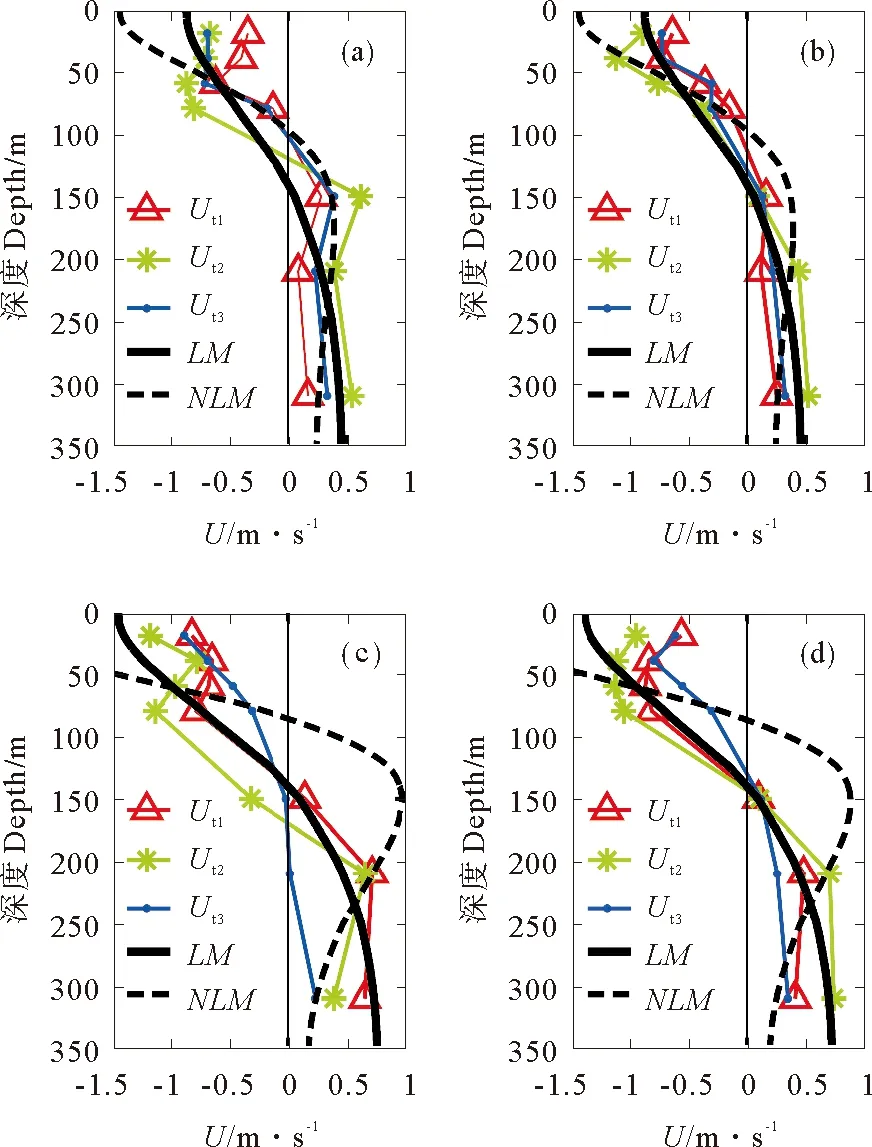
(实测纬向流速分别对应图7中各子图内孤立波引起的等温线振荡；图中各曲线分别表示：内孤立波波峰经过前4min(Ut1)，经过时(Ut2)，经过后4min(Ut3)，线性模态(LM)，非线性模态(NLM) The observed zonal velocity in each subgraph corresponds to the isotherm fluctuation induced by internal solitary wave shown in each subgraph of figure 7; Lines in the figure represent: 4 minutes before the wave crest(Ut1),when the crest passed(Ut2), 4 minutes after the wave crest(Ut3),the linear mode(LM) and the nonlinear mode(NLM), respectively.)

图9 S7站位理论模型计算的水平流速与实测纬向流速的比较
Fig.9 Comparison of the theoretical horizontal velocity and the observed zonal velocity at station S7

3 结论

本文利用变系数EKdV模型模拟了南海北部单个大振幅由深水海域向浅水海域传播和裂变的过程，并且与ASIAEX实验现场观测的温度和流速振荡数据进行了对比，主要得到以下结论：

(1) 变系数EKdV模型能够稳定地模拟单个大振幅强非线性内孤立波向浅水海域的传播和裂变的过程，该过程主要是非线性、频散和黏性效应的平衡；

(2) 变系数EKdV模型能够较好地反映振幅小于100 m的内孤立波的振幅和波宽，对于更大振幅的强非线性内波，该模型模拟的振幅和波宽均较实测较小；非线性第一模态函数能够较准确地体现温度振荡的垂直结构；

(3) 理论模型和波致水平流速的比较结果表明，流速的大小和垂直结构与线性模态较符合，非线性模态在估计由内孤立波尤其是大振幅内孤立波引起的水平流速上存在较大误差。

从理论模型和观测结果的比较来看，变系数EKdV模型能够解释弱非线性的内孤立波以及某些非线性较强的内孤立波，但在解释振幅更大，非线性更强的内孤立波时具有一定的局限性。这一局限性可能源于EKdV理论的局限或者初始波形的选取。尽管如此，变系数EKdV仍然为大振幅内孤立波的传播模拟提供了一个较好的理论手段。

[1] Klymak J M, Pinkel R, Liu C T, et al. Prototypical solitons in the South China Sea [J]. Geophysical Research Letters, 2006, 33(11): L11607.

[2] Ramp S R, Tang T Y, Duda T F, et al. Internal solitons in the Northeastern South China Sea Part I: Sources and deep water propagation [J]. IEEE Journal of Oceanic Engineering, 2004, 29: 1157-1181.

[3] Yang Y J, Tang T Y, Chang M H, et al. Solitons Northeast of Tung-Sha Island During the ASIAEX Pilot Studies [J]. IEEE Journal of Oceanic Engineering, 2004, 29: 1182-1199.

[4] Du T, Yan X H, Duda T. A numerical study on the generation of a distinct type of nonlinear internal wave packet in the South China Sea [J]. Chinese Journal of Oceanology and Limnology, 2010, 28(3): 658-666.

[5] Helfrich K R, Melville W K. Long nonlinear internal waves [J]. Annual Review of Fluid Mechanics, 2006, 38: 395-425.

[6] Fan Z S, Shi X G, Liu A K, et al. Effects of tidal currents on nonlinear internal solitary waves in the South China Sea [J]. Journal of Ocean University of China, 2013, 12(1): 13-22.

[7] Si Z S, Zhang Y L, Fan Z S. A numerical simulation of shear forces and torques exerted by large- amplitude internal solitary waves on a rigid pile in South China Sea [J]. Applied Ocean Research, 2012, 37: 127-132.

[8] Xu Z H, Yin B S, Hou Y J. Response of internal solitary waves to tropical storm Washi in the northwestern South China Sea [J]. Ann Geophys, 2011, 29(11): 2181-2187.

[9] Cai S Q, Xie J S. A propagation model for the internal solitary waves in the northern south china sea [J].Journal of Geophysical Research, 2010, 115(C12): C12074.

[10] Grimshaw R, Pelinovsky E, Talipova T, et al. Internal solitary waves: propagation, deformation and disintegration [J]. Nonlinear Processes in Geophysics, 2010, 17(6): 633-649.

[11] Zhang S W, Fan Z S. Effects of high-order nonlinearity and rotation on the fission of internal solitary waves in the South China Sea [J]. Journal of Hydrodynamics, Ser B, 2013, 25(2): 226-235.

[12] Grimshaw R, Pelinovsky E, Talipova T. Modelling internal solitary waves in the coastal ocean [J]. Surveys in Geophysics, 2007, 28(4): 273-298.

[13] Grimshaw R, Pelinovsky E, Talipova T, et al. Simulation of the transformation of internal solitary waves on oceanic shelves [J]. Journal of Physical Oceanography, 2004, 34(12): 2774-2791.

[14] Holloway P E, Pelinovsky E, Talipova T. A generalized Korteweg-de Vries model of internal tide transformation in the coastal zone [J]. Journal of Geophysical Research: Oceans (1978-2012), 1999, 104(C8): 18333-18350.

[15] Newhall A E, Costello L, Duda T F, et al. Preliminary acoustic and oceanographic observations from the ASIAEX 2001 South China Sea experiment [M]. Woods Hole: Woods Hole Oceanographic Institution, 2001.

[16] Zhao Z, Klemas V, Zheng Q, et al. Remote sensing evidence for baroclinic tide origin of internal solitary waves in the northeastern South China Sea [J]. Geophysical Research Letters, 2004, 31(6): L06302.

[17] Duda T F, Lynch J F, Irish J D, et al. Internal tide and nonlinear internal wave behavior at the continental slope in the Northern South China Sea [J]. IEEE Journal of Oceanic Engineering, 2004, 29: 1125-1150.

[18] Xu Z H, Yin B S, Hou Y J. Highly nonlinear internal solitary waves over the continental shelf of the northwestern South China Sea [J]. Chinese Journal of Oceanology and Limnology, 2010, 28(5)： 1049-1054.

[19] Xu Z H, Yin B S, Yang H W, et al. Depression and elevation internal solitary waves in a two-layer fluid and their forces on cylindrical piles [J]. Chinese Journal of Oceanology and Limnology, 2012, 30(4)： 703-712.

[20] Farmer D, Li Q, Park J H. Internal wave observations in the South China Sea: The role of rotation and non-linearity [J]. Atmosphere-Ocean, 2009, 47(4): 267-280.

责任编辑 庞 旻

Application of Variable-Coefficient Extended KdV Model on the Simulation of Propagation and Disintegration of Internal Solitary Waves in the Northern South China Sea

ZHANG Shan-Wu1， FAN Zhi-Song1， SHI Xin-Gang2

(1.College of Physical and Environmental Oceanography, Ocean University of China, Qingdao 266100, China; 2. China Shipbuiding Information Center, Beijing 100020, China )

A vertical continuously stratified variable-coefficient extended Korteweg-deVries (vEKdV) model is applied to simulate the propagation and disintegration of the large-amplitude internal solitary waves (ISWs) in the northern South China Sea (NSCS), and the results are compared with the observational data. It is found that the vEKdV model fits the wave profile of the observed large amplitude ISWs with amplitude lower than 100m, pretty well, as both the wave amplitude and wave width are consistent with the observed results. However, for the larger ISWs, either wave amplitude or wave width predicted by theoretical model is smaller than in-situ data. The nonlinear modal function can accurately show the vertical structure of temperature fluctuation, while the magnitude and vertical structure of horizontal current are consistent with the linear modal function. The results indicate that the vEKdV model can provide a good theoretical support on the study of propagation and disintegration of large-amplitude ISWs.

internal solitary wave； nonlinear； disintegration； South China Sea

国家自然科学基金重点项目(41030855)资助

2013-11-19；

2013-12-22

张善武(1987-)，男，博士生。E-mail: zhang.shanwu@gmail.com

** 通讯作者： E-mail:fanzhs@hotmail.com

P731.24

A

1672-5174(2015)04-009-09

10.16441/j.cnki.hdxb.20130428