某迭板双向平衡机疲劳寿命分析

姚 涛， 黄朝学

（中国船舶重工集团公司第七一〇研究所，湖北 宜昌 443003）

引言

在现代一些火箭发射装置与多管火箭炮上，大多装设有平衡机，它的作用是对起落部分提供一个推或者拉的作用，从而提供对耳轴的平衡力矩，以平衡起落部分对于耳轴的重力矩。这样，在打高低机进行高低瞄准时，打高时手轮力大为减轻，打低时避免对高低机的撞击；同时有利于瞄准的轻便、平稳，延长了高低机的寿命。

在特定的双向平衡需求前提下，设计了一种迭板扭杆式双向平衡机，并在精心选材的基础上制定了平衡机工艺设计流程，提炼了关键工艺步骤并成功进行了预扭试验，验证了双向平衡方案的可行性。由于该机构将在交变应力状态下工作，根据材料的特性曲线，通过有限元仿真分析对其疲劳寿命进行了预测。疲劳寿命预测结果表明该平衡机满足使用寿命要求。

1 迭板双向平衡机的设计计算

1.1 设计需求

平衡机需要平衡的最大扭矩为4 500N·m，传递到迭板的扭转角度为－37.5°～37.5°。该平衡机按照8万次循环进行理论设计，平衡机结构示意图如图1所示。

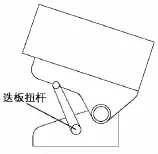
图1 迭板平衡机结构简图

1.2 结构设计

该迭板平衡机主要由迭板、埋头螺钉、垫板、固定套筒及连杆机构等组成。它有左右两个迭板平衡机，其结构完全相同。迭板安装在定向器床上，连杆机构一端与迭板连接，另一端固定在回转盘上。当起落架部分回转时，通过连杆机构带动迭板扭转，从而产生平衡力矩。四片迭板是用埋头螺钉组装，在中间两片迭板的孔与埋头螺钉之间有间隙，埋头螺钉只起连接作用，不提供压力。套筒的方孔通过垫板与迭板上、下面的接触，与迭板侧面有间隙，这便允许迭板扭转时，每片迭板之间可以有相对错动。因此这种端头约束，可视为轻约束，迭板扭转可视为纯扭转，如下页图2所示。

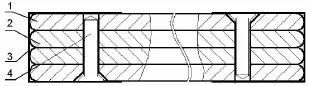
图2 单侧迭板组件

1.3 材料选取

本迭板选材为60Si2CrVA。在对称应力循环下，τ－1的标准对应循环次数为N0＝100万次，根据参考文献［2］，其性能如表1所示。

表1 60Si2CrVA材料性能

1.4 关键工艺与预扭试验

由于迭板平衡机的使用工况要求，对迭板的选材和工艺进行了严格规定。主要有：

1）对毛坯材料进行探伤保证选材结构性能。

2）热处理。（850±20）℃油淬及（410±30）℃回火，从而使其金相组织满足设汁要求。

3）矫直。分两次对迭板进行矫直处理。

设计中迭板组承受双向扭转，受扭段长度为630mm。迭板组在扭转37.5°时承受力矩为4 500N·m，在扭转40°时承受力矩为4 800N·m，随扭角变化，扭力矩的允许公差在5%以内。

对完成加工的迭板试样进行了预扭试验，扭角和扭矩的对应关系曲线如图3所示。该图说明了设计的双向平衡方式方案是可行的。

图3 扭角与扭矩关系拟合曲线图

2 有限元分析

迭板组作为平衡机的执行部件，其自身刚强度与疲劳寿命对平衡机的安全使用起至关重要的作用。考虑到迭板组由四片单迭板组合而成，为方便仿真计算，选择单片迭板进行有限元分析。

2.1 迭板最大切应力计算

在AWE上建立迭板模型，两端分别施加固定约束和角位移，对其静力学分析，结果如图4～7所示。

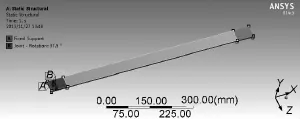
图4 边界条件与载荷

图5 圆周位移云图

图6 最大剪切应力云图

图7 等效应力云图

仿真计算结果总结如表2所示。

表2 单片迭板有限元仿真计算结果

初步分析：由于最大剪切应力为861.8MPa＜900MPa，且最大等效应力为1 577.9MPa＜1 665MPa，故该迭板在工作过程中的静强度是满足使用要求的。

2.2 迭板的疲劳寿命分析

疲劳是引起工程结构和构件失效的最主要的原因之一。通过疲劳分析可以对承受循环载荷作用的零件进行寿命预测，若计算寿命不满足设计寿命，则需改进零件设计尺寸或结构，或选用更好的材料以满足设计寿命要求。

［2－3］中查得，60Si2CrVA 材料的低周和高周疲劳寿命曲线如图8～9所示。

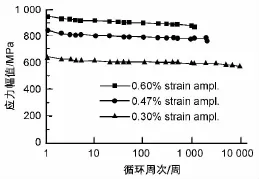
图8 60Si2CrVA低周疲劳寿命S－N曲线

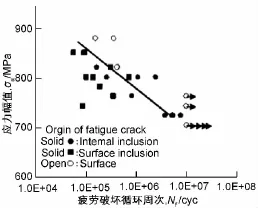
图9 60Si2CrVA高周疲劳寿命S－N曲线

由以上低高周疲劳寿命曲线，读取各循环次数下的应力值，可拟合出60Si2CrVA材料完整的S－N曲线。考虑到迭板的疲劳分析要在AWE中完成，而AWE中所需S－N数据中的S对应的不是单纯的拉伸应力或剪切应力，因此，不能简单的将疲劳试验结果数据作为AWE疲劳分析的输入数据。按照最大剪应力理论公式为σ2＋4τ槡2≤［σ］，其中σ为弯曲正应力，τ为扭转剪切应力，而该迭板基本不受弯曲应力的影响，故上式可近似简化为2τ≤［σ］。鉴于此，将参考文献中查得的各循环次数下的应力值的2倍，作为疲劳分析的输入数据［4］。其数据表格与S－N曲线如图10所示。

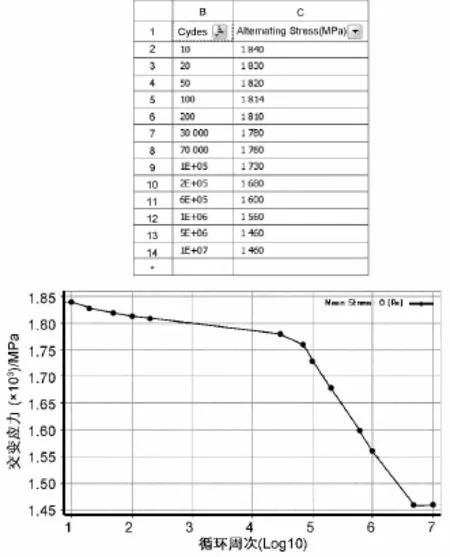
图10 60Si2CrVA材料在AWE中进行疲劳分析所需S－N数据与曲线

在迭板结构有限元分析基础之上，通过添加疲劳工具，并定义相关参数，如疲劳强度因子定义为0.9次，载荷类型选为恒定幅值，由于迭板材料为韧性材料，故平均应力修正理论选择Soderberg修正理论，应力分量选择等效应力，寿命单位为1次循环［5－8］，如图11所示。

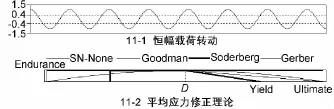
图11 恒幅载荷及Soderberg修正理论曲线

最后，添加寿命结果响应，从而计算出单片迭板的疲劳寿命如图12所示。

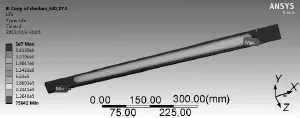
图12 受扭段630mm的单片迭板寿命云图

由以上寿命云图可知，受扭段630mm的单片迭板，在扭转±37.5°的转动位移载荷下，其最小可循环次数为75 842次。

3 结论

1）根据预扭试验，说明采用迭板的双向平衡方式是可行的。

2）由单片迭板的有限元分析可知其静强度满足使用要求。

3）由单迭板的疲劳寿命计算结果可知其最小疲劳寿命值与理论设计值8万次误差为5.2%，说明其仿真结果可靠性高。

4）计算机仿真不仅节省人力物力，同时给设计工作带来启示。疲劳数据随着材料和测试方法的不同而有所变化，所以很重要就是用户要选用能代表自己部件疲劳性能的数据，同时其仿真分析结果的可信度需要试验或者实际使用来验证。

参考文献

［1］ 李军.火箭发射系统设计［M］.北京：国防工业出版社，2008.

［2］ 曾庆祥，何国求，陈成澍.一种高强度钢的低周疲劳特性及其微观机理的研究［J］.西南交通大学学报，1999，34（2）：190－195.

［3］ Weijun HUI，YIhong NIE，Han Dong，et al.High－cycle Fatigue Fracture Behavior of Ultrahigh Strength Steels［J］.J.Mater.Sci.Technol.，2008，24（5）：787－792.

［4］ 单辉祖.材料力学（I）［M］.北京：高等教育出版社，1999.

［5］ 凌桂龙，丁金滨，温正.ANSYS Workbench 13.0从入门到精通［M］.北京：清华大学出版社，2012.

［6］ 李兵，何正嘉，陈雪峰.ANSYS Workbench设计、仿真与优化［M］.北京：清华大学出版社，2008.

［7］ 闻邦春.机械设计手册［M］.北京：机械工业出版社，2011.

［8］ 黄朝学.某扭杆式双向平衡机的设计及疲劳寿命分析［J］.机械设计，2010，27（9）：72－75.