基于单视点调节相机模型的水下图像三维重构

魏迎梅，康来

(1.国防科学技术大学 信息系统与管理学院，长沙 410073;2.国防科学技术大学 信息系统工程重点实验室，长沙 410073)

基于图像的三维重构研究如何从二维(2D)图像中恢复相机参数和三维场景几何信息，该过程是二维成像的逆过程［1］.基于图像的三维重构可分解为相机外参(相机相对姿态)恢复和场景三维结构估计两个部分.假设相机的内部参数已知(现代相机内部参数易于查询)，则可以从图像对应(image correspondences)中获得度量三维重构.基于图像的三维重构基本过程［1］为:首先利用图像匹配技术获取图像对应，然后从图像对应中估计两视图间的本质矩阵，再从本质矩阵中恢复相机相对姿态，最后利用三角化估计场景三维结构.为了进一步提高三维重建质量，可采用梯度下降等非线性优化技术对三维重构结果求精［1］.与传统的手工三维建模方法相比，基于图像的三维重构仅需利用数码相机等廉价设备获取输入数据，而且易于实现自动化处理，具有成本低、操作简单等优势，是计算机视觉中的热门研究内容.作为三维重构的基础，关于相机成像过程及相机模型的研究已经趋于成熟.其中，应用最广泛的是小孔成像模型(或单视点相机模型)，该模型是一种典型的单视点相机模型，即成像过程中所有光线均交汇于一点——相机光心［1］.

水下图像是有别于传统图像的另一类重要图像，由于传统单视点相机模型不能正确描述其成像原理，水下图像三维重构的研究近几年逐渐引起计算机视觉领域的高度关注［2-3］.文献［4］的研究表明，由于水下图像成像过程中，光线传播经过多种折射率不相同的介质，因此水下图像存在折射变形，而且这种变形从理论上来说无法使用径向变形等常见图像变形模型来刻画.因此，传统基于单视点的方法导致水下三维重构结果产生严重的变形［4］.为此，研究人员提出了新的折射相机模型对折射成像过程进行准确的建模，并在此基础上提出了相应的水下图像三维重构方法［3］.但总的来说，基于折射相机模型的基本矩阵计算、三角化及稠密匹配等核心三维重构算法远不及基于单视点相机模型的算法成熟，导致水下三维重构仍然面临较大挑战.现有基于折射相机模型的水下相机标定及三维场景结构计算的效率较低、实用性不够.比如:为了计算两个水下相机的相对姿态，文献［5］的方法耗时以小时计;文献［4，6-8］的方法需要在水下安装已知形状和尺寸的棋盘格标定板，无法实现自动化标定;文献［3］的方法则需要利用运动感应设备获取相机姿态的先验信息.

针对上述问题，本文提出一种基于单视点调节相机模型的水下多视图三维重构方法.具体来说，本文深入分析研究单视点调节模型对水下图像折射变形的补偿能力，在此基础上提出一种高效、自动而且无需标定板的水下图像三维重构方法.此外，通过重构有效性、重构误差等定量指标对本文方法在水下多视图三维重构的性能进行了考察验证.实验结果表明，本文方法可以有效补偿水下图像折射变形，进而提高传统基于单视点相机模型的水下多视图三维重构质量.

1 水下相机及其成像过程建模

1.1 水下相机的构成

一般的水下拍摄系统构成如图1所示.通常将普通相机放在密闭的防护罩内，然后将该装置安装在水下环境，相机透过平面玻璃窗口观察水下场景.在小孔成像模型中(单视点相机模型)，所有场景点对应的光线交汇于一点，即光心.但在水下系统中，由于光线在空气-玻璃以及玻璃-水两个交界面发生折射，因此各场景点对应的光线并不汇聚在相机的中心，水下相机是一种典型的多视点相机.

图1 典型水下相机构成Fig.1 Components of a typical underwater camera

1.2 水下相机成像过程建模

不失一般性，本文分析考察二维情况，并假设折射界面与图像成像平面平行.非平行界面情况下，只需要旋转相机即可.图1所示水下相机二维成像过程如图2所示.相机的中心位于c(0，0).对于场景点xo水下相机模型下的图像点为xa(ra，f)，传统单视点相机下的成像点为xp，下面推导分析xa与xp之间的关系.记光线空气-玻璃折射界面交于xg(rg，zg)(如图2所示)，其坐标分量为

式中:f为相机的焦距;da为相机中心到空气-玻璃折射界面的距离.获得xg后，光线与玻璃-水折射界面的交点 xw(rw，zw)可由 Snell折射定理确定［9］:

式中:na和ng分别为空气和玻璃的折射率;θa和θg分别为xo对应的光线在空气中的部分和在玻璃中的部分与玻璃折射层法线的夹角.式(2)中的三角函数为

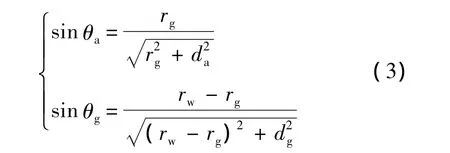
式中:dg为玻璃折射层的厚度.

图2 水下相机成像过程二维示意图Fig.2 2D illustration for imaging process of an underwater camera

联立式(2)与式(3)可得xw的坐标:

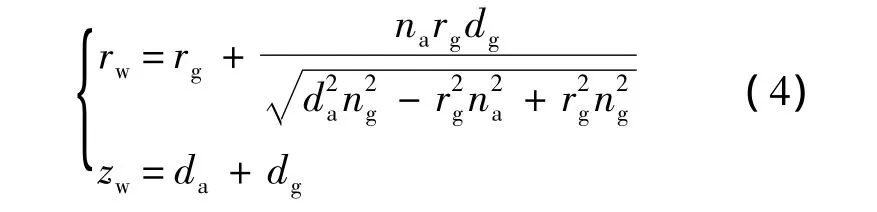
记场景点距离水-玻璃折射界面的距离为dw，获得rw之后进一步计算出场景点ro分量与rw的关系.该过程需要求解方程组:

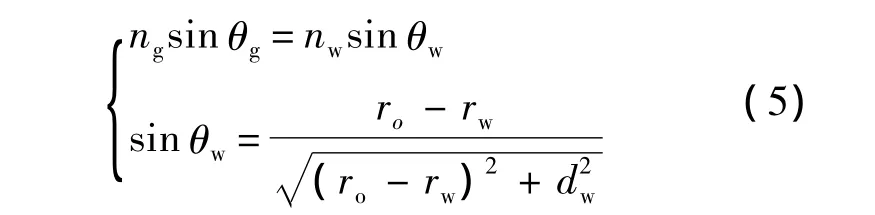
式中:nw为水的折射率，θw为xo对应的光线在水中的部分与玻璃折射层法线的夹角.由式(5)可知，xo的坐标为

其中:

由于在单视点相机模型下，xo在图像平面上的投影为

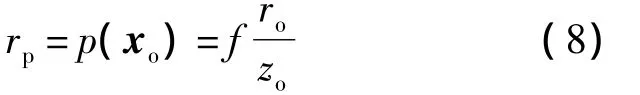
式中:p(xo)为xo的投影函数.

因此，xp最终可以转化为xa，参数向量Θs=［f dadgdwro］T，以及折射率向量 Θn=［nangnw］T的函数.在第 1.2 节中，对于给定的图像点xa，与单视点相机成像相比，二者的差异(即折射变形大小)为

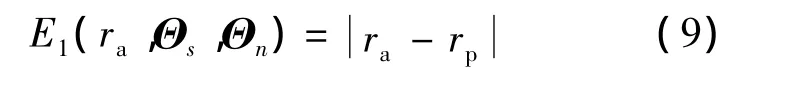
2 单视点调节相机模型及三维重构方法

2.1 单视点调节相机模型折射变形补偿

为了补偿折射变形，本文考察一种单视点调节相机模型，该模型通过同时调节相机的内部参数和外部参数来对折射变形进行描述和补偿.对于内部参数，本文考虑变焦图像空间径向模型.径向变形模型是一种图像空间变形模型，其基本假设［1］是:离图像中心越远的图像点的变形程度越大，而且变形后的图像点与原图像点坐标之间的关系可以采用多项式逼近.本文变焦图像空间径向模型假定水下图像坐标ra与原始未变形图像坐标r'p之间存在简化对应关系［1］:

其中，可调节变量包括相机焦距f，以及调节常系数 k1与 k2，参数向量 Θ's=(f，k1，k2)T共同决定形变补偿的程度.p'(r'p)表示原始未变形坐标r'p的径向变形大小.由式(10)可知.在变焦图像空间径向变形模型下，任意水下图像坐标ra对应的未变形图像点r'p通过求解关于r'p的一元五次方程式(11)来获取.

该模型下的图像变形记为

由于第2.1节变形为图像空间变形，不涉及相机姿态信息的调节.考虑到基于图像的三维重构仅恢复场景的度量信息，而不关注场景的绝对姿态和尺寸，因此本文通过调节相机外部参数来进一步对折射变形进行描述和补偿.外部参数调节基于:对三维场景施加合适的相似变换后，结合镜头镜像畸变矫正和焦距调节，单视点相机模型可以更加准确的近似折射变形，这是使用单视点相机模型获取高精度水下三维重建的前提.实际应用中，由于三维场景的优化不受任何约束，这种近似可能导致三维重建变形，但是从本文后续实验研究表明，这种变形在多视图情形中并不明显.

以二维情形为例，设T2为一个二维相似变换操作，相机姿态调整后，场景点xo的位置变换为

其中，相似变换T2由非零常数因子s、二维旋转矩阵R2以及二维平移向量t2共同决定.在传统单视点相机模型下，施加相似变换后ra对应的未变形图像坐标为

因此，通过内部、外部参数调节后，未能补偿形变量为

为了验证第2.1节折射变形补偿方法的合理性，根据第1.2节水下相机成像过程计算了一个典型配置(f=800，da=100，dg=10，dw=400)下的折射变形及折射变形补偿结果.图3为不同相机模型的折射变形补偿能力，基于单纯变焦径向图像变形模型与本文单视点调节相机模型的补偿结果分别如图3(a)及图3(b)所示.显然，E″远小于因此本文调节相机模型可以取得较好的补偿效果.

图3 不同相机模型的折射变形补偿能力Fig.3 Ability of different cameramodels in compensating for refractive distortion

2.2 水下图像三维重构算法

本节单视点调节相机模型的基础上提出水下图像三维重构算法.由于单视点调节相机模型涉及相机内、外多个参数的调节优化.假定三维场景点的数据量为N，各水下图像点记为ria(1≤i≤N)，本文采用多步优化重建框架:

1)在不考虑变形因素的情况下利用传统三维重构方法［10］获取相机初始内部参数以及场景的初始结构.

2)利用非线性优化调节内部参数，优化目标函数:

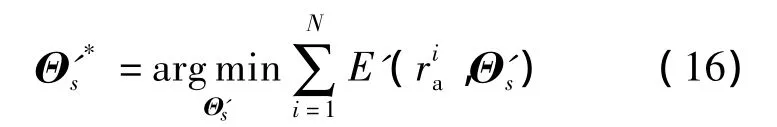
3)利用非线性优化调节外部参数，优化目标函数:

5)考察均方根重投影误差，若大于阈值(本文取0.5像素)，则转至步骤2);否则，输出调解相机模型参数和三维场景结构，结束.

3 实验验证

3.1 实验配置和实验数据

为了对本文方法进行评估，本文采用合成数据和真实图像数据对其进行了定性和定量测试.算法编码实现采用C++语言，非线性优化方法基于开源集束优化(bundle adjustment)实现［11］.本节所有实验均在Microsoft Windows XP操作系统下开展，测试用计算机的处理器为 Intel Core i7-3770 3.4GHz CPU，内存容量为 2GB.

本文方法的性能与如下两种重构方法进行对比:①不采取任何变形补偿方法，直接在传统固定单视点模型下进行重构(记为固定单视点);②利用径向图像变形模型补偿折射变形(记为径向变形).为了确保实验对比的公平性，上述两种对比方法以及本文方法均基于文献［10］提供的框架编码实现，而且系统初始化均只需要指定初始焦距长度(3种方法均采用相同的初始焦距取值).定量实验主要对比分析三维重构结果的有效性和精度.其中，有效性指的是重构的三维场景误差低于某一阈值(本文取场景包围盒最大边长的1%)的三维点所占的比例;精度指的是有效三维场景点的均方根误差.

在实验数据方面，水下合成图像采用光线跟踪算法生成［12］，真实图像通过虚拟相机观察放在水中的3个装饰模型获得.合成数据图像分辨率为640像素 ×480像素，虚拟相机的焦距为600像素，虚拟场景的包围盒长度为1个单位.图4为水下图像数据采集.其中，生成合成数据的装置和合成数据样张分别如图4(a)和图4(b)所示.真实数据图像分辨率为1 032像素×776像素，相机的焦距为1 800像素，分别采用了海螺、古寺、拱门等3个模型(如图4(c)所示).虚拟成像和真实数据采集中，相机排布均呈环状，且相机指向被观察物体.

图4 水下图像数据采集Fig.4 Underwater images data collection

3.2 实验结果与分析

本节首先定性对比重构结果.图5为不同方法在不同输入图像数量条件下的性能比较.其中，图5(a)与图5(b)分别为径向变形方法及本文方法的重构结果(黑色为标准模型，灰色为重构模型).本实验使用的视图数量为16幅.从图5的实验结果可以看出，由于水下图像包含折射变形，因此无法使用径向变形方法来进行多视图三维重构，而本文方法则可对折射进行有效补偿，进而有效消除三维重构结果的变形.注意，固定单视点方法的实验结果与径向变形方法相比，三维重构结果的扭曲程度更加明显，故此处予以省略.

图6为基于合成数据的定量对比实验结果，从有效性(见图6(a))和重建误差(见图6(b))两方面考查不同方法的三维重构性能与输入图像数量之间的关系.实验结果表明本文三维重构方法的性能明显优于传统固定单视点方法和径向变形方法，且使用较多的水下图像可以提升三维重构的精度.

图5 合成水下图像三维重构结果Fig.5 Results of 3D reconstruction using synthetic underwater images

图6 不同方法在不同输入图像数量条件下的性能比较Fig.6 Performance comparison among different methods with varying number of input images

真实图像的定量实验结果如表1所示.本实验使用的视图数量为:海螺、古寺32幅，拱门8幅.由于真实模型的尺寸可以测量，因此重建误差可以mm为单位进行度量.真实图像的定量实验结果如表1所示，表中最优结果加粗显示.表1的实验结果表明，本文单视点调节模型与传统方法相比，可提升三维重构结果的有效性，并可显著降低三维重构误差.上述结论与合成数据的实验结果吻合.

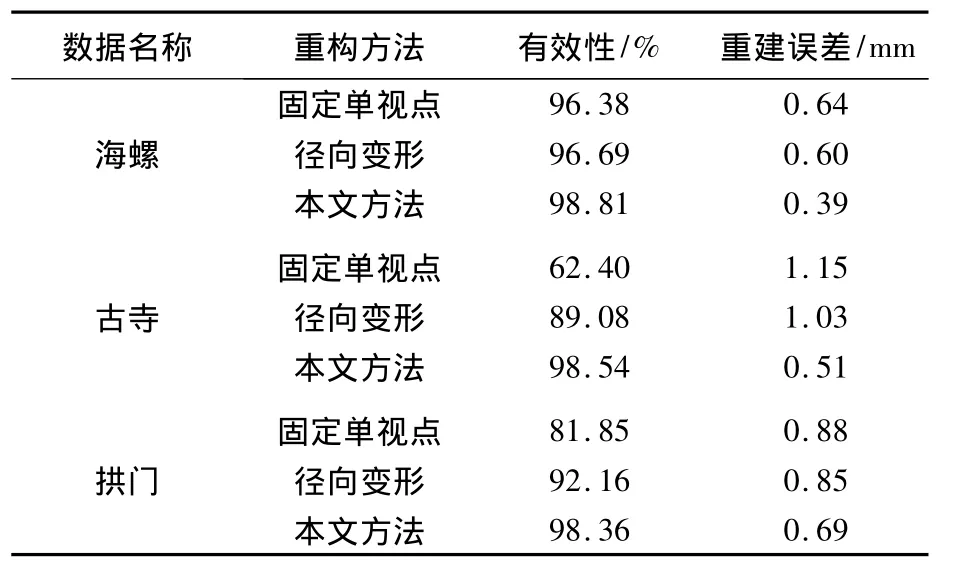
表1 真实图像实验结果对比Table 1 Comparison of experimental results on real images

4 结论

本文基于单视点调节模型的多视图水下三维重构方法可有效补偿折射变形，进而显著提升传统基于单视点相机模型的多视图水下三维重构质量，具有较好的实用性.其优点为:

1)无需安装标定板或其他姿态感应辅助设备，而且算法执行过程可实现自动化.

2)本文所有实验数据单个模型重构过程耗时在10min以内.

本文方法的不足是本文未采用严格的折射相机模型而是采用一种近似相机模型，因此在图像数量较少的情况下重构效果不佳(见图6).

显然，高精度水下图像三维重构是计算机视觉领域的研究热点，相关算法的灵活性和实用性远未达到陆上图像三维重构方法的成熟程度.下一步工作中，拟从水下图像增强、水下相机标定、基于水下图像三维重构的定位与识别等多方面继续开展深入研究.此外，拟采用更加高效的优化方法进一步提升重建效率［13-16］.

References)

［1］ Hartley R，Zisserman A.Multiple view geometry in computer vision［M］.2nd ed.New York:Cambridge University Press，2004:262-276.

［2］ Chari V，Sturm P.Multiple-view geometry of the refractive plane［C］∥ Proceedings of British Machine Vision Conference(BMVC).London:BMVA，2009:1-11.

［3］ Chang Y，Chen T.Multi-view 3D reconstruction for scenes under the refractive plane with known vertical direction［C］∥Proceedings of IEEE International Conference on Computer Vision(ICCV).Piscataway，NJ:IEEE Press，2011:351-358.

［4］ Treibitz T，Schechner Y Y，Singh H.Flat refractive geometry［C］∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition(CVPR).Piscataway，NJ:IEEE Press，2008:1-8.

［5］ Sedlazeck A，Koch R.Calibration of housing parameters for underwater stereo-camera rigs［C］∥ Proceedings of British Machine Vision Conference(BMVC).London:BMVA，2011:1-11.

［6］ Agrawal A，Ramalingam S，Taguchi Y，et al.A theory of multilayer flat refractive geometry［C］∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition(CVPR).Piscataway，NJ:IEEE Press，2012:3346-3353.

［7］ Kunz C，Singh H.Hemispherical refraction and camera calibration in underwater vision［C］∥Proceedings of OCEANS.Piscataway，NJ:IEEE Press，2008:1-7.

［8］ Telem G，Filin S.Photogrammetric modeling of underwater environments［J］.ISPRS Journal of Photogrammetry and Remote Sensing，2010，65(5):433-444.

［9］ Glaeser G，Schrocker H P.Reflections on refractions［J］.Journal for Grometry and Graphics，2000，4(1):1-18.

［10］ Snavely N，Seitz SM，Szeliski R.Modeling the world from internet photo collections［J］.International Journal of Computer Vision，2008，80(2):189-210.

［11］ Triggs B，Mclauchlan P，Hartley R，et al.Bundle adjustment:A modern synthesis［C］∥Vision Algorithms:Theory and Practice，LNCS，2000:298-372.

［12］ NETPLEX.POVRay［EB/OL］.Williamstown，Victoria:Persistence of Vision Raytracer Pty.Ltd.［2015-01-20］.http:∥www.povray.org/.

［13］ Lourakis M IA，Argyros A A.SBA:A software package for generic sparse bundle adjustment［J］.ACM Transactions on Mathematical Software，2009，36(1):1-30.

［14］ Konolige K.Sparse sparse bundle adjustment［C］∥Proceedings of British Machine Vision Conference(BMVC).London:BMVA，2010:1-11.

［15］ Agarwal S，Snavely N，Seitz SM，et al.Bundle adjustment in the large［C］∥Proceedings of European conference on Computer vision(ECCV):Part II.London:Springer-Verlag，2010:29-42.

［16］ Wu C，Agarwal S，Curless B，et al.Multicore bundle adjustment［C］∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition(CVPR).Piscataway，NJ:IEEE Press，2011:3057-3064.