使用对偶分解的MU－CoMP－JT 联合资源分配*

李校林，周 冰，卢 清

(1.重庆邮电大学 通信新技术应用中心，重庆400065;2.重庆信科设计有限公司，重庆400065)

1 引 言

协作多点(Coordinated Multiple－Points，CoMP)技术作为LTE－A 关键技术之一，主要用来扩大高速覆盖区域以及提高边缘用户的频谱效率。CoMP技术又分为协作调度/波束成形(Coordinated Schedulling/Beamforming，CS/CB)和联合处理(Joint Processing，JP)。根据数据信息是否同时由多个传输节点传输，JP 又分为联合传输(Joint Transmission，JT)技术和动态小区选择(Dynamic Cell Selection，DCS)技术，其中JT 技术因其理论上性能增益最好而受到广泛关注，具有重要的研究意义，成为学术界和产业界的研究热点［1］。

CoMP－JT 技术通过基站间的协同发射将干扰变为有用信号，能有效地消除小区间干扰，但多个基站的协同传输改变了网络结构，使得CoMP－JT 的资源分配变得更加复杂［2］。以最大化用户权重速率为目标，文献［3］提出了一种基于SU－CoMP－JT的多小区迭代注水功率分配算法，文献［4］提出了两种基于对角化块编码的注水分配算法，文献［5］提出的多小区合作的MU－MIMO(Multi－User Multiple Input Multiple Output)方案对预编码和功率分配进行了联合优化，文献［6］以最大化用户权重速率为目标推导出了对角化预编码和功率分配的联合优化算法，但这些算法是在给定每个子信道的调度用户集合下进行的，降低了系统的多用户分集增益。为了确定每个子信道的调度用户集合，文献［7］提出了基于SU－CoMP－JT 系统的联合用户选择和边界功率控制的资源分配算法，但考虑的是单载波系统，并不适用于多载波的正交频分多址(Orthogonal Frequency Division Multiple Access，OFDMA)系统，此时CoMP－JT 资源分配需要穷尽搜索每个子信道上可能的用户调度集合，然后利用凸优化方法为每个子信道上的调度用户分配最佳功率。因此，搜索最优解需要极高的复杂度，这使得算法难以适用于多载波CoMP－JT 系统。文献［8］提出的多小区联合预编码和功率控制算法考虑等用户功率分配或等资源块(Resource Block，RB)功率分配，这使得优化问题变成了凸优化问题但一定程度上牺牲了系统性能。以上文献研究目标要么考虑给定每子信道调度用户或者考虑单载波系统，要么考虑等RB 或等用户功率分配，这虽然也能得到最优解但不是全局最优解。文献［9］基于对偶理论将此非凸优化问题分解成多个独立子信道的优化问题，然后通过次梯度迭代法更新拉格朗日因子直至收敛，所求最优解非常接近穷尽最优解，但每个基站并不总是以全功率发送，这是因为为了消除协作簇内同频干扰每根天线在每个子信道上发送功率将受到预编码矩阵的影响，从而导致部分天线不能满功率发送信号。

本文主要研究在CoMP 系统中MU－CoMP－JT的下行资源分配问题，采用迫零(Zero－Forcing，ZF)预编码消除多个小区边缘用户间的同频干扰。在单天线功率约束下以最大化用户权重速率为目标，在多个协作小区间联合优化每个信道上的调度用户、预编码矩阵以及功率分配。本文参考基于对偶分解的多用户OFDM 资源分配算法［10］，在MU－CoMPJT 系统中将联合优化问题分解成多个独立子问题的优化，通过次梯度法更新拉格朗日因子直至目标值最优，其中子问题数量等于发送天线总数。值得注意的是，当子信道上的波束成形流数或接收天线数(以下简称CoMP 模式)小于发射天线数时，采用一种预编码迭代计算方法，该子信道上的发射预编码会随着拉格朗日因子的变化而变化，当算法收敛时每根天线的功率利用率、系统吞吐量将高于现有算法。

2 系统模型与问题描述

2.1 系统模型

考虑N 基站协作簇和M 个用户的下行多小区OFDMA 系统(本文考虑3 基站协作)。基站和用户都配备一根天线，系统带宽为B，子信道数为K，每个小区均采用全频率复用方案，同时协作簇中的基站不仅共享数据信息更共享用户的信道状态信息。假设来自协作簇外的干扰能被有效地消除或设为定值，CoMP 用户m 的接收信号可表示为

用户m 在子信道k 的瞬时速率可表示为

2.2 问题描述

假设每个基站有最大功率约束Pmax，因此基站发送功率满足在任意给定的时隙，N 个基站需要联合决定每个子信道的用户集合s(k)以及s(k)中每个用户的功率分配。考虑到每个子信道上只能存在一种天线协作方式，联合资源分配问题可表示为式(5):

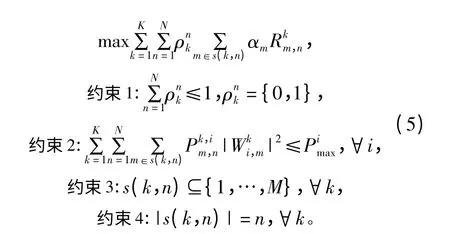
如果CoMP 模式n(即s(k)中有n 个用户时)处于激活状态时，令=1，否则令=0;代 表CoMP 模式n 处于激活状态时子信道k 为用户m 分配的传输速率;αm为用户间的公平性系数。

约束1 保证了每个子载波最多只能分配给一种CoMP 模式，约束2 保证了每天线最大可发送功率，约束3 和4 保证了每一种CoMP 模式的可选用户范围和可选用户总数。除此之外，预编码矩阵还需要满足式(2)约束，从而避免协作簇内的同频干扰。传统的迫零预编码矩阵如下所示:

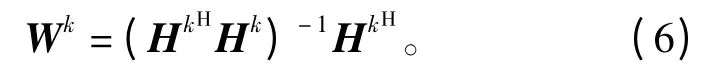
值得注意的是，当收发天线不等时，传统ZF 预编码矩阵会使得每根天线发送功率互不相同，当这些天线的发射功率仅满足总功率约束时性能损失不明显(例如单小区MIMO)，而当这些发射天线分布在不同的地理位置时将受到单天线功率约束(例如多小区CoMP－JT)，因此仅仅使用式(6)所示ZF 预编码矩阵会降低每天线功率使用效率。因此，问题(5)表述的联合资源分配问题还应考虑预编码矩阵的优化。

3 MU－CoMP 联合资源分配算法

如果每个子信道上调度用户集是预定义的，且满足问题(5)中约束3 和约束4，那么问题(5)便成了一个联合功率分配问题。这是一个凸优化问题，因为目标函数是凸函数，且约束1 和约束2 是线性约束，因此它能够通过标准的凸优化方法求解。但一般情况下，问题(5)不是一个凸优化问题，因为它需要为每个子信道寻找最优的调度用户集合，而这是一个联合优化问题。令每个子信道上的用户调度集合数Ψ=M∞/(M－N+1)∞(N－1)∞，从而需要穷尽搜索ΨK种用户调度集合，这便使得问题(5)的最优资源分配需要对每一种用户调度集合情况进行求解，然后从中选出最优分配方式。因此，随着协作小区簇内小区数、子信道数和用户数的增加，穷尽搜索最优解的复杂度会高得难以接受，甚至难以实现。

文献［9－11］中所研究方案考虑了子信道、功率的联合分配问题，但预编码是通过式(6)独立求解，虽然是在总天线发送功率约束下通过注水功率分配能够获得最优吞吐量性能，但不适合单天线功率约束情况。基于此，本节考虑一个联合预编码、功率和子信道资源分配问题。

基于对偶分解理论，通过对式(5)进行对偶分解推导出了一个联合资源分配算法(JRA)。令S 为所有可能的用户配对集合，考虑每个子信道的用户配对情况相同，即考虑在可行域s(k)∈S 内，问题(5)拉格朗日函数为

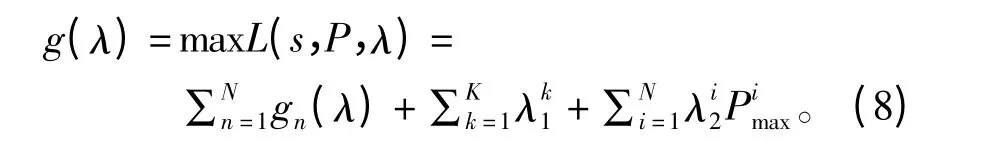
式中，子问题n 可表述为

同理，基于对偶理论，对偶目标函数被分解成n个优化子问题，再将优化子问题分解成K 个子信道的优化问题(简称二级子问题)，如式(10)所示:

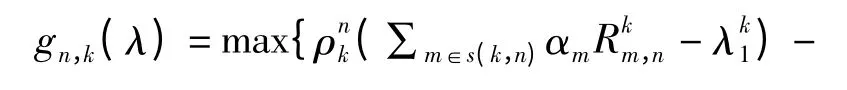
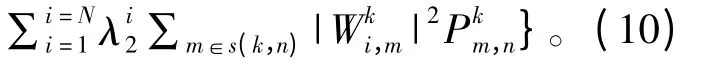
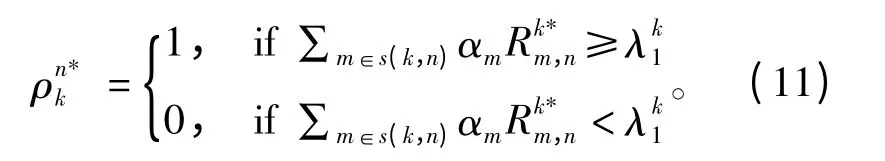
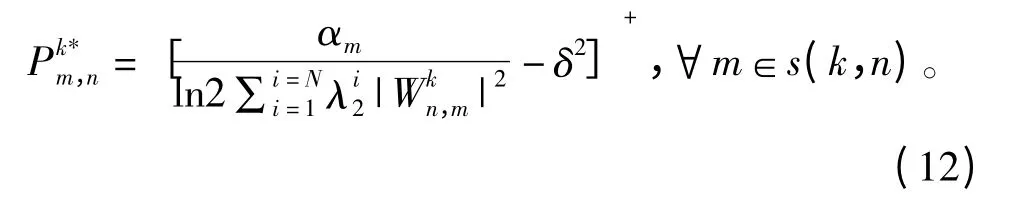
将式(12)代入式(10)可知当

取最小时，能使子载波k 的目标函数值最大。由此可知式(10)中最佳预编码的求解问题可以表示为

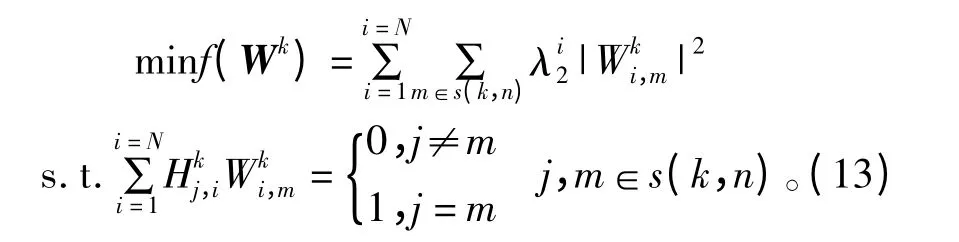
一般而言，当发送天线数N 和接收天线数|s(k，n)|相等时满足式(13)中约束的预编码矩阵唯一，而当发送天线数N 和接收天线数|s(k，n)|不相等时，满足式(13)中约束的预编码矩阵理论上有无穷多个。因此，对于N=|s(k，n)|情况，问题(13)不需要求解，从而仅仅需要考虑N≠|s(k，n)|情况。

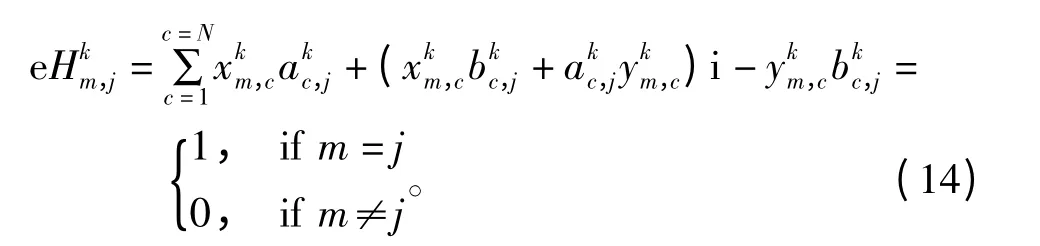
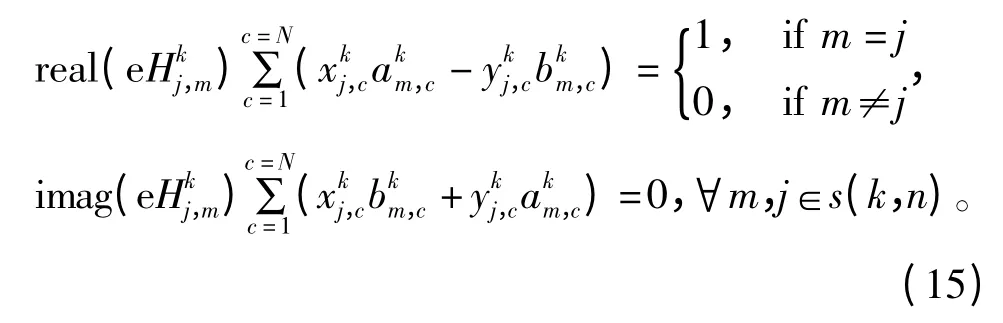
从方程式求解角度可知，方程式(15)有2N 个变量、2|s(k，n)|个方程，当N= |s(k，n)|时，有唯一解;当N ＞|s(k，n)|时显然无解，而这也是MIMO 中最大赋形流数不大于发射天线总数根源所在;当N＜|s(k，n)|时，理论上式(15)有无穷解，利用线性代数相关知识，可轻松求出该无穷解的标准形式(特解+通解)，无穷解中有v=2(N－ |s(k，n)|)个基变量，其余变量是多个基变量复合表达式。因此不妨设和为基变量，令其余变量

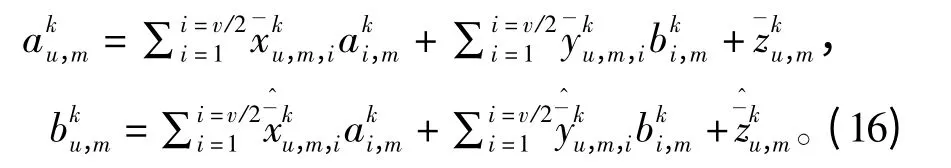
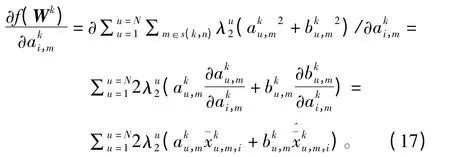
f(Wk)对求二阶导得

f(Wk)对求一阶导得

f(Wk)对求二阶导得

由式(18)、(20)可得，f(Wk)是开口向上的凸函数。显然这是一个凸优化问题，因此当一阶导为零时取最优，即最优解中aki，m和bki，m应满足下式:

3.4 最终分配结果计算

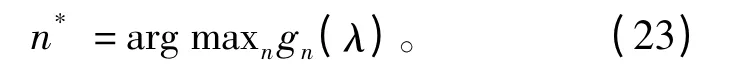
对于变量λk1，令其介于子载波k 上最优和次优之间任意值。对于变量λi2，可通过次梯度算法迭代求得，如下:

为求得问题的最优解，需要通过迭代搜索λk1、直至收敛，其具体流程如图1所示。

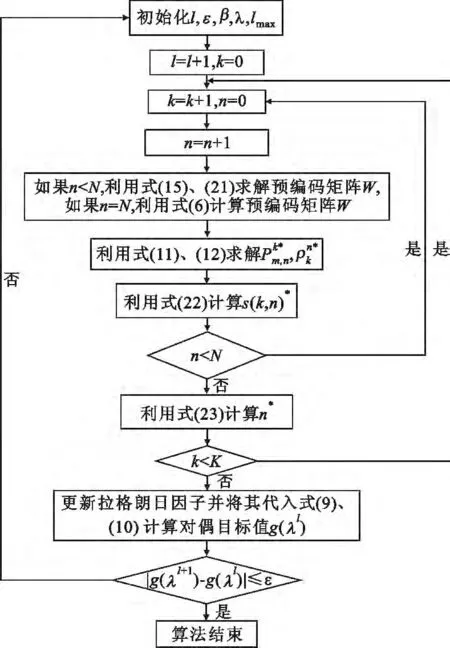
图1 基于对偶分解的MU－CoMP－JT 联合资源分配算法Fig.1 Joint resource allocation algorithm based on dual decomposition for MU－CoMP－JT

4 仿真结果及分析

本文考虑3 小区协同传输的下行OFDMA 蜂窝小区系统，每个子信道带宽为180 kHz，小区半径为500 m。路损模型是PL(d)=128.1 +37.6 lg(d)，单位为dB。阴影衰落服从log－norm(对数正态分布)，均值为零，方差为8。每个子信道的快衰落单独服从瑞利分布。高斯白噪声功率谱密度为－174 dBm/Hz。令γ 表示边缘用户SNR 门限，用户随机分布在小区边缘区域，每个用户速率权重αm为1。设联合资源分配算法在前后两次迭代的对偶目标值的差|g(λl+1)－g(λl)|≤10－4或迭代次数l=300 时停止。仿真中3×2 天线协作模式时每个子信道上有2 个调度用户，而3×3 天线协作时每个子信道上有3 个调度用户。

图2和图3显示了多CoMP 模式的联合预编码优化的资源分配算法(简称MC－JPRA)的收敛性，对比了在不同边缘用户数和不同子信道数时的对偶目标值。对于单CoMP 模式联合资源分配算法(简称SC－JPRA)是MC－JPRA 的特殊情况，因此本文可以通过观察MC－JRA 的收敛性获知SC－JPRA算法的收敛性。拉格朗日对偶变量λ =［1.5，1.5，1.5］，迭代步长β =［0.05，0.05，0.05］。为了验证联合资源分配算法所求解是否足够最优，图2和图3也显示了通过穷尽搜索每个子信道上不同用户配对时的穷尽最优解，可以看出所提MC－JPRA 的对偶目标值呈现单调递减的趋势直到逼近穷尽最优解。对偶间隔随着边缘用户数和子信道数的增加而增加，这是因为计算复杂度会随着边缘用户数和子信道数的增加而增加从而使得对偶间隔增大。

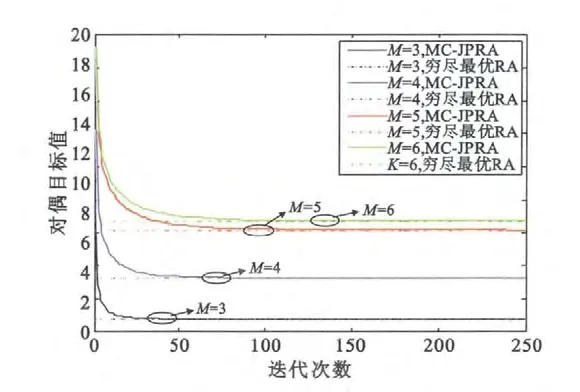
图2 MC－JPRA 算法对偶目标值与迭代次数Fig.2 The dual target versus number of iterations of MC－JPRA

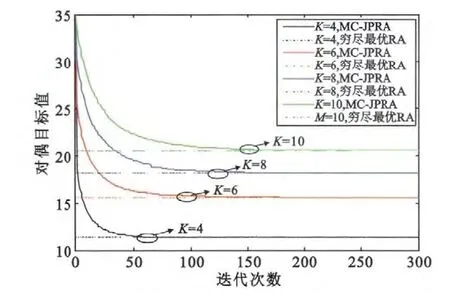
图3 MC－JPRA 算法对偶目标值与迭代次数Fig.3 The dual target versus number of iterations of MC－JPRA

图4和图5比较了单CoMP 模式(SC)和多CoMP 模式(MC)在未考虑预编码优化(JRA)和考虑预编码优化(JPRA)的联合资源分配算法性能。与未考虑预编码优化时相比，不论是在单模CoMP方式(SC－ JPRA)还是多模CoMP 方式(MC－JPRA)，本文所提算法通过联合优化预编码都带来了较大的频谱利用率提升和功率利用率的提升，尤其是当边缘用户SNR 门限值低时，频谱利用率提升更明显，且随着边缘用户SNR 门限的提升系统吞吐量提升比例逐渐降低。

图4 不同模式下JRA 和JPRA 算法的频谱利用率与SNR 变化关系Fig.4 Spectrum utilization versus SNR between JRA and JPRA

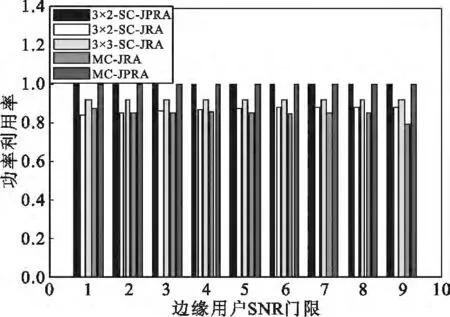
图5 不同模式下JRA 和JPRA 算法的功率利用率与SNR 变化关系Fig.5 Power utilization versus SNR between JRA and JPRA

图6和图7比较了多CoMP 模式在未考虑预编码优化(MC－ JRA)和考虑预编码优化(MC－JPRA)的联合资源分配算法性能。与MC－JRA 相比，图6结果表明所提算法能较大地提升系统吞吐量，且性能增益随着子信道数的增加而增加，但频谱利用率提升速率逐渐降低，这是由于每个子信道的功率降低了。与MC－JRA 相比，图7显示了所提算法能较大地提高频谱利用率，且性能增益随着边缘用户数的增加而增加，这是因为多用户分集增益随着边缘用户数的增加而增加。

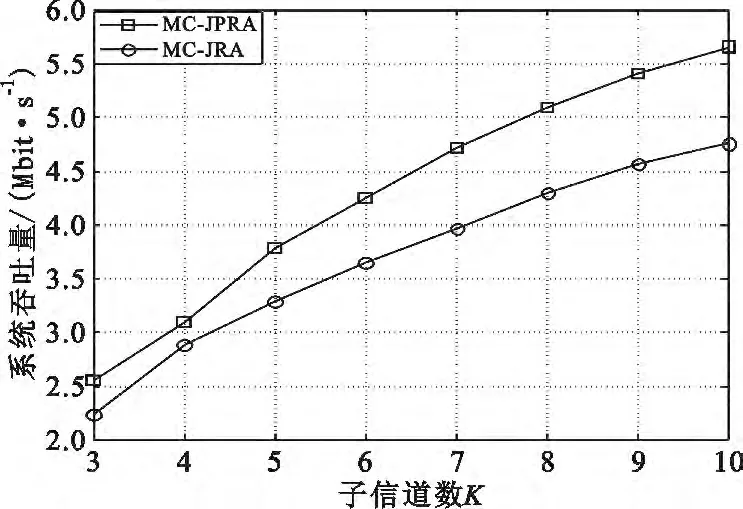
图6 MC－JRA 与MC－JPRA 算法的吞吐量与子信道数的变化关系Fig.6 The throughput versus number of sub－channels between MC－JRA and MC－JPRA

图7 MC－JRA 与MC－JPRA 算法的频谱利用率与边缘用户数的变化关系Fig.7 Spectrum utilization versus edge users between MC－JRA and MC－JPRA

5 结束语

本文提出了一种在多小区OFDMA 系统中的MU－CoMP－JT 联合资源分配算法。采用了一种预编码迭代计算方法，基于对偶理论将复杂的原问题转化为若干个子问题，研究了在多个协作小区和多个子信道间联合优化波束成形流数、用户调度、预编码以及功率分配。仿真结果表明所提算法能够逼近穷尽最优解。与未考虑预编码优化的联合资源分配算法相比，通过联合优化预编码克服了功率利用率不足的缺点，进一步提升了系统吞吐量，有效提高了系统性能，但是算法需要更高的复杂度，因此下一步的工作是研究更低复杂度的联合资源分配算法。

［1］ 3GPP TR 36.814－900，3rd Generation Partnership Project;Technical Specification Group Radio Access Network;Further Advancements for E－UTRA Physical Layer Aspects(Release 9)［S］.

［2］ 卢宪祺，周文安，朱超平.一种基于CoMP 的随机接入方案［J］.电讯技术，2012，52(5):619－623.LU Xianqi，ZHOU Wenan，ZHU Chaoping.A Random Access Scheme Based on CoMP［J］.Telecommunication Engineering，2012，52(5):619－623.(in Chinese)

［3］ Zhang R. Cooperative multi－ cell block diagonalization with per－ base－ station power constraints［J］. IEEE Journal on Selected Areas in Communications，2010，28(9):1435－1445.

［4］ Armada A G，Sánchez－ Fernández M，Corvaja R. Constrained power allocation schemes for coordinated base station transmission using block diagonalization［J］.EURASIP Journal on Wireless Communications and Networking，2011(1):1－14.

［5］ Tolli A，Codreanu M，Juntti M. Cooperative MIMO－OFDM cellular system with soft handover between distributed base station antennas［J］.IEEE Transactions on Wireless Communications，2008，7(4):1428－1440.

［6］ Luo B，Cui Q，Tao X. Constant－Power Joint－Waterfilling for Coordinated Transmission［C］//Proceedings of 2011 IEEE Global Telecommunications Conference.Houston，TX，USA:IEEE，2011:1－6.

［7］ Li J，Svensson T，Botella C，et al. Joint scheduling and power control in coordinated multi－point clusters［C］//Proceedings of 2011 IEEE Vehicular Technology Conference.San Francisco，CA:IEEE，2011:1－5.

［8］ Lakshmana T R，Botella C，Svensson T. Partial joint processing for frequency selective channels［C］// Proceedings of 2010 IEEE 72nd Vehicular Technology Conference Fall.Ottawa，ON:IEEE，2010:1－5.

［9］ Li J，Chen X，Botella C，et al. Resource allocation for OFDMA systems with multi－cell joint transmission［C］// Proceedings of 2012 IEEE 13th International Workshop on Signal Processing Advances in Wireless Communications.Cesme:IEEE，2012:179－183.

［10］ 金慈航.OFDM 系统中基于对偶分解理论的资源分配算法［D］.合肥:中国科学技术大学，2008.JIN Cihang.Resource Allocation Algorithms based on Dual decomposition in OFDM systems［D］.Hefei:University of Science and Technology of China，2008.(in Chinese)

［11］ Yu W，Lui R，Cendrillon R. Dual optimization methods for multiuser orthogonal frequency division multiplex systems［C］// Proceedings of 2004 IEEE Global Telecommunications Conference. Dallas，TX，USA:IEEE，2004:225－229.