一种适用于大数逻辑可译LDPC 码的自适应译码算法*

张 凯，杨 勇

(西安烽火电子科技有限责任公司，西安710075)

1 引 言

低密度奇偶校验(Low Density Parity Check，LDPC)码最早由Gallager 于1963年提出［1］，然而由于当时的硬件条件限制，使得其在提出的30 多年里未得到学者的重视。20世纪90年代后期，由于Turbo码［2］的发现使得学者重新对LDPC 码进行了研究。现在LDPC 码从理论上已被证明是一类非常接近香农限的纠错码［3］。LDPC 码的构造主要可分为两大类，一类是由计算机搜索得到的具有(类)随机特性的LDPC 码［4］，另一类是基于代数性质而得到的具有循环(cyclic)或者准循环(qusi－ cyclic)特性的LDPC 码［5－6］。

LDPC 码的译码算法可分为三类，分别是硬判决译码算法、基于概率域的译码算法和基于可靠度的译码算法。基于可靠度的译码算法主要有大数逻辑译码算法(Iterative Reliability－ Based Majority－Logic Decoding，IRB－MLGD)［7］和基于可靠度的迭代最小和译码算法(Reliability－Based Iterative Min－Sum Decoding，RBI－MSD)［8］。硬判决译码算法主要有一步大数逻辑译码(One－ Step Majority－Logic Decoding，OSMLGD)算法和比特翻转(Bit－flipping，BF)译码算法。基于概率域的译码算法(又称软判决译码算法)所处理的信息采用未经判决的软信息，具有较高的复杂度，常见的算法是和积译码算法(Sum－Product Algorithm，SPA)［9］。为了降低算法复杂度，文献［10－11］详细介绍了SPA 算法，同时将算法中计算双曲正切(tanh)的积转换为寻找最小值，从而大大降低了算法复杂度。虽然软判决译码算法有着最优的译码性能，但是从工程实践的角度来看这种算法存在一定弊端:一方面软判决译码器在译码前需要了解信道的质量，即噪声方差的大小;另一方面修正算法中所引入修正因子的最优数值是与系统中所采用的LDPC 码紧密相关的，最优解通常是由仿真或密度进化(Density Evolution，DE)［12］的方法获得，这无疑限制了LDPC 码在实际中的应用。

针对上述弊端，文献［13］提出了一种基于可靠度的自适应译码算法，其译码性能不依赖于信道的噪声方差。在译码前算法将所有的校验节点根据某种划分准则分为活动(active)节点集合和静态(silent)节点集合，迭代译码的过程中仅活动节点参与信息的交换。然而，这种自适应译码算法的不足之处在于一旦集合划分完毕，算法不会随着迭代译码的演进而自适应改变活动节点集合和静态节点集合。因此这是一种静态的自适应。为了克服这一不足，本文提出了一种动态的自适应译码算法。动态自适应译码算法是一种基于整数可靠度的译码算法，其译码性能不依赖于信道噪声方差，并且在迭代译码的过程中对每个校验节点分别引入不同的自适应修正因子对外信息进行自适应修正。由于节点之间传递的是基于整数的可靠度信息，因此具有低复杂度，十分有利于硬件实现。仿真结果表明，本文提出的动态自适应译码算法的性能与和积译码算法的性能相当。

2 基本概念与符号定义

LDPC 码可以由一个稀疏的奇偶校验矩阵Η=(hi，j)m×n来定义，同时也可以用一个Tanner 图来表示［14］。Tanner 图是一个包含了两种不同节点的二分图，它们分别称为变量节点(variable node)Vj(0≤j ＜n)和校验节点(check node)Ci(0 ≤i ＜m)。其中，变量节点与校验矩阵Η 的列相对应，校验节点与矩阵Η 的行相对应。当对应校验矩阵Η 的元素hi，j为1 时，Tanner 图中第i 个校验点与第j 个变量点相连。对于任意LDPC 码的校验矩阵，定义如下两个下标集合:

对矩阵Η 中的每一行i，定义

Ni={j:0≤j≤n－1，hi，j=1};

对矩阵Η 中的每一列j，定义

Mj={i:0≤i≤m－1，hi，j=1}。

3 自适应RBI－MSD 译码算法

LDPC 译码算法中通常会引入一个修正因子来修正变量或校验节点所接收的信息，例如偏移/归一化的BP 算法和RBI－MSD 算法。一般地，这个修正因子的数值在迭代的过程中恒定不变。为了实现自适应译码算法，不同的校验节点应该具有不同的修正因子，且修正因子的数值应随着迭代次数的增加而动态改变。下面分别介绍自适应译码算法在变量节点和校验节点主要的计算。

(1)变量节点:每个变量节点将与其相连的校验节点传送来的信息作为输入信息进行处理，并将处理后的外信息(extrinsic message)回传至相应的校验节点。

(2)校验节点:第i 个校验节点将与其相连的变量节点传送来的信息作为输入信息进行处理，并用修正因子α(k)i将外信息进行修正，而后回传至相应的变量节点。其中，符号α(k)i表示在第k 次迭代过程中第i 个校验节点的修正因子。显然，自适应译码算法的性能极大地依赖于自适应修正因子α(k)i。本文的主要工作就是在不牺牲译码性能的前提下，给出自适应因子的选取准则。方便起见，我们以RBI－MSD 算法为例给出自适应RBI－ MSD 译码算法。

令c=(c0，c1，…，cn－1)是待传送的码字向量。假设采用的调制方式为BPSK，则调制后的向量为x=(x0，x1，…，xn－1)，其中xi=2ci－1。经高斯信道叠加噪声后得到向量y =(y0，y1，…，yn－1)。为了降低算法的复杂度和计算量，我们令不同节点之间交换的信息都是整数的可靠度信息。因此，在接收端需要将接收到的实数信息进行量化，使其转换成整数化的可靠度信息。

令Δ ＞0、b ＞1 是在量化过程中需要用到的两个参数，其中Δ 是量化区间间隔长度，b 是量化比特位数。接收到的数值yj(0≤j ＜n)经截断处理后被均匀量化到间隔为Δ 的2b－1 个小区间中的某个区间，每个区间可以用b 个比特来表示。假设量化后的序列为q=(q0，q1，…，qn－1)，其中qj是一个取值在［－(2b－1)，+(2b－1)］范围内的整数。这里需要说明的是，在量化的过程中，凡是超过量化范围的接收值，一律进行截断处理。也就是说，如果超出量化范围，那么就令|qj| =(2b－1)。接收值yj(0≤j ＜n)的量化函数定义如下:

式中，符号［x］表示将数值x 向0 方向取整。直观地讲，接收信号的幅度越大，量化结果的绝对值也越大。因此，量化值qj能够反比特信息的可信度。

(2)校验节点信息处理:校验节点Ci(0≤i ＜m)接收到与其相连的变量节点发送的信息，则从校验节点Ci(0≤i ＜m)向变量节点Vj传送的外信息计算如下:

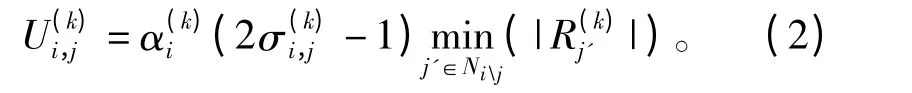
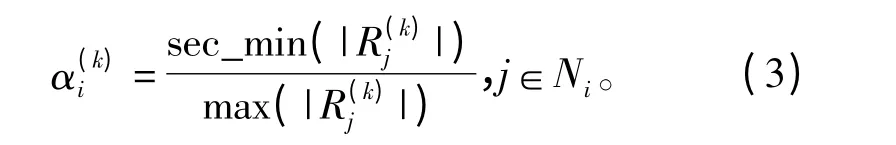
式中，符号sec_min(x)表示向量x 中次小的数值。

(3)变量节点信息处理:变量节点Vj(0≤j ＜n)的和外信息(total extrinsic information)计算如下:

用于变量节点信息更新的准则为

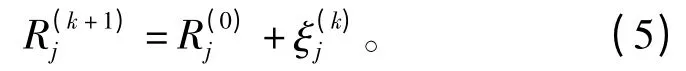
并将更新后的可靠度传送给与其相连的校验节点。

基于上述三个主要步骤，我们可以将自适应RBI－MSD 译码算法归纳如下:

Step 1 输入:接收向量y，量化函数参数Δ、b 和译码最大迭代次数Imax;

Step 2 初始化:根据式(1)将接收向量y 量化为整数可靠度向量q;设置迭代次数标识k=0;设置初始可靠度信息R(0)j=qj(0≤j ＜n);

Step 3 迭代:当k ＜Imax时，执行以下步骤:

(3)对于每个校验节点Ci(0≤i ＜m)，根据式(3)得到自适应修正因子，并根据式(2)计算传送至变量节点的外信息;

(5)对于每个变量节点Vj(0 ≤j ＜n)，根据式(5)更新其可靠度信息，并将更新后的可靠度信息传送至相邻的变量节点;

(6)迭代次数标识k=k+1;

Step 4 输出:将硬判决向量z(k)作为译码器的输出。

为了更加清楚地说明自适应RBI－MSD 译码算法的流程，图1给出了算法流程图。

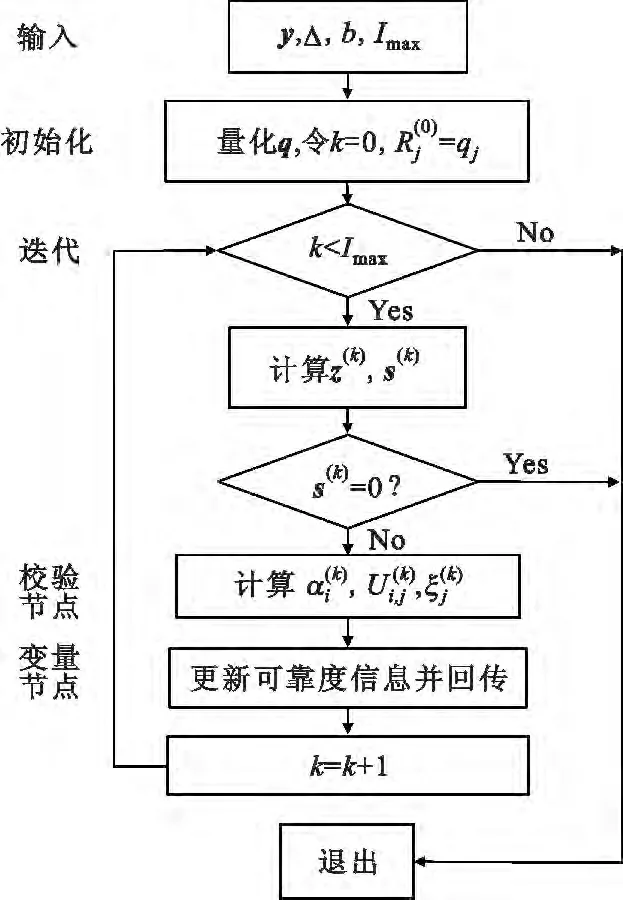
图1 自适应RBI－MSD 译码算法流程图Fig.1 Flow chart of the adaptive RBI_MSD decoding algorithm

4 性能仿真与分析

4.1 仿真实验1

考虑一个基于有限域特性构造的(961，721)规则QC－LDPC 码［6］，它是大数逻辑可译码，对应的校验矩阵Η 的行数与列数都是961，其行重和列重均为30。为了比较算法之间的性能，仿真的量化参数与文献［8］中设置的一致，Δ =1/64，b =8，原始RBI－MSD 算法的修正系数为0.25。最大迭代次数设置为50，传输信道为高斯信道，调制方式为二进制相移键控(Binary－ Phase－ Shift－ Key，BPSK)。仿真结果如图2和图3所示，为了便于比较不同算法之间的性能，图中同时给出了原始RBI－MSD 译码算法和SPA 译码算法的性能高曲线。

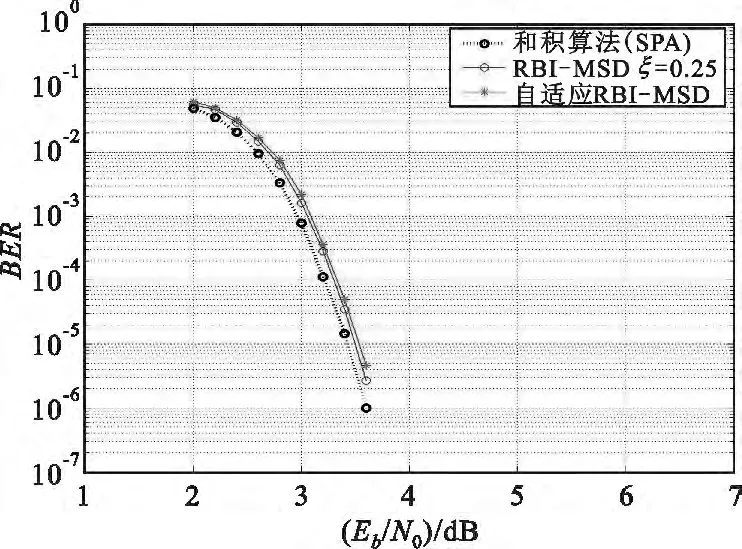
图2 (961，721)自适应译码算法性能曲线Fig.2 Error performances of the(961，721)

图3 (961，721)自适应译码算法迭代次数Fig.3 Average iteration number of the(961，721)

从图2和图3中可以看到:

(1)自适应RBI－MSD 算法的译码性能非常接近SPA 算法的译码性能;

(2)结合自适应修正因子，自适应RBI－ MSD算法的性能相比于原始RBI－MSD 算法的性能基本无损耗;

(3)自适应RBI－MSD 算法的收敛速度与原始RBI－MSD 算法的收敛速度相当。例如，在Eb/N0=4.0 dB时，原始RBI－MSD 算法和自适应RBI－MSD算法的平均迭代次数分别为2.123 和2.567 次。

4.2 仿真实验2

考虑一个基于有限几何特性构造的(4095，3367)规则循环LDPC 码［5］。对应的校验矩阵Η 的行数与列数都是4095，其行重和列重均为64。其余参数设置同仿真1。

仿真结果如图4和图5所示，为了便于比较不同算法之间的性能，图中同时给出了原始RBI－MSD 译码算法和SPA 译码算法的性能曲线。

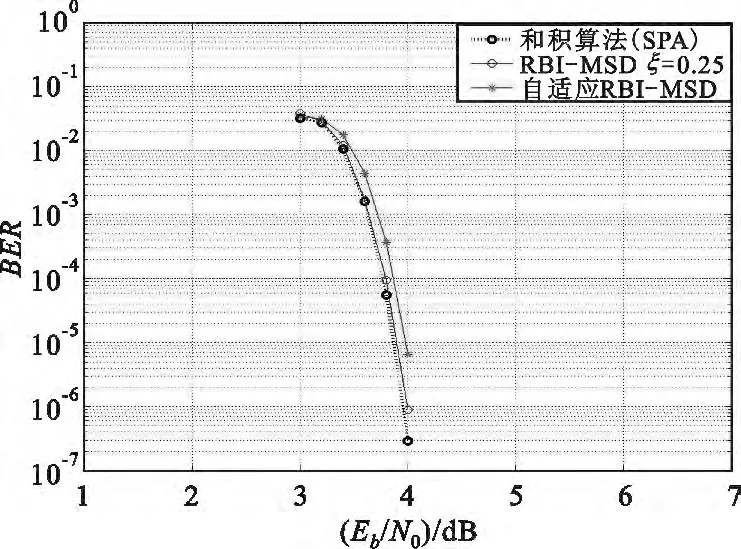
图4 (4095，3367)自适应译码算法性能曲线Fig.4 Error performances of the(4095，3367)

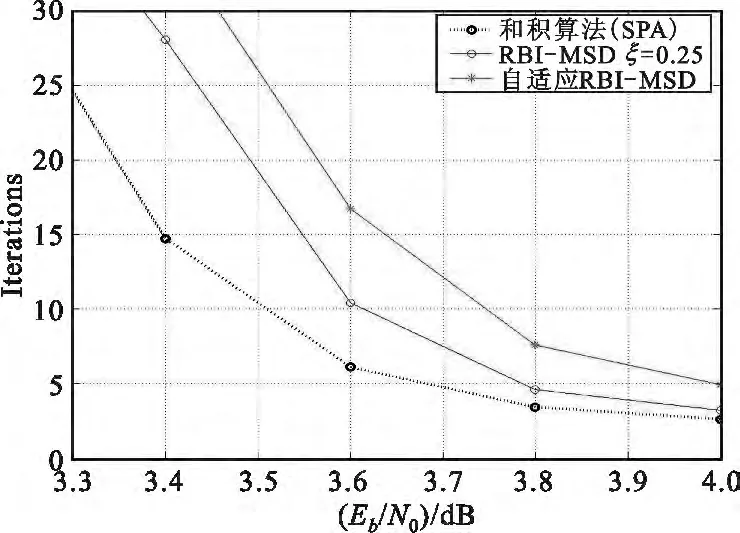
图5 (4095，3367)自适应译码算法迭代次数曲线Fig.5 Average iteration number of the(4095，3367)

从图4和图5中可以看到:

(1)自适应RBI－MSD 译码算法的性能非常接近于SPA 算法和原始RBI－MSD 译码算法。例如，在误码率BER=10－5时自适应RBI－MSD 译码算法的性能与SPA 算法的性能之间仅有0.1 dB;

(2)自适应RBI－MSD 算法的收敛速度与原始RBI－MSD 算法的收敛速度相当。例如，在Eb/N0=4.0 dB时，原始RBI－MSD 算法和自适应RBI－MSD 算法的平均迭代次数分别为3.23 和4.92 次。

5 结 论

本文给出了适用于大数逻辑可译LDPC 码的自适应准则，并以RBI－MSD 算法为例详细描述了自适应RBI－MSD 译码算法。原算法中对每个校验节点引入相同的修正因子，而在自适算法中对每个校验节点分别引入了不同的自适应修正因子来修正校验节点发送的外信息，其中修正因子通过算法自适应获得。通过对基于有限域特性和有限几何特性构造出的不同类型的大数逻辑可译LDPC 码进行译码，可以看到自适应RBI－MSD 译码算法对于大数逻辑可译LDPC 码的普适性。提出的自适应算法具有复杂度低、可并行运算、全整数的信息传递等优点，十分有利于工程实现。同时，该自适应译码算法也为快速、高效、可靠的译码奠定了理论基础，更为今后该方面课题的研究提供了借鉴。

［1］ Gallager R G. Low－ density parity－ check codes［M］.Cambridge:MIT Press，1963.

［2］ 肖创创，郭荣海，李际平，等. 直升机卫星通信系统中Turbo 码外交织器设计与仿真［J］.电讯技术，2014，54(4):486－490.XIAO Chuangchuang，GUO Ronghai，LI Jiping，et al. Design and Simulation of Turbo Codes Interleaver in Helicopter Communication System［J］. Telecommunication Engineering，2014，54(4):486－490.(in Chinese)

［3］ Richardson T，Shokrollahi A，Urbanke R.Design of capacity－approaching low－density parity－check codes［J］.IEEE Transactions on Information Theory，2001，47(2):619－637.

［4］ Hu X Y，Eleftheriou E，Arnold D. Regular and irregular progressive edge－growth tanner graphs［J］.IEEE Transactions on Information Theory，2005，51(1):386－398.

［5］ Kou Y，Lin S，Fossorier M P C. Low－ density parity－check codes based on finite geometries:A discovery and new results［J］. IEEE Transactions on Information Theory，2001，47(7):2711－2736.

［6］ Lan L，Zeng L Q，Tai Y，et al.Construction of quasi－cyclic LDPC codes for AWGN and binary erasure channels:a finite field approach［J］.IEEE Transactions on Information Theory，2007，53(7):2429－2458.

［7］ Huang Q，Kang J Y，Zhang L，et al.Two reliability－based iterative majority－ logic decoding algorithms for LDPC codes［J］. IEEE Transactions on Communications，2009，57(12):3597－3606.

［8］ Chen H，Zhang K，Ma X，et al.Comparisons between reliability－based iterative min－sum and majority logic decoding algorithms for LDPC codes［J］.IEEE Transactions on Communications，2011，59(7):1766－1771.

［9］ Kschischang F R，Frey B J，Loeliger H A. Factor graphs and the sum－ product algorithm［J］. IEEE Transactions on Information Theory，2001，47(2):498－519.

［10］ Wiberg N，Loeliger H A，Kotter R. Codes and iterative decoding on general graphs［J］. Eoropean Transactions on Telecommunications，1995，35(6):513－526.

［11］ Chen J，Dholakia A，Eleftheriou E.Reduced－complexity decoding of LDPC codes［J］. IEEE Transactions on Communications，2005，53(8):1288－1299.

［12］ Richardson T，Urbanke R. The capacity of low density parity－check codes under message－passing decoding［J］.IEEE Transactions on Information Theory，2001，47(2):599－618.

［13］ Zhang K，Chen H，Ma X. Adaptive decoding algorithms for LDPC codes with redundant check nodes［C］//Proceedings of 2012 International Symposium on Turbo Codes and Iterative Information Processing.Gothenburg，Sweden:IEEE，2012:175－179.

［14］ Tanner R M. A recursive approach to low complexity codes［J］. IEEE Transactions on Information Theory，1981，27(5):533－547.