芋头浆的流变特性
2015-03-17余振宇姜绍通潘丽军戴缘缘吕侠影
余振宇,姜绍通*,潘丽军,戴缘缘,吕侠影
(合肥工业大学生物与食品工程学院,农产品加工研究院,安徽省农产品精深加工重点实验室,安徽 合肥 230009)
芋头浆的流变特性
余振宇,姜绍通*,潘丽军,戴缘缘,吕侠影
(合肥工业大学生物与食品工程学院,农产品加工研究院,安徽省农产品精深加工重点实验室,安徽 合肥 230009)
摘 要:研究不同质量分数芋头浆在不同温度下的流变学性质。静态流变性质测定结果表明:在研究的质量分数(10%~30%)和温度(0~80 ℃)范围内,芋头浆是具有假塑性的非牛顿流体,其流变特性服从Herschel-Bulkley模型;随着质量分数的增大,芋头浆的非牛顿性在 逐渐增强,浆体的屈服应力和黏稠系数逐渐增大,流变特性指数逐渐减小;随着温度的升高,芋头浆的表观黏度不断降低,浆体的非牛顿性逐渐减弱,黏稠系数逐渐减小,流变特性指数逐渐增大,温度与芋头浆黏稠系数的关系可用Arrhenius方程进行拟合;动态流变性质测定结果表明:芋头浆显示弱凝胶特性。
关键词:芋头浆;流变特性;Herschel-Bulkley模型;凝胶特性
芋头含有丰富的淀粉、蛋白质、维生素和矿物质元素,可食用也可药用,具有宽肠胃、补脾胃、降脂、降血压、消痨散结等功效,芋头中富含的多糖还有具有增强细胞免疫和体液免疫的功能[1-2]。我国的芋头品种丰富、种植面积广泛,但其开发程度远不及山药、甘薯、马铃薯等,由于在收获和贮存期间的继续代谢、损伤、腐烂、皱缩和发芽而遭受采后损失,只有一部分被食用,造成了很大的浪费[3]。所以对芋头进行深入开发具有重要意义。
目前市场上有关芋头的深加工产品并不多,主要有芋头泥、芋头全粉、芋头冰淇淋、芋头冷冻食品等固体或半固体类产品[4-7],液体类饮料的开发更是鲜有报道。因此,以芋头为原料,开发一款具有低脂、高膳食纤维特点的芋头浆体饮料,可最大限度地保持芋头的营养价值和独特风味。芋头饮料的开发,不仅可以增加现代方便食品的花色品种,也为芋头的深加工开辟了一条途径,对芋头产业的发展具有深远意义。
流变性是食品所表现出来的黏性流体力学和弹性力学的性质,对食品的运输、传送、加工工艺以及咀嚼食品时的满足感都起着非常重要的作用[8]。近年来,果蔬汁等液态食品流变特性研究较为广泛,许多学者对香蕉浆、番茄浆、浓缩蓝莓汁、浓缩芒果汁等浆体的流变特性进行研究,这些浆体体系都表现为Herschel-Bulkley流体模型[9-12]。芋头浆是制备芋头饮料的基本物料,其流变特性的研究为芋头饮料的配方、加工工艺设计提供理论基础,也为工业化生产中加工设备选型、物料运输中能量损耗、产品质量控制、包装等提供依据[13]。本实验对芋头浆的流变性质进行研究,研究芋头浆的流体类型以及流变参数随质量分数、温度的变化规律。这些对于提高芋头饮料的加工质量,生产不同要求的产品,调节生产工艺过程都具有一定指导意义。
1 材料与方法
1.1材料与仪器
新鲜莱阳芋头:购于合肥家乐福超市,芋头块茎中的水分含量为82.88%。
FK-A组织捣碎机 江苏金坛市金城国盛实验仪器厂;DHR-3型流变仪 美国TA公司。
1.2方法
1.2.1 芋头浆的制备
将新鲜的芋头蒸煮熟化后去皮,分别按照芋头终质量分数10%、15%、20%、25%、30%加入蒸馏水,通过组织捣碎机进行打浆,即制得芋头浆。
1.2.2 静态流变性质测定
质量分数对芋头浆流变性的影响测定:采用40 mm平行板测量系统,两平板之间的距离为1 000 μm,在20 ℃条件下测定不同质量分数样品(10%、15%、20%、25%、30%)表观黏度和剪切应力随剪切速率(0~300 s-1)的变化曲线,再对不同质量分数芋头浆的流变曲线进行拟合,得出芋头浆的流变模型及其流变特性参数。
温度对芋头浆流变性的影响测定:固定剪切速率在1 s-1,在10~50 ℃条件下测定不同质量分数芋头浆表观黏度随温度的变化曲线;配制质量分数为15%的芋头浆,分别测定样品在0、20、40、60、80 ℃条件下的剪切应力随剪切速率的变化曲线,并对其流变特性曲线进行拟合,得到质量分数15%芋头浆在不同温度条件下的流变模型及流变特性参数。
1.2.3 动态流变性质测定
线性黏弹区的确定:采用动态法测定流体的流变性质,首先需要确定流体的线性黏弹区。采用40 mm平行板测量系统,测定温度为20 ℃,振荡频率固定在1 Hz,测定复合模量G*随振荡应变的变化,复合模量G*恒定的振荡应变区即为芋头浆的线性黏弹区。
频率扫描:在线性黏弹区内对芋头浆进行频率扫描,振荡应变固定在0.5%,振 荡频率范围为0.01~2 Hz。测定频率扫描过程中贮能模量G’、耗能模量G’以及动力学黏度η’的变化。
1.3数据统计分析
采用Origin8.0软件对实验数据进行分析和作图。
2 结果与分析
2.1芋头浆静态流变性质
2.1.1 不同质量分数芋头浆的流变特性
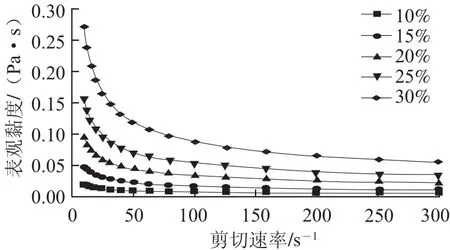
图1 不同质量分数芋头浆表观黏度随剪切速率的变化曲线Fig.1 Relationship between shear rate and apparent viscosity of taro pulp at different concentrations
由图1可知,在剪切速率一定的情况下,芋头浆的表观黏度随着质量分数的增加而增大,当剪切速率较小时,这种增大的趋势更加明显。此外,在研究的质量分数范围内,芋头浆的表观黏度也随着剪切速率的增加而逐渐减小,表现出剪切变稀的假塑性流体特征。这是因为芋头浆在静止或者低剪切速率的情况下,浆体中的淀粉等链状高分子之间相互连结、缠绕,形成了三维网状结构,增加了分子之间的作用力,浆体从而表现为高黏度性质[8]。当剪切速率增加时,浆体中聚集或缠绕在一起的淀粉等链状高分子会发生解体或变形,分子之间形成的网络结构被破坏,降低了流体阻力,从而使芋头浆的表观黏度减小,呈现出剪切稀化的现象[14]。芋头浆剪切稀化的性质有利于其在加工过程中的泵送和灌注。
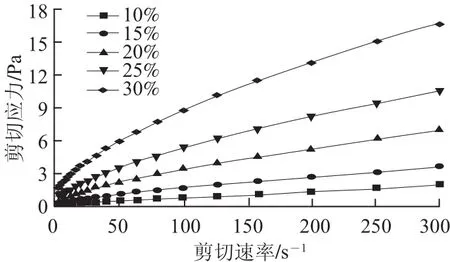
图2 不同质量分数芋头浆剪切应力随剪切速率的变化曲线Fig.2 Relationship between shear rate and shear stress of taro pulp at different concentrations
由图2可知,不同质量分数芋头浆的剪切应力随着剪切速率的增加而增大,这是由于当剪切速率增加,浆体的流速增加,速率梯度增大,要破坏体系中缠绕在一起的淀粉颗粒等固形物使其解体或变形,剪切力也会随之增大[15]。
质量分数为10%~30%的芋头浆均呈现典型的屈服-假塑性流体特性行为,这些曲线可采用Herschel-Bulkley模型τ=τ0+kγn进行拟合,式中:τ0为屈服应力/Pa,k为黏稠系数/(Pa·sn),γ为剪切速率/s−1,n是流变特性指数,得到的拟合参数见表1;对芋头浆的黏稠系数k和流变特性指数n与质量分数的数学关系进行拟合,所得曲线和方程见图3。
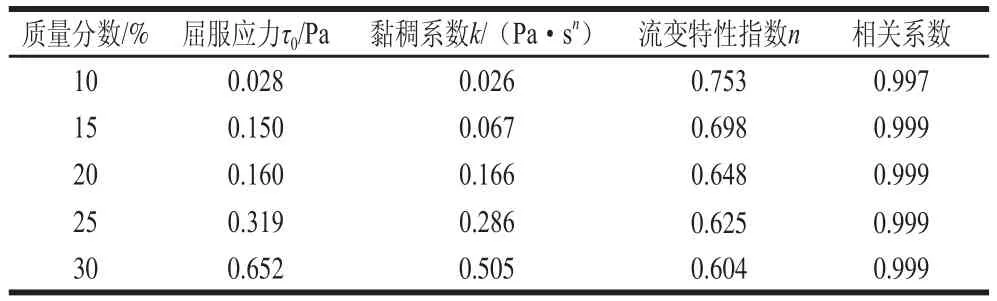
表1 不同质量分数芋头浆的流变特性参数值Table 1 Rheological parameters of taro pulp at different concentrations
由表1可知,在20 ℃条件下,随着质量分数的增加,芋头浆的流变特性指数逐渐减小,浆体的屈服应力和黏稠系数逐渐增大。流变特性指数的大小反映了浆体体系剪切变稀的难易程度,也即假塑性程度的大小,芋头浆的流变特性指数逐渐减小,意味着浆体的非牛顿性流体行为增强,牛顿性流体行为减弱。由于芋头浆中不仅存在大量的淀粉颗粒,同时还保留了蛋白质、果胶等大分子物质[16-17],这些大分子之间相互聚集形成网状结构,使得浆体体系具有屈服应力,而且随着质量分数的增加,各分子之间的相互作用增大,形成网络结构的致密程度增加,使得浆体体系所需克服的屈服应力就越大,黏稠系数也相应增大。曲线拟合的相关系数均在0.99以上,这说明在20 ℃条件下,质量分数10%~30%的芋头浆均服从Herschel-Bulkley模型。
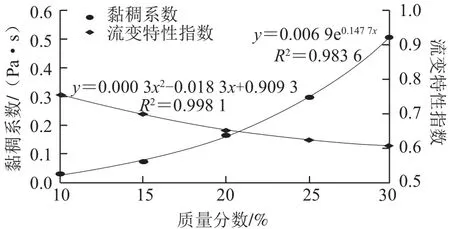
图3 20 ℃条件下芋头浆的黏稠系数和流变特性指数与质量分数的关系Fig.3 Effect of concentration on viscosity coeffcient and rheological indices of taro pulp at 20 ℃
由图3可知,20 ℃条件下芋头浆的黏稠系数k与质量分数呈指数函数关系,拟合的曲线方程为y=0.006 9e0.147 7x,相关系数R2=0.983 6;芋头浆的流变特性指数n与质量分数的数学关系符合二次多项式模型,拟合的曲线方程为y=0.000 3x2-0.018 3x+0.909 3,相关系数R2=0.998 1。
2.1.2 温度对芋头浆流变特性的影响
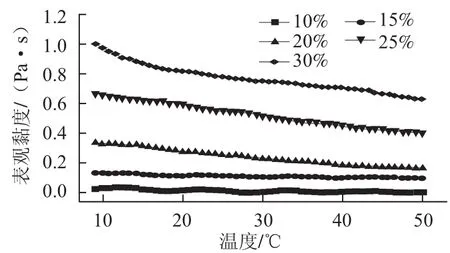
图4 不同质量分数芋头浆表观黏度随温度的变化曲线Fig.4 Relationship between temperature and apparent viscosity of taro pulp at different concentrations
由图4可知,不同质量分数芋头浆的表观黏度随着温度的升高在不断减小,且质量分数越大,这种减小的趋势更加明显。这主要是由于温度升高,浆体中淀粉等大分子物质的能量增加,加快了分子的热运动,减弱了分子间的相互作用,同时溶液体积发生膨胀,使得每一分子平均占有的体积增大,浆体的流动性增强,体系的黏度从而逐渐减小[18]。随着芋头浆质量分数的增加,相同体积内淀粉等大分子物质的含量增加,温度越高对体系黏度的影响就越大。

图5 质量分数15%的芋头浆在不同温度下剪切应力随剪切速率的变化曲线Fig.5 Relationship between shear rate and shear stress of 15% taro pulp at different temperatures
由图5可知,在不同温度下,质量分数15%芋头浆的剪切应力随着剪切速率的增加而增大;在同一剪切速率条件下,芋头浆的剪切应力随着温度升高逐渐减小。不同温度下15%芋头浆的流变曲线可采用Herschel-Bulkley模型进行拟合,得到的拟合参数见表2;对芋头浆的黏稠系数k和流变特性指数n与温度的数学关系进行拟合,所得曲线和方程见图6。
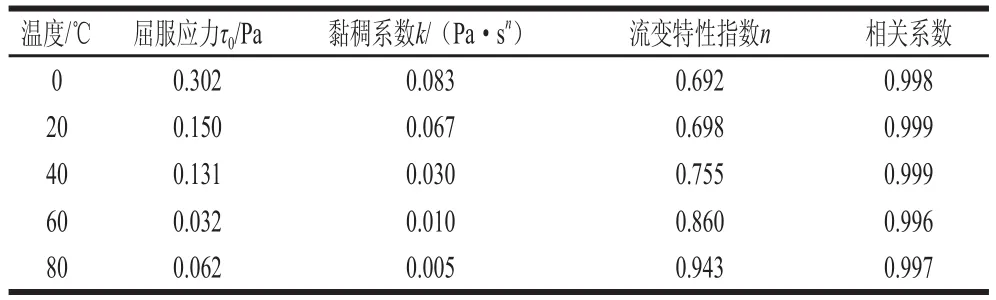
表2 质量分数15%的芋头浆在不同温度下的流变特性参数值Table 2 Rheological parameters of 15% taro pulp at different temperatures
由表2可知,随着温度的升高,质量分数15%芋头浆的流变特性指数逐渐增大,浆体的黏稠系数逐渐减小。芋头浆流变特性指数的增大意味着浆体非牛顿性流体行为的减弱,其中n值均小于1,说明在0~80 ℃之间,质量分数15%的芋头浆均属于假塑性流体体系。浆体的黏稠系数逐渐减小,这与之前表观黏度随温度升高逐渐减小的趋势表现一致。曲线拟合的相关系数值均在0.99以上,这说明在该温度范围内,15%芋头浆均服从Herschel-Bulkley流体模型。
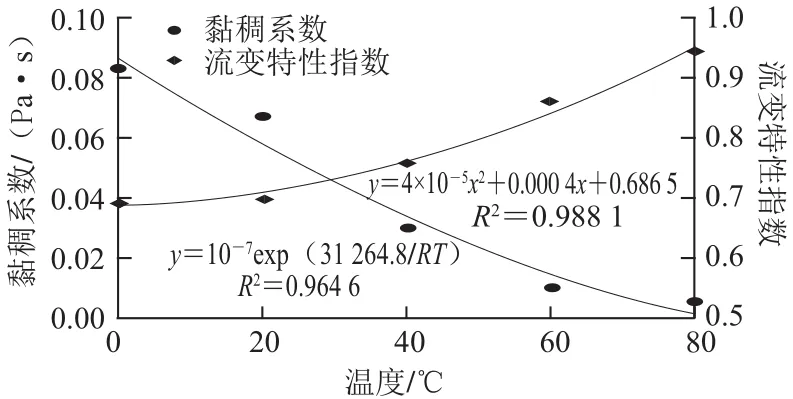
图6 温度对质量分数15%的芋头浆黏稠系数和流变特性指数的影响Fig.6 Effect of temperature on viscosity coefficient and rheological index of 15% taro pulp
采用Arrhenius方程k=k0exp(Ea/RT)对温度与芋头浆黏稠系数的数学关系进行拟合;式中:k0为系数,Ea为流动活化能/(J/mol),R为气体常数(8.314 J/(mol·K)),T为绝对温度/K。如图6所示,所得拟合方程k=10−7exp (31 264.8/RT),R2=0.964 6,温度与黏稠系数对Arrhenius方程具有很高的拟合精度,用Arrhenius方程可以很好地描述温度对芋头浆流动特性的影响。温度与芋头浆流变特性指数n的数学关系符号二次多项式模型,拟合的曲线方程为y=4×10−5x2+0.000 4x+0.686 5,相关系数R2=0.988 1。
2.2芋头浆动态流变性质
2.2.1线性黏弹区的确定
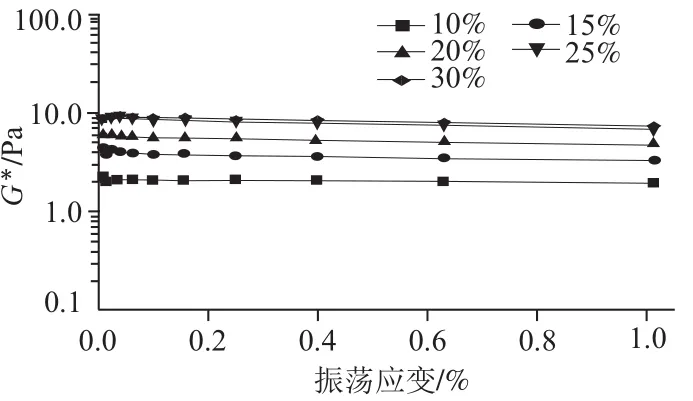
图7 不同质量分数芋头浆的线性黏弹性区域Fig.7 Linear viscoelasticity region of taro pulp at different concentrations
线性黏弹区是指复合模量G*不随振荡应变发生变化的区域[19],在线性黏弹区内,芋头浆的内部结构不会被破坏。由图7可知,不同质量分数芋头浆在振荡应变为0.0%~1.0%的范围内复合模量G*恒定,显示线性黏弹区。本实验选择0.5%的振荡应变作为测定芋头浆动态流变性质的条件。
2.2.2频率扫描
一般材料的动态黏弹性测定是通过对材料施加一个连续的正弦应力或应变,然后 记录材料的响应。G’是动态弹性模量,又称贮能模量,反映了材料贮存能量的能力,可以表征材料的弹性特征;G”是黏性损耗模量,又称耗能模量,反映了材料释放能量的能力,耗能模量G”和动力学黏度η’可以表征材料的黏性特征[19-20]。
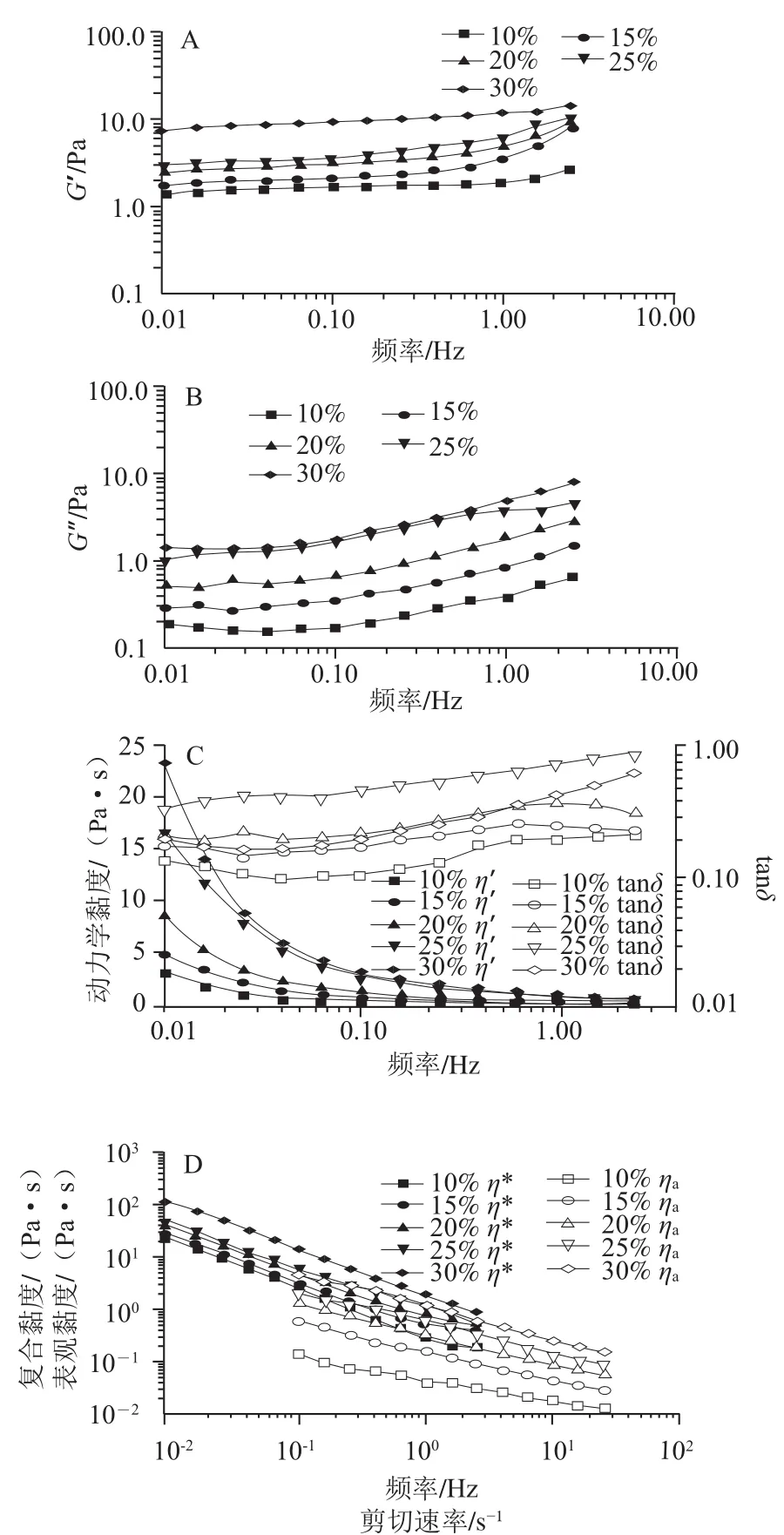
图8 不同质量分数芋头浆的频率扫描Fig.8 Frequency scanning of taro pulp at different concentrations
损失正切tanδ定义为耗能模量与贮能模量的比率,tanδ=G”/G’可以直观准确地反映流体的动弹黏弹性。当tanδ<1时,说明G’相对于G”占主要优势,流体主要表现为固体弹性性质,反之则主要表现为流体黏性性质[21]。由图8A、8B可知,在扫描的频率范围内(0.01~2 Hz),芋头浆的贮能模量G’始终高于耗能模量G”,其G’和G′对振荡频率具有轻微的依赖性,且两者的值均较小(0.1~20 Pa之间)。由图8C可知,损失正切tanδ基本保持在0.1~1之间,与扫描频率之间呈现弱相关性,芋头浆主要表现为固体弹性性质。由图8D可知,在振荡频率=剪切速率时,浆体的表观黏度明显低于复合黏度;这反映了芋头浆的弱凝胶特性[22]。事实上,真正的凝胶或完全弹性的固体,其G’比G”大得多,而且基本上不依赖于振荡频率[23]。大部分的食品体系或生物大分子溶液,通常都是介于完全液态和完全固态之间,属于黏弹性流体[24]。
在芋头浆体系中,G’代表的是蛋白质、果胶等物质表现的弹性行为,而G”则代表了糖类等小分子溶质表现的黏性行为,G’和G”随着芋头浆质量分数的增加而增大,是这些物质对浆体黏弹性绝对贡献程度增加的反映[12]。此外,类似于稳态实验的剪切稀化现象,在动态实验中,随着振荡频率的增加,芋头浆的动力学黏度η’呈现减小的趋势,这与静态流变学测定的结果一致。
3 结 论
芋头浆有剪切稀化的现象,是具有假塑性的非牛顿流体,其流变特性服从Herschel-Bulkley模型;随着芋头浆质量分数的增大,浆体体系的非牛顿性在逐渐增强,屈服应力和黏稠系数逐渐增大,流变特性指数逐渐减小;对于质量分数15%的芋头浆,随着温度的升高,浆体的非牛顿性逐渐减弱,黏稠系数逐渐减小,流变特性指数逐渐增大,温度与芋头浆黏稠系数的关系可用Arrhenius方程进行拟合;动态流变测定表明:芋头浆显示弱凝胶特性;此外,随着振荡频率的增加,芋头浆的动力学黏度η′逐渐减小,呈现剪切稀化的特性,这与静态流变学测定的结果一致。
参考文献:
[1]姜绍通, 程元珍, 郑志, 等. 红芽芋营养成分分析及评价[J]. 食品科学, 2012, 33(11): 269-272.
[2]姜绍通, 汪洪普, 潘丽军. 芋头多糖的分离纯化及对细胞免疫的调节作用[J]. 食品科学, 2013, 34(19): 287-292. doi: 10.7506/spkx1002-6630-201319059.
[3]程元珍. 红芽芋品质分析及其芋泥的加工研究[D]. 合肥: 合肥工业大学, 2012: 3.
[4]姜绍通, 程元珍, 汪洪普, 等. 红枣芋泥的配方优化及产品特性研究[J].中国食物与营养, 2013, 19(5): 43-47.
[5]李共国. 芋头喷雾干燥粉的加工工艺[J]. 现代商贸工业, 2004(1): 45-46.
[6]陈运中, 刘章武. 甘薯(芋头)冰淇淋工艺和配方研究[J]. 武汉轻工大学学报, 1994(2): 7-10.
[7]陈运中. 芋头系列食品加工技术[J]. 食品工业科技, 1994, 15(5): 63-66.
[8]李纯, 周文倩, 胡瑞, 等. 葛根全粉浆的流变特性[J]. 食品科学, 2013, 34(23): 165-169. doi: 10.7506/spkx1002-6630-201323035.
[9]段翰英, 李爱军, 李远志. 香蕉浆料流变学性质的研究[J]. 食品科学, 2004, 25(4): 62-64.
[10]罗昌荣, 麻建国, 许时婴. 番茄浆料的流变特性研究[J]. 食品科学, 2001, 22(7): 28-32.
[11]CEPEDA E, HERMOSA M, LLORENS F, et al. Rheological behaviour of blueberry cloudy juice (Vaccinium corymbosum L.)[J]. International Journal of Food Science and Technology, 2002, 37(3): 271-276.
[12]许学勤, 朱巧力, 徐莹秋. 芒果浓缩汁的流变学特性[J]. 食品与生物技术学报, 2011, 30(1): 32-36.
[13]包海蓉, 陈必文, 邬瀛洲. 浓缩葡萄汁流变特性研究[J]. 食品科学, 2004, 25(10): 70-72.
[14]杨彬, 周裔彬, 陈俊芳, 等. 莲子淀粉的流变性初步研究[J]. 食品研究与开发, 2011, 32(11): 40-43.
[15]胡珊珊, 王颉, 孙剑锋, 等. 羟丙基木薯淀粉流变特性的研究[J]. 食品科学, 2012, 33(17): 73-77.
[16]LU Tingjiang, LIN Henghua, CHEN Jiaci. Characteristics of taro (Colocasia esculenta) starches planted in different seasons and their relations to the molecular structure of starch[J]. Journal of Agricultural and Food Chemistry, 2008, 56(6): 2208-2215.
[17]孙忠伟. 芋头淀粉的提取及其性质的研究[D]. 无锡: 江南大学, 2004: 5.
[18]吴其晔, 巫静安. 高分子材料流变学[M]. 北京: 高等教育出版社, 2005: 45-46.
[19]杨述, 高昕, 于甜, 等. 4种蛋黄酱的流变特性比较研究[J]. 食品科学, 2011, 32(15): 121-125.
[20]杨仁党, 陈克复. 甘蔗渣碱法制浆废液多聚物的动态粘弹特性[J].华南理工大学学报: 自然科学版, 2003, 31(4): 93-96.
[21]汪海波, 王孟津, 张寒俊, 等. 草鱼鱼鳞胶原蛋白的流变学性能研究[J].食品科学, 2009, 30(23): 138-142.
[22]IKEDA S, NISHINARI K. “Weak gel”-type rheological properties of aqueous dispersions of nonaggregated κ-carrageenan helices[J]. Journal of Agricultural and Food Chemistry, 2001, 49(9): 4436-4441.
[23]RAO M A, COOLEY H J. Rheological behavior of tomato pastes in steady and dynamic shear[J]. Journal of Texture Studies, 1992, 23(4): 415-425.
[24]罗昌荣, 麻建国, 许时婴. 破碎温度对番茄浆流变性质与果胶分子结构的影响[J]. 食品科学, 2001, 22(8): 24-29.
Rheological Properties of Taro Pulp
YU Zhenyu, JIANG Shaotong*, PAN Lijun, DAI Yuanyuan, LÜ Xiaying
(Key Laboratory for Agricultural Products Processing of Anhui Province, Institute of Agricultural Products Processing Technology, School of Biotechnology and Food Engineering, Hefei University of Technology, Hefei 230009, China)
Abstract:Our present work evaluated the rheological properties of taro pulp at different concentrations and temperatures. Static rheological tests showed that taro pulp was a pseudoplastic non-Newtonian fl uid and could be fi tted by Herschel-Bulkley model within the corresponding ranges of temperature (0‒80 ℃) and concentration (10%–30%). An in crease in taro pulp concentration enhanced its non-Newtonian characteristics, increased its viscosity coeffi cient and shear stress and decreased its rheological index, while higher temperature could result in higher rheological index, lower non-Newtonian fl uidity and smaller viscosity coefficient. The Arrhenius equation could accurately describe the relationship between temperature and viscosity coeffi cient of taro pulp. Dynamic rheological tests showed that taro pulp had weak gel-li ke properties.
Key words:taro pulp; rheological properties; Herschel-Bulkley model; gel-like properties
doi:10.7506/spkx1002-6630-201507007
中图分类号:TS201.7
文献标志码:A
文章编号:1002-6630(2015)07-0036-05
*通信作者:姜绍通(1954—),男,教授,本科,研究方向为农产品加工。E-mail:jiangshaotong@163.com
作者简介:余振宇(1992—),男,硕士研究生,研究方向为农产品加工。E-mail:elvenyue@163.com
基金项目:安徽省科技专项资金项目(13Z03042)
收稿日期:2014-06-30
