基于非平整地面的轮腿复合机器人运动学研究
2015-03-17冯晓阳郭海青
冯晓阳,郭海青
(第一拖拉机股份有限公司 工艺材料研究所,河南 洛阳 471004)
基于非平整地面的轮腿复合机器人运动学研究
冯晓阳,郭海青
(第一拖拉机股份有限公司 工艺材料研究所,河南 洛阳 471004)
针对一种轮腿复合机器人进行了运动学分析,得到机器人在平整地面上的运动学模型。在此基础上将非平整地面对机器人运动的影响简化为两个力作用在机器人上,建立机器人在非平整地面上的运动学方程。利用Matlab软件仿真分析了几种典型路况下机器人的运动情况。仿真结果表明,当机器人在地面波动类似方波和三角波的地面上行走时,机器人参考点的位姿与静止目标位姿之间的偏差最大。从而为机器人的控制系统的设计提供了一个详细准确的运动学方程。
轮腿移动机器人;运动学分析;非平整地面
0 引 言
随着我国石化产业的快速发展及原有设备的不断老化,事故发生的概率在不断提高,为减少石化事故发生,因此,迫切需要能够适应油气田和石化企业等大空间作业环境下进行紧急救援任务的危险作业机器人[1]。本文设计了一种新型的轮腿复合移动机器人,通过前后轮腿的摆动和车体中部的调节使得机器人能够适应各种复杂的地形。
主要研究并建立机器人在非平整地面上运动时的运动学模型,在此基础上, 考虑对机器人运动产生最大影响的车体横摆运动和侧向平移运动特性,建立将横摆角度、侧向位移、地面扰动激励等作为状态变量的轮腿复合机器人运动学模型。通过仿真实验验证模型的正确性、有效性[2-5]。
1 轮腿复合机器人结构和行进策略
1.1 总体结构
机器人结构见图1。车体有前轮腿系统、车身和后轮腿系统3部分组成。车身与前后轮腿系统之间采用铰链连接,通过车身上安装的调倾电机,可随时调整车身的位置进而改变机器人整体重心的位置,以便能更好地适应各种地形。
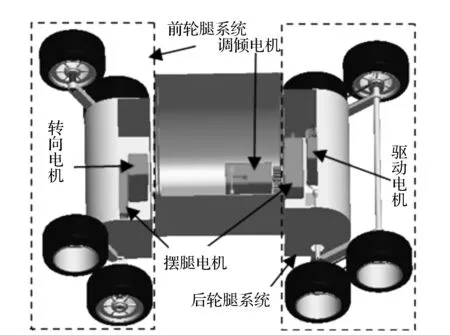
图1 轮腿复合机器人Fig.1 Wheel-legged mobile robot
轮腿机器人除具有普通移动机器人的行走功能外,还可通过前后轮腿系统的摆动实现机器人的变形,从而改变机器人重心的位置,增加机器人系统的自由度数,能适应各种复杂地形。
1.2 行进策略
轮腿复合机器人根据作业环境的不同有3种行进策略,即正常行进策略、越障策略和转向策略。在进行运动学分析时,为了简便将各种地形简化为类似台阶和凹槽两种。车轮半径R=100 mm,台阶高度H,沟槽宽度s、深度h,轮腿系统两轮的中心距S1=230 mm、两轮外侧距离S2=430 mm。
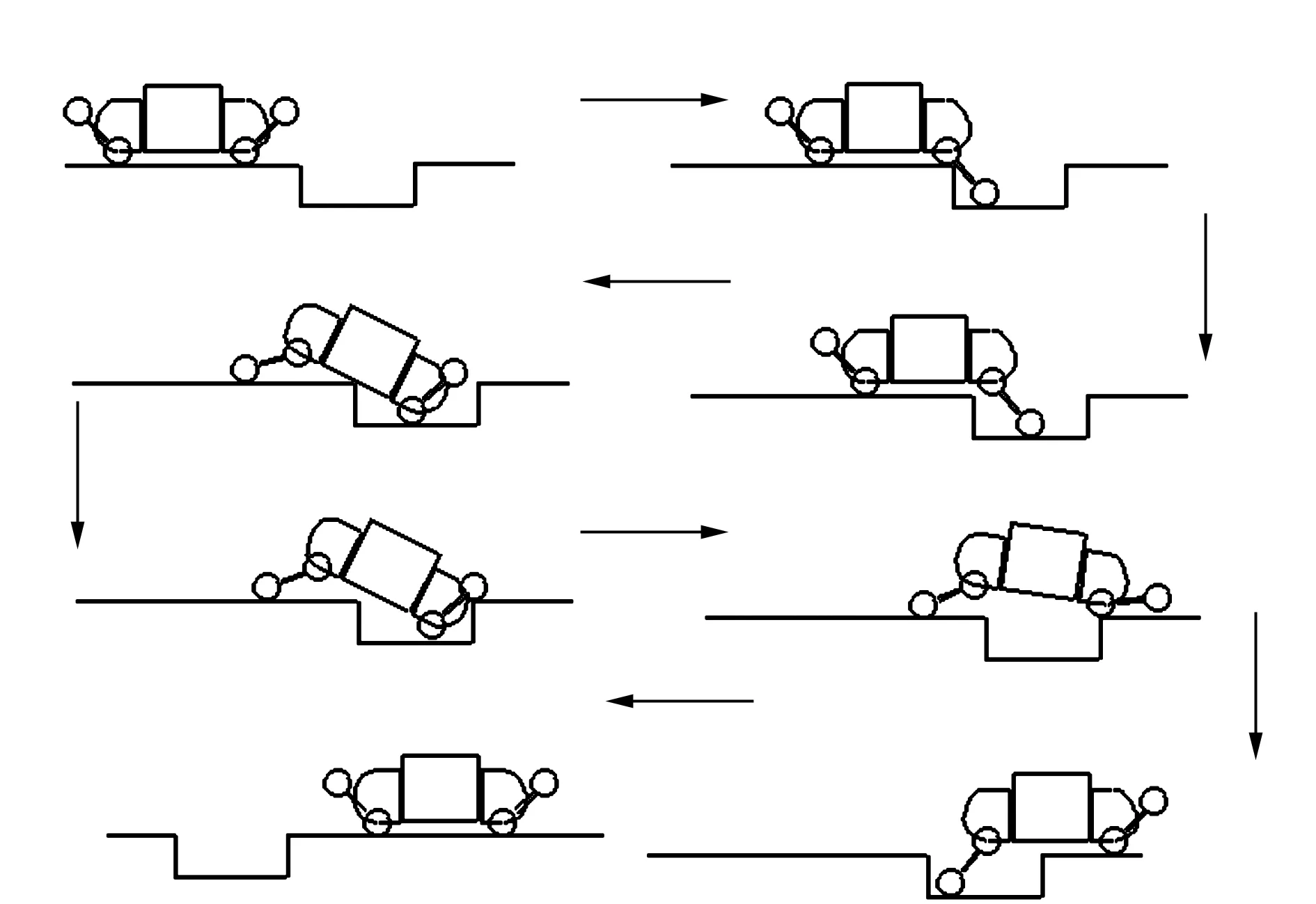
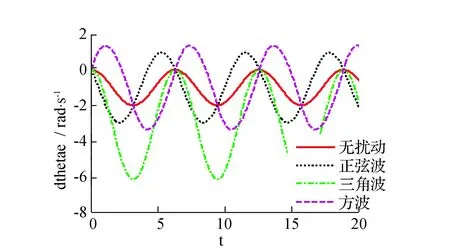
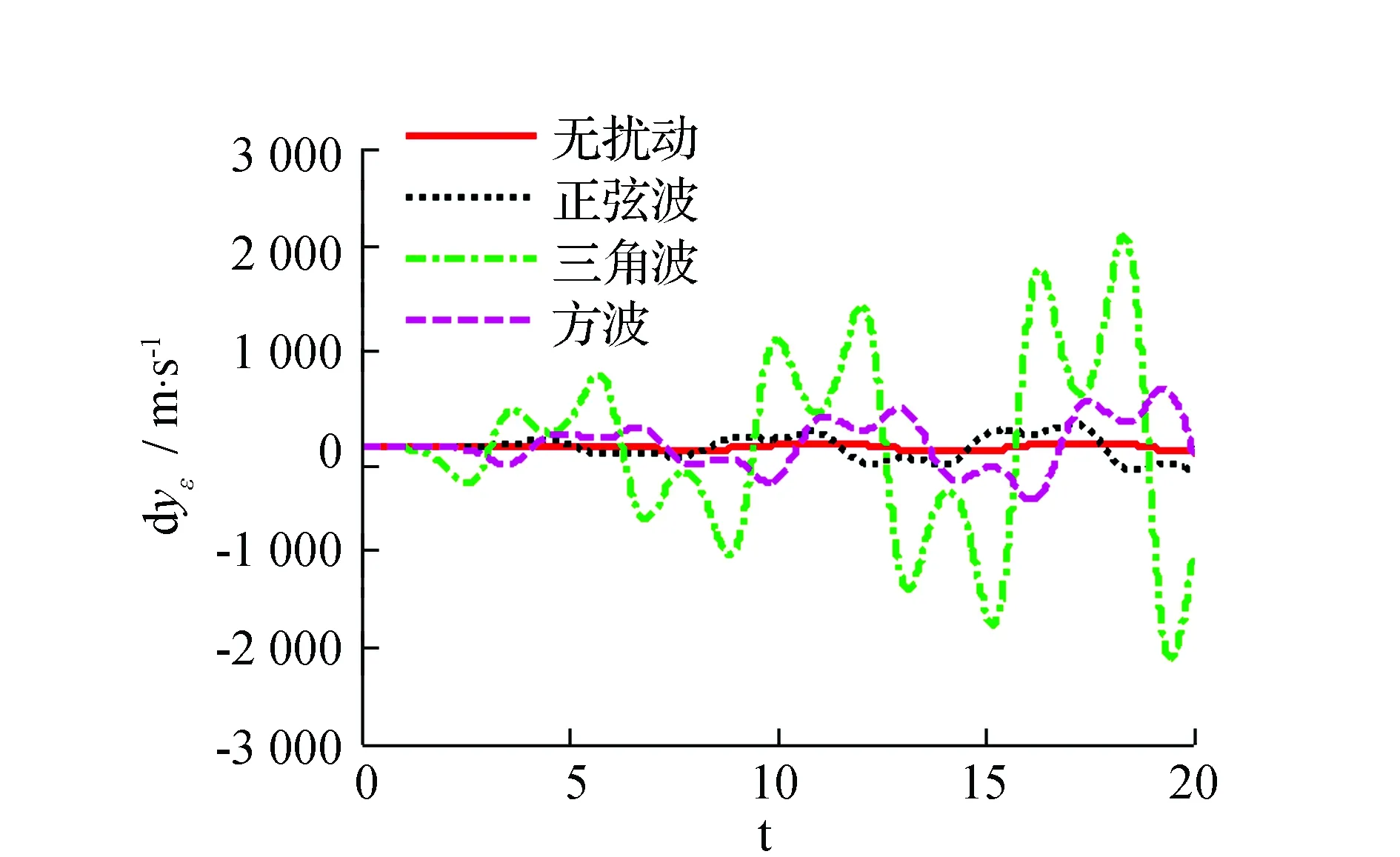
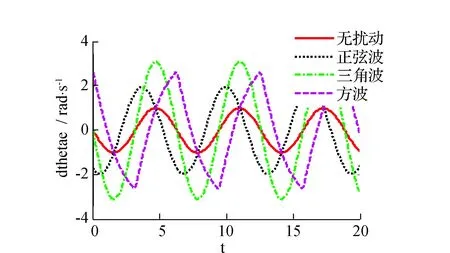
1.2.1H、h 机器人不需作姿态调整,可直接跨越。 1.2.2H>R 机器人的行进策略见图2。 图2 轮腿复合机器人跨越台阶姿态调整示意图Fig.2 Robot across a step posture schemes 1.2.3s≤S1 机器人行进策略见图3。 图3 轮腿复合机器人跨越较窄沟槽姿态示意图Fig.3 Robot across a narrow groove posture schemes 1.2.4s>S1 在遇到此类地形时,机器人需要通过摆动前后轮腿系统来完成一个类似上下台阶的动作过程来跨越此类的障碍物。因此沟槽的深度应满足h≤250 mm。机器人的行进策略见图4。 图4 机器人跨越较宽沟槽姿态示意图 Fig.4 Robot across a wide groove posture schemes 当遇到高于250 mm的障碍时,轮腿复合机器人不能跨越障碍,则只能采取转向策略。 2 轮腿复合机器人运动学模型建立2.1 平整地面下的机器人运动学模型 运动学方程的建立基于以下前提条件: 1)不考虑车轮与地面的弹性变形。 2)假设机器人的运动速度不高。 3)机器人移动时为纯滚动无侧滑。 4)不考虑机器人的垂直及俯仰运动的影响。 建立地面坐标系x-o-y(图5),机器人运动时的相对坐标系X-O2-Y。机器人运动时相对坐标系x-o-y的转角为θ,机器人速度的瞬心、质心分别用O1、O2(通过机器人本体几何尺寸确定)表示。前后轮轴到质心的距离l1、l2,运行时机器人前后轮相对于坐标系X-O2-Y的转角为α、β(假设左右前轮、后轮的转角分别相等)。A点为两前轮轴线的中点,B点为后两轮轴线的中点且设为参考点。VA为前轮轴中心的速度矢量,VB为后轮轴中心的速度矢量,V为机器人质心处的速度矢量。 图5 机器人运动学模型简图Fig.5 Robot kinematics model diagram 为求得机器人质心O2在x-o-y的位置,以机器人后轮轴轴心B为参考点,得方程(1): (1) 以机器人质心O2为基准点,将机器人后两轮轴轴心速度VB在地面坐标系x-o-y进行分解,得机器人的运动学模型为: (2) 后轮侧偏角β一般较小,将其忽略,则式(2)可变为: (3) 由式(3)推导出机器人的微分约束方程为: (4) 对式(3)第三分式的两边求导: (5) 根据式(3)~式(5)并将机器人后轮驱动轮的速度VB=V带入,可得以O2点为基准的移动机器人的运动学模型为: (6) X、Y、θ为表示机器人姿态的状态变量,v、ω称为机器人的控制变量。 2.2 机器人运动学误差模型 由于机器人的期望位姿与实际位姿通常不一致,在机器人运动过程中要时刻对机器人的姿态进行监控并修正,将机器人的目标位置与实际位置作比较,得机器人的偏差并将其作为输入代入机器人的运动学方程中,减小机器人的运动误差。 大地坐标系X-O-Y,固连在机器人上的相对坐标系X0-O0-Y0,机器人的实际位置用机器人质心O0表示,θ为机器人本体相对大地坐标系X-O-Y的转角(图6)。机器人运动时的平移速度、角速度分别为v0、ω0,点O1为机器人的目标位置,θ1为相对绝对坐标系的转角,目标机器人的平移速度、角速度分别用v1、ω1表示。 图6 机器人运动示意图Fig.6 Robot motion diagram (7) (8) (9) 推导出: (10) 其中R为坐标旋转变化的矩阵。 对式(10)两边求导,可得: (11) 综合以上公式分析并考虑微分约束方程,推导出机器人误差微分方程为: (12) 2.3 考虑地面扰动力的机器人运动学模型 本文拟建立在非平整地面的轮腿复合机器人运动学模型。机器人在非平整地面上行驶时,可将地面路况变化对机器人运动的影响等价为一个随地面情况变化的力与力矩的直接作用,该力在机器人运动平面可分解为力FH,在与机器人运动平面垂直平面上分解为力FV,由于FV垂直于机器人的运动方向,对机器人的平面运动不做功,因此可以忽略不予考虑,将力FH在机器人运动平面内分解为沿机器人行进方向的力F1和与机器人运动方向其垂直的力F2。力F1直接影响机器人的运行速度,力F2影响机器人的运动方向。因此机器人在非平整地面上的运动状态可由作用力F1、F2表示[6]。 初始时刻t0的机器人平移速度、角速度分别为v、ω,设在Δt时间内,机器人的速度、角速度变化为Δv、Δω,则在t0+Δt时刻机器人的平移速度为v+Δv,角速度为ω+Δω。根据式(12)推导出机器人在t0+Δt时刻的运动学方程为: (13) 机器人的质量为m,转动惯量为J,根据动量定理可推导出[7]: (14) 推导出机器人的速度变化: 根据动量矩定理: (15) 其中d为机器人的旋转半径。 机器人的角速度变化: 将以上式子整理可得: (16) 假设目标机器人的位置是静止的,则有v1=0、ω1=0,推导出在非平整地面上机器人运动控制的整定模型: (17) 实际路况的种类较多。利用Matlab仿真在不同地面激励的情况下机器人的运动情形时,选用几类典型的有相同周期与幅值的正弦波、三角波、方波周期激励代表几种典型的非平整地面。为了能清晰反映机器人在这几种典型波动下的运动趋势,验证机器人的运动控制模型,选用几种激励的幅值较大,仿真结果并不能代表机器人在真实路况上的运动情况,仿真结果见图7~图12。 图7 xε在3种周期扰动力作用下的对比响应图Fig.7 xεcontrast response chart under the action of three kinds of periodic disturbing forces 图8 yε在3种周期扰动力作用下的对比响应图Fig.8 yεcontrast response chart under the action of three kinds of periodic disturbing forces 图9 θε在3种周期扰动力作用下的对比响应图Fig.9 θεcontrast response chart under the action of three kinds of periodic disturbing forces 图在3种周期扰动力作用下的对比响应图Fig.10 contrast response chart under the action of three kinds of periodic disturbing forces 图在3种周期扰动力作用下的对比响应图Fig.11 contrast response chart under the action of three kinds of periodic disturbing forces 图在3种周期扰动力作用下的对比响应图Fig.12 contrast response chart under the action of three kinds of periodic disturbing forces 由图7~图12可见,在没有扰动的情况下,机器人的各个状态变量都在一定的范围内变化。说明在没有扰动时机器人的运动比较平稳。 在考虑地面扰动的情况下,机器人的各个参数变化相对于无扰动时变化比较剧烈,且变化趋势没有规律,尤其是在有三角波扰动时机器人的各参数变化随着时间的推移越来越大,说明机器人与目标点的偏差也越来越大,对机器人运动路径的控制提出了很高的要求,因此在设计机器人运动控制时要充分考虑各种地面扰动对机器人运动的影响[8-9]。 本文基于平整地面的机器人运动学方程,将非 平整地面对机器人运动的影响等价为一个随地面情况变化的力和力矩,建立了考虑非平整地面下的轮腿机器人运动学方程。本研究成果可为机器人的稳定性控制研究奠定基础,同时其建模与分析方法也可借鉴到其它类型机器人非平整地面下的运动学、动力学研究。 [1]刘 静,赵晓光,谭 民.腿式机器人的研究综述[J].机器人,2006,28(1):487-492. [2]刘娟秀,吴益飞,郭 建.一种平地楼梯两用助行机器人的建模与仿真分析[J].工程设计学报,2015,22(4):344-350. [3]吕应柱,郭瑞峰,黄金荣.新型码垛机器人的结构设计与运动学分析[J].组合机床与自动化加工技术,2015,(6):40-42. [4]孙详溪,罗庆生,苏晓东.工业码垛机器人运动学仿真[J].计算机仿真,2013,30(3):303-306. [5]范宇超,牛永利.基于DMAC的3自由度并联机器人的控制研究[J].黑龙江大学工程学报,2015,6(2):92-95. [6]江水明. 六轮自主移动机器人动力学建模与控制研究[D]. 南京:南京理工大学,2005. [7]宋孟军,张明路.多运动模式移动机器人的可变形轮腿运动学分析[J].机械设计,2011,28(5):47-50. [8]冯虎田 ,欧 屹,高晓燕.小型地面移动机器人特殊运行姿态动力学建模与分析[J]. 南京理工大学学报,2006,30(4):822-855. [9]王洪斌,李 程,王跃灵,等.基于Arduino和蓝牙技术的六足机器人控制系统设计[J].黑龙江大学自然科学学报,2015,32(4):533-537. Kinematic analysis of wheel-legged mobile robotbased on the uneven terrain FENG Xiao-Yang,GUO Hai-Qing (YTO Group Corporation, Technology and Material Institute, Luoyang 471004,Henan,China) The kinematics analysis of the wheel-legged mobile robot platform is presented. Then the robot’s kinematics equation is built when the robot moves on the normal terrain. The influence on the robot of the uneven terrain environment is transformed into two forces, building the kinematics equation when the robot moves under the influence of uneven terrain, and used Matlab to verify the kinematics equation through simulating several typical terrains. The result shows that the position deviation between the reference point of robot and the stationary target is the biggest when the robot moves on the uneven terrain such as square wave and triangle wave. Thus a detailed kinematics equation for the control system of the robot is provided. wheel-legged mobile robot; kinematics analysis; uneven terrain 10.13524/j.2095-008x.2015.04.070 2015-09-10; 2015-11-06 天津市科技计划项目(10ZCKFSF01400) 冯晓阳(1987-),男,河南郑州人,工程师,研究方向:机器人设计与应用,E-mail:fxy19870601@126.com。 TP242 A 2095-008X(2015)04-0083-06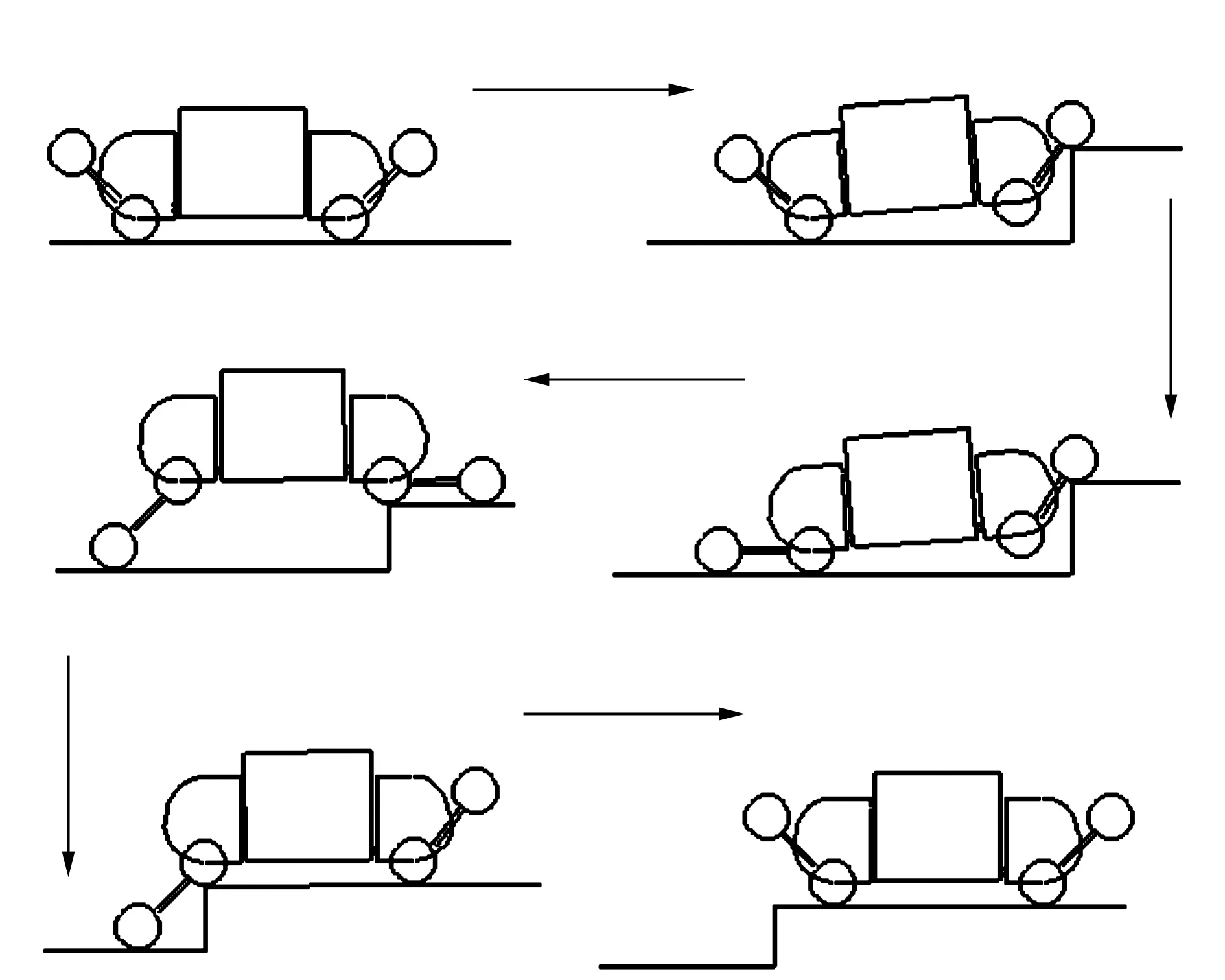


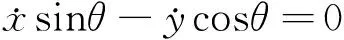
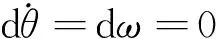


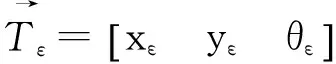
3 仿真与结果分析



4 结 论
