改进的BP神经网络在松花江干流水位预报中的应用

刘文斌，赵思远，郝振纯，*，王茂枚，马喜荣，尼玛旦增

(1.黑龙江省水文局，哈尔滨 150001；2.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098；3.江苏省水利科学研究院，南京 210017；4.珠江水利科学研究院，广州 510611；5.西藏自治区水文水资源勘测局 山南分局，西藏 山南 856000)

改进的BP神经网络在松花江干流水位预报中的应用

刘文斌1，赵思远2，郝振纯2，*，王茂枚3，马喜荣4，尼玛旦增5

(1.黑龙江省水文局，哈尔滨 150001；2.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098；3.江苏省水利科学研究院，南京 210017；4.珠江水利科学研究院，广州 510611；5.西藏自治区水文水资源勘测局 山南分局，西藏 山南 856000)

松花江干流水位受上游来水和水库调蓄等多因素的共同作用而表现出非线性响应，采用典型的3层BP神经网络模型来模拟松花江干流肇源、哈尔滨、通河、佳木斯和富锦5个代表站点水位。鉴于BP神经网络学习收敛速度慢、参数选择困难、易陷入局部极小值等缺点，分别采用Levenberg-Marquart算法和基于遗传算法的BP算法来建立水位预报模型，并对预报结果进行了分析和比较。结果表明：两种算法收敛速度快，预报精度均能达到预报要求。特别是将遗传算法的全局搜索和BP网络局部精确搜索的特性有机结合，做到了优势互补，在河流水位预报方面有着广阔的应用前景。

BP神经网络；Levenberg-Marquart算法；遗传算法；水位预报

0 引 言

松花江有南、北两源，南源为第二松花江，北源为嫩江，两江在三岔河汇合后，折向东流，经肇源、哈尔滨、宾县、木兰、通河、依兰、佳木斯、富锦等市县，于同江市同江镇汇入黑龙江，这段河道称为松花江干流。干流右岸有拉林河、蚂蚁河、牡丹江、倭肯河等注人；左岸有呼兰河、汤旺河、梧桐河等注入。干流长939 km，流域面积为18.64×104km2，占全流域面积(55.68×104km2)的33.5%。

松干流域地处北温带季风气候区，大陆性气候特点非常明显，春季干燥多风，夏季炎热多雨，秋季很短，冬季寒冷漫长，年内温差很大。流域内多年平均降水量约500 mm，降水年内分配不均，多处于季风控制的夏季7—8月，6—9月汛期降水量可占全年的70%～80%，降水在多年之间有明显的丰枯交替特点[1]。松干流域以平原为主，是我国重要的农业、工业、能源基地，也是我国最主要的商品粮基地之一。由于降水的时空分布不均，该流域成为了洪涝灾害频发地区，因此，建立各站点水位预报工作对松花江干流及沿岸的防洪调蓄有着重要的意义。

1 研究方法

人工神经网络是由大量简单的神经元相互连接而成的自适应非线性动态系统。它具有分布存贮和并行处理等特点及自组织、自学习的能力，利用其极强的非线性函数逼近能力，能对难以精确描述的复杂非线性对象进行建模，从而实现对复杂非线性对象进行有效的模拟[2-3]。因此，神经网络在洪水预报上得到了广泛的应用，只要给出历史水文观测资料，神经网络就可通过自身的学习来完成洪水的预报工作。

本文采用神经网络方法进行水位预报。BP神经网络通常为输入层、隐含层、输出层的3层网络模型，并通过权重、偏差、激活函数等来增强网络解决复杂问题的能力。其学习过程可分为信号正向传播和误差信号反向传播两个阶段。BP训练算法默认采用梯度下降法，但存在线性收敛速度慢、容易陷入局部极小值等缺陷。针对标准BP算法存在的一些不足，本文采用两种基于标准BP算法的改进算法。

1.1 LM算法

LM(Levenberg Marquart)算法实际上是梯度下降法和拟牛顿法的结合。通常，梯度下降法在开始几步下降较快，但随着接近最佳值，由于梯度趋于零，使得目标函数下降较慢；而拟牛顿法可以在最佳值附近产生一个理想的搜索方向[4]。通过自适应调整阻尼因子来进行收敛，提高了收敛速度，因而训练速度比其他算法快。LM算法公式如下：

(1)

式中wb为联接权值和阈值的向量；j(k)为一阶雅可比矩阵；I为单位矩阵；mu为阻尼因子。

1.2 GA-BP算法

采用遗传算法优化网络初始权重，实际上是将整个网络训练分成了2部分：①采用遗传算法优化网络的初始权重；②利用BP算法最终完成网络训练。这样能同时搜索函数曲线中多个个体，全局搜索能力极强，不容易陷入局部极小值的特点，是一种优秀的全局寻优的非线性优化方法。

GA-BP算法的建模过程简介如下：(1)首先确定采用典型的3层网络结构，输入层和输出层神经元节点数由不同站点已知，根据经验公式先确定隐含层节点数范围，再通过遗传算法优化网络初始权重，主要内容有：染色体的表达、目标函数和适应度函数的定义、进化算子和遗传算子的构造等[5-7]。(2)以步骤(1)得到的优化权重为输入参数，代入BP模型试算，经过输入样本的训练最终得出稳定的神经网络权值。

2 应用实例

2.1 神经网络模型的建立

松花江干流的水文水位观测站共有9个，即肇源、三家子、涝州、哈尔滨、木兰、通河、依兰、佳木斯、富锦，松花江干流水系概化图见图1。在松花江干流范围内，根据《水文情报预报规范》[8]对资料的要求，按照易获取、资料连续、代表性强等原则，选取肇源、哈尔滨、通河、佳木斯、富锦5个代表站点，均采用2008—2012年汛期水位逐日观测资料作为训练样本，选择2013年汛期水位逐日观测资料作为测试样本，建立各站点神经网络水位预报模型。

图1 松花江干流水系概化图Fig.1 Water generalization map for mainstream of Songhuajiang River

通常上游洪水过程与下游洪水过程具有很好的相关性，同时，利用下游的时间序列建模也能获得较好的预报结果，因此在做下游洪水水位预报时，上游与下游过去时刻的水位过程都是重要的影响因子。此外，由于松花江干流流域内水库与细小支流繁多，因此需要从备选输入变量中挑选出对因变量影响较大的一些因子建立模型[9]。本文使用逐步回归筛选法来挑选上边界入流站点。逐步回归筛选法是一种双重检验的方法。对于未选入方程的因子，只要它还可以提供显著的解释信息，能使残差平方和下降最多，就可以进入方程；而对于已进入方程的因子，只要在已建立的过渡方程中不显著，就要从方程中剔除。通过逐步回归模型引入方程的因子，一定是对预报对象影响显著的因子，此外，它还可以避免因子对预报对象的重复影响。

松花江干流流域站点水位观测数据是基于假定基面所测得的高程值，而从2012年汛期开始，假定基面改变导致水位观测值发生变化，从而影响到水位预报模型建模过程和预报结果。为了尽可能准确地预报各站点水位，同时消除水位的非平稳性影响，对水位时间序列作一阶差分变换，即水位涨差，例如Δh=ht-ht-1，单位为m。整个神经网络水位预报模型计算步骤为：将该站点自身t-1日8时水位涨差及上边界入流t日8时以前水位涨差归一化后作为神经网络的输入层节点，采用“试算法”来训练模型的主要参数，包括隐含层神经元节点数，学习速率及目标精度等，以获取最佳的模拟效果，从而计算输出反归一化后得该站点t日8时水位涨差预报值，再加上该站点t-1日8时水位，可得该站点t日8时预报水位值。各站点模型运行基础数据具体描述见表1。

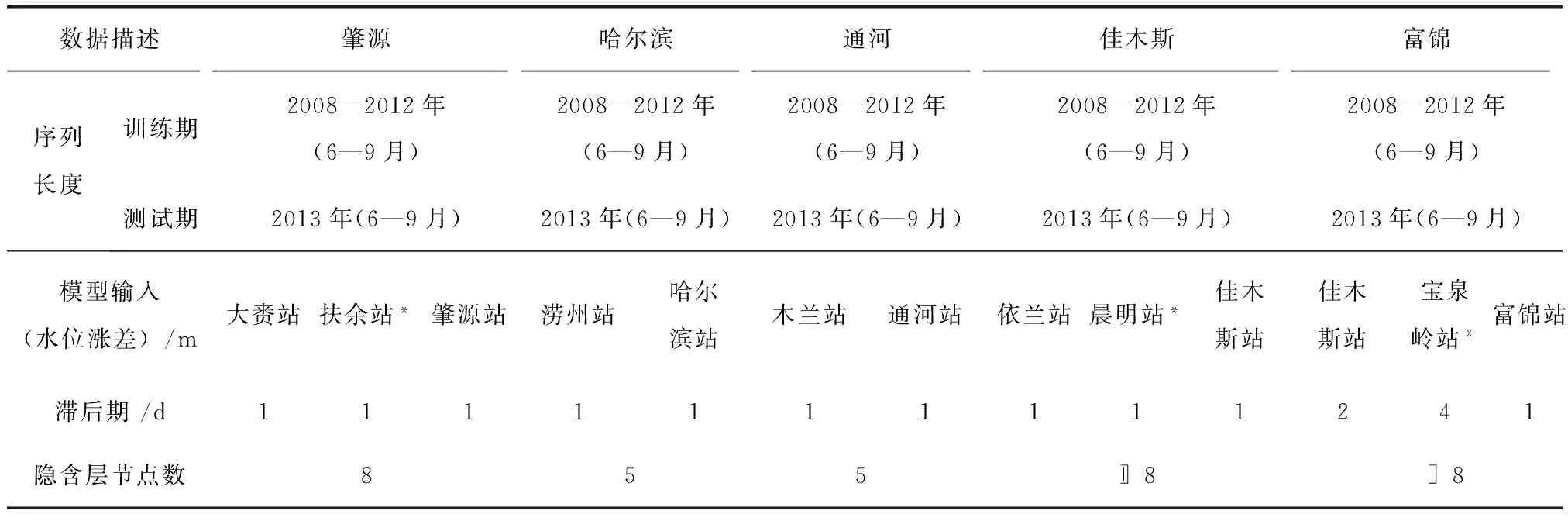
表1 基础数据

注：*为支流站作为模型输入。

对于上述2种基于改进的BP神经网络的水位预报模型，考虑到模型结果对学习速率和迭代次数的敏感性较低，在训练过程中设置学习速率为0.001，最大迭代次数为5 000次。目标精度随预报站点不同而改变，隐含层节点数目通过试算确定，其余训练参数取默认值。遗传算法在运行过程中的重要参数设置为：种群规模为100，迭代次数为100，选择概率为0.1，交叉概率为0.2，变异概率为0.1。

2.2 评估准则

根据文献[8]，可以采用许可误差和确定性系数作为方案精度评定标准，本文主要采用变幅均方差来量化许可误差，采用均方根误差(RMSE)和确定性系数(DC)量化模型的模拟结果。RMSE表示模型总体预报的精度水平，DC表示洪水预报过程与实测过程之间的拟合程序。模型评估以DC接近于1、RMSE趋于0 m为最佳拟合效果。具体计算方法如下：

(2)

(3)

(4)

2.3 预测结果及分析

上述2种水位预报模型均选取2008—2012年的汛期(6—9月)水位作为训练样本，以2013年汛期(6—9月)水位作预测样本，每个站点2种算法的有效预见期为24 h。要选择出符合实际情况的神经网络模型，其中最关键的一步是利用预测样本来不断测试已经训练好的模型，直到选出适合的模型。而判断一个BP神经网络是否符合实际情况，主要观察其预测能力的高低，为此必须利用测试数据对已训练好的模型进行检验。

2种基于改进的BP神经网络的松花江干流5个站点的水位预报模型模拟效果见表2。由表2可见，由于在模型计算过程考虑用水位涨差代替水位变化，除了佳木斯站以外其它站点2种算法的预报合格率均达到90%以上，确定性系数也都为0.99以上，因此各站点的2种算法的预报方案均评定为甲级方案。由表2可知，在相同网络结构、传递函数及期望误差等条件下，两种算法模型均具有收敛速度快、预测精度高、不易陷入局部极小值等优点。其中LM算法是为了训练中等规模的前馈神经网络而提出的最快速算法，因此它的学习收敛速度要比GA-BP算法快很多。各站2种算法的拟合效果见图2～图6。

表2 各站BP神经网络模型2013年水位预报精度统计

图2 肇源站2013年汛期(6—9月)水位过程预报检验Fig.2 Verifying the validity of water-level forecasting for flood season in 2013(June to September) for Zhaoyuan Station

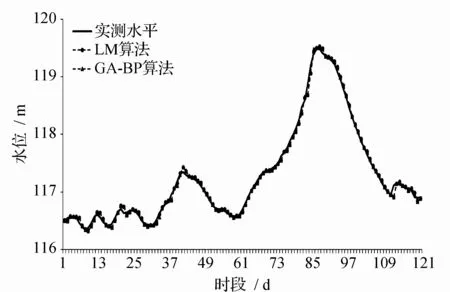
图3 哈尔滨站2013年汛期(6—9月)水位过程预报检验Fig.3 Verifying the validity of water-level forecasting for flood season in 2013(June to September) for Harbin Station

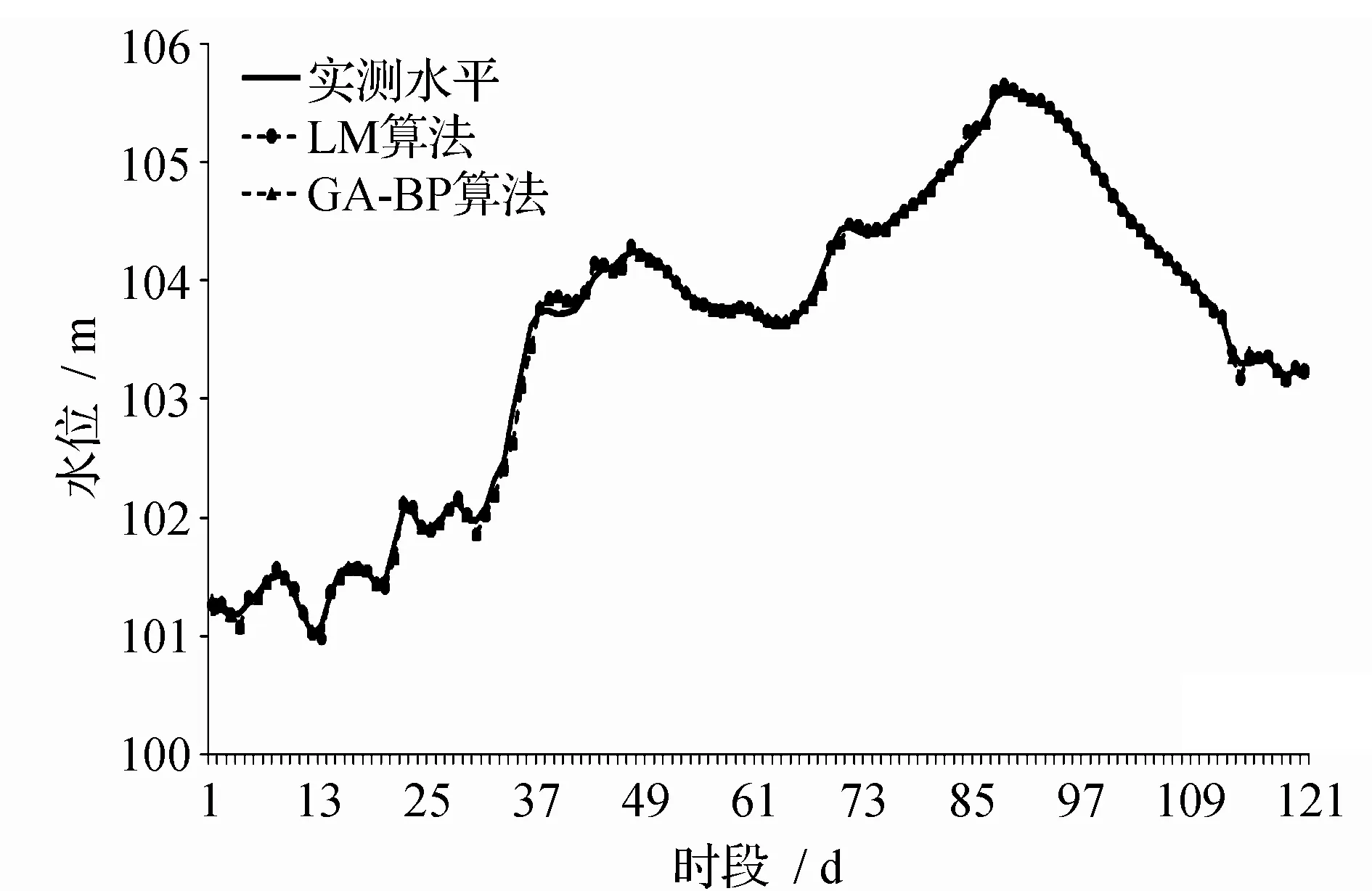
图4 通河站2013年汛期(6—9月)水位过程预报检验Fig.4 Verifying the validity of water-level forecasting for flood season in 2013(June to September) for Tonghe Station

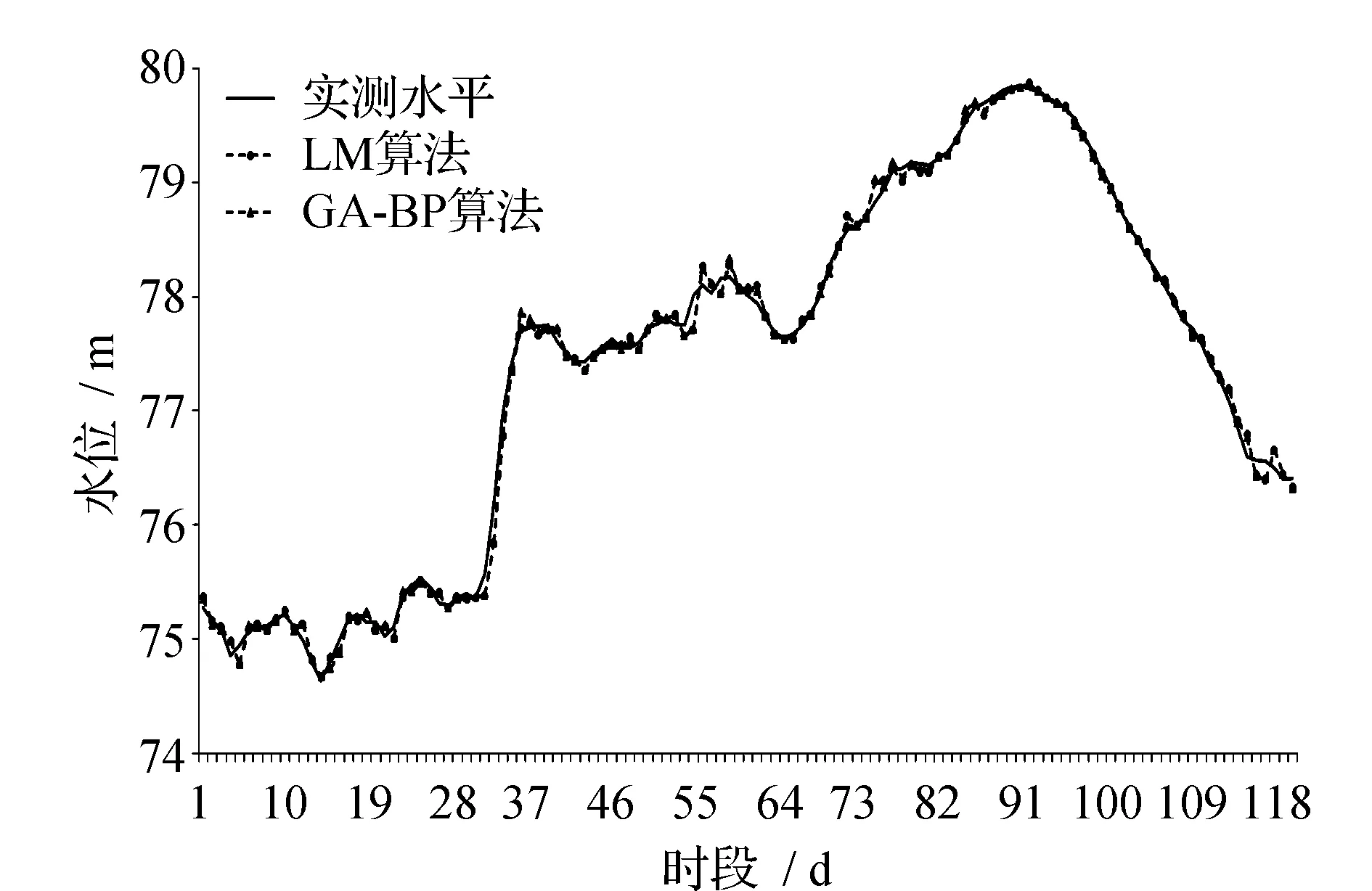
图5 佳木斯站2013年汛期(6—9月)水位过程预报检验Fig.5 Verifying the validity of water-level forecasting for flood season in 2013(June to September) for Jiamusi Station

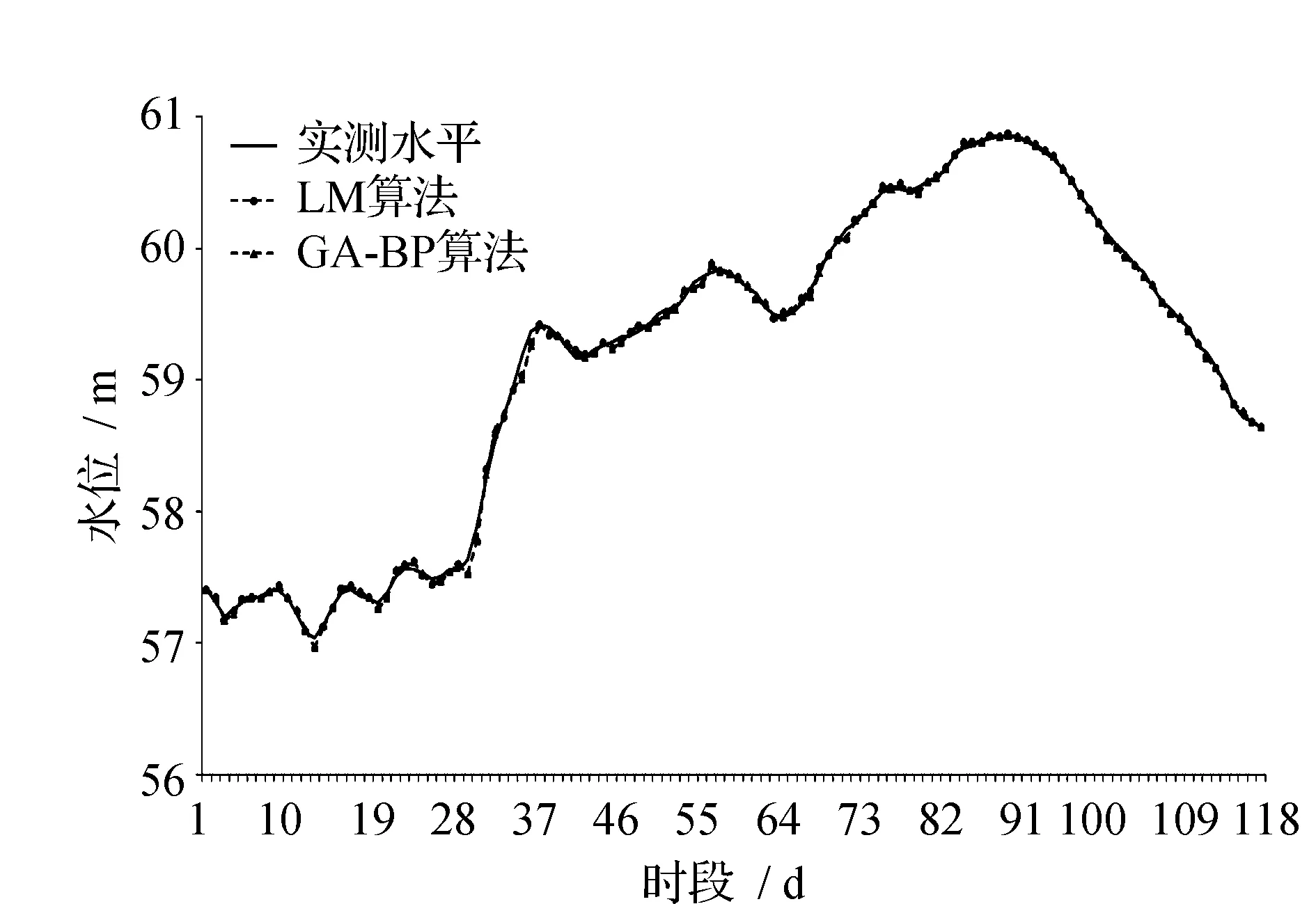
图6 富锦站2013年汛期(6—9月)水位过程预报检验Fig.6 Verifying the validity of water-level forecasting for flood season in 2013(June to September) for Fujin Station

3 结 论

人工神经网络在洪水预报中应用前景广阔，但是从众多的神经网络中选取最适合建立洪水预报模型的算法很困难。本文以松花江干流的水位为研究对象，考虑到假定基面的变化对水位观测值的影响，因此各站均采用水位涨差来作为模型输入，选取基于LM算法和基于遗传算法优化的BP神经网络建立水位预报模型。从预报结果分析，所有5个代表站点2种算法的预报合格率>90%，确定性系数>0.99，预报精度均能达到甲等。说明两种优化后的BP算法在收敛速度和预测精度上均取得较好的效果，能够有效地避免BP网络陷入局部极小值。且GA-BP算法各性能评价指标均略优于LM算法，预报结果较为稳定，表明遗传算法能有效优

化BP网络初始权值和阈值，最适合用于建立水位预报模型。而在对精度要求不高的情况下，简单的方法要优于复杂的。因此，一般情况下，LM算法的预报精度满足预报要求，可以用于松花江干流水位预报。

[1]陆志华,夏自强,于岚岚,等.松花江干流中游段径流年内分配变化规律[J].河海大学学报:自然科学版,2012, 40(1): 63-69.

[2]侯 翔,汤元斌,刘笃晋,等.三种神经网络在洪水预报中应用的比较[J].计算机系统应用, 2013, 22(12): 35-38.

[3]李云良,张 奇,李 淼,等.基于BP神经网络的鄱阳湖水位模拟[J].长江流域资源与环境,2015, 24(2): 233-240.

[4]阎平凡,张长水.人工神经网络与模拟进化计算[M].北京：清华大学出版社.

[5]苑希民,李鸿雁.人工神经网络与遗传算法在河道洪水预报中的应用[J].水利发展研究,2002,2(12):50-55,58.

[6]翟宜峰,李鸿雁,刘寒冰,等.用遗传算法优化神经网络初始权重的方法[J].吉林大学学报:工学版, 2003, 33(2): 45-50.

[7]Van Rooij A J F, Jain L C, Johnson R P. Neural network training using genetic algorithms[M]. Singapore: World Scientific, 1996.

[8]SL250-2000,水文情报预报规范[S].

[9]Sezin T, Peggy A, Johnson A. Rainfall-runoff modeling using artificial network[J]. Journal of hydrology engineering, 1999,(7):232-239.

Application of the improved BP neural networks in water-level forecasting for mainstream of Songhuajiang River

LIU Wen-Bin1，ZHAO Si-Yuan2，HAO Zhen-Chun2,*，WANG Mao-Mei3，MA Xi-Rong4,NIMA Dan-Zeng5

(1.Hydrological Bureau of Heilongjiang Province, Harbin 150001, China；2.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering,Hohai University, Nanjing 210098, China；3.Jiangsu Hydraulic Research Institute, Nanjing 210017, China；4.Pearl River Hydraulic Research Institute, Guangzhou 510611, China; 5.Shannan Branch of the Tibet Autonomous Region Hydrology Bureau,Shannan 856000,Tibet,China)

Water-level of mainstream of Songhuajiang River has a nonlinear response to the upper river discharges and the regulation and storage capacity of reservoir, the three-layer back propagation neural network has the ability to simulate water level for 5 representative hydrological observation stations in the mainstream of Songhuajiang Rvier, including Zhaoyuan Station, Harbin Station, Tonghe Station, Jiamusi Station, and Fujin Station. Based on slow convergence of learning, difficulty selecting of parameters and liability of dropping into local minimum for BP neural networks, the outcomes of these models is analyzed and compared, by establishing water-level forecasting models based on the Levenberg-Marquart algorithm and the genetic algorithm respectively. It shows both algorithms all have the fast convergence and excellent performance in forecasting water-level. Especially for that the paper join the genetic algorithm which is good in global searching and BP algorithm which is effective on accurate local searching together and supplementing mutually, the method has a good application prospects.in water-level forecasting field.

BP neural network; Levenberg-Marquart algorithm; genetic algorithm; water-level forecasting

10.13524/j.2095-008x.2015.04.055

2015-09-16

国家自然科学基金资助项目(41371047)；中国科学院战略性先导科技专项(XDA05110102)；水文水资源与水利工程科学国家重点实验室专项经费(1069-514031112)

刘文斌(1975-)，男，黑龙江鹤岗人，工程师，研究方向：水文预报，E-mail:hljlwb@eyou.com;*通讯作者：郝振纯(1958-)，男，山西翼城人，教授，博士研究生导师，研究方向：水文水资源和气候变化影响，E-mail: hzchun@hhu.edu.cn。

P338

A

2095-008X(2015)04-0006-06