轨道静态检测轨向高低新算法及精度研究

2015-03-17郑伦英岑敏仪

铁道勘察 2015年1期

关键词：测站全站仪静态

郑伦英　岑敏仪　王　磊

(1.中铁工程设计咨询集团有限公司，北京　100055；2.西南交通大学，四川成都　610031)

Research on the New Algorithm and Precision in Track Static Detecting of Track-alignment

ZHENG Lun-ying　CEN Min-yi　WANG Lei

轨道静态检测轨向高低新算法及精度研究

郑伦英1岑敏仪2王磊1

(1.中铁工程设计咨询集团有限公司，北京100055；2.西南交通大学，四川成都610031)

Research on the New Algorithm and Precision in Track Static Detecting of Track-alignment

ZHENG Lun-yingCEN Min-yiWANG Lei

摘要基于自动跟踪、自动照准功能的全站仪和轨道测量仪轨道静态检测技术已广泛应用于普速铁路和高速铁路的建设运营中。目前相关规范只对轨道静态检测的自由设站精度和轨道几何参数限差进行了规定，未对轨道几何参数的测量精度进行相关说明。基于轨道静态检测自由设站的设站误差和全站仪的观测误差，提出并推导利用轨道点横向、垂向偏差，计算轨向、高低的新算法及其精度模型。研究表明，使用标称精度为0.5″的全站仪施测，可满足轨道静态检测的精度要求。

关键词轨道静态检测自由设站轨向高低测量中误差

通过轨道静态检测获得的实测轨距、水平(超高)、线路中线坐标和高程、左右轨轨面坐标和高程，与线路相应里程处的设计状态相比较，即可得轨道的轨距偏差、水平(超高)偏差、扭曲、轨向和高低，以此判断轨道的平顺性，进而指导轨道调整。根据现有相关规范规定，轨道静态检测的测量方法是结合全站仪自由设站和极坐标法测量，自由设站的精度为X、Y、Z三方向的中误差≤0.7 mm，定向角精度≤2″；每一测站的最大测量距离不宜大于80 m；无砟轨道的测量步长宜为一个扣件距离，有砟轨道不宜大于2 m，相邻测站重复观测6～10根轨枕[1]。而规范对轨道几何参数只进行了限差要求，并没有规定其测量精度。从测量的理论基础出发，评定一种测量方法的可行性，需参考其性能指标的中误差。基于此，提出利用轨道点横向、垂向偏差，计算轨向、高低的新算法，并通过编程验证此算法的正确性；其次，基于该新算法，从全站仪自由设站和极坐标法测量原理出发，推导轨向、高低的精度模型；最后，基于规范规定的自由设站精度和最远观测距离，结合不同的全站仪观测精度，计算得出轨向、高低的测量中误差。研究表明，使用标称测角精度为0.5″的全站仪能满足轨道静态检测精度。

1绝对测量的极坐标模型

轨道静态检测的绝对坐标测量是基于全站仪自由设站得出的设站坐标，再利用极坐标法测量获得站内轨道点棱镜中心的坐标和高程，如图1所示。

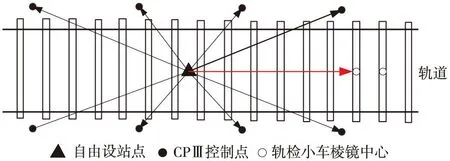
图1　基于全站仪和轨道测量仪的轨道静态检测测量

如图1所示，高速铁路无砟轨道静态检测的设站坐标是基于CPⅢ控制网的自由设站获得，设全站仪的设站坐标为(XS，YS，ZS)，定向角为w，全站仪观测量为斜距S、天顶距β和水平方向L，根据极坐标法计算轨道点棱镜中心的三维坐标为

(1)

式中，(XP，YP，ZP)——测站内某轨道点P棱镜中心的三维坐标。

轨道中线坐标计算的实质是将轨道测量仪棱镜中心坐标经坐标转换转化为相应线路中线的坐标，轨道测量仪的内部误差对每个轨道点的影响大致相同，可不予考虑。在分析轨道点平面点位中误差和高程中误差时，只需考虑设站误差和观测误差，其中设站误差包括平面点位中误差M0、高程中误差σZ和定向角中误差w，观测误差包括距离、水平方向和天顶距中误差(σS，σL，σβ)。根据公式(1)可得轨道点平面点位中误差MP为

(2)

式中，σα——表示方位角中误差，由定向角中误差和水平方向中误差构成。

轨道点高程中误差MZ为

(3)

2轨向和高低计算的新方法

轨道静态检测中，轨向和高低是根据轨道点的实测、设计三维坐标，计算相应弦长的实测、设计正矢和矢高，以此得出轨道点10 m、30 m和300 m弦长的轨向和高低值。该方法计算过程复杂且不能直观反映轨道偏移量对轨道平顺性的影响，不便于后续轨道调整量的计算和分析。提出利用轨道点横向、垂向偏差，计算轨向、高低的新算法。

所谓轨道点横向偏差，即实测轨道点和其在设计线路上投影点的距离，以实测点在线路左为正，在设计线路右为负(如图2所示)，点P′为实测轨道点，在设计线路上的投影点为P，(ΔX，ΔY)表示轨道点P在线路坐标系下的设计坐标与实测坐标的差值，则轨道点P的横向偏差f为

(4)

同轨向横向偏差计算原理相同，轨道的垂向偏差g如图3所示，计算公式为

(5)

式中ΔZ——轨道点设计高程减实测高程；

αP——轨道点的纵向方位角。

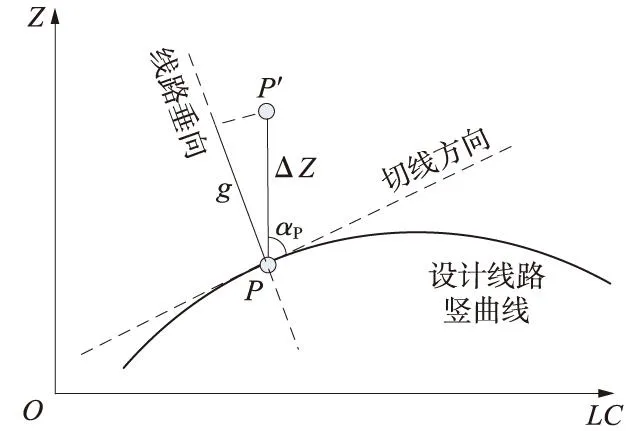
图3　轨道点垂向偏差

2.1　10 m弦检测方法

根据10 m弦轨向、高低的计算原理可知：轨向、高低的计算，涉及弦线中间的轨道点、弦线的起始和结束点，利用轨道点横向和垂向偏差计算轨向、高低的公式为

2.2　30 m弦检测方法

根据30 m弦轨向、高低的计算原理可知：轨向、高低的计算涉及检测点和其对应检核点(相隔5 m)、弦线的起始和结束点。如图4所示，利用横向偏差计算轨向的公式为

(6)

式中S2——近似表示为轨道点2到轨道点1的里程差值；

S3——近似表示为轨道点3到轨道点1的里程差值。

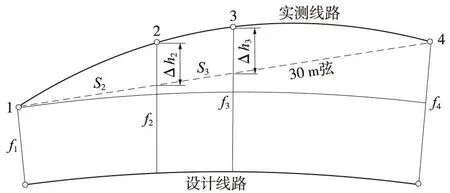
图4　使用横向偏差计算30 m弦轨向平顺性

同理，使用垂向偏差计算高低的公式为

(7)

2.3　300 m弦检测方法

使用横向、垂向偏差，计算轨道点300 m弦的轨向、高低值的不同之处在于弦线长度为300 m，检测点和其对应点之间的距离为150 m。因此，300 m弦轨向、高低的计算公式为

(8)

(9)

选取某高铁线路中一段轨道静态检测的测量数据，其平曲线半径最小为3 500 m，竖曲线半径为30 000 m。编程实现轨向、高低的理论计算方法和文章提出的新算法，通过对比分析，10 m、30 m和300 m弦的轨向、高低值，两种方法的计算结果之差最大不超过0.1 mm，由此可知，利用轨道点横向、垂向偏差，计算轨向、高低的方法可行。

3轨向的精度分析

根据式(2)可知，轨道点平面点位误差由设站误差、全站仪测距误差和测角误差组成。而在以线路中线和轨道横断面为极轴的局部坐标系中，平面点位误差可以分为轨道横断面上的误差ML和纵断面的误差MD，如图5所示。根据轨道静态检测的外业测量要求，全站仪需架设在线路中线位置，且线路曲线半径都很大，则全站仪与轨道测量仪棱镜中心的连线大致垂直于线路的横断面，因此全站仪的测距误差和天顶距误差对ML的影响可以忽略不计，则轨道点横向中误差可表示为[2]

(10)

图5　轨道点点位误差

以30 m弦轨向为例，根据式(6)可知，轨道点30 m弦的轨向计算涉及四个轨道点1、2、3、4，考虑相邻测站A和B的搭接测量，每个轨道点可位于一个测站或两个测站的搭接段内，其分布情况为：

①轨道点1、2、3、4均位于一个测站内。

②轨道点1、4分别位于测站A和B，点2、3位于搭接段。

③轨道点2位于搭接段，点1位于测站A，点3、4位于测站B。

④轨道点3位于搭接段，点1、2位于测站A，点4位于测站B。

设测站A和B的设站误差分别为mA和mB，定向角误差分别为wA和wB，当轨道点1、2、3、4均位于测站A时，则四个轨道点的横向误差Δi可表示为

根据式(6)和上述四个式子可得轨道点2的轨向误差为

(11)

根据上式可得轨道点2的30 m基线轨向测量中误差为

(12)

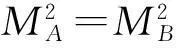
按照上述计算方法，同理可得另外三种情况的轨道点轨向精度，如表1所示。

表1　30 m弦轨向测量中误差情况　mm

根据《高速铁路工程测量规范》可知， 30 m弦轨向不平顺性的允许偏差为2 mm，取三倍中误差为测量的极限误差，则30 m弦轨向的必要测量精度为0.63 mm[4]。根据上表可知：

①当使用标称测角精度1″的全站仪进行轨道静态检测时，在一部分点位分布情况下无法满足其测量的必要精度，建议使用标称测角精度为0.5″的全站仪进行轨道静态检测。

②当四个轨道点处于同一个测站时，全站仪观测误差是影响轨向精度的主要因素；当轨道点处于搭接段，存在设站误差影响时，设站误差是影响轨向精度的重要因素。

同理可分析10 m和300 m弦轨向精度，在这里不做具体阐述。

4高低精度分析

参照轨向的精度分析原理，根据公式(2)和公式(7)，可对轨道高低精度进行研究。以30 m弦高低为例，四个轨道点分布情况同30 m弦轨向精度分析时相同，当轨道点1、2、3、4位于同一个测站内，使用1″等级的全站仪时，σβ=±2″，MΔh=0.93 mm；使用0.5″等级的全站仪时，σβ=±1″，MΔh=0.46 mm。

按照上述计算方法可得另外三种情况的轨道点高低精度，如表2所示。