爆炸荷载作用下城市桥梁动态响应及其损伤过程分析
2015-03-17朱劲松
朱劲松,邢 扬
(1. 天津大学建筑工程学院,天津 300072;2. 滨海土木工程与安全教育部重点实验室(天津大学),天津 300072)
爆炸荷载作用下城市桥梁动态响应及其损伤过程分析
朱劲松1, 2,邢 扬1
(1. 天津大学建筑工程学院,天津 300072;2. 滨海土木工程与安全教育部重点实验室(天津大学),天津 300072)
摘 要:为了对人流、车流密集的城市市政桥梁进行合理的抗爆设计和爆炸风险评估,提出了爆炸荷载作用下城市桥梁动态响应与损伤过程分析的数值方法.首先,通过对城市桥梁爆炸风险源的分析,确定城市桥梁可能遭遇的爆炸源类型及爆炸荷载工况.然后,基于大型通用有限元软件ANSYS/LS-DYNA建立桥梁、炸药和空气三者的有限元模型,分别选择JWL(Jones-Wilkins-Lee)状态方程与线性多项式状态方程对炸药和空气模型进行定义,选用ALE(arbitrary Lagrange-Euler)算法模拟爆炸冲击波在空气中的传播;通过改变炸药的安放位置和质量,得到爆炸荷载作用下桥梁关键部位的位移响应、Von-Mises应力分布和整个桥梁的破坏形态,并模拟爆炸后桥梁的损伤过程;以Tuler-Butcher损伤累积准则为依据,求得某些指定单元在不同爆炸距离和不同TNT当量下的损伤累积曲线.最后,以一座大型钢桁架拱桥为例说明本文提出的方法的计算过程,其计算结果可作为桥梁抗爆设计和爆炸风险评估的依据.
关键词:爆炸荷载;ALE算法;钢桁架拱桥;动态响应;数值模拟
作为陆地交通咽喉的桥梁,在军事交通和国民经济中均具有至关重要的地位和作用.然而,战争和偶然事故所引发的城市桥梁爆炸事故也越来越严重.我国虽然恐怖袭击很少,但是战争的威胁目前仍然存在,并且易燃易爆化学品的爆炸也会对城市桥梁和人民生命财产造成损害.2007年4月29日凌晨,连接美国旧金山和奥克兰的高速公路发生油罐车爆炸事故,造成一座跨海大桥的引桥倒塌.2013年2月1日上午9时许,一辆运输烟花爆竹的大货车行至连霍高速公路河南三门峡市渑池段义昌大桥时发生爆炸,造成该桥南半幅桥面垮塌,部分车辆和人员坠落桥下,事故共造成26人死亡.由于国内外城市桥梁爆炸事故的频繁发生,对城市桥梁抗爆方面的研究已受到国内外研究人员和工程设计人员的广泛重视.然而,现阶段虽然在桥梁设计原则中有抗风、抗震、桥墩防撞[1]等明文规范,但并没有涉及到抗爆方面的设计要求.因此,研究爆炸荷载作用下城市桥梁的动态响应及其渐进失效机理,为城市桥梁的抗爆风险评估提供参考与支撑,在军事和民用等方面均具有极其重要的意义.
由于爆炸作用时间极短,因此极难得到精确的计算分析结果.实验方法又耗资过于巨大,且危险性很大.与爆炸实验相比,由于数值模拟方法的花费较少、无需动用大量的人力物力,并且能较好地模拟出结构在爆炸荷载作用下的动态响应,因此数值模拟方法在桥梁抗爆研究中被广泛采用,常用的爆炸数值模拟软件有ANSYS/LS-DYNA、FLACS、DYTRAN和ABAQUS等.Winget等[2]在总结爆炸荷载对结构影响现有成果的基础上,研究了桥下爆炸时净空高度等几何参数对爆炸破坏的影响.Fujikura等[3]通过简化分析和1/4模型试验,研究了钢管混凝土柱式桥墩的抗爆性能及其破坏特征.Gannon[4]利用软件CONWEP分析了不同类型的炸弹分别在桥上和桥下爆炸时,桥梁类型、跨度、桥面板厚度等因素对桥梁在爆炸荷载作用下的动态响应的影响.邓荣兵等[5]对爆炸荷载作用下某大跨度斜拉桥的动态响应及其桥面板的损失特征进行了数值模拟;张开金[6]基于ANSYS/LS-DYNA软件模拟了爆炸载荷作用下钢筋混凝土桥梁的失效过程;蒋志刚等[7]采用数值模拟方法研究了空中爆炸冲击波作用下悬索桥竖向弯曲响应. Tang等[8]和Hao等[9]运用ANSYS/LS-DYNA软件,分析了某大跨斜拉桥在汽车炸弹爆炸冲击作用下桥塔、桥墩和桥面结构的局部破坏以及桥梁的整体倒塌.综上所述,虽然国内外有关爆炸荷载特性的研究已取得较多成果,但对城市桥梁爆炸风险源和爆炸荷载类型未能合理确定,对城市桥梁结构抗爆研究的范围和对象明显不足.
为了对人流车流密集的城市市政桥梁进行合理的抗爆设计和爆炸风险评估,笔者采用数值模拟方法,首先通过对城市桥梁爆炸风险源的分析,确定城市桥梁可能遭遇的爆炸源类型及爆炸荷载工况;然后基于大型通用有限元软件ANSYS/LS-DYNA建立了钢桁架拱桥、炸药和空气的有限元模型,分别采用JWL(Jones-Wilkins-Lee)状态方程和多项式状态方程定义炸药和空气模型,采用ALE(arbitrary Lagrange-Euler)算法模拟爆炸冲击波在空气中的传播,模拟炸药爆炸后整个桥梁结构的动态响应、渐进失效机理与损伤破坏路径,以及爆炸空气冲击波在空气中的传播规律.通过改变炸药的安放位置和质量,得到爆炸荷载作用下桥梁关键部位的位移响应、Von-Mises应力分布和桥梁局部破坏形态,并模拟桥梁在爆炸后的局部损伤过程.以Tuler-Butcher理论为依据,求得某些指定桥梁单元在不同爆炸距离和不同TNT当量下的损伤累积曲线.分析结果可以为桥梁抗爆设计和爆炸风险评估提供参考.
1 城市桥梁爆炸风险源
城市桥梁所面临的爆炸威胁主要有两个方面:一是战争时期,桥梁有可能遭受到如炸弹、导弹等军用武器的打击;二是和平时期,桥梁可能遭受到运输各种危险品的车辆爆炸事故和恐怖袭击,这是本文对城市桥梁面临的潜在爆炸风险源分析的重点.
危险货物的运输被视为“流动的危险源”,相比于恐怖炸弹,运输易燃易爆物品的罐车或者槽车发生爆炸将会造成更严重的后果.常用运输易燃易爆物品的车辆发生爆炸时的TNT当量一般为4,000~30,000,kg[10].
恐怖炸弹的种类主要分为邮件炸弹、箱包炸弹、人体炸弹和汽车炸弹等.其中邮件炸弹、箱包炸弹和人体炸弹等所携带的炸药量相对较少,通常在几至几十千克TNT当量范围内.而汽车炸弹因为载药量大且不容易被发现,是袭击民房、桥梁等公共设施最常用的方式.
分析近年来易燃易爆物品运输爆炸事故和恐怖炸弹袭击案件,得到不同车型的汽车炸弹TNT当量及爆炸高度大致范围见表1[11].

表1 常见汽车炸弹TNT当量及爆炸高度Tab.1 Common car bomb TNT equivalence and blast height
2 算法理论和材料模型
2.1ALE多物质流固耦合算法
在爆炸数值模拟中,算法种类很多,其中Lagrange、Euler与ALE是最常用的3种算法,3种算法各有优势,但由于ALE算法包含了Lagrange算法和Euler算法的众多优点,因此在数值模拟中最为常用[12].
2.1.1 ALE算法基本原理
ALE算法中,材料网格与Lagrange坐标相对应,空间网格与Euler坐标相对应,且存在区别于这两种网格的参考坐标系.ALE描述的物质导数[13]为

式中:f为物理量;Xi为质点X的拉格朗日坐标;vi为质点X的速度,m/s;wi为参考点x的速度,m/s.
爆轰产物与空气均可认为是无黏性的物质,所以可通过物质导数关系,把用Euler方法描述的控制方程转换为用ALE算法描述的控制方程[14],即质量守恒方程
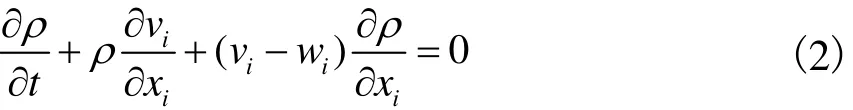
动量守恒方程

能量守恒方程
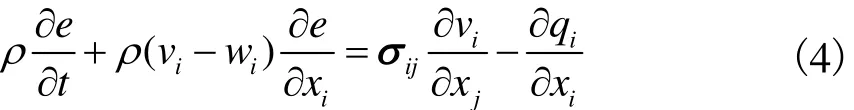
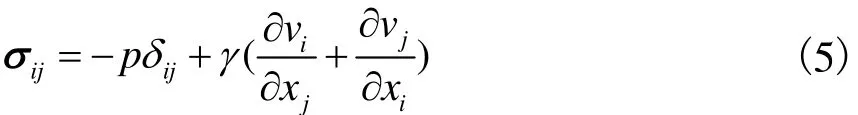
式中:ij为柯西应力(Cauchy stress)张量;r为材料密度,kg/m3;p为爆轰压力,Pa;g为动态黏度系数;e为单位体积内能,J/m3ijd为Kronecker函数,其表达式为

方程组(2)~(4)可通过状态方程和边界条件求解.
2.1.2 多物质单元
ALE算法分为单物质ALE算法和多物质ALE算法.所谓单物质算法,就是一个单元只能对应一种材料,而多物质算法就是一个单元中允许对应两种以上的材料.本文所采用的算法为多物质ALE算法.
2.1.3 流固耦合作用方式
流固耦合主要有共用节点和使用关键字定义两种分析方法,其中共用节点法由于限制流体运动,容易使网格发生变形,从而出现体积为负数的情况,给数值计算造成极大的困难[15],因此在爆炸冲击下结构大变形模拟中较少使用.使用关键字定义法很好地避免了共用节点法所存在的各种缺点,且考虑了流固之间的相互作用问题,因此使用关键字定义法在爆炸荷载作用下的流固耦合分析中最为常用.本文采用使用关键字定义的方法来进行流固耦合分析.
2.2材料模型
2.2.1 空气材料模型
空气的状态方程采用线性多项式状态方程[15]表达式,即
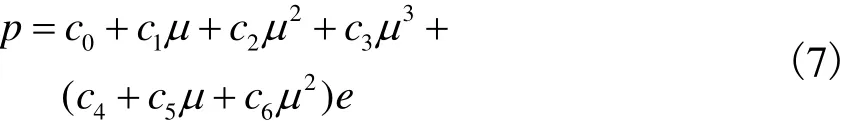
式中:m=1/U-1,U为空气的相对体积,U=u/u0,u为爆炸后空气的体积,m3,u0为空气初始体积,m3;ci(i=0,1,2,…,6)为多项式各项系数.U和e的初值分别为U0、e0,其中U0取1.0.当线性多项式状态方程用于表达空气模型时,各参数取值[16]见表2.

表2 空气状态方程参数Tab.2 Parameters of air state equation
2.2.2 炸药材料模型
炸药爆炸是一个复杂的化学反应过程,爆轰过程与爆炸物种类、属性、参数等密切相关.在数值模拟过程中,点火生长模型与高能燃烧模型[11]是最常用的两种模拟炸药的模型.但是,采用点火增长模型时,需要用到很多状态方程,从而需要定义大量的参数,可这些参数要通过大量实验来得到,一般不容易得到,因此本文采用高能燃烧模型.假定炸药类型为TNT炸药,爆炸材料具体参数为:炸药密度r=1,714,kg/m3,爆轰速度v=7,967,m/s,爆轰波波阵面(Chapman-Jouguet,CJ)压力为2.86×104,MPa.
采用高能燃烧材料模型时,其相应的状态方程为JWL方程,其等熵方程为

式中:V为炸药的相对体积,V=v/v0;v为爆轰产物体积,m3;v0为炸药初始体积,m3;其中初始相对体积V0取1.0;E0为炸药单位体积的初始能量,J/m3;A、B、R1、R2和w为与炸药性质有关的常数,通常由实验确定.各参数的值[17]见表3.

表3 JWL状态方程参数Tab.3 Parameters of JWL state equation
2.2.3 桥梁结构材料模型
桥梁结构材料常采用混凝土与钢材,在数值模拟过程中,常采用弹塑性硬化(plastic-kinematic,PK)材料模型来模拟桥梁结构的材料.用PK材料模型来模拟桥梁材料时,其应变率采用Cowper-Symonds[15]模型.PK材料模型的表达式为
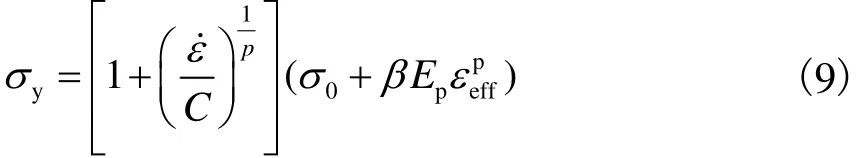
式中:sy为动态屈服应力为应变率,为有效塑性应变为初始屈服应力,Pa;C为参数;Ep为塑性硬化模量,Pa,定义为,其中E为弹性模量,Pa,Etan为切线模量为材料硬化参数,当时,为随动硬化;当时,为混合硬化;当时,为各向同性硬化.
3 算例概况
3.1桥梁概况
以国内某城市中心区主干道一座跨河的大型钢桁架组合拱桥为例来说明本文数值计算方法的分析过程.该桥为钢桁架拱桥,全长396,m,主跨为13.17,m+146.0,m+13.21,m=172.38,m.桥宽31.5米,拱宽24.5,m,弦拱距离桥面高26,m,下弦拱距桥面高22,m.桁式拱肋的上下弦杆为1.0,m(高)× 1.0,m(宽)的焊接箱型断面;中间腹杆为采用0.95,m(高)×0.6,m(宽)的工字形断面;中跨拱结构矢高为31.924,m、矢跨比为1∶4.57.全桥共计30根吊杆,间距为8,m,均为PE护层高强钢丝索,其强度为1,670,MPa.钢箱梁采用1.8,m(高)×1.0,m(宽)的焊接箱型断面;钢桥面采用正交异型板桥面;人行道挑臂长度为3,m;钢材型号为Q345qD.桥梁整体布置如图1所示.

图1 桥梁整体布置Fig.1 General arrangement of bridge
3.2有限元模型
爆炸物用等效的TNT炸药代替,炸药尺寸为1,m×1,m×1,m,空气域尺寸为200,m×40,m×50,m.空气、炸药与桥梁空间几何模型如图2所示.建立的有限元模型中,空气和炸药单元均采用8节点实体单元(SOLID164).桥梁吊杆采用3节点3D圆杆单元(LINK160),钢板采用4节点薄壳单元(SHELL 163).采用了两种尺寸的网格,炸药点周围10,m范围内网格尺寸为50,mm,其他地方网格尺寸为80,mm,两种精度网格之间有2,m的过渡区域.炸药和桥梁的有限元模型如图3所示.
3.3计算工况
该桥为中承式拱桥,箱梁与桥墩之间为刚性连接,考虑到跨中截面弯矩和挠度最不利位置以及拱梁结合部位在拱桥中的关键作用,假定炸药分别在桥梁两个典型位置(见图1)爆炸,位置1为桥梁跨中偏右侧吊杆的最外侧车道;位置2为桥梁拱梁结合部位最外侧的车道.其中最外侧车道中心距桥梁轴线6.4,m.各计算工况JWL状态方程参数见表4.

图2 空气、炸药与桥梁空间三维结构模型Fig.2 Three-dimensional structural model of air,dynamite and bridge

图3 炸药和桥梁有限元模型Fig.3 Finite element model of bridge and dynamite

表4 计算工况Tab.4 Calculation cases
通过对比工况1~3来研究不同高度下桥梁的动态响应,通过对比工况4~6来研究不同TNT当量下桥梁的动态响应,工况7和8用来模拟桥梁受到严重损毁的情况.
4 模拟结果及动态响应分析
4.1爆炸冲击波的传播规律
炸药爆炸后,会在瞬间转化为高温高压的气态爆轰产物,并迅速向四周扩散,挤压周围空气,导致周围空气的压力和温度也进一步上升,从而高温高压的范围进一步扩大,最终形成爆炸冲击波.随着爆炸冲击波的不断传播,超压范围不断扩大,爆轰压力却逐渐减小,减小的速度也越来越慢[18].在工况1中,沿着炸药右侧每隔4,m取1个空气单元,图1(a)中给出了所选取的空气单元的编号(AE1~AE5)及位置,图4为所选各空气单元的超压时程曲线,AE1~AE5空气单元的超压峰值的大小和出现时刻分别为5.49,MPa、3.29,MPa、1.97,MPa、1.18,MPa、0.71,MPa 和0.48,ms、0.57,ms、0.65,ms、0.75,ms、0.84,ms,由此可见,与起爆点距离越远,爆炸冲击波达到超压峰值的时间越晚,超压峰值越小.
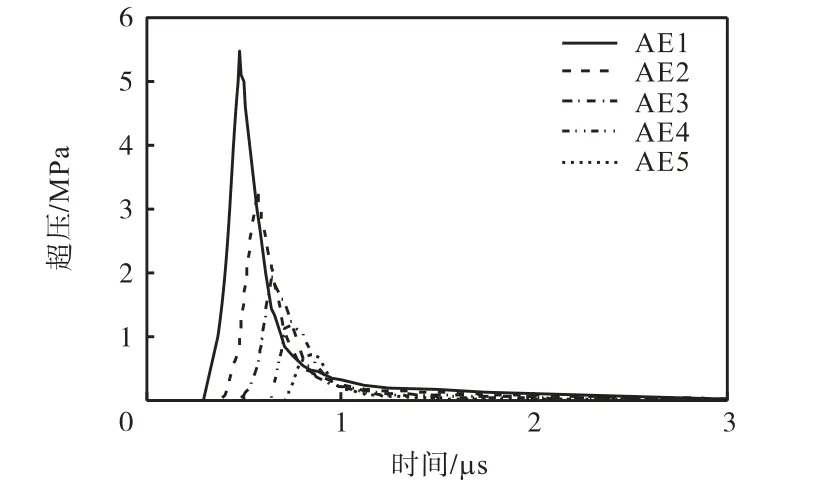
图4 空气单元的超压时程曲线Fig.4 Over pressure time history curves of air elements
在工况1中,沿桥梁纵向选取桥面上距炸药4~8,m范围内的3个单元,图1(b)中给出了所选取的桥梁单元的编号(BE1~BE3)及位置,图5为所选桥梁单元的超压时程曲线.分析这3个单元的超压时程后发现,与起爆点距离越近,单元上的爆轰压力达到峰值的时间越早,数值越大,从而单元越有可能发生失效.
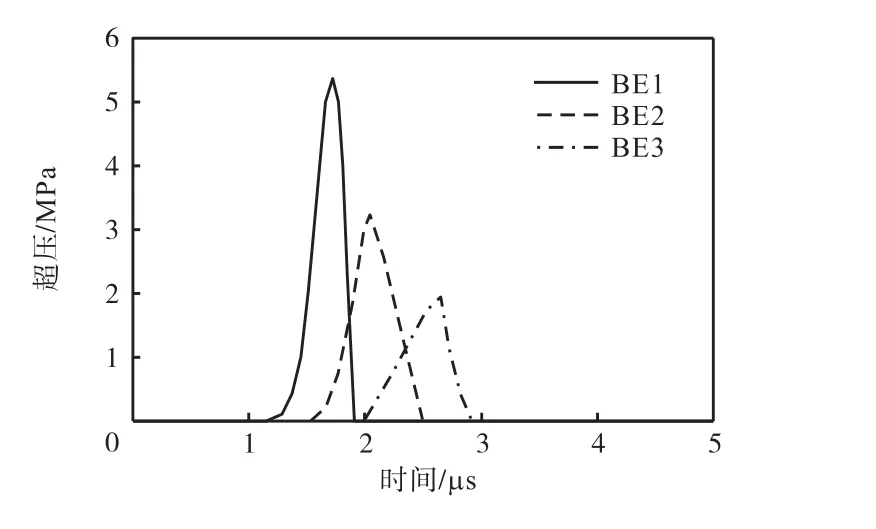
图5 桥梁单元的超压时程曲线Fig.5 Over pressure time history curves of bridge elements
4.2爆炸荷载下桥梁的动态响应
在工况1中,从位于炸药正下方的桥梁节点起,沿着桥梁的纵轴方向每2,m取1个节点,图1(b)中给出了所选取的桥梁节点的编号(BN1~BN5)及位置,该组节点在爆炸发生后前15,ms内z轴竖向位移时程曲线如图6所示,可以看出桥梁顶板产生的最大竖向位移出现在炸药正下方的位置(即跨中),该节点的位移在15,ms时大约为-17.92,mm,而在距离炸药正下方位置8,m处节点的位移可近似认为是0.可见,当炸药量较小时,爆炸只会对炸药周围的桥梁局部造成损伤,不会对桥梁产生整体破坏.

图6 桥梁节点竖向位移时程曲线Fig.6 Vertical displacement time history curves of bridge nodes

图7 工况1下跨中区域Von-Mises应力分布Fig.7 Von-Mises stress distribution near the mid-span at working condition 1
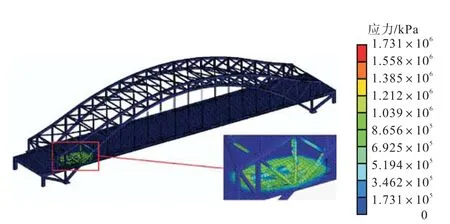
图8 工况4下拱梁结合部位Von-Mises应力分布Fig.8 Von-Mises stress distribution near the connection area of beam and arch at working condition 4
图7为工况1中跨中区域的Von-Mises应力分布,图8为工况4中拱梁结合部位的Von-Mises应力分布.从两图中可以看出,桥梁结构的Von-Mises最大值达到了1,731,MPa,因此在距离炸药位置较近的局部范围内,单元上所受到的爆轰压力的大小远远超过了桥梁所用钢材Q345qD的屈服应力(345,MPa),材料发生了永久性变形,该单元就可认为失效,且脱离桥梁整体模型.由于与炸药的距离最近,所以炸药正下方的桥梁顶板最早发生破坏,且破坏最为严重.
5 爆炸荷载作用下桥梁的损伤过程分析
5.1损伤机理
爆炸可能引发桥梁产生多种形式的破坏.破坏的形式和程度主要取决于炸药类型、桥梁的抗爆能力和桥梁结构类型等.普遍来说,发生爆炸后桥梁可能产生的破坏形式主要可分为整体破坏和局部破坏两种.当足量的炸药在距离桥梁所在地较远处发生爆炸时,桥梁结构将在爆炸荷载作用下发生整体破坏,桥梁上的全部构件都将由于爆炸冲击波的作用而内力增大.但因为爆炸发生地距离桥梁较远,爆炸冲击波传播到桥梁所在地时其波阵面范围已经很广,桥梁整体各部位所受爆轰压力的数值变化不大,所以此时可假设作用在整座桥梁上的爆轰压力为一定值.当少量的炸药在距离桥梁所在地较近处发生爆炸时,桥梁整体各部位所受爆轰压力的数值差别极大,不可再假设爆轰压力为一定值,而需按变量来考虑,此时桥梁发生的破坏为局部破坏.若发生局部破坏的位置为桥梁的关键位置,则桥梁有可能会因关键构件的失效而发生整体破坏.
5.2基于Tuler-Butcher损伤累积准则的损伤分析
爆炸损伤分析属于损伤力学的研究范围.Tuler-Butcher损伤累积准则是Tuler和Butcher[19]在1968年提出的一种积分型准则,相比于“离散型”损伤累积准则,其实现了对于损伤累积的连续测量,不足之处是该准则只能在宏观力学范围内使用.但因为Tuler-Butcher损伤累积准则在工程中使用方便,且便于理解,因而在实际中被广泛应用[20].其形式[21]为

式中:th为材料的损伤阈值应力;(t )为损伤面上的拉应力;tc为荷载作用下材料发生损伤的所需时间;、为材料参数.当1=时,式(10)为冲量准则;当=2时,式(10)为能量准则.
损伤因子D的表达式为

图9是工况1~3下炸药正下方桥梁单元的超压时程曲线.该曲线表明,同等TNT当量的情况下,当爆炸高度分别为0.5,m、0.7,m和0.9,m时,单元所受的超压峰值的大小分别为-140.79,MPa、-120.26,MPa 和-81.32,MPa;爆炸高度从0.5,m增加到0.9,m时,超压的峰值减少了42.24%.可见,爆炸距离越近,单元所受的超压峰值越大.由于爆炸后空气冲击波遇到了与之垂直的桥面,在桥面处空气质点的速度骤然增大,达到一定程度时,就要向相反方向反射,于是形成了反射冲击波.在入射冲击波和反射冲击波的作用下,便出现了两个峰值,但由于能量损失的缘故,反射冲击波所产生的峰值大小仅为入射冲击波产生的峰值大小的30%~50%.
以Tuler-Butcher损伤累积准则为依据,得到对该单元在不同爆炸高度下的损伤累积曲线,如图10所示.由图10可见,爆炸距离越近时,累积损伤因子越大,即损伤越严重.
以Tuler-Butcher损伤累积准则为依据,得到对该单元在不同爆炸高度下的损伤累积曲线,如图10所示.由图10可见,爆炸距离越近时,损伤因子越大,即损伤越严重.

图9 不同爆炸高度下炸药正下方桥梁单元的超压时程曲线Fig.9 Over pressure time history curves of the bridge element just below the dynamite under different blast height

图10 不同爆炸高度下炸药正下方桥梁单元的损伤累积曲线Fig.10 Damage accumulation curves of the bridge element just below the dynamite under different blast height
图11是工况4~6下爆炸高度固定为1.0,m时,当TNT当量分别为800,kg、1,000,kg、1,200,kg时,炸药正下方桥梁单元的压力曲线.该曲线表明,相同爆炸高度的情况下,当TNT当量分别为800,kg、1,000,kg、1,200,kg时,单元所受的超压峰值的大小分别为245.10,MPa、278.43,MPa和407.84,MPa;TNT当量从800,kg增加到1,200,kg时,超压的峰值增加了66.40%.可见,TNT当量越大,爆炸冲击波对单元作用的超压峰值越大.以Tuler-Butcher损伤累积准则为依据,得到对该单元在不同炸药量下的损伤累积曲线,如图12所示.由图12可见,TNT当量越大,累积损伤因子越大,即损伤越严重.这些损伤累积曲线所反映出的各种规律可用于城市桥梁抗爆风险评估等后续模拟中.

图11 不同TNT当量时炸药正下方桥梁单元压力曲线Fig.11 Pressure curves of the bridge element just below the dynamite with different TNT equivalence blast loadings
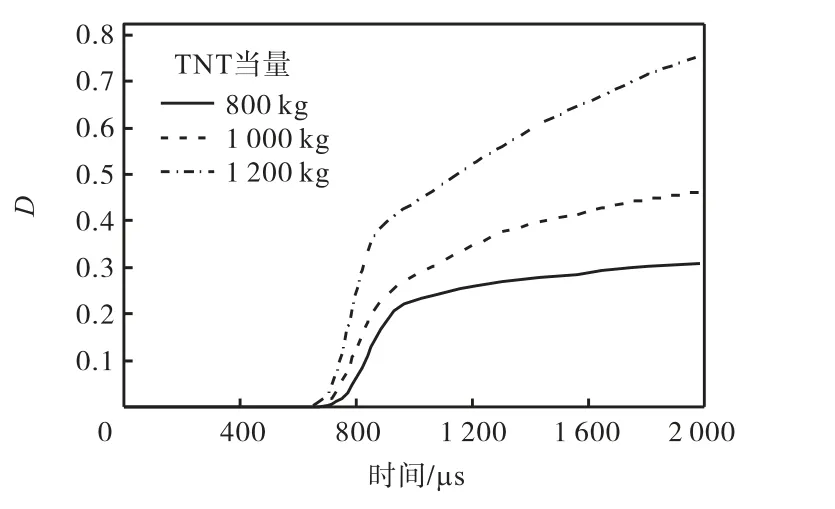
图12 不同TNT当量时炸药正下方桥梁单元的损伤累积曲线Fig.12 Damage accumulation curves of the bridge element just below the dynamite under different TNT equivalence blast loadings
5.3爆炸荷载作用下桥梁损伤过程的模拟
为了模拟桥梁在各个时间点上的损伤形态,在工况7和工况8中分别设置了TNT当量为10,000,kg的炸药.在模拟过程中发现,足量的炸药造成桥梁结构的严重破坏.图13和图14分别为工况7和工况8下桥梁在各时刻的Von-Mises应力分布.
从图13和图14中可以清楚地观察到桥梁从爆炸发生后到发生局部损伤的各阶段形态.在t=0.85,ms时刻,爆炸冲击波刚刚到达钢箱梁顶板,顶板上与炸药距离最近的局部区域内Von-Mises应力迅速增大;t=3.00,ms时刻,顶板上与炸药距离最近的桥梁单元开始失效,整座桥梁在爆炸冲击波的作用下发生了局部破坏;t=6.00,ms时刻,爆炸冲击波对桥梁产生的作用明显减弱,但桥梁整体结构在重力的作用下局部破坏范围进一步扩大;t=15.00,ms时刻,桥梁结构局部破坏的范围达到最大.数值模拟的结果可以为桥梁安全性评估和桥梁残余寿命的计算提供参考数据.

图13 工况7下各时刻桥梁的Von-Mises应力分布Fig.13 Von-Mises stress distribution of bridge at working condition 7

图14 工况8下各时刻桥梁的Von-Mises应力分布Fig.14 Von-Mises stress distribution of bridge at working condition 8
6 结 论
(1) 利用ANSYS/LS-DYNA软件进行建模时,分别采用SOLID164 8节点实体单元模拟空气和炸药,SHELL163 4节点薄壳单元模拟除吊杆外的全部桥梁结构,LINK160 3节点3D圆杆单元模拟吊杆.结果表明,计算模型能够很好地反映钢桁架拱桥结构在爆炸荷载作用下的动力及局部损伤特性.
(2) 爆炸荷载对桥梁的损伤呈现局部破坏特征,且损伤按4个阶段发展:第1阶段,爆炸冲击波传播到钢箱梁顶板,顶板上与炸药距离最近的局部区域内Von-Mises应力迅速增大;第2阶段,顶板上与炸药距离最近的桥梁单元开始失效,整座桥梁在爆炸冲击波的作用下会发生局部破坏;第3阶段,爆炸冲击波对桥梁产生的作用明显减弱,但桥梁整体结构在重力作用下的局部破坏范围进一步扩大;第4阶段,桥梁结构局部破坏的范围达到最大.
(3) 以Tuler-Butcher损伤累积准则为依据,对桥梁的损伤程度进行量化,所得到的损伤累积曲线表明,同等TNT当量的情况下,当爆炸高度分别为0.5,m、0.7,m和0.9,m时,炸药正下方桥梁单元在爆炸发生后的1.5,ms内,累积损伤因子分别为0.29、0.21和0.16;而在相同爆炸高度的情况下,当TNT当量分别为800,kg、1,000,kg、1,200,kg时,炸药正下方桥梁单元在爆炸发生后的2.0,ms内累积损伤因子分别为0.29、0.46和0.77,可见,近距离、大药量均可使桥梁局部损伤因子剧增.本文提出的分析方法和结果可为桥梁抗爆设计和爆炸风险评估提供参考.
参考文献:
[1] 刘建成,顾永宁. 桥墩塑性防撞装置的力学机理[J].上海交通大学学报,2003,37(7):990-994. Liu Jiancheng,Gu Yongning. Mechanism of plastic protection device for ship-bridge collision[J]. Journal of Shanghai Jiaotong University,2003,37(7):990-994(in Chinese).
[2] Winget D G,Marchand K A,Williamson E B. Analysis and design of critical bridges subjected to blast loads[J]. Journal of Structural Engineering,2005,131(8):1243-1255.
[3] Fujikura S,Michel B,Diego L. Experimental investigation of multihazard resistant bridge piers having concrete-filled steel tube under blast loading[J]. Journal of Bridge Engineering,2008,13(6):586-594.
[4] Gannon J C. Design of Bridges for Security Against Terrorist Attacks[D]. Austin:Cockrell School of Engineering,The University of Texas at Austin,2004.
[5] 邓荣兵,金先龙,陈向东,等. 爆炸冲击波作用下桥梁损伤效应的数值仿真[J]. 上海交通大学学报,2008,42(11):1927-1930. Deng Rongbing,Jin Xianlong,Chen Xiangdong,et al. Numerical simulation for bridge subjected the damage effect of to blast wave[J]. Journal of Shanghai Jiaotong University,2008,42(11):1927-1930(in Chinese).
[6] 张开金. 爆炸荷载作用下混凝土桥梁的损伤特性研究[D]. 西安:长安大学建筑工程学院,2009. Zhang Kaijin. Study on the Damage Mechanism of Concrete Bridge Under Blast Loading[D]. Xi’an:School of Civil Engineering,Chang’an University,2009(in Chinese).
[7] 蒋志刚,王 赟,严 波,等. 爆炸荷载作用下悬索桥竖弯响应的数值模拟[J]. 振动与冲击,2012,31(2):123-128. Jiang Zhigang,Wang Yun,Yan Bo,et al. Numerical simulation for vertical bending response of a suspension bridge under air explosion loading[J]. Journal of Vibration and Shock,2012,31(2):123-128(in Chinese).
[8] Tang E K C,Hao Hong. Numerical simulation of a cable-stayed bridge response to blast loads,PartⅠ:Model development and response calculations[J]. Engineer Structures,2010,32(10):3180-3192.
[9] Hao Hong,Tang E K C. Numerical simulation of a cable-stayed bridge response to blast loads,PartⅡ:Damage prediction and FRP strengthening[J]. Engineer Structures,2010,32(10):3193-3205.
[10] 孙三祥,高孟理,谢君泰,等. 易燃易爆物品运输车辆的分类与检测[J]. 公路与汽运,2006,22(5):26-28. Sun Sanxiang,Gao Mengli,Xie Juntai,et al. Classification and detection of flammable and explosive goods transport vehicles[J]. Highways & Automotive Applications,2006,22(5):26-28(in Chinese).
[11] 朱新明,蒋志刚. 钢箱梁爆炸冲击局部破坏数值模拟研究[D]. 长沙:国防科学技术大学指挥官基础教育学院,2011. Zhu Xinming,Jiang Zhigang. Numerical Simulation Investigation of Local Failure of Steel Box Girders Under Blast Loading[D]. Changsha:College of Basic Education for Commanding Officers,National University of Defense Technology,2011(in Chinese).
[12] 李裕春,时党用,赵 远. ANSYS11.0/LS-DYNA基础理论与工程实践[M]. 北京:中国水利水电出版社,2008. Li Yuchun,Shi Dangyong,Zhao Yuan. Basic Theory and Engineering Practice of ANSYS11.0/LS-DYNA[M]. Beijing:China Water and Power Press,2008(in Chinese).
[13] Benson D J. A mixture theory for contact in multi-material Eulerian formulations[J]. Computer Methods Applied Mechanics and Engineering,1997,140(1/2):59-86.
[14] Alia A,Souli M. High explosive simulation using multimaterial formulations[J]. Applied Thermal Engineering,2006,26(10):1032-1042.
[15] 白金泽. LS-DYNA 3D理论基础与实例分析[M]. 北京:科学出版社,2005. Bai Jinze. Basic Theory and Practice Analysis of LSDYNA 3D[M]. Beijing:Science Press,2005(in Chinese).
[16] Cheng M,Hung K,Chong O. Numerical study of water mitigation effects on blast wave[J]. Shock Waves,2005,14(3):217-223.
[17] 李建阳. 爆炸载荷下水中混凝土损伤破坏规律研究[D]. 合肥:中国科学技术大学工程科学学院,2010. Li Jianyang. Research on the Damage and Fracture Rules of Concrete in Water Due to Explosion Loading[D]. Hefei:School of Engineering Science,University of Science and Technology of China,2010(in Chinese).
[18] 卢红琴,刘伟庆. 空中爆炸冲击波的数值模拟研究[J]. 武汉理工大学学报,2009,31(19):105-108. Lu Hongqin,Liu Weiqing. Research on numerical simu lation of blast wave in air[J]. Journal of Wuhan University of Technology,2009,31(19):105-108(in Chinese).
[19] Tuler F R,Butcher B M. A criterion for the time dependence of dynamic fracture[J]. International Journal of Fracture,1968,4(4):431-437.
[20] 曹结东. 含损伤热粘塑性本构数值算法和铝锂合金动态响应研究[D]. 合肥:中国科学技术大学工程科学学院,2006. Cao Jiedong. Numerical Method for Thermo-Viscoplastic Damage Constitutive Relation and Research on Dynamic Response of Al-Li Alloys[D]. Hefei:School of Engineering Science,University of Science and Technology of China,2006(in Chinese).
[21] 蒋 东,李永池,郭 扬. Tuler-Butcher模型中考虑已有损伤影响的一种修正[J]. 高压物理学报,2009,23(4):271-276. Jiang Dong,Li Yongchi,Guo Yang. Modification of Tuler-Butcher model with damage influence[J]. Chinese Journal of High Pressure Physics,2009,23(4):271-276(in Chinese).
(责任编辑:樊素英)
Dynamic Response and Damage Process Analysis of Urban Bridge Subjected to Blast Load
Zhu Jinsong1, 2,Xing Yang1
(1. School of Civil Engineering,Tianjin University,Tianjin 300072,China;2. Key Laboratory of Coast Civil Structure Safety of Ministry of Education (Tianjin University),Tianjin 300072,China)
Abstract:In order to obtain reasonable anti-blast design and risk assessment of urban municipal bridges in a densely populated city,dynamic response and damage process analysis method for urban bridges subjected to blast load is proposed in this paper. By analyzing the explosion risk sources of urban bridges,the explosion source types and blast load conditions likely to be encountered by urban bridges are determined. Then,the finite element models of bridge,dynamite and air are established in ANSYS/LS-DYNA software. The dynamite model and the air model are defined by the JWL (Jones-Wilkins-Lee) state equation and linear polynomial state equation,respectively. The ALE (arbitrary Lagrange-Euler) algorithm is used to simulate the propagation of shock wave actuated by explosion. The effects of position and quantity of dynamite on the response of displacement and the Von-Mises stress distribution in the key parts of the bridge are investigated,and then the damage process and failure modes of the bridge are analyzed. Based on the Tuler-Butcher cumulative damage rule,the damage accumulation curves under different explosion distances and TNT equivalence blast loadings of specified elements are obtained. In the end,taking a large-span steel truss arch bridge as an illustrative example,the calculation process of the proposed method in this paper is described. The results of this paper can be used as the foundation for anti-blast design and risk assessment of bridge.
Keywords:blast load;ALE algorithm;steel truss arch bridge;dynamic response;numerical simulation
通讯作者:朱劲松,jszhu@tju.edu.cn.
作者简介:朱劲松(1975— ),男,博士,教授.
基金项目:天津市科技支撑计划重点项目(11ZCKFSF00300);国家自然科学基金资助项目(51178305).
收稿日期:2013-07-25;修回日期:2013-10-22.
DOI:10.11784/tdxbz201307078
中图分类号:TU997
文献标志码:A
文章编号:0493-2137(2015)06-0510-10
