模糊自抗扰控制器在挠性航天器振动抑制中的应用

刘福才， 陈 鑫， 贾亚飞， 刘彩凤

(燕山大学 工业计算机控制工程河北省重点实验室，秦皇岛 066004)

模糊自抗扰控制器在挠性航天器振动抑制中的应用

刘福才， 陈 鑫， 贾亚飞， 刘彩凤

(燕山大学 工业计算机控制工程河北省重点实验室，秦皇岛 066004)

针对挠性航天器在轨运动过程中挠性结构的持续振动问题，提出一种基于模糊控制原理的改进型自抗扰控制方法，实现对挠性航天器的振动抑制。通过非线性自抗扰控制器快速地抑制挠性航天器的低频振动，并结合模糊控制实现自抗扰控制器(Auto Disturbance Rejection Controller, ADRC)参数的自整定，提高自抗扰控制器的性能。将仿真结果与PD控制和非线性自抗扰控制进行对比，结果表明该控制算法能更加快速有效地抑制挠性航天器的振动，具有重要的理论研究和工程应用价值。

自抗扰控制器；模糊控制；振动抑制；挠性航天器

随着科学技术的不断发展，航天器的规模越来越大，结构也越来越复杂。由于降低结构质量仍是结构设计追求的一项重要指标，因而具有大挠性成为很多航天结构的一个特点。挠性航天器在轨运动过程中，其中心刚体和挠性附件之间存在强烈的耦合，会导致挠性结构的持续振动，进而影响航天器的运动和控制，因此，国内外学者[1-3]对挠性航天器的振动抑制问题进行了大量研究。

目前，挠性航天器的控制技术主要包括被动控制技术、主动控制技术和主被动一体化振动控制技术[1]。针对挠性航天器的振动问题，文献[4]采用带有非线性阻尼的全系数自适应方法，该方法在黄金分割自适应控制方法的基础上，通过引入振动能量阻尼项得到了比较理想的振动抑制效果；文献[5]提出了一种直接自适应分层模糊广义预测控制方法，避免了模糊控制器中的规则数目随系统变量个数呈指数增长问题，能快速地抑制挠性航天器的低频振动；文献[6]基于Timoshenko梁理论，采用滑模变结构控制方法，对使用开关喷气推力调姿的航天器动力学与控制问题进行了研究；文献[7]采用分力合成与正位置反馈相结合的控制方法来抑制振动；文献[8]提出一种基于自适应鲁棒方法和H∞相结合的控制方案；文献[9]采用的是被动控制策略，通过使用分流压电传感器避免了主动控制策略不稳定的缺点；文献[10]基于逆动力学设计了两个控制器来控制航天器的姿态，并通过假定在中心刚体的三个方向上有三个力矩来解决非最小相位特性对设计的阻碍；文献[11]考虑了挠性附件模态难以测得以及存在外界干扰力矩等问题，提出了一种基于输入成形和反馈控制联合的主动控制策略；文献[12]用频带分离的方法将姿态控制与挠性振动控制解耦，并设计了积分型姿态控制器和正位置反馈振动控制器。

但是，以往的控制器设计方法算法复杂且超调量大，并且一些线性控制方案不能解决振动快速抑制和稳态精度的矛盾问题。因此，本文采用模糊自抗扰控制器，在非线性自抗扰控制器的基础上结合模糊算法，避免了线性控制方案的缺点，并利用了自抗扰控制器不依赖于被控对象精确的数学模型[13]和超调小、响应速度快、精度高、抗扰能力强及算法简单，被调参数物理意义明确等优点，同时采用模糊控制对自抗扰控制器中的误差反馈环节的参数进行整定，使自抗扰控制系统有更好的鲁棒性能和更好的适应性。仿真结果表明该控制器能快速有效地抑制挠性航天器的振动，具有重要的理论研究和工程应用价值。

1 航天器的数学模型

本文主要研究挠性航天器振动抑制问题，使用单轴动力学模型进行分析可使问题更清楚，表达更方便。挠性航天器的单轴转动动力学模型如下：

(1)

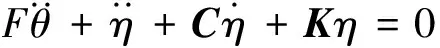
(2)

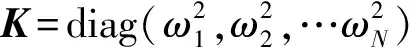
2 模糊自抗扰控制器设计

自抗扰控制理论是一种利用简单非线性部件对非线性系统的状态量及其所受干扰进行检测，进而利用非线性误差反馈规律进行总体补偿的非线性控制策略。ADRC具有很强的抗干扰能力，不依赖被控对象精确的数学模型，并且能够获得较强的鲁棒性[11]。其控制结构由跟踪微分器(Tracking differentiator, TD)，扩张状态观测器(Extended State Observer, ESO)和非线性状态误差反馈(Nonlinear State Error Feedback, NLSEF)组成。

2.1 非线性自抗扰控制器

非线性ADRC是一种新型的反馈非线性化控制策略，它通过使用扩张状态观测器(ESO)实时、迅速、准确地获得对象摄动及外扰作用的信息，再通过自抗扰控制器的补偿作用就可实现对象的反馈非线性化和反馈确定性化。以下分两种情形对挠性航天器模型进行讨论。

情形1：无外界扰动

由动力学方程(1)和(2)可得：

(3)

其中:

自抗扰控制器不依赖被控对象精确的数学模型，可以将耦合看作扰动并进行实时补偿[14]，所以可把上述状态方程中不可测量的模态及其速率的组合项d0(t)看成是由挠性附件引起的干扰。

情形2：有外界扰动

有外界扰动时，式(1)和式(2)变为：

(4)

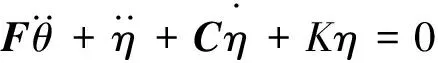
(5)

式中:T为作用在挠性航天器本体上的外干扰力矩。

式(4)和式(5)可写成如下状态方程的形式：

(6)

其中:

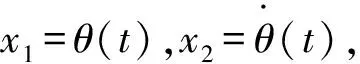
(7)

其中:b=(J-FTF)-1，d(x1,x2,T,t)为总和扰动。

虽然总和扰动d(x1,x2,T,t)在上述两种情形中具体表达式不同，但是ESO不依赖对象的精确数学模型，并可以扩张出一个新的状态量对控制系统中的不确定性(系统未建模部分以及内外扰动之和)进行估计，因此只要合理选择ESO的参数，就可以获得不同情况下对应扰动的观测量。

由式(7)可以看出应采用二阶自抗扰控制器，相应采用三阶的ESO结构。图1给出了二阶自抗扰控制器的结构图。

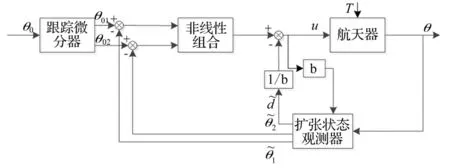
图1 二阶非线性自抗扰控制器结构图Fig.1 Structure diagram of thesecond-order nonlinear ADRC controller

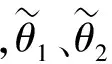
本文所使用的二阶微分跟踪器可以根据参考输入及被控对象的限制来安排过渡过程，避免控制量剧烈变化，其公式为：

(8)

式中:r为可调参数。

(9)

其中:β01>0，β02>0，β03>0为扩张状态观测器的增益，并且影响ESO的跟踪效果，fal为如下非线性函数：

(10)

其中:α为非线性因子，δ为线性段的区间长度，e为偏差。

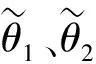
(11)

式中:β1>0、β2>0为误差反馈增益。

式(8)、式(9)和式(11)构成了自抗扰控制器的控制算法，通过合理调整各部分参数可以使θ→θ0，从而实现在调整姿态的同时抑制振动。

2.2 稳定性分析

定理1 对于系统(7)，合理选择扩张状态观测器的参数，可以保证其稳定性。

证: 定义系统(9)和系统(7)的误差方程为：

(12)

可将上述方程进一步写为：

(13)

当该误差系统进入稳态时，有：

(14)

结合式(5)和式(6)，当δ=0时误差系统的稳态误差为：

(15)

2.3 模糊自抗扰控制器

非线性ADRC中TD参数基本上可以固定化，ESO可以根据ESO参数与扰动幅值成正比的关系来确定，而NLSEF部分由于非线性的存在使其参数整定有很大难度，因此本文采用模糊控制对NLSEF中的参数β1,β2进行修改，从而实现系统变化情况下增益β1,β2的自整定。

通常模糊控制器由四部分组成：模糊化接口，将精确的输入、输出值转换为模糊的语言值；规则库，它是由若干条控制规则组成，这些控制规则根据人类控制专家的经验总结得出；模糊推理，根据模糊输入和规则库中蕴涵的输入输出关系，通过模糊推理方法得到模糊控制器的输出模糊值；清晰化接口，将模糊推理得到的模糊输出值是输出论域上的模糊子集，转化为精确控制律。

模糊自抗扰控制器控制框图如图2所示。

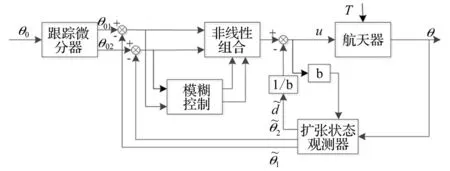
图2 模糊自抗扰控制器框图Fig.2 Structure diagram of the fuzzy ADRC controller

选择输入语言变量为误差e和误差变化率de/dt，语言变量值取{NB，NM，NS，ZE，PS，PM，PB}七个模糊值；选择输出语言变量为β1,β2，语言变量值也取{NB，NM，NS，ZE，PS，PM，PB}七个模糊值。隶属度函数均采用灵敏度较高的三角形函数，输入e和de/dt的隶属度均选为[-6,6]，输出β1,β2的隶属度均选为[-6,6]。本文采用的模糊控制规则如表1、表2所示。

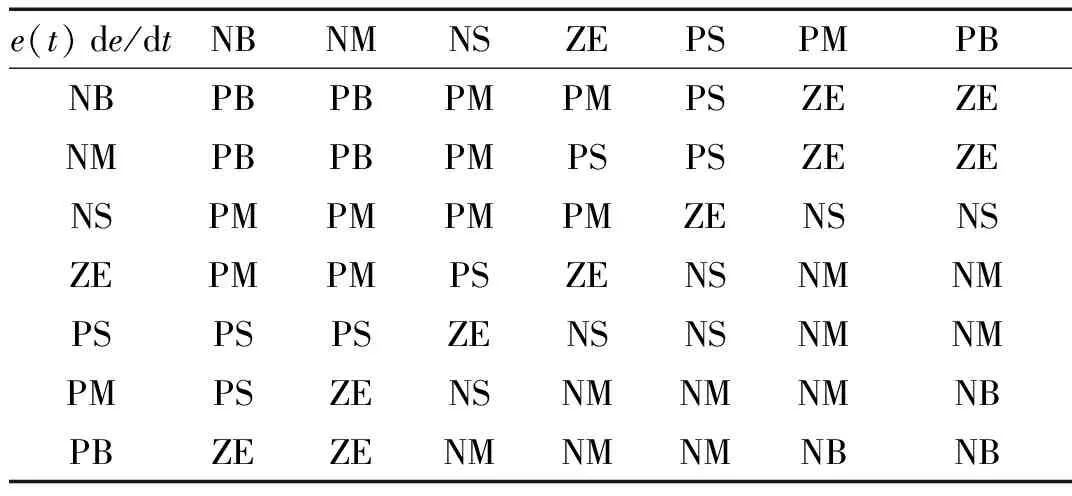
表1 β1的模糊逻辑

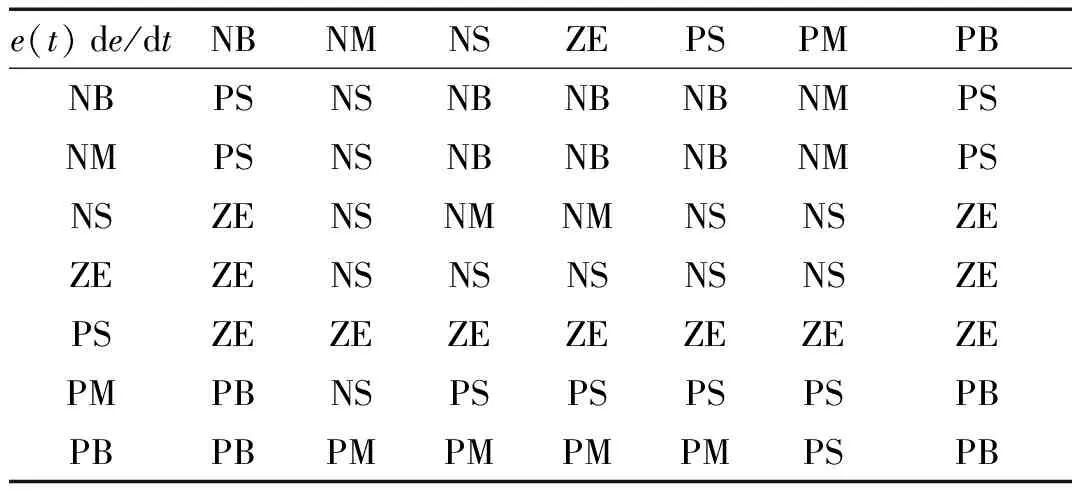
表2 β2的模糊逻辑

根据模糊规则表，可以用fuzzy( )函数可视地建立起整个模糊推理系统，该系统有两路输入和三路输出。

3 仿真研究

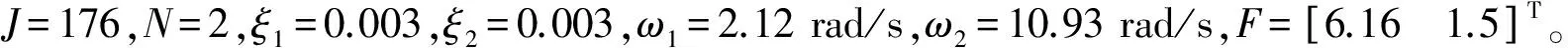
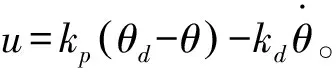
3.1 无外界扰动

由于无外界扰动是一种理想情况，因此本文只对比了三种控制系统在无外界扰动时的姿态角响应曲线。仿真结果如图3～图5所示。

从图3～图5可以看出，与PD控制方法相比，非线性自抗扰控制器能够快速地抑制航天器的振动，而模糊自抗扰控制器能够比非线性自抗扰控制器更好地使系统收敛，控制效果更好。

3.2 有外界扰动

由于航天器在太空中仍不可避免地受到外界环境的干扰，因此本文着重考虑有外界扰动时的情形，对三种控制系统的姿态响应情况及模态振动情况都进行了仿真分析。仿真结果如图6～图17所示。

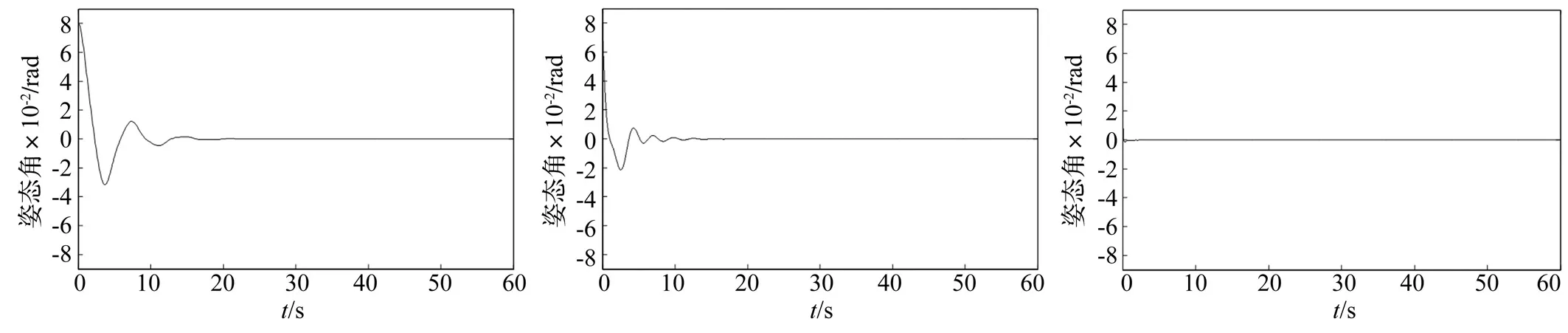
图3 PD控制下的姿态角响应曲线Fig．3TimeresponseofattitudeangleusingPDcontroller图4 非线性ADRC控制下的姿态角响应曲线Fig．4TimeresponseofattitudeangleusingnonlinearADRCcontroller 图5 模糊自抗扰控制下的姿态响应曲线Fig．5TimeresponseofattitudeangleusingfuzzyADRCcontroller

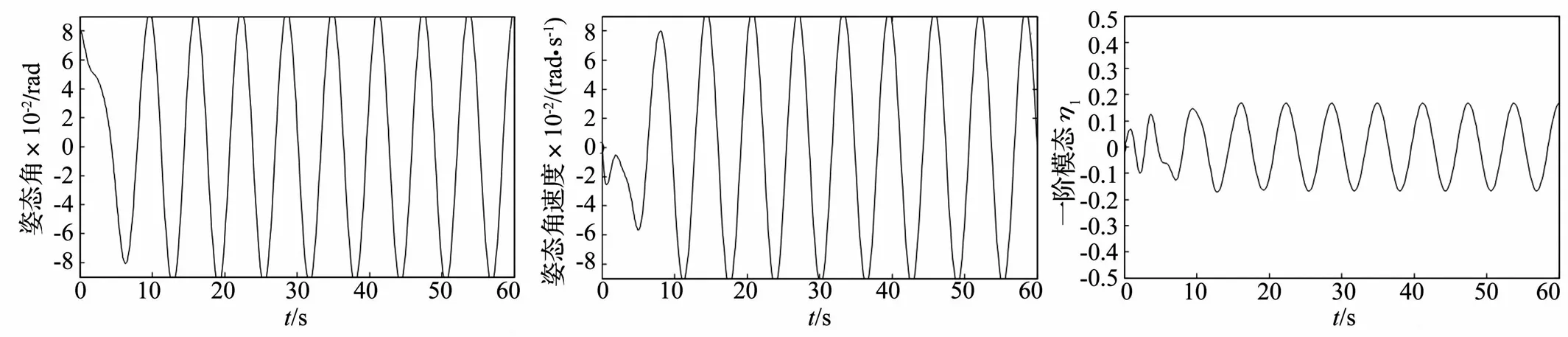
图6 PD控制下的姿态角响应曲线Fig．6TimeresponseofattitudeangleusingPDcontroller图7 PD控制下的姿态角速度响应曲线Fig．7TimeresponseofattitudeanglevelocityusingPDcontroller图8 PD控制下的一阶模态振动曲线Fig．8TimeresponseofthefirstordervibrationmodeusingPDcontroller

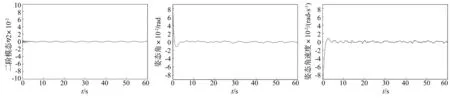
图9 PD控制下的二阶模态振动曲线Fig．9TimeresponseofthesecondordervibrationmodeusingPDcontroller图10 非线性ADRC控制下的姿态角响应曲线Fig．10TimeresponseofattitudeangleusingnonlinearADRCcontroller图11 非线性ADRC控制下的姿态角速度响应曲线Fig．11TimeresponseofattitudeanglevelocityusingnonlinearADRCcontroller

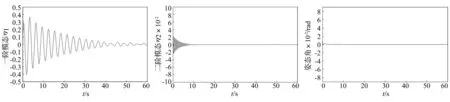
图12 非线性ADRC控制下的一阶模态振动曲线曲线Fig．12TimeresponseofthefirstordervibrationmodeusingnonlinearADRCcontroller图13 非线性ADRC控制下的二阶模态振动曲线曲线Fig．13TimeresponseofthesecondordervibrationmodeusingnonlinearADRCcontroller图14 模糊自抗扰控制下的姿态角响应曲线Fig．14TimeresponseofattitudeangleusingfuzzyADRCcontroller

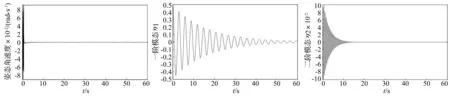
图15 模糊自抗扰控制下的姿态角速度响应曲线Fig．15TimeresponseofattitudeanglevelocityusingfuzzyADRCcontroller图16 模糊自抗扰控制下的一阶模态振动曲线Fig．16TimeresponseofthefirstordervibrationmodeusingfuzzyADRCcontroller图17 模糊自抗扰控制下的二阶模态振动曲线Fig．17TimeresponseofthesecondordervibrationmodeusingfuzzyADRCcontroller

从图6～图17可以看出，PD控制系统在有外界干扰时无法达到期望的姿态角度，非线性自抗扰控制系统在60 s时也仍存在挠性振动，而本文设计的模糊自抗扰控制系统在完成姿态机动控制任务的同时，也很好地抑制了挠性附件的振动。

4 结 论

针对挠性航天器在轨运动中的振动问题，设计了模糊自抗扰控制器。该控制器结合了自抗扰控制器和模糊控制的优点，利用自抗扰控制器对航天器的内外扰动进行实时补偿，抑制挠性航天器的振动，并采用模糊控制实现参数β1和β2在变化情况下的自整定。仿真结果表明了所设计的控制器能快速有效地抑制挠性航天器的振动，具有重要的理论研究和工程应用价值。

[1] 刘天雄, 林益明, 王明宇,等. 航天器振动控制技术进展[J].宇航学报, 2008, 29(1): 1-11. LIU Tian-xiong, LIN Yi-ming, WANG Ming-yu,et al. Review of the spacecraft vibration control technology[J]. Journal of Astronautics, 2008, 29(1): 1-11.

[2] Song Gang-bing, Agrawal B N. Vibration suppression of flexible spacecraft during attitude control[J]. Acta As-ronautica, 2001, 49(2): 73-83.

[3] Kong Xian-ren, Yang Zheng-xian. Combined feedback control and input shaping for vibration suppression of flexible spa-cecraft[C]. Proceedings of the 2009 IEEE International Conf-erence on Mechatronics and Automation. Changchun: IEEE, 2009:3257-3262.

[4] 王晓磊, 吴宏鑫. 挠性航天器振动抑制的自适应方法及实验研究[J]. 宇航学报, 2005, 26(3): 275-291. WANG Xiao- lei, WU Hong-xin. Adaptive control scheme and experiment for vibration suppression of flexible spacecraft[J]. Journal of Astronautics, 2005, 26(3): 275-291.

[5] 孙多青. 分层模糊广义预测控制及其在挠性航天器振动抑制中的应用[J]. 宇航学报, 2009, 30(4): 1537-1543. SUN Duo-qing. Hierarchical fuzzy generalized predictive control and its application in vibration suppression of flexible spacecraft[J]. Journal of Astronautics, 2009, 30(4):1537-1543.

[6] 陈涛, 胡超, 黄文虎. 航天器姿态调整时的变结构控制与振动抑制方法[J]. 宇航学报, 2007, 28(5): 1199-1204. CHEN Tao, HU Chao, HUANG Wen-hu. Variable structure control and vibration suppression of spacecraft during attitude maneuver[J]. Journal of Astronautics, 2007, 28(5): 1199-1204.

[7] Hu Q L, Ma G F.Vibration suppression offlexible spacecraft during attitude maneuvers[J].J of Guidance, Control and Dynamics, 2005, 28(2): 377-380.

[8] 袁国平, 史小平, 李隆. 航天器姿态机动的自适应鲁棒控制方法及主动振动抑制[J]. 振动与冲击, 2013, 32(12): 110-115. YUAN Guo-ping, SHI Xiao-ping, LI Long. Adaptive robust attitude maneuver control of a flexible spacecraft with active vibration suppression[J]. Journal of Vibration and Shock, 2013, 32(12): 110-115.

[9] Sales T P, Rade D A, Souza L C G. Passive vibration control of flexible spacecraft using shunted piezoelectric transducers[J]. Aerospace Science and Technology, 2013 (29): 403-412.

[10] Malekzadeh M, Naghash A, Talebi H A. Slewing and vibration control of a nonlinear flexible spacecraft[C]. American Control Conference, USA, 2010.

[11] 孔宪仁, 杨正贤, 叶东,等. 基于输入成形的柔性航天器振动闭环抑制方法研究[J]. 振动与冲击, 2010, 29(3): 72-76. KONG Xian-ren, YANG Zheng-xian, YE Dong, et al.Feedback control in conjunction with input shaping for flexible spacecraft vibration suppression[J]. Journal of Vibration and Shock, 2010, 29(3): 72-76.

[12] 李洋, 仇原鹰, 张军,等. 一种挠性航天器的自适应姿态控制与振动控制[J]. 振动与冲击, 2009, 28 (12): 178-182. LI Yang, QIU Yuan-ying, ZHANG Jun,et al. Adaptive attitude control and active vibration control of the flexible spacecraft[J]. Journal of Vibration and Shock, 2009, 28(12): 178-182.

[13] 康莹, 李东海, 老大中. 航天器姿态的自抗扰控制与滑模控制的性能比较[J]. 控制理论与应用, 2013, 30(12): 1623-1629. KANG Ying, LI Dong-hai, LAO Da-zhong. Performance comparison of active disturbance rejection control and sliding mode control in spacecraft attitude control[J]. Control Theory and Applications, 2013, 30(12): 1623-1629.

[14] ZHENG Q, CHEN Z Z, GAO Z Q. A practical approach to disturbance decoupling control[J]. Engineering Practice, 2009, 17(9): 1016-1025.

Application of fuzzy auto disturbance rejection controller in flexible spacecraft vibration suppression

LIU Fu-cai, CHEN Xin, JIA Ya-fei, LIU Cai-feng

(Key Lab of Industrial Computer Control Engineering of Hebei Province, Yanshan University, Qinhuangdao 066004, China)

Considering the lasting vibration of flexible structure in the on-orbit motion process of flexible spacecraft, an auto disturbance rejection control(ADRC) strategy based on fuzzy control theory was proposed, so as to realize the vibration suppression of the flexible spacecraft. The nonlinear auto disturbance rejection controller was designed to quickly suppress the low frequency vibration in the flexible spacecraft. In order to improve the performance of ADRC, fuzzy control was also adopted to adjust the ADRC parameters easily. The simulation results of the PID control and the nonlinear ADRC control were compared and it is concluded that the controller can suppress the vibration of flexible spacecraft more quickly and efficiently. The results are of important value for further theoretical research and other engineering applications.

auto disturbance rejection controller; fuzzy control; vibration suppression; flexible spacecraft

国家高技术研究发展计划(863计划)资助课题;河北省自然科学基金资助课题(F2015203362)

2014-01-08 修改稿收到日期：2014-04-30

刘福才 男，博士，教授，1966年生

TP241

A

10.13465/j.cnki.jvs.2015.09.002