基于Hybrid EnSRF-En3DVar的雷达资料同化研究

闵锦忠,刘盛玉,2,毕坤,杜宁珠

(1.气象灾害教育部重点实验室(南京信息工程大学),江苏 南京 210044;2.94833部队,江西 南昌 330201;3.94608部队,江苏 南京 210022)



基于Hybrid EnSRF-En3DVar的雷达资料同化研究

闵锦忠1,刘盛玉1,2,毕坤3,杜宁珠1

(1.气象灾害教育部重点实验室(南京信息工程大学),江苏 南京 210044;2.94833部队,江西 南昌 330201;3.94608部队,江苏 南京 210022)

基于WRF模式构建了Hybrid EnSRF-En3DVar同化系统,该系统使用EnSRF方案直接更新集合扰动。利用构建的同化系统针对台风“桑美”分别进行集合协方差权重敏感性试验和同化雷达不同观测资料的敏感性试验。集合协方差权重敏感性试验发现:当集合协方差权重分别为0.25、0.5和0.75时,同化效果优于3DVar试验,其中0.75的集合协方差权重试验得到了分析场的最优估计;当集合协方差权重为1.0时,分析场最差。同化雷达不同观测资料的敏感性试验表明,联合同化雷达径向风及反射率能有效改善大气湿度场和风场,但对风场的改善效果不如仅同化雷达径向风好。将EnSRF集合扰动更新方案与扰动观测方案综合分析发现,扰动观测方案集合离散度较小,计算代价大,EnSRF方案优于扰动观测方案。

资料同化;Hybrid EnSRF-En3DVar;多普勒雷达;台风

0 引言

在我国,台风引发的灾害居各种自然灾害之首,对台风的预测、预警是气象领域的研究热点。就目前大气探测水平而言,对台风系统温度场、湿度场和风场的监测依然是探测工作的难点,初始资料缺陷制约了数值模式对台风系统的预报准确性。多普勒雷达由于其高时空分辨率有助于模式改善近海台风的初始场精度。近年来,国内外有不少针对多普勒雷达资料的同化工作,研究证明利用雷达资料能较好地改进模式大气初始场结构(王顺凤等,2011;陈杰等,2012;耿建军等,2012;Li et al.,2012;Gao and Stensrud,2014)。

三维变分资料同化(three dimensional variational,3DVar)能够较容易地利用质量连续方程和其他适当的模式方程作为弱约束条件,在台风等对流尺度天气过程同化中应用广泛。但3DVar使用的背景误差协方差静态且各项均匀同性。四维变分同化(four dimensional variational,4DVar)尽管在分析中可隐式调整背景误差协方差,具备“流依赖”的特性,但4DVar必须依赖的伴随模式过于复杂且并非所有物理过程都可反向积分。同样是四维同化方案,集合卡尔曼滤波(Ensemble Kalman Filter,EnKF)方法在分析循环中可利用集合预报结果动态调整背景误差,但存在小样本引起的不满秩和采样误差(Gao and Stensrud,2014)。

目前,针对变分和EnKF的优缺点已被广泛讨论,为了尽量吸收二者优点,不少学者建议使用集合和变分混合(Hybrid)的同化方法(Hamill and Snyder,2000;Lorenc,2003)。此后,关于Hybrid同化的研究工作广泛开展,Hybrid同化在数值预报模式中得以实现(Wang et al.,2008a,2008b;陈耀登等,2014)并在对流尺度天气系统中得到深入研究(Li et al.,2012)。研究表明Hybrid同化方法潜力巨大,可兼顾3DVar和EnKF的优势。

Lorenc(2003)通过扩展控制变量法将集合背景误差协方差增加到三维变分目标函数中的方法也称为集合—三维变分混合同化(Hybrid Ensemble and 3DVar,En3DVar)。但该方法在后续预报中不能像EnKF一样自然更新集合成员,必须采取辅助的扰动更新方案。目前,针对En3DVar的扰动更新方案主要有以下两种:1)集合变换卡尔曼滤波(Ensemble Transform Kalman Filter,ETKF;Wang et al.,2008a,2008b),该方案利用常规观测通过ETKF全场更新每个集合成员,由于雷达资料具有较高的时空分辨率,全场更新计算代价巨大;同时由于该方案未引入局地化,更新过程中易引入虚假相关。2)扰动观测方案(Perturbed Observation method,PO;Li et al.,2012),该方案与早期EnKF研究使用的扰动观测法类似,即在原始观测基础上叠加满足Gauss分布的随机扰动,之后利用3DVar或Hybrid方法更新每一个集合成员。该方案可避开ETKF方案的不足,但会引入额外的采样误差;从实际执行效果看,该方案集合离散度较小,且需分别更新集合成员导致计算代价较大。

Dowell et al.(2004)指出,在多普勒雷达的高反射率区域叠加一定噪音,可一定程度上改善EnKF同化雷达资料的效果。高反射率区域代表着对流发展最旺盛的区域,其各种要素的变化具有高度的不确定性。本研究利用这一特点,针对上述两种方案的优缺点,构造了一种基于集合均方根滤波(Ensemble Squared Root Filter,EnSRF)的集合扰动更新方案。该方案可不需事先对观测进行扰动,避免引入虚假误差;而选取高反射率位置作为扰动更新区域,有效抑制了虚假回波的发生;同时EnSRF可方便的引入局地化和协方差膨胀等抑制滤波发散的方案。利用该方案结合En3DVar形成一种新的同化系统,称之为Hybrid EnSRF-En3DVar。

1 Hybrid EnSRF-En3DVar同化系统简介

在En3DVar同化中,“流依赖”的集合协方差信息通过扩展控制变量法引入到变分目标函数,En3DVar的理论基础及具体公式推导见Lorenc(2003)及Wang et al.(2008a)。

Whitaker and Hamill(2002)为避免传统EnKF扰动观测带来的采样误差,提出了一种基于EnSRF的确定性方法。由于该算法中平均场和扰动场具有线性叠加关系,且扰动场各变量具备物理关联性,可直接描述模式大气的不确定性。本研究将EnSRF计算的扰动场与En3DVar更新的分析场进行叠加,更新所有集合成员。EnSRF更新集合扰动场算法形式如下,公式具体含义和解释见Whitaker and Hamill(2002):

(1)

K=PbHT(HPbHT+R)-1,

(2)

(3)

图1给出了HybridEnSRF-En3DVar循环同化的基本流程框架,假设初始时刻有k个集合成员的背景预报场,每次循环同化具体执行流程如下:1)在分析时刻,通过En3DVar方法得到分析场;2)读取雷达资料,选取一定阈值反射率的观测位置,利用EnSRF方案仅更新集合扰动场;3)将更新后的扰动场叠加到分析场上,形成一组新的集合成员。

图1 Hybrid EnSRF-En3DVar系统流程图Fig.1 Flowchart of Hybrid EnSRF-En3DVar system

2 试验设计

2.1 真实场构造与模拟雷达观测制作

研究基于WRFV3.3.1,选取2006年台风“桑美”作为研究个例,利用模式计算的模拟雷达资料检验Hybrid EnSRF-En3DVar同化系统。模拟区域中心122.55°E、25.47°N,试验采取30 km(120 s)/10 km(40 s)、垂直28层的两重双向嵌套方案,积云对流参数化方案为Kain-Fritcsh,微物理方案使用WSM6,行星边界层方案为YSU。图2给出了WRF模拟区域和雷达探测范围。

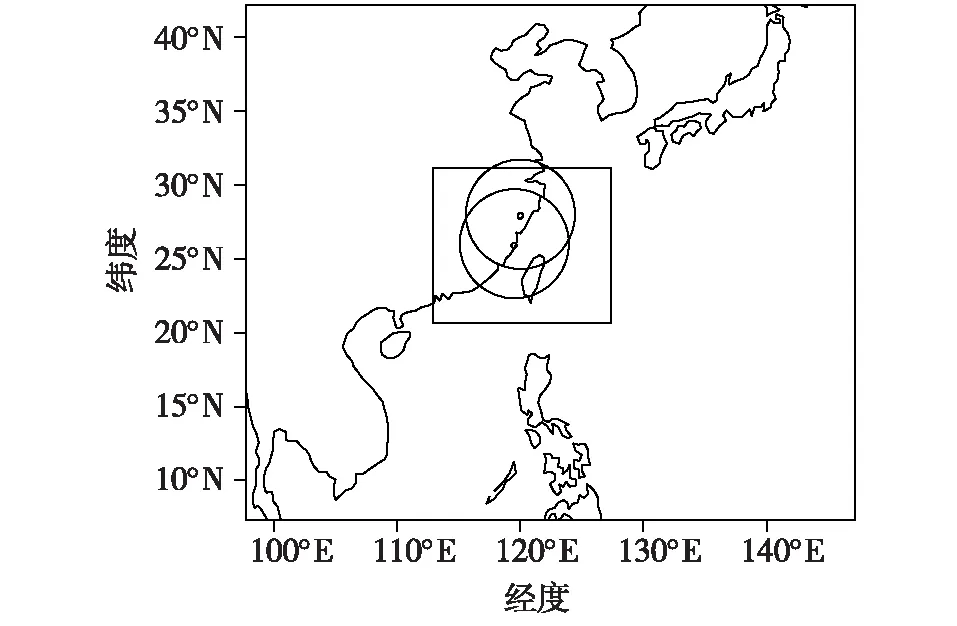
图2 模拟采用的两重嵌套区域示意图(圆圈:雷达扫描范围)Fig.2 Schematic diagram of two-fold nesting region for numerical simulation(circles:scanning range of radar)

由于模式和初始资料缺陷,目前模式中描述的台风往往强度偏弱。本研究利用Bogus方法(Zou and Xiao,2000)初始化台风,强迫台风系统快速发展。台风中心初始位置128.5°E、23.9°N,最大风速半径处风速40 m/s,最大风圈半径70 km,最大风速比0.8。选定2006年8月9日00时(世界时,下同)作为初始积分时刻,向后积分27 h制作“真实场”。

模拟雷达资料根据“真实场”计算并叠加具有Gauss分布的随机误差,反射率和径向速度的标准差分别为5 dBz和2 m/s。选取福州和厦门两部雷达,设置扫描半径为径向风460 km、反射率为460 km,取扫描范围内所有模式格点数据作为模拟雷达资料。从10日00时开始,间隔30 min制作一次模拟雷达资料,直至10日03时。雷达观测算子参考Sun and Crook(1997)。

2.2 试验设置

3DVar试验,背景误差协方差矩阵采用NMC方法(Parrish and Derber,1992)生成,由于NMC方法生成的背景误差协方差主要反应大尺度误差结构特征,直接运用到风暴尺度的雷达资料同化中欠妥(Liu et al.,2005),所以本研究将静态背景误差协方差的水平相关尺度减小到0.3(Li et al.,2012)。在9日00时做24 h单一的确定性spin-up,从10日00时开始每30 min同化一次模拟雷达观测数据。

Hybrid试验,静态背景误差协方差设置同3DVar试验,集合协方差权重给予了不同设置;同化的背景场是集合预报的平均场,扰动更新采用EnSRF方案或PO方案,同化和更新的位置都选择10 dBz以上区域,水平响应半径相同。在9日00时进行21 h单一的确定性spin-up,利用RandomCV方法在9日21时构造30个集合成员(扰动的标准偏差对水平风场是2 m/s,温度是0.6 K,气压是0.3 hPa,水汽混合比是0.9 g/kg),并进行3 h集合spin-up,同化过程中EnSRF方案设置松弛膨胀系数0.5(Zhang et al.,2004)、水平局地化半径60 km(Li et al.,2012)、垂直局地化半径10 km(Zhang et al.,2004),PO方案设置扰动大小同模拟雷达,完整同化流程同3DVar试验。各试验具体过程和设置见表1和图3。

表1 试验名称及设计方案

Table 1 Names of experiments and their design schemes

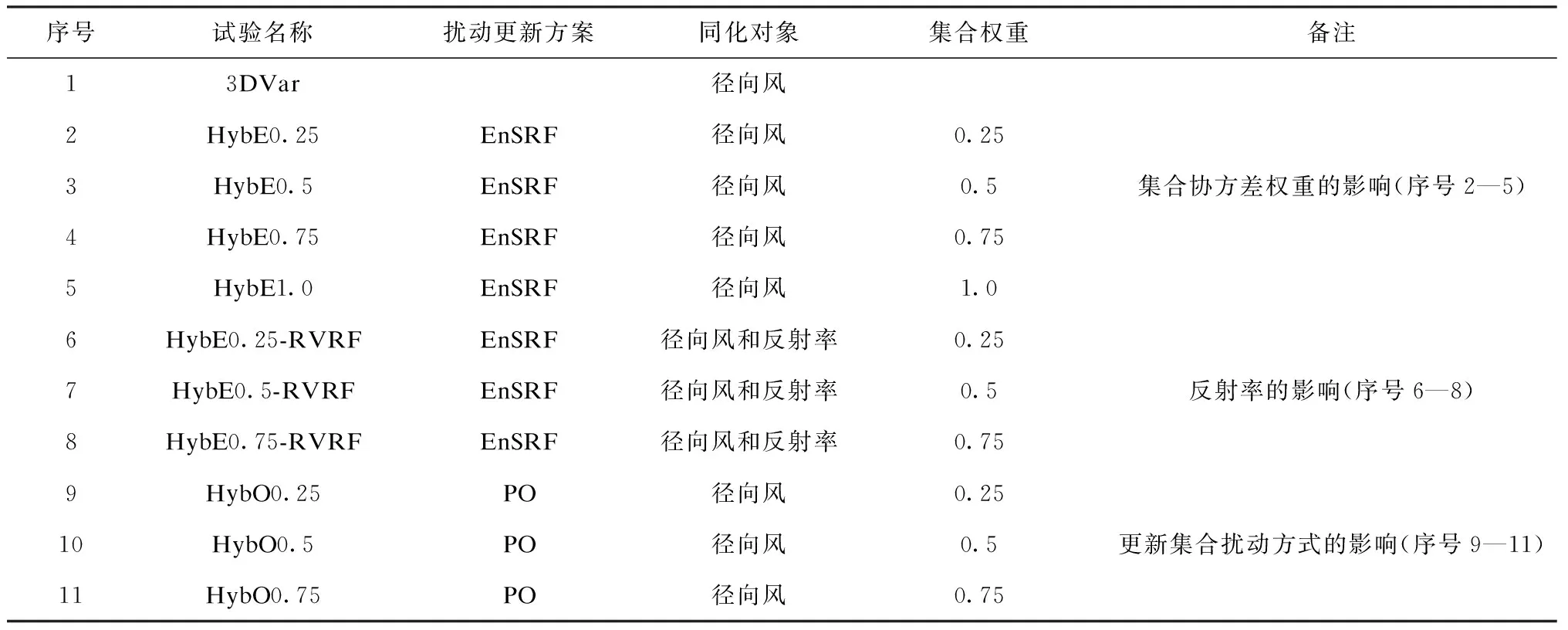
序号试验名称扰动更新方案同化对象集合权重备注13DVar径向风2HybE0.25EnSRF径向风0.253HybE0.5EnSRF径向风0.5集合协方差权重的影响(序号2—5)4HybE0.75EnSRF径向风0.755HybE1.0EnSRF径向风1.06HybE0.25-RVRFEnSRF径向风和反射率0.257HybE0.5-RVRFEnSRF径向风和反射率0.5反射率的影响(序号6—8)8HybE0.75-RVRFEnSRF径向风和反射率0.759HybO0.25PO径向风0.2510HybO0.5PO径向风0.5更新集合扰动方式的影响(序号9—11)11HybO0.75PO径向风0.75

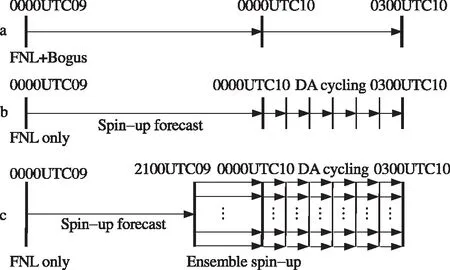
图3 试验流程图 a.Nature;b.3DVar;c.HybridFig.3 Flowchart of experiments a.Nature;b.3DVar;c.Hybrid

3 试验结果分析

3.1 集合协方差权重的影响

目前,关于集合协方差和静态协方差的最优权重尚在研究阶段,现有研究认为集合协方差权重为0.5、0.75或1.0时可以达到更好效果(Wang et al.,2008a)。为了验证集合协方差权重系数对Hybrid EnSRF-En3DVar同化系统的影响,设置Hybrid试验同化台风“桑美”的模拟雷达径向风,集合权重系数分别设置为0.25、0.5、0.75及1.0,并与3DVar试验进行对比。

图4 2006年8月10日03时近地面风矢量(箭矢;单位:m/s)和组合反射率(阴影区;单位:dBz) a.Nature;b.3DVar;c.HybE0.25;d.HybE0.5;e.HybE0.75;f.HybE1.0Fig.4 Near surface wind vectors(arrows;units:m/s) and composite reflectivities(shadings;units:dBz) at 0300 UTC 10 August 2006 a.Nature;b.3DVar;c.HybE0.25;d.HybE0.5;e.HybE0.75;f.HybE1.0

3.1.1 近地面风场和组合反射率结构的变化

图4给出了分析循环结束后各试验的近地面风场和组合反射率结构。由图可知,仅同化雷达径向风时,各同化试验在雷达回波较强区都有气流辐合,表明同化雷达径向风可有效提高风场结构从而改善模式大气动力状况。由组合反射率结构可知,同化雷达径向风基本可以反映台风的反射率结构,3DVar试验以及混合协方差试验(HybE0.25、HybE0.5和HybE0.75)与“真实场”符合较好,优于全集合协方差试验(Hyb1.0)。尽管Hyb1.0试验可以建立合理的台风结构但其组合反射率与“真实场”有较大区别,主要表现在台风外围虚假回波较多而中心区域回波强度弱于“真实场”。混合协方差试验与HybE1.0试验对比发现,静态背景误差协方差可以平滑掉因集合协方差的引入而带来的部分虚假分析增量。

3.1.2 误差演变的分析

对反射率因子大于10 dBz的对流区域格点计算先验和后验均方根误差(root mean square error,RMSE)分析同化效果好坏。图5给出各试验水平速度u、v,垂直速度w和位温θ的RMSE变化。由图可知,4个变量的RMSE随分析循环次数增加均有减小,当使用混合协方差时,同化效果优于3DVar试验,当集合协方差权重为1.0时,分析场最差。循环同化结束时刻,HybE0.75分析场效果最好。

结合离散度变化(图略)分析HybE1.0同化效果劣于3DVar的可能原因。HybE1.0试验里,所有变量离散度从第二个分析时次开始与其他权重系数试验拉开并逐渐变大。由于本次试验集合成员数为30,集合成员数过小可能导致预估的集合协方差不稳定或不可靠。当全采用集合协方差时,后验离散度可能虚假偏高致使分析场RMSE出现较大增加。混合协方差试验与全集合协方差试验对比说明:尽管预估的集合协方差可能不稳定,但在Hybrid EnSRF-En3DVar同化系统中,适当采用一个合理的集合协方差权重来增加“流依赖”协方差信息仍然是有益的。

3.2 反射率的影响

理论上,雷达径向风观测算子包含水平速度和垂直速度,同化径向风将有效改善大气的风场结构。反射率观测算子包含雨水混合比,这也将更有效地改善大气的湿度和热力结构。设置仅同化径向风及联合同化径向风和反射率的对比试验,分别从风场、湿度场和反射率的变化来分析同化不同雷达观测资料对Hybrid EnSRF-En3DVar同化系统的影响。由于本研究中全集合协方差试验效果有待提高,故集合协方差权重系数仅设置为0.25、0.5及0.75。

3.2.1 水汽结构的变化

图6为第一个分析时刻850 hPa水汽混合比变化及沿27°N水汽混合比垂直剖面。由图可知,联合同化径向风和反射率试验对大气湿度场有较好改善(图6a1—c1),而仅同化径向风试验水汽混合比增量只在台风中心附近有微小变化(图6a2—c2)。由水汽混合比垂直剖面图发现联合同化反射率和径向风试验里(图6a3—c3),121～125°E为水汽混合比增加区,水汽混合比增量强中心在900 hPa附近,最高可达300 hPa左右。而仅同化雷达径向风试验(图6a4—c4),水汽混合比整层仅有微量变化。由此可见,在水汽场调整上,联合同化反射率和径向风可有效改善大气湿度场,而仅同化径向风对大气湿度场的改变不大。

图5 台风对流区(反射率大于10 dBz)纬向速度u(a)、经向速度v(b)、垂直速度w(c)和位温θ(d)的均方根误差随时间的变化Fig.5 Evolution of RMSEs of (a)zonal speed(u),(b)meridional speed(v),(c)vertical speed(w),and (d)potential temperature(θ) in the typhoon convection area(reflectivity greater than 10 dBz)

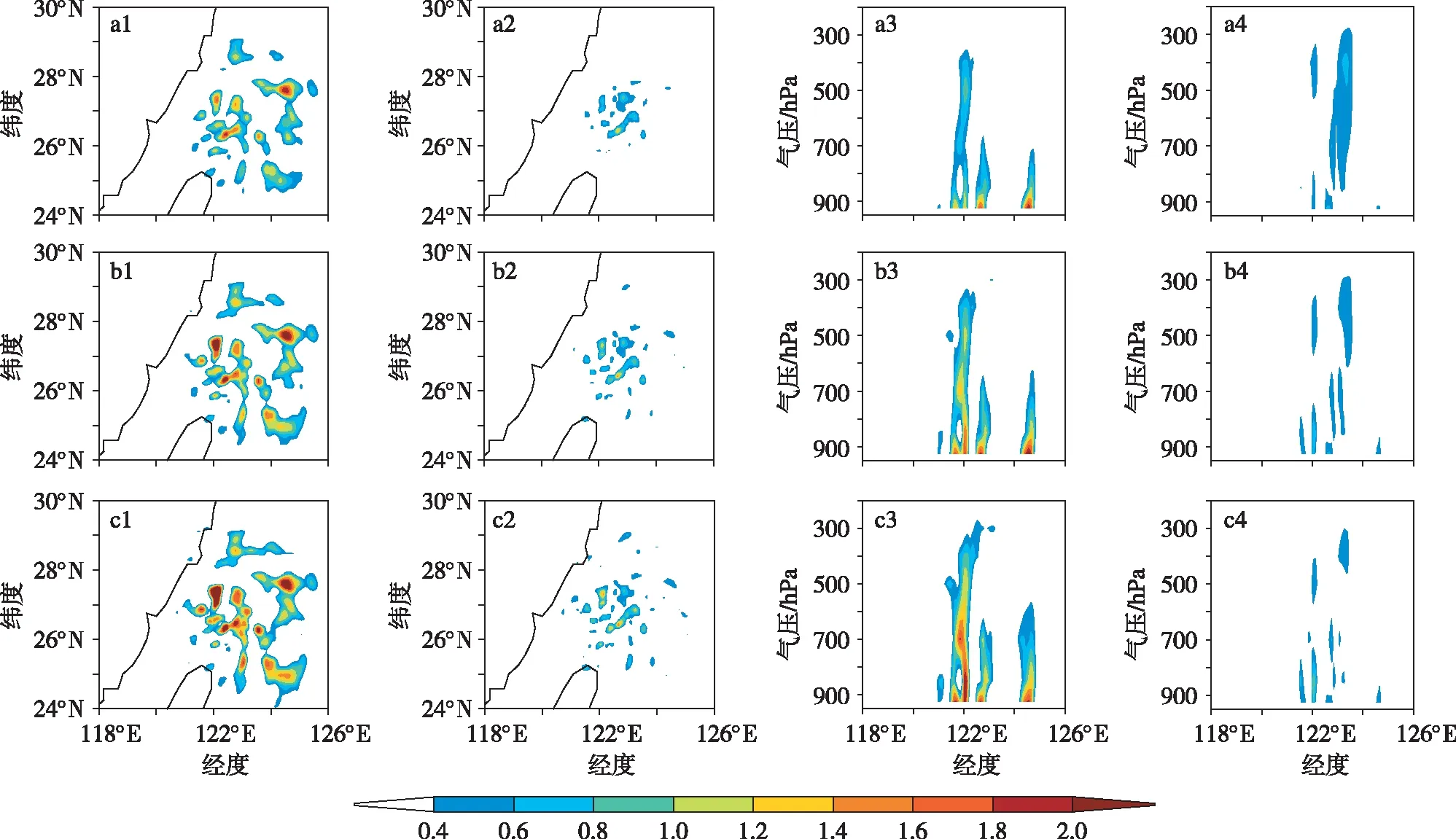
图6 2006年8月10日00时850 hPa水汽混合比的水平分布及沿27°N的垂直剖面(单位:g/kg;其中1、2为水平分布,3、4为垂直剖面) a1,a3.HybE0.25-RVRF;a2,a4.HybE0.25;b1,b3.HybE0.5-RVRF;b2,b4.HybE0.5;c1,c3.HybE0.75-RVRF;c2,c4.HybE0.75Fig.6 Horizontal distributions(1 and 2) and vertical profiles(along 27°N;3 and 4) of water vapor mixing ratio at 850 hPa at 0000 UTC 10 August 2006(units:g/kg) a1,a3.HybE0.25-RVRF;a2,a4.HybE0.25;b1,b3.HybE0.5-RVRF;b2,b4.HybE0.5;c1,c3.HybE0.75-RVRF;c2,c4.HybE0.75

3.2.2 误差演变的分析

图7给出了各模式变量的RMSE分布。对风场(u、v、w)和温度场(θ)进行分析发现,从循环同化开始至第4次分析循环,联合同化反射率和径向风试验效果优于仅同化径向风试验,之后时次仅同化径向风试验效果渐优,风场表现尤其明显。湿度场(qv)和反射率(Z)的分析发现,联合同化反射率和径向风试验的qv和Z均方根误差小于仅同化径向风试验。所有模式变量改进最明显的是反射率Z,反射率Z最佳估计由HybE0.25-RVRF给出。

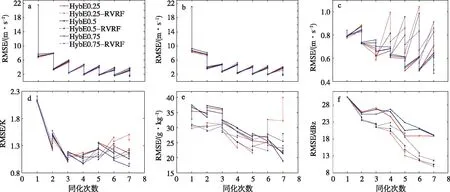
图7 台风对流区(反射率大于10 dBz)u(a)、v(b)、w(c)、θ(d)、qv(e)、Z(f)的均方根误差随时间的变化Fig.7 Evolution of RMSEs of (a)zonal speed(u),(b)meridional speed(v),(c)vertical speed(w),(d)potential temperature(θ),(e)qv,and (f)Z in the typhoon convection area(reflectivity greater than 10 dBz)

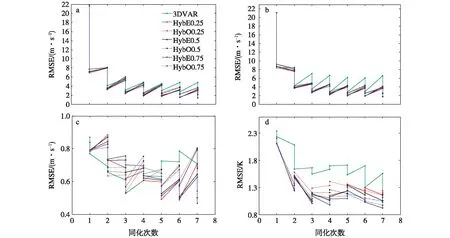
图8 台风对流区(反射率大于10 dBz)u(a)、v(b)、w(c)、θ(d)的均方根误差随时间的变化Fig.8 Evolution of RMSEs of (a)zonal speed(u),(b)meridional speed(v),(c)vertical speed(w),and (d)potential temperature(θ) in the typhoon convection area(reflectivity greater than 10 dBz)

图9 台风对流区(反射率大于10 dBz)u(a)、v(b)、w(c)、θ(d)的离散度随时间的变化Fig.9 Evolution of spreads of (a)zonal speed(u),(b)meridional speed(v),(c)vertical speed(w),and (d)potential temperature(θ) in the typhoon convection area(reflectivity greater than 10 dBz)

3.3 集合扰动更新方案的影响

在现有使用Hybrid方法同化雷达资料初始化台风的研究中,Li et al.(2012)在台风Ike的研究中利用PO-En3DVar同化雷达径向风。PO集合扰动更新方案需在原始观测基础上叠加随机扰动从而易引入新的采样误差。EnSRF作为一种确定性算法,不需事先对观测进行扰动,避免引入额外误差。为详细讨论上述两种集合扰动更新方案对Hybrid同化效果的影响,设置以下试验(表1中1—4、9—11)分别同化雷达径向风进行对比。

3.3.1 误差演变的分析

图8给出了各同化试验u、v、w和θ的均方根误差演变。由图可知,两种集合扰动更新方案同化效果均优于3DVar试验,尤其是温度场(θ)。由于本组试验仅同化雷达径向风,并未同化与温度相关的变量,说明“流依赖”集合误差协方差的引入能够正确反映物理量的相关关系并且有效地改进模式分析场。

对比EnSRF方案和PO方案发现,EnSRF方案前期在每次分析过程中并没有明显的减少分析误差,但随着同化时间的延长,EnSRF方案的优势逐渐明显。此外,循环同化后期EnSRF方案在同化过程中误差的增长速度要明显低于PO方案。分析发现可能原因是PO方案集合扰动的更新仅在观测上叠加随机扰动得到,而EnSRF方案更新的集合扰动具有动力约束,得到的分析场在动力上更协调从而减小了分析误差。

3.3.2 离散度变化

雷达探测的主要是天气系统发展最不稳定的对流区域,当含有中尺度信息的雷达资料进入模式,分析场在观测空间表现为离散度随循环同化逐渐增加,最后增长率达到饱和。离散度大小并不能直接反应同化效果的好坏,但如果离散度过小,背景误差协方差被低估导致分析场过度依赖背景场,易造成“滤波发散”(闵锦忠等,2013)。由图9各变量先验、后验离散度可以看出,PO方案虽然可以吸收观测信息,但随着循环同化时间的延长,其集合成员离散度振幅和数值过小,后期预报容易造成“滤波发散”。EnSRF方案不仅可以准确地捕获到雷达观测的中小尺度信息,也使集合离散度维持在适当范围内。

4 结论与讨论

基于WRF模式,使用EnSRF方案直接更新集合扰动并结合En3DVar构建了Hybrid EnSRF-En3DVar同化系统。利用构建的同化系统针对台风“桑美”分别进行了集合协方差权重敏感性试验和同化雷达不同观测资料的敏感性试验。此外,将EnSRF集合扰动更新方案与现有Hybrid雷达资料研究中常用的扰动观测集合扰动更新方案进行对比,探讨了两种集合扰动更新方案对Hybrid同化效果的影响。试验表明:

1)当集合协方差权重分别为0.25、0.5和0.75时,同化效果优于3DVar试验;当集合协方差权重为1.0时,分析场最差;循环同化结束时刻,集合协方差权重为0.75时分析场最优。

2)仅同化雷达径向风能有效地将中小尺度信息加入到风场结构中,但对大气湿度场和热力场的改变不大。联合同化雷达反射率及径向风能有效改善大气湿度场和热力场,但对风场的改善效果不如仅同化雷达径向风试验。

3)扰动观测集合扰动更新方案集合离散度较小,后期容易造成“滤波发散”。从实际执行效果看,由于要分别更新集合成员,计算代价大。综合分析发现,EnSRF集合扰动更新方案优于扰动观测集合扰动更新方案。

本文观测系统模拟试验说明,Hybrid EnSRF-En3DVar同化系统同化模拟雷达资料能有助于初始化台风,为下一步真实多普勒雷达观测资料在台风的初始化和集合预报的研究工作提供了技术支撑。由于本次试验目的是验证Hybrid EnSRF-En3DVar同化系统的可行性,为节省计算资源,集合成员数取30。Gao and Stensrud(2014)指出,当集合成员数过小时,全采用集合协方差会因为预估的集合协方差不稳定造成分析后离散度虚假偏高,导致分析效果变差。下一步利用真实多普勒雷达观测资料初始化台风的研究工作中将增加集合成员数,验证全集合协方差试验的同化效果是否有所改进。

陈杰,闵锦忠,王世璋,等.2012.WRF-EnSRF系统同化多普勒雷达资料在多类型强对流天气过程的数值试验[J].大气科学学报,35(6):720-729. Chen Jie,Min Jinzhong,Wang Shizhang,et al.A numerical experiment on WRF-EnSRF for assimilation of Doppler Radar in multicase strong convective weather process[J].Trans Atmos Sci,35(6):720-729.(in Chinese).

陈耀登,王元兵,闵锦忠,等.2014.一种控制变量循环扰动和多参数化方案的混合同化方法[J].大气科学学报,37(6):732-739. Chen Yaodeng,Wang Yuanbing,Min Jinzhong,et al.2014.A hybrid assimilation method with control variable cycle perturbation and multi-physical parameterization[J].Trans Atmos Sci,37(6):732-739.(in Chinese).

Dowell D,Zhang F,Wicker L,et al.2004.Wind and temperature retrievals in the 17 May 1981 Arcadia,Oklahoma,supercell:Ensemble Kalman filter experiments[J].Mon Wea Rev,132(8):1982-2005.

Gao J,Stensrud D J.2014.Some observing system simulation experiments with a hybrid 3DEnVAR system for storm-scale radar data assimilation[J].Mon Wea Rev,142(9):3326-3346.

耿建军,肖现,王迎春,等.2012.变分多普勒雷达分析系统对北京一次强降水过程的短时预报能力初探[J].大气科学学报,35(6):730-736. Geng Jianjun,Xiao Xian,Wang Yingchun,et al.2012.A preliminary exploration on the nowcasting ability of VDRAS in a rainstorm case in Beijing[J].Trans Atmos Sci,35(6):730-736.(in Chinese).

Hamill T M,Snyder C.2000.A hybrid ensemble Kalman filter-3D variational analysis scheme[J].Mon Wea Rev,128(8):2905-2919.

Li Y,Wang X,Xue M.2012.Assimilation of radar radial velocity data with the WRF hybrid ensemble-3DVAR system for the prediction of Hurricane Ike(2008)[J].Mon Wea Rev,140(11):3507-3524.

Liu S,Xue M,Gao J,et al.2005.Analysis and impact of super-obbed Doppler radial velocity in the NCEP grid-point statistical interpolation (GSI) analysis system[C]//17th Conf on Num Wea Pred.Washington:Amer Meteor Soc.

Lorenc A.2003.The potential of the ensemble Kalman filter for NWP-a comparison with 4DVar[J].Quart J Roy Meteor Soc,129(595):3183-3204.

闵锦忠,毕坤,陈耀登,等.2013.基于物理约束扰动的EnSRF雷达资料同化[J].大气科学学报,36(2):129-138. Min Jinzhong,Bi Kun,Chen Yaodeng,et al.Study of assimilating Doppler radar data with EnSRF based on physical constraint perturbation[J].Trans Atmos Sci,36(2):129-138.(in Chinese).

Parrish D F,Derber J C.1992.The national meteorological center’s spectral statistical interpolation analysis system[J].Mon Wea Rev,120(8):1747-1763.

Sun J,Crook N A.1997.Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint.Part I:Model development and simulated data experiments[J].J Atmos Sci,54(12):1642-1661.

王顺凤,蔡春园,沈桐立,等.一次暴雨过程的变分同化试验及诊断分析[J].大气科学学报,2011,34(2):153-161. Wang Shunfeng,Cai Chunyuan,Shen Tongli,et al.Variational assimilation and diagnosis of a rainstorm process[J].Trans Atmos Sci,2011,34(2):153-161.(in Chinese).

Wang X,Barker D M,Snyder C,et al.2008a.A hybrid ETKF-3DVAR data assimilation scheme for the WRF model.Part Ⅰ:Observing system simulation experiment[J].Mon Wea Rev,136(12):5116-5131.

Wang X,Barker D M,Snyder C,et al.2008b.A hybrid ETKF-3DVAR data assimilation scheme for the WRF model.Part Ⅱ:Real observation experiment[J].Mon Wea Rev,136(12):5132-5147.

Whitaker J S,Hamill T M.2002.Ensemble data assimilation without perturbed observations[J].Mon Wea Rev,130(7):1913-1924.

Zhang F,Snyder C,Sun J.2004.Impacts of initial estimate and observation availability on convective-scale data assimilation with an ensemble Kalman filter[J].Mon Wea Rev,132(5):1238-1253.

Zou X L,Xiao Q N.2000.Studies on the initialization and simulation of a mature hurricane using a variational bogus data assimilation scheme[J].J Atmos Sci,57(3):836-860.

(责任编辑：刘菲)

Study on the assimilation of Doppler radar data using a hybrid EnSRF-En3DVar method

MIN Jin-zhong1,LIU Sheng-yu1,2,BI Kun3,DU Ning-zhu1

(1.Key Laboratory of Meteorological Disaster(NUIST),Ministry of Education,Nanjing 210044,China;2.Unit 94833,PLA,Nanchang 330201,China;3.Unit 94608,PLA,Nanjing 210022,China)

A hybrid ensemble square root filter and three-dimensional ensemble-variational(EnSRF-En3DVar) data assimilation system is developed based on WRF model.The EnSRF is used to update ensemble perturbations in this system.Aiming at Typhoon Saomai,two sets of sensitivity experiments are conducted to test this system.One is choosing different weight coefficients of ensemble covariance,the other is assimilating radar radial velocity(Vr) and/or reflectivity(Z).The first set of experiments is to answer how the flow-dependent covariance estimated from the forecast ensemble works best in the hybrid EnSRF-En3DVar system.The results show that the assimilation effects from experiments with 30 ensemble members and ensemble covariance weight coefficients of 0.25,0.5 and 0.75 are better than those from 3DVar experiment.The best(worst) one is from the experiment when weight coefficient of ensemble covariance is 0.75(1.0).The second set of experiments is to examine the impact of assimilating radarVrand/orZon the analysis using EnSRF-En3DVar system.The results show that the combined assimilation ofVrandZcan improve the initial analysis of humidity and wind fields,but the only assimilation ofVrcan improve the analysis of wind field most.Finally,the methods to generate the ensemble perturbations are compared.The results show that the “perturbed observation” method gives smaller ensemble spread and needs more expensive computational cost than the EnSRF method.

data assimilation;Hybrid EnSRF-En3DVar;Doppler radar;typhoon

2015-01-04；改回日期：2015-03-24

国家重点基础研究发展计划(973计划)项目(2013CB430102);中国气象局武汉暴雨研究所暴雨开放基金项目(HR2008K01)

闵锦忠,博士,教授,博士生导师,研究方向为中小尺度数值模拟与资料同化、风暴尺度集合预报及气候变化区域响应,minjz@nuist.edu.cn.

10.13878/j.cnki.dqkxxb.20150104008.

1674-7097(2015)02-0213-09

P459.9

A

10.13878/j.cnki.dqkxxb.20150104008

闵锦忠,刘盛玉,毕坤,等.2015.基于Hybrid EnSRF-En3DVar的雷达资料同化研究[J].大气科学学报,38(2):213-221.

Min Jin-zhong,Liu Sheng-yu,Bi Kun,et al.2015.Study on the assimilation of Doppler radar data using a hybrid EnSRF-En3DVar method[J].Trans Atmos Sci,38(2):213-221.(in Chinese).