某异形人行桥的人致振动分析

李志刚

(中交第二公路勘察设计研究院有限公司，湖北　武汉　430056)

某异形人行桥的人致振动分析

李志刚

(中交第二公路勘察设计研究院有限公司，湖北武汉430056)

李志刚(1984—)，男，助理工程师，主要研究方向为桥梁设计。

摘要：文章以一座异形钢结构人行桥为例，应用通用有限元软件ANSYS对其进行数值模拟，并基于强迫振动理论和随机振动理论，对该桥BS5400单人荷载模式和三种随机行人荷载工况下的结构响应进行人致振动分析，结果表明该桥满足相关国外规范对于人行桥舒适性的要求。

关键词：异形人行桥；人致振动；单人荷载模式；随机行人荷载；分析

0引言

随着人们对于人行桥等公共设施舒适、美观等环境质量要求的不断提高，仅考虑人行桥结构安全性已经不够，基于功能的理念才更能符合时代的要求。因此，人行桥的舒适性要求也是一个需要重点考虑的内容。然而，我国对人行桥的使用性问题还不够重视。现行的我国人行桥规范只是简单地通过限制结构基频>3 Hz和静力挠度不超过跨径的1/800来保证，这种衡量方法已很难适应现代人行桥的设计。相比而言，部分国家的规范则对人行桥的使用性方面已有了更加深入和具体的规定。除了设置更为严格的基频限值以保证人行桥的使用性外，它们还提出对于不满足基频限值的桥梁，应采用动力响应分析法评估结构的动力使用性能，规定桥梁结构在人行荷载作用下产生的动力响应不应超过相应的舒适度界限值(一般采用加速度响应的最大值或均方根值)。如英国规范BS5400[1]和欧洲规范Eurocode 5：Annex B规定竖向基频<5 Hz的人行桥需要验算其动力使用性能。在结构动力响应分析方面，英国规范和加拿大规范OHBDC通过计算一个匀速移动的简谐荷载作用下的结构最大响应来评估人行桥的舒适性，欧洲规范则建议对复杂的结构形式进行更精细的数值分析。

本文以一座异形钢结构人行桥为背景，通过有限元软件ANSYS对其进行数值模拟，结合国外规范对人行桥舒适性的规定，对该桥开展基于强迫振动理论和基于随机振动理论的人致振动分析，考查该人行桥的动力使用性能，就人行桥人致振动分析方法进行一些探讨。

1虹桥的概况及数值模型

虹桥是湖南省常德市白马湖公园内的一座人行桥，全长120 m，宽5.5 m，跨径组合为(27+33+33+27)m；主梁线型为“S”形，主梁采用全焊接闭口钢箱梁截面，桥塔为高20 m的“帆”形钢塔，在桥塔与主梁曲线内侧间呈“扇”形布置空间斜拉索，在墩台顶及桥塔侧面均布置聚四氟乙烯板式橡胶支座。虹桥总体布置见图1。

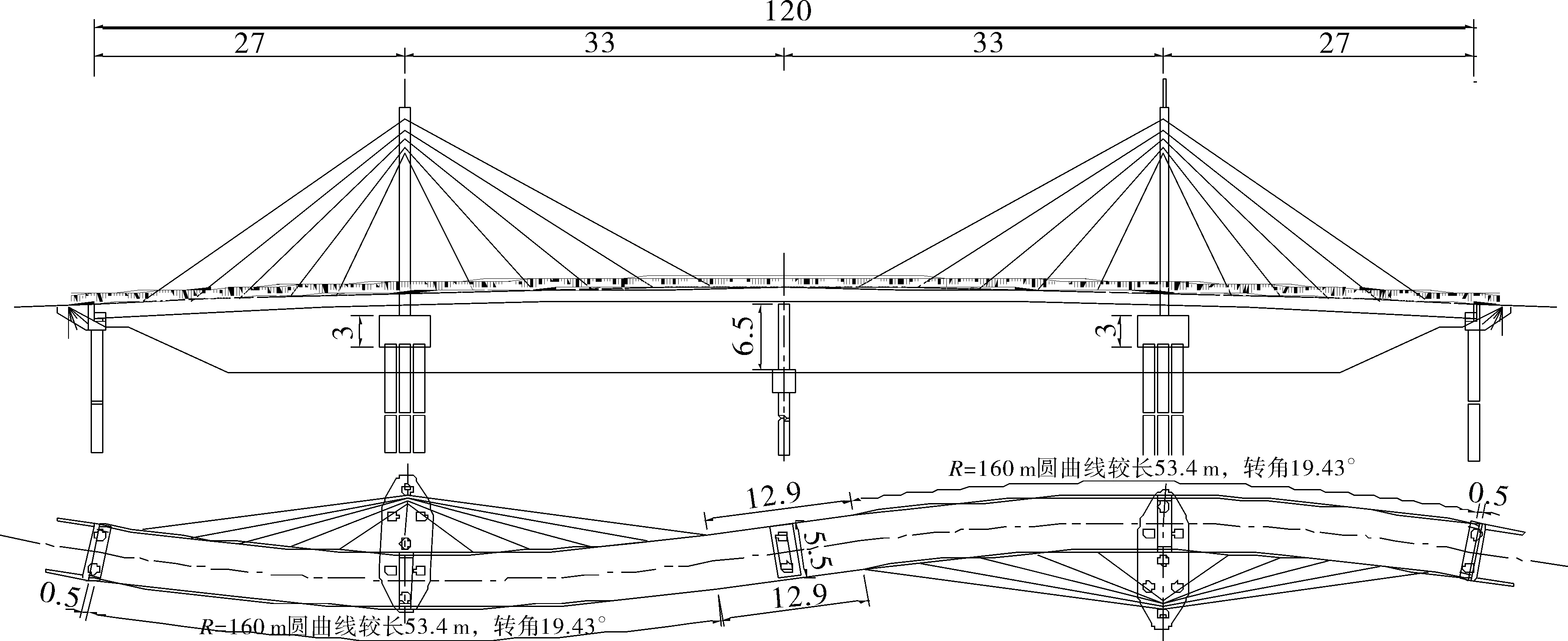
图1　虹桥总体布置图

用ANSYS软件对该桥进行数值模拟时，主梁采用在“鱼骨梁”两侧添加有质量的外侧虚梁的方式建模，外侧虚梁的质量来源于栏杆与栏杆基座质量的等效。中心主梁采用beam188单元，桥塔、桥墩、刚臂与外侧虚梁均采用beam4单元；拉索采用link10仅受拉、压杆单元；锚箱用mass21质量单元模拟；支座均采用combin14弹簧单元模拟；桥塔、桥墩、桥台底均作为固结处理。全桥空间有限元模型如图2所示。

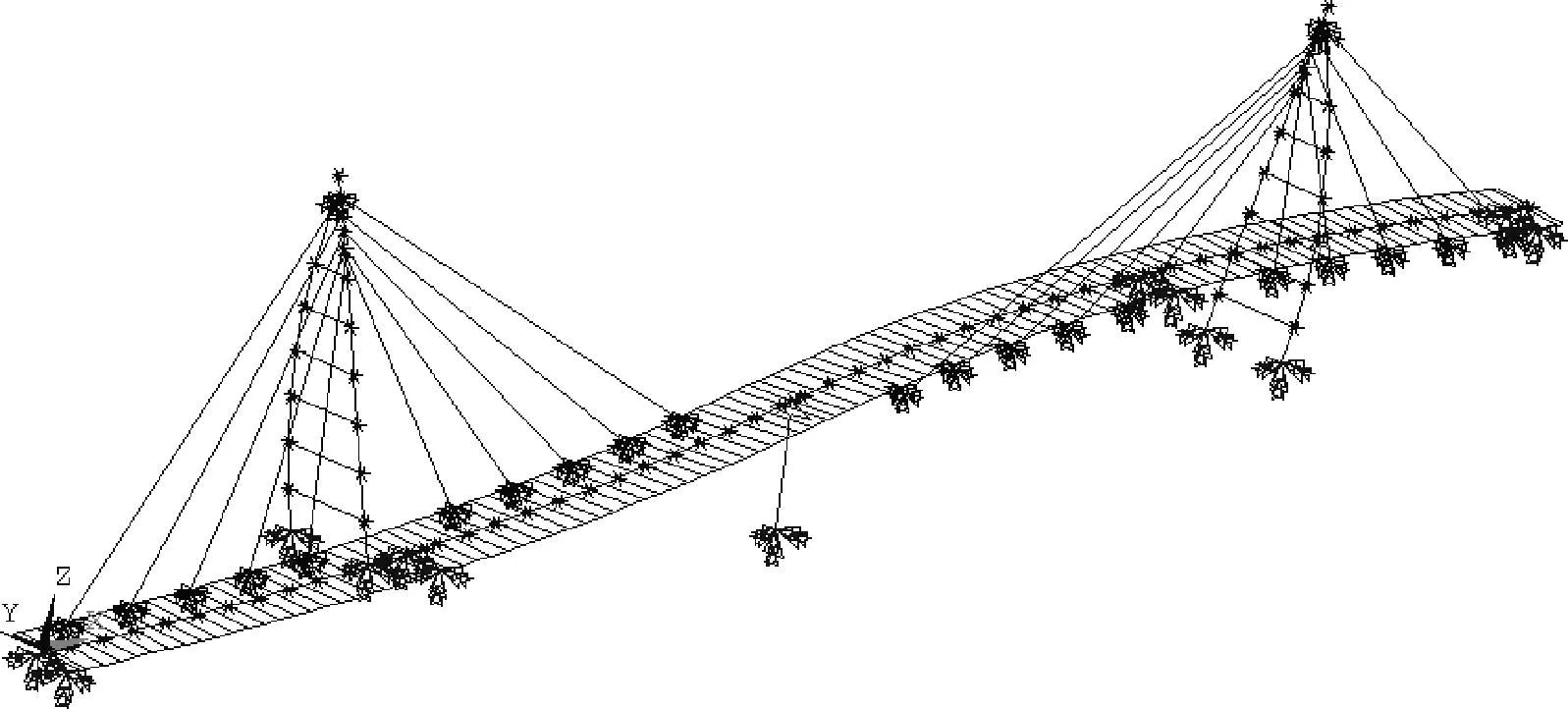
图2　虹桥有限元模型图

进行虹桥模态分析时，质量矩阵采用一致质量矩阵，模态提取方法采用分块兰索斯法，计算得前几阶频率和振型特征如表1所示。

表1　虹桥自振频率与振型特征表

2人行桥人致振动分析基本理论

绝大多数情况下人行桥的人致振动响应呈弹性，属于线性振动问题，因此可以用模态分解的方法计算人行桥的振动响应。人行桥的人致振动微分方程可以表达为：

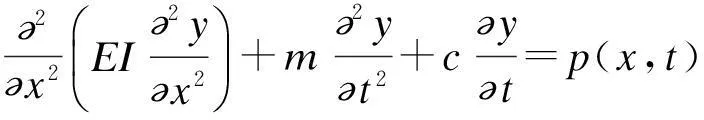
(1)

引入广义坐标Yn(t)，以及相应的振型函数φn(x)，运用振型叠加法有：

(2)

将式(2)代入(1)，根据振型的正交性将振动微分方程解耦得到：

(3)

人行荷载是一种具有近似周期性的随机移动荷载，与其它桥梁的动力响应问题相比，人行桥人致振动问题的特殊性在于激振的荷载是人。人致振动分析理论对应于分析时采用的不同的人行荷载模型，笼统地可以概括为自激振动理论、参数振动理论、强迫振动理论以及随机振动理论四种。自激振动理论和参数振动理论主要针对跨度大的柔性人行桥或者横向刚度很小的人行桥在行人激励下出现横向动力失稳的问题，虹桥的动力特征表明其不在这两种理论的适用范围内。因此本文的重点是结合相关规范和理论，对虹桥进行基于强迫振动理论和随机振动理论的人致振动分析。

3基于强迫振动理论的虹桥人致振动分析

由于人行荷载具有近似周期性的特征，如果将单个人行荷载用多个谐波组成的傅立叶级数的形式来表示，那么人行桥人致振动的问题则可以简化为多阶谐波作用下的强迫振动问题。由于人群荷载高阶谐波的同步调特征很小，人行荷载在分析时可只考虑前两阶谐波成分(竖向频率约为一阶1.6~2.4Hz，二阶3.2~4.8HZ，水平向的为竖向的一半)。如果人行桥的固有频率在前两阶谐波荷载频率范围内，与桥梁固有频率接近的谐波荷载将在激振时起决定性作用，人致振动分析的问题则可简化为单自由度共振的问题。人行谐波荷载的竖向力和水平力可以表示为：

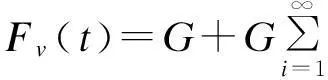
(4)

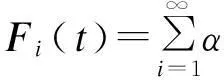
(5)

式中G为行人的体重；fp为行人的步频；αvi和αli分别是竖向力与侧向力的第i阶谐波动载因子，即谐波的幅值与行人体重之比；φvi和φli分别为竖向力与水平力的第i阶谐波相位角[2]。

国外的设计规范大多是基于移动简谐荷载作用下的简支梁振动理论给出的人行桥舒适度的分析方法，采用单人共振荷载验算桥面最大加速度响应。本文采用英国规范BS5400提出的用移动点荷载F(t)，沿着桥梁以恒定的速度向前运动产生的最大加速度响应来评估桥梁的动力使用性能。其中：

F(t)=180sin(2π×f0t)[N]

(6)

vt=0.9f0[m/s]

(7)

图3　中跨跨中竖向加速度时程曲线图

4基于随机振动理论的虹桥人致振动分析

用傅立叶级数的形式来表示人行荷载的基础是把人行荷载当作理想的周期荷载，但实际的人行荷载是呈空间分布的随机荷载，人的位置、人的重量、步频、步行相位等都是随机变量，想要求解结构更贴合实际的响应则需采用基于随机振动理论的方法。当不考虑由于人桥相互作用而引起步行同步的情况时，桥上行人可以认为处在自由行走状态，行人荷载可以直接用Monte-Carlo法模拟其随机特征，从而对结构进行人行荷载激励下的动力响应时程分析。

在虹桥基于随机振动理论的人致振动分析中，利用人行荷载的傅里叶级数表达式，按照一定的概率分布形式用Monte-Carlo法生成随机的步行荷载。计算时参照德国规范提供的行人交通级别和行人密度，将人群荷载分为三种工况。工况一行人密度为0.2人/m2，桥上共计120人；工况二行人密度为0.5人/m2，桥上共计300人；工况三行人密度为1.0人/m2，桥上共计600人。其中工况一和工况二行人为自由行走状态，步行速度按正常步速取为1.5 m/s；工况三由于行人密度大，行人间存在相互影响的情况，据Fujino[5]对日本户田公园人行桥的观测结果，考虑20%的行人荷载同步调，同时将步行速度取值降低为1.2 m/s。

单人步行力考虑前两阶的谐波荷载，第i个行人的竖向力可表示为：

Fi(t)=Gi(α1sin(2π×fit+φ1i))+α2sin(4π×fit+φ2i))δ(x-xi-vt)N

(8)

式中：

(1)行人体重Gi，根据Tuan and Saul[6]以及Ebrahimpour and Sack[7]的研究，按服从均值为700 N，标准差为145 N的正态分布取值；

(2)步频fi，根据Matsumoto[8]的研究，按服从均值为2.0 Hz，标准差为0.173 Hz的正态分布取值；

(3)初始相位φ1i、φ2i，对于完全的随机步行，按服从(0，2π)间的均匀分布取值；

(4)初始位置xi，由于行人在桥上出现的位置机会均等，因此按服从(0，120 m)间的均匀分布取值；

(5)动载因子α1、α2，按照Bachman等[9]的研究，α1取为0.37，α2取为0.10。

对于工况三中行人荷载同步调的情况，采用20%的行人以2.0Hz的步频同相位通过虹桥的方式模拟，G取值为700 N，初始相位均取为0，初始位置在24 m范围内服从均匀分布；其它行人按随机荷载模拟。分析时取前200阶振型采用振型叠加法进行计算，荷载步间隔时长取为0.02 s，采用循环加载的方式使得行人刚下桥就马上上桥以保证桥上行人的数量，阻尼考虑为常阻尼，阻尼比取值采用实测的0.413%。限于篇幅列出工况一中跨跨中竖向加速度时程曲线如图5所示，工况二中跨跨中竖向加速度时程曲线如图6所示，工况三中跨跨中竖向加速度时程曲线如图7所示。计算得工况一主梁最大加速度为0.358 m/s2，工况二主梁最大加速度为0.309 m/s2，工况三主梁最大加速度为0.680 m/s2。

图5　工况一中跨跨中竖向加速度时程曲线图

图6　工况二中跨跨中竖向加速度时程曲线图

图7　工况三中跨跨中竖向加速度时程曲线图

参照德国规范，各工况需达到的舒适级别和最大竖向加速度响应限值如表2所示[4]。

表2　各工况对应的加速度限值表

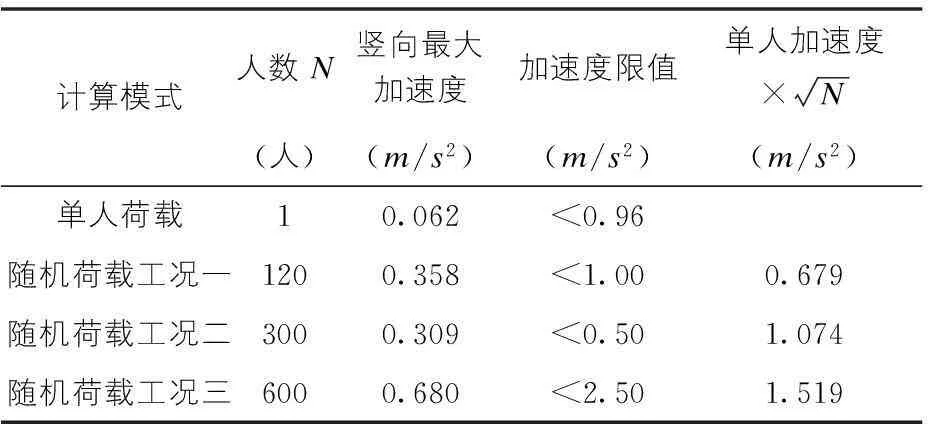
表3　虹桥人致振动加速度汇总表

5结语

(1)本文分别用强迫振动理论和随机振动理论对虹桥进行人致振动分析，结果表明虹桥的人行舒适性满足使用要求。

(2)单人荷载模式与随机荷载模式下计算得到的最大加速度对比分析表明，英国规范BS5400采用的单人荷载模式评定舒适度的方法的适用范围有待考查；而由于运用随机理论进行人致振动分析往往耗时费力，能广泛运用于工程实际的简便方法有待研究。

参考文献

[1]BD29/04.Design Manual for Road and Bridges：Design Criteria for Foot bridges[S].London：Highway Agen-ey，2004.

[2]Bachmann H.Case Studies of Structures with main-induced Vibrations[J].Journal of Structural Engineering.1992，118(3)：631-647.

[3]Matsumoto Y，Nishioka T，Shiojiri H，Matsuzaki K.Dynamic Design of Footbridges[C].IABSE Proceedi-ngs，1978.

[4]陈政清，华旭刚.人行桥的振动与动力设计[M].北京：人民交通出版社，2009.

[5]Fujino Y，Pacheco BM，Nakamura SI，Wamitchai P.Synchronization of human walking observed during lateral vibration of a congested pedestrian bridge[J].Earthquake Engineering & Structural Dynamics.1993，22(9)：741-758.

[6]Tuan CY，Saul WE .Loads due to Spectator Movements[J].Journal of Structural Engineering，ASCE，1985，111(2)：418-434.

[7]Ebrahimpour A，Sack RL.Design Live Loads for Coherent Crowd Harmonic Movements[J].Journal of Structural Engineering，ASCE，1992，110(2)：401-418.

[8]Matsumoto Y，Sato S，Nishioka T，Shiojiri H.A Study on Design of Pedestrian Over-Bridges[J].Transactions of JSCE，1972，4：50-51.

[9]Bachmann H，Ammann W.Vibrations in Structures Induced by Man and Machines[M].IABSE：IABSE-AIIPC-IVBH，1987.

Human-induced Vibration Analysis of A Special-shaped Footbridge

LI Zhi-gang

(CCCC Second Highway Consultants Co.，Ltd.，Wuhan，Hubei，430056)

Abstract：With a special-shaped steel pedestrian bridge as the example，this article used the finite ele-ment software ANSYS for its numerical simulation，and based on forced vibration theory and random vibration theory，it conducted the human-induced vibration analysis on the structural response under the work conditions of BS5400 single-person load mode and three random pedestrian loads of this bridge，the results showed that this bridge can meet the requirements of relevant foreign norms for footbridge comfort.

Key Words：Special-shaped footbridge；Human-induced vibration；Single-person load mode；Random pedestrian load；Analysis

收稿日期：2015-02-05

文章编号：1673-4874(2015)02-0025-05

中图分类号：U448.11

文献标识码：A

DOI：10.13282/j.cnki.wccst.2015.02.007

作者简介