基于高分辨率卫星的影像预处理研究
2015-03-16王义
王 义
(中铁二院工程集团有限责任公司,四川成都 610031)
Research on Preprocessing of High Resolution Satellite Image
WANG Yi
基于高分辨率卫星的影像预处理研究
王义
(中铁二院工程集团有限责任公司,四川成都610031)
Research on Preprocessing of High Resolution Satellite Image
WANG Yi
摘要通过研究高分辨率卫星影像预处理技术流程,研发相应预处理软件,完成影像灰度拉伸、降位、裁剪及旋转等预处理工作,增强影像对比度及减小卫星影像数据量,提高影像清晰度及电脑运行速度。
关键词卫星影像降位裁剪 灰度拉伸旋转
随着航空航天技术的发展,利用高分辨率卫星影像测制中小比例尺地图成为可能。高分辨率卫星影像信息量丰富,但多为16位,数据量较大,电脑处理速度较慢,影响生产效率;且原始影像灰度较暗,不便于观察作业。因此,需要对原始高分辨率卫星影像进行预处理。
介绍高分辨率卫星影像灰度拉伸、降位、裁剪、及旋转等预处理的技术流程,并阐述基于该技术流程开发的预处理软件的实现思路。
1卫星影像预处理流程
卫星影像预处理流程如图1。

图1卫星影像预处理流程
卫星影像的处理涉及到影像及RPC参数(有理多项式模型系数)的处理,影像灰度拉伸及降位处理与影像几何坐标无关。不处理RPC参数,裁剪和旋转过程影像像素坐标会改变,RPC参数文件必须修改成与之匹配。
1.1 灰度拉伸及降位处理
卫星影像数据一般以16位存储,其亮度与对比度较小,需要作适当增强。增强软件较常用的有PhotoShop、Eardas等,本文以Photoshop为例。
利用PhotoShop打开卫星影像,选择调整自动对比度功能,屏幕上反映的全黑影像经过灰度拉伸后,地形及地物要素立刻显示出来。对粗调的灰度曲线作精细人工调整,以保证立体像对的两幅影像在反差上尽量一致,方便观察。经灰度调整后的图像,在PhotoShop中选择8位/通道模式,该步骤将16位影像降为8位,降位后的影像数据量减少一半,但几何精度不变,随着影像数据量的减少,提高了电脑运行速度。值得注意的是,灰度拉伸及降位处理两步骤顺序不能颠倒,如颠倒顺序调整,影像灰度会失真。
本课题将灰度拉伸及降位合为一个步骤,简化了作业过程,从而提高生产效率。
1.2 卫星数据的旋转
卫星影像多为同轨成像模式,为了恢复立体模型,一般需对影像及RPC参数作90°旋转。通过自主开发系统实现影像快速重采样,旋转并重新计算RPC参数。
(1)图像旋转
图像旋转是指图像以某一点为中心旋转一定的角度,形成一幅新的图像的过程。这个点通常就是图像的中心,既然是按照中心旋转,自然会有这样一个属性:旋转前和旋转后的点离中心的位置不变。
根据这个属性,可以得到旋转后点的坐标与原坐标的对应关系。由于原图像的坐标是以左上角为原点的,所以先把坐标转换为以图像中心为原点。假设原图像的宽为w,高为h,(x0,y0)为原坐标内的一点,转换坐标后的点为(x1,y1)。那么可得到
在新的坐标系下,假设点(x0,y0)距离原点的距离为r,点与原点之间的连线与x轴的夹角为b,旋转的角度为a,旋转后的点为(x1,y1), 如图2所示。
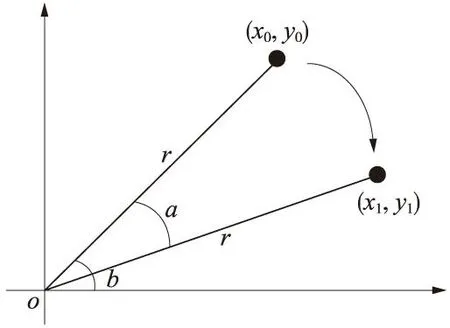
图2 图像旋转示意
以此得出结论
x0=rcosb;y0=rsinb
x1=rcos(b-a)=rcosbcosa+rsinbsina=
x0cosa+y0sina;
y1=rsin(b-a)=rsinbcosa-rcosbsina=
-x0sina+y0cosa;
从而得到了转换后的坐标,只需要把这些坐标再转换为原坐标系即可。旋转后的图像长和宽会发生变化,因此要计算新图像的长和宽。旋转90°是该模型的一个特例,将角度代入公式可计算旋转后的像素坐标。
(2)RPC参数变换
RPC为卫星公司提供的有理函数模型系数,反映了卫星影像像点坐标与其对应的地面点之间的变换关系。
RPC参数变换采用二维至三维格网映射变换算法:
可以在原有影像上编制一个格网,例如10×10像素,通过有理多项式将每个格网点的地面坐标求出来。影像旋转之后,通过新的图像坐标(像元)与物方空间的WGS84坐标E,N,H的对应关系计算出新的有理多项式系数。
已知地面某点物方空间的WGS84坐标E,N,H,通过有理多项式可求出其对应点的图像坐标(像元)。具体变换如下:
物方坐标规格化(Normalize)
(1)
(2)
(3)
式中:
LONG_OFF,LONG_SCALE:为参数文件所提供的物方规格化参数;
E,N,h:为物方地面点在WGS84椭球体中的坐标;
En,Nn,hn:为地面点的规格化的坐标。
由物方空间坐标到像方坐标转换的逻辑流程如图3。
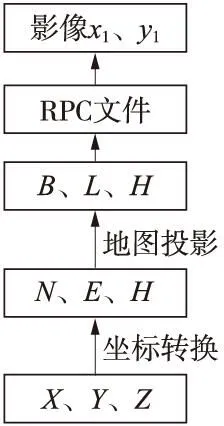
图3 物方空间坐标到像方坐标转换的逻辑流程
成影变换—有理多项式变换原理计算法如下:
物方点通过有理多项式变换获得基本图像上的点位,即像方坐标
(4)
(5)
式中:a0……d19为参数文件中提供的有理多项式参数;xn,yn为图像上对应点的规格化坐标。
规格化图像坐标到图像坐标的变换如下式
(6)
(7)
式中:x,y为像点的坐标,左上角为0,单位为pixel;xn,yn为规格化坐标;SAMP_SCALE,……为像方规格化参数。
从两像方坐标解求物方坐标,即已知同名像点P1(xl,yl),P2(xr,yr)求解其物方点坐标(E,N,h)。
(8)
(9)
其矩阵表达式为
(10)
即
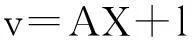
(11)
立体像对可得到四个方程,法化方程为
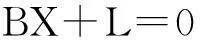
(12)
解之可求得改正数:ΔE,ΔN,Δh。
可分别选取LONG_OFF、CAT_OFF、HEIGHT_OFF为E0、N0、h0的初值,反复迭代,直至改正数Δ<σ。
由像方空间坐标到物方坐标转换的逻辑流程如图4所示。
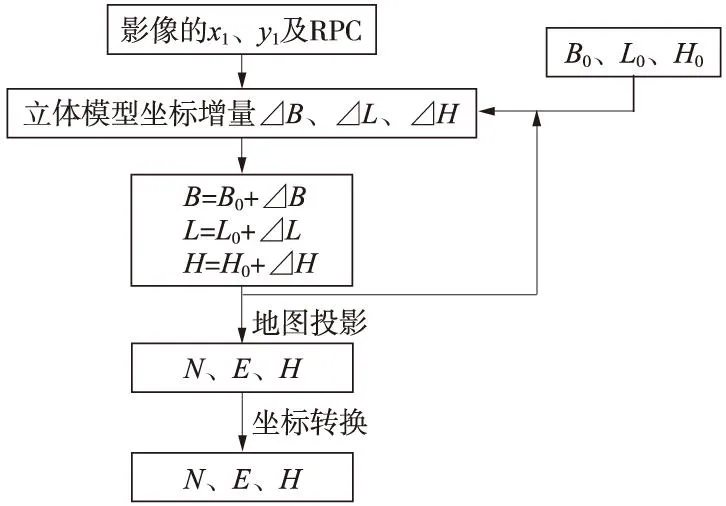
图4 由像方空间坐标到物方坐标转换的逻辑流程
计算旋转后的系数,将其写入RPC文本文件,完成RPC参数修改。
2卫星数据的裁剪
卫星影像及其参数的裁剪相对于旋转实现起来要简单一些。
带RPC参数的遥感影像裁切,要保证裁切后的数据中卫星参数起算点的经纬度不发生变化,也就是说,要解算出源影像的参数中心在目标影像中的位置(如图5)。
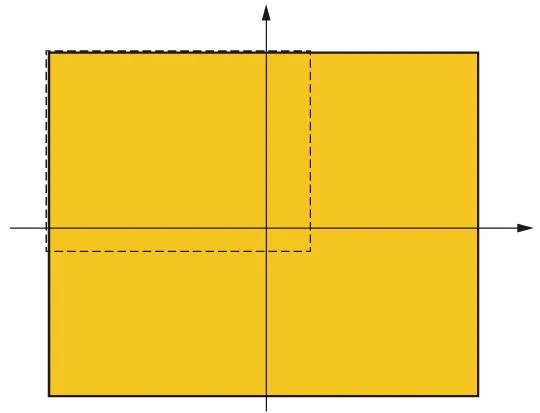
图5 卫星影像裁剪示意
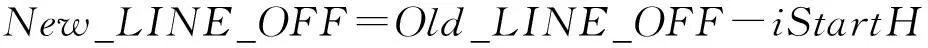
(13)
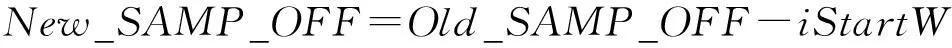
(14)
其中iStartH,iStartW是裁图起始点在源影像上的坐标。
3卫星影像预处理系统的实现
通过分析卫星影像灰度拉伸、降位、旋转及裁剪等实现原理,利用VS2010开发工具,完成卫星影像预处理系统的开发。该系统在打开卫星影像过程中同时生成金字塔影像,可实现影像多倍放大及缩小功能,方便后续处理,并引入了大影像缓存技术,缩短了下次打开影像的时间;预处理系统还具有批处理功能,可以同时处理多幅影像,并且处理速度较快。图6为卫星影像预处理系统操作界面。
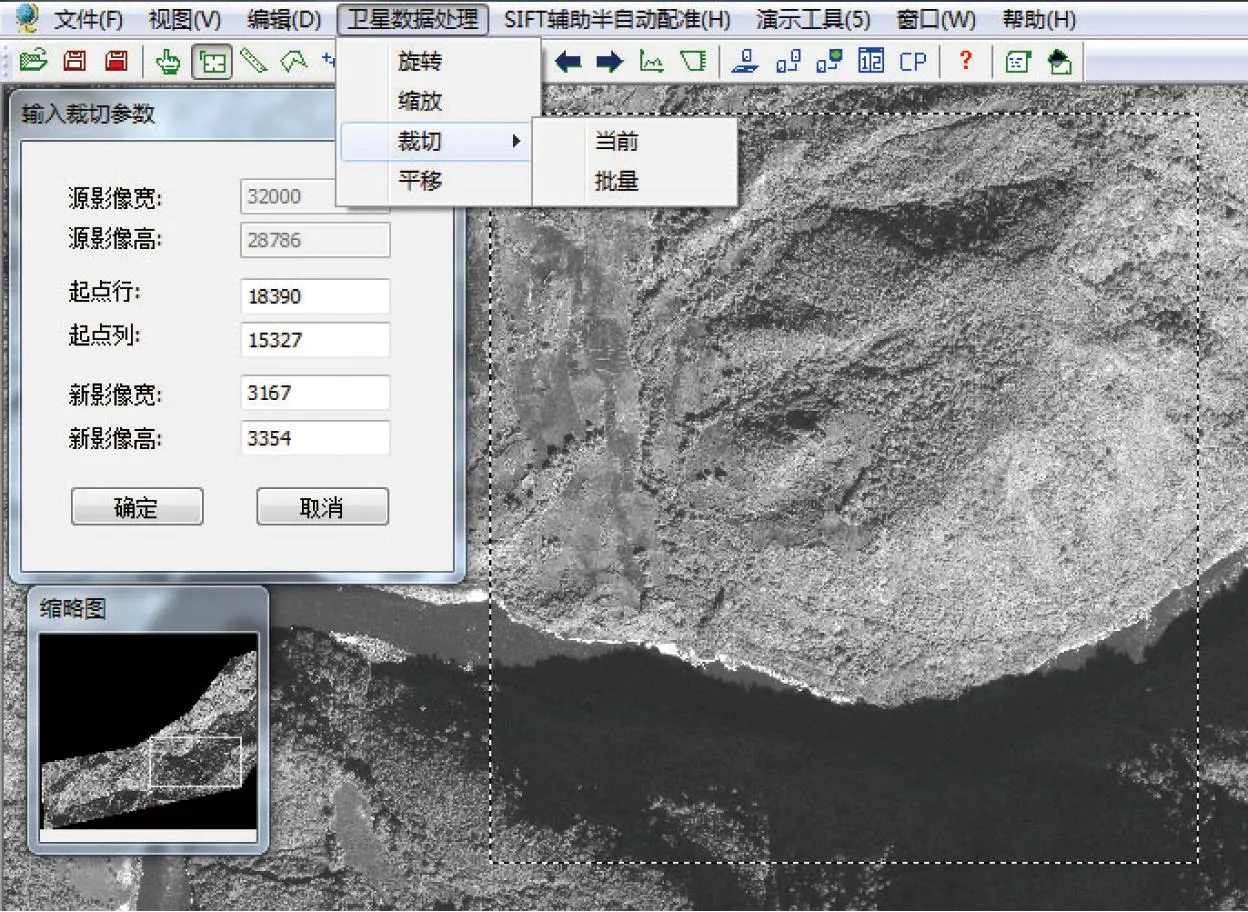
图6 卫星影像预处理系统界面
4卫星预处理后精度检核
卫星影像灰度拉伸及降位处理,只涉及到影像的辐射信息,与几何坐标无关,不影响精度,但影像旋转及裁剪涉及到几何位置改变,所以要对其旋转和裁剪后的精度作验证。卫星影像作预处理后,通过JX4G、MapMatrix等全数字摄影测量工作,恢复立体模型,经立体检查无上下视差,检查控制点定向精度报告,并通过外业实测散点检查制图精度,表1、表2、表3为某国外铁路利用WorldView2立体定向及实测散点检查精度报告。
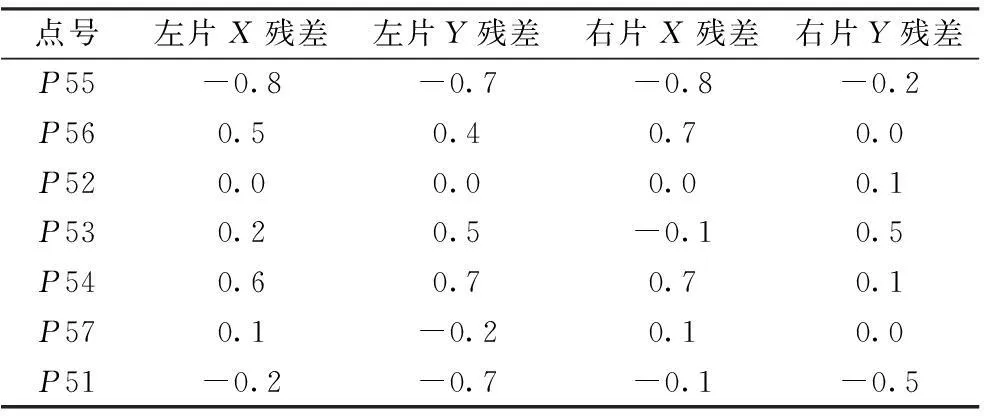
表1 卫星影像立体像对定向像点坐标残差 像素
通过多个项目实践,本课题研究的卫星影像预处理系统,精度可靠,且处理方法简单实用,值得推广应用。

表2 定向控制点的残差和均方根中误差 m
5结论
为了解决高分辨率卫星影像灰度较暗、数据量较大及同轨影像不旋转90°不易配成立体等问题,开发了卫星影像预处理系统,通过对影像进行灰度拉伸、降位、同轨影像旋转90°及裁剪,提高了影像处理速度,方便了人眼观察,具有较大的创新实用性。
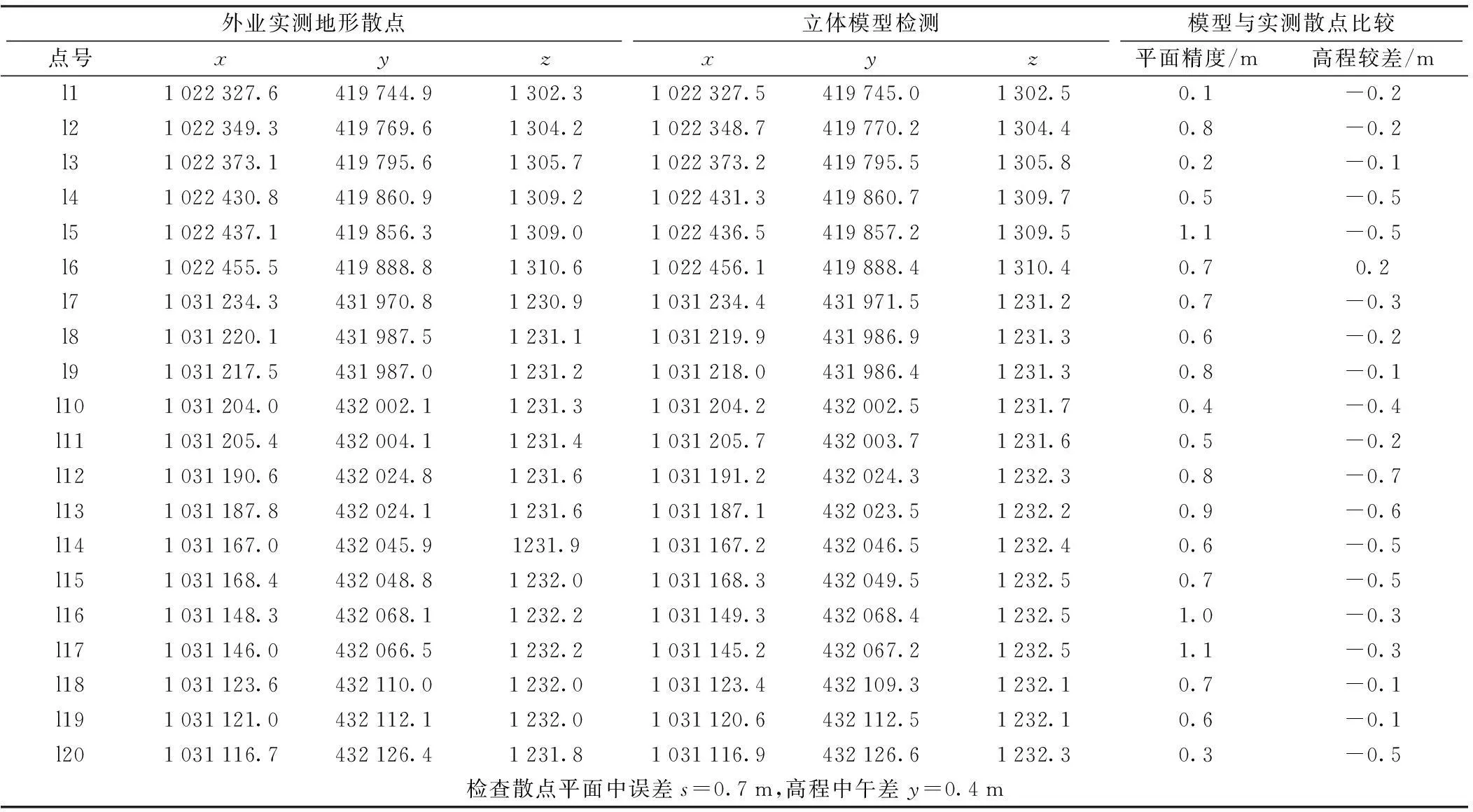
表3 实测散点与立体模型量测较差及中误差 m
参考文献
[1]孙家抦.遥感原理与应用[M].武汉:武汉大学出版社,2013
[2]李兵,朱继东,陈艳.采用IKONOS卫星影像进行立体测图技术的应用研究[J].地理信息世界,2006(12)
[3]张燕,王国昌,王智,等.IKONOS-2立体像对的纠正精度分析[J].铁道勘察,2009(3)
[4]王国昌.卫星影像制图在铁路勘测设计中的应用研究[J].铁道工程学报,2010(2)
[5]代强玲,王智,闵世平.GeoEye-I卫星影像制图在铁路勘测设计中的应用[J].铁道勘察,2014(3)
[6]刘凤德,赵利平,李健.基于JX4C的IKONOS的一体化处理[J].测绘科学,2008(2)
[7]周云.高分辨率卫星影像数据与LIDAR数据在铁路勘测设计中的深度应用[J].铁道勘察,2012(1)
[8]蒋勇.各种卫星影像数据在铁路勘测中的应用[J].铁道勘察,2013(5)
[9]龚明劼,张鹰,张芸.卫星遥感制图最佳影像空间分辨率与地图比例尺关系探讨[J].测绘科学,2009(4)
[10]张永生,刘军.高分辨率遥感卫星立体影像RPC模型定位的算法及其优化[J].测绘工程,2004(1)
中图分类号:P237
文献标识码:B
文章编号:1672-7479(2015)04-0011-04
作者简介:王义(1975—),男,2000年毕业于武汉测绘科技大学摄影测量与遥感专业,工学学士,高级工程师。
收稿日期:2015-05-28
