大孔隙扭曲度对土壤水分入渗的影响

张少妮, 徐学选,, 高朝侠, 宇苗子, 赵传普

(1.西北农林科技大学 水土保持研究所, 陕西 杨凌712100; 2.中国科学院 水利部

水土保持研究所, 陕西 杨凌 712100; 3.西北农林科技大学 资源环境学院, 陕西 杨凌 712100)

大孔隙扭曲度对土壤水分入渗的影响

张少妮1, 徐学选1,2, 高朝侠2, 宇苗子3, 赵传普2

(1.西北农林科技大学 水土保持研究所, 陕西 杨凌712100; 2.中国科学院 水利部

水土保持研究所, 陕西 杨凌 712100; 3.西北农林科技大学 资源环境学院, 陕西 杨凌 712100)

摘要：[目的] 探究大孔隙扭曲度对土壤水分入渗的影响，为深入了解大孔隙扭曲度影响优先流的物理机制提供理论依据。[方法] 采用室内含大孔隙土柱的定水头入渗试验，以长武地区黑垆土为研究对象，分析大孔隙不同扭曲度对土壤湿润锋运移、累积入渗量和水分穿透时间的影响。[结果] 大孔隙的形状深刻影响入渗湿润锋的形状，对湿润锋纵向、横向运移具有引导作用；大孔隙扭曲度减小可加速湿润锋运移，增加累计入渗量；水分穿透土柱的时间随扭曲度的增大而增加，穿透时间与扭曲度可用对数关系描述;湿润锋运移深度、累积入渗量与时间均呈明显的乘幂关系，其函数式的参数取决于土体中大孔隙扭曲度。 [结论] 大孔隙扭曲度对水分入渗影响深刻，是研究大孔隙流的重要因素。

关键词：大孔隙扭曲度; 湿润锋; 累积入渗量; 穿透时间

大孔隙流是土壤水分优先流现象的一种，它是指水分沿着植物根系路径、蚯蚓孔洞、狭长裂隙等大孔隙运动的非平衡流，水流绕过结构密实、渗透率低的土壤基质，优先通过导水能力强的大孔隙通道而快速下渗[1]。土壤大孔隙中水分运动与溶质运移现象，在19世纪中后期就被发现，但直到20世纪70年代末Thomas和Phillips[2]，以及Beven和German[3]的研究才引起更多学者对大孔隙流的关注。近些年，大孔隙形态学逐渐成为研究的重点，包括大孔隙度、平均长度、平均扭曲度等研究内容。大孔隙的扭曲度属于大孔隙空间网络参数，出于不同的研究目的，学者采用不同的公式表示扭曲度[4-5]。由于天然状态下，大孔隙的扭曲度受多因素影响，对其的研究比较复杂，为了简化扭曲度的研究，有学者将人造大孔隙放置于回填土柱中进行供水试验来研究大孔隙的特性[6-7]，并取得了一定的成果。Allaire等[7]通过土壤水分穿透曲线来研究大孔隙的扭曲度，指出大孔隙的扭曲度必须建立在连通性(与土壤表面连通)存在的情况下才对水分入渗有作用(因为只有与土壤表面连通的大孔隙才能起到水分的传导作用)，而且扭曲度主要影响水分及溶质在土壤剖面的分布。Schwen等[8]指出土壤中生物活动可以增加大孔隙的连通性，降低孔隙的扭曲度。也有学者指出大孔隙的粗糙度越大，扭曲度越大，连通性越小[9-10]。Arora等[11]研究指出大孔隙域与基质域交界面的水力特性是大孔隙扭曲度、界面饱和导水率和其他界面参数的一个函数。以上研究表明影响大孔隙扭曲度的因素较多，孔隙的扭曲度与连通性都影响到土壤入渗能力，大孔隙扭曲度对于水分及溶质运移的过程机理因其本身的复杂性而需要更多的试验研究。因此，本研究在借鉴前人研究成果的基础上，利用含人工大孔隙土柱入渗的方法，研究不同扭曲度下大孔隙流的湿润锋运移、最小穿透时间、累积入渗量等入渗特征，以期深入了解大孔隙扭曲度影响优先流的物理机制。

1材料与方法

1.1　试验土壤

采集陕西省长武县塬区耕层0—60 cm黑垆土土壤，将土样去除杂质、碾碎，自然风干，过2 mm筛，土壤机械组成结果详见表1。

表1　供试土样机械组成

1.2　试验装置与方法

试验装置由供水系统、土柱箱以及收集系统3个部分组成，供水系统由马氏瓶(Φ=8 cm)提供2.5 cm的恒定水头，精度为0.1 cm。土柱箱由厚1 cm的有机玻璃制成，规格为30 cm×2 cm×70 cm(长×宽×高)。本试验土柱的高度为60 cm。装土前在玻璃容器底部铺一层滤纸，避免土壤粉末堵塞出流孔或从出流孔中漏出，滤网上面加入一层3 cm石英砂作为反滤层。对欲安装大孔隙的土柱，应根据孔隙位置先安装大孔隙再装土，保证土样和大孔隙之间的密实。装样结束后在土柱上部放一薄层石英砂(1 cm)做缓冲层，防止进水时顶部的土样被冲掉。顶部用宽塑料胶带粘贴覆盖以防止蒸发。土柱底部开孔(Φ=0.5 cm)，开孔密度为1孔/cm2,防止水分在土柱底部累积。收集系统是由厚度为0.8 cm的PVC漏斗制成，自由排出的水分流经塑料烧杯进行收集。

试验时黑垆土的初始含水率为3.01%，控制容重为1.3 g/cm3。选择不锈钢丝网[12](60目)来制作大孔隙，这是因为60目的不锈钢丝网与土壤的孔隙相近，能起到侧渗的作用，更好地贴近实际情况。将不锈钢钢丝网卷在一根2 mm的铁丝上，然后再用纱布缠绕，最后将2 mm的铁丝抽掉，制作成为总直径为5 mm的大孔隙，按照大孔隙设计类型制作成不同的形状。试验布设5种大孔隙和1个没有大孔隙的对照组(CK)，大孔隙的长度均为30 cm，其形状或摆放位置存在差异，每种布设方式设置3个重复。试验设计中的6种大孔隙布设类型分别对应不同梯度大小的孔隙扭曲度，扭曲度定义为孔隙长度与孔隙深度的比值[11，13]。根据扭曲度定义可知，笔直的孔隙扭曲度为1，除此之外其它孔隙的扭曲度均大于1，无空隙的扭曲度为∞。土柱中大孔隙的布设状况如图1所示，扭曲度用Ti表示，i表示扭曲度值大小。试验过程中，记录马氏瓶中水面的高度，前10 min每1 min记录1次，10～30 min每5 min记录1次，30～60 min每10 min记录1次，60 min后每20 min记录1次。湿润锋根据土壤入渗特性每隔5～20 min采用数码相机拍照，直至土柱底部每隔20 min出流体积连续5次相同即可停止试验。

2结果与分析

2.1　大孔隙扭曲度对湿润锋运移形态的影响

室内试验获取的照片，经Erdas 9.2几何校正和ArcGIS 9.3编辑处理，不同扭曲度下的大孔隙流湿润锋随时间的变化情况如图1所示。由图1可以看出，大孔隙扭曲度会深刻影响水分在土壤中的分布。大孔隙对于湿润锋在纵向和侧向上的运移均具有引导作用。在入渗10 min时，从水分运移的侧向来看，T∞的湿润锋在水平方向上几乎呈直线；其余几组的湿润锋形状在大孔隙处出现不同程度的凹陷，而且沿孔隙左右两侧出现不同程度的侧渗。在纵向上，随着扭曲度的增大，湿润锋的最大入渗深度是减小的。总之，在入渗10 min时，水分基本上沿着大孔隙提供的路径运移，扭曲度越大，土壤水分纵向运移越小，横向运移越大。

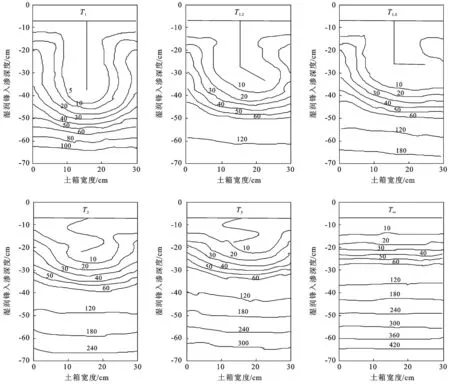
注：与横线相连的是大孔隙，与竖轴相连的是湿润锋。T为扭曲度，i为扭曲度值的大小。

大孔隙的扭曲方向会影响局部的水分入渗。在30 min时，湿润锋的形状较10 min逐渐趋于平缓，但是其影响依旧存在。具体表现为湿润锋运移沿大孔隙向两侧继续侧渗，T1很明显可以看出湿润锋沿大孔隙的对称性。T3和T2的大孔隙呈S形，由于大孔隙的扭曲方向不同(大孔隙均表现为先向左扭动，后向右扭动)，湿润锋的左侧高于右侧，即右侧入渗的快，说明大孔隙的扭曲方向会影响水分的分布，影响湿润锋的形状。而从T1.5和T1.2中，更容易看出右侧的湿润锋运移快于左侧(大孔隙下部向右侧扭曲)。因此，横向的大孔隙对于湿润锋的运移也有一定的促进作用。在60，120 min时，随着时间的延长，大孔隙域逐渐失去纵向入渗的作用，在横向水势梯度下拉动了水分的横向运移，湿润锋形状逐渐趋于水平，呈现整体性稳步向下推移。湿润锋运移速率初期较快，之后逐渐减小至稳定。出现以上现象的原因主要是由于在入渗初期，土壤含水量低，入渗边界与湿润锋之间形成较高的水势梯度，湿润锋的推进速率较快；随着时间的延长，湿润体内含水量增大，水势梯度明显减小，导致湿润锋向下推移速度减缓。大孔隙扭曲度越小，土壤入渗界面承受的压力势瞬时增大，湿润锋的推进速度越快。扭曲度增大，水流所受的阻力加大，一定程度上降低了湿润锋的推进速度。综合分析认为，大孔隙扭曲度深刻的影响着初期土壤水分的分布及整个湿润锋的推进速度，在模拟土壤水分入渗时，必须考虑大孔隙形状对水分运移的影响。

2.2　大孔隙扭曲度对湿润锋运移速度的影响

为了定量分析大孔隙扭曲度对湿润锋的影响程度，将每个时间段的湿润锋深度平均化，得到大孔隙不同扭曲度下湿润锋深度随时间的变化曲线(图2)。由图2可知，T1入渗最快，T∞入渗最慢，说明对于同样长度的大孔隙，随着扭曲度增大，湿润锋运移减慢；扭曲度减小，湿润锋运移加快。土体中大孔隙越陡直，水分沿大孔隙运动时与大孔隙间的摩擦阻力越小，水分入渗越快，湿润锋运移越快；大孔隙越扭曲，水分沿大孔隙运动时所受的阻力越大，水分入渗越慢，湿润锋运移越慢。

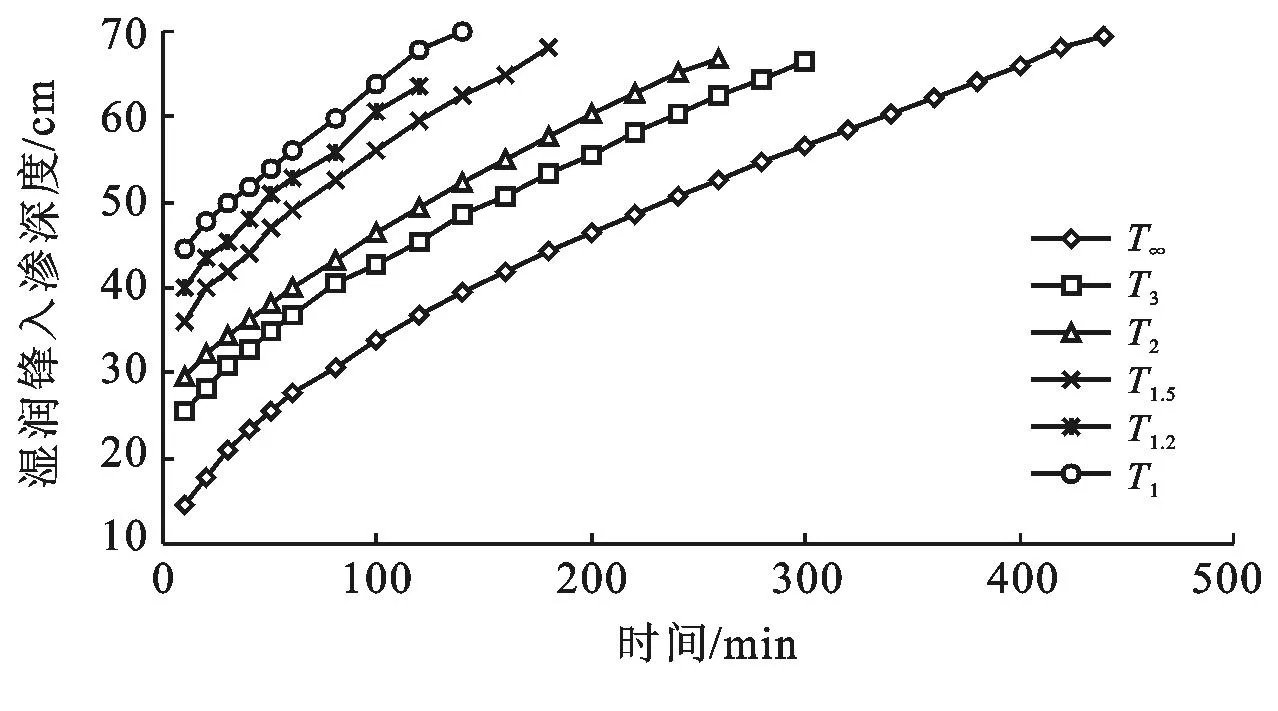
图2　不同扭曲度下优先流湿润锋入渗深度随时间的变化

湿润锋深度(Zf)随时间(t)的变化可以用幂函数进行拟合(Zf=atb)，拟合参数结果详见表2。由表2可看出,可用幂函数模拟不同扭曲度下湿润锋最大入渗深度，参数a值随着大孔隙扭曲度的减小而增大，参数b随大孔隙扭曲度的减小而减小。

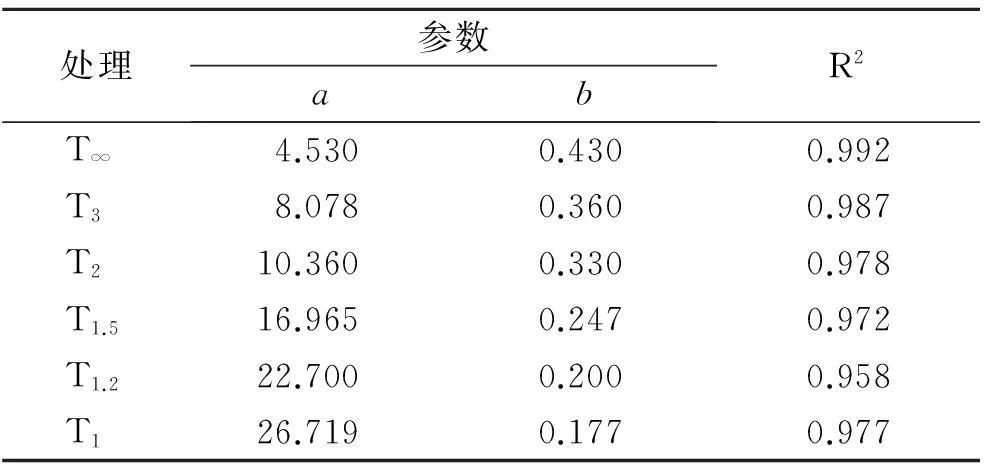
表2　不同扭曲度大孔隙湿润锋最大

试验中唯一变量是大孔隙的扭曲度，通过拟合扭曲度与参数a和参数b的关系，发现参数a,b与大孔隙扭曲度分别呈幂函数相关和对数相关。拟合结果分别为：

a=26.679T-1.571，T>1

(1)

b=0.1801lnT+0.177 1，T>1

(2)

式中：a——模型拟合的参数；b——模型拟合的参数；T——扭曲度。

结合Zf=atb得到湿润锋最大入渗深度于扭曲度的函数关系：

Zf=26.679T-1.571t0.180lnT+0.177 1，

T>1，R2>97.00%

(3)

式中：Zf——湿润锋入渗深度(cm)；t——时间(min)；T——扭曲度。

2.3　大孔隙扭曲度与穿透时间的关系

穿透时间是指水流穿透土柱的最小用时，即底孔开始出流的时间。土柱大孔隙扭曲度与水分穿透时间的关系对数函数进行很好的拟合(R2=0.960 5)。可以看出，扭曲度越大，穿透时间越长。这是由于相同长度的大孔隙，其扭曲度越大，说明其孔隙深度越小，说明其经过的土柱越浅，继而存在优先流的区域越小，穿透一定高度的土柱所需要的时间也会越长。

2.4　大孔隙扭曲度对累积入渗量的影响

图3为不同大孔隙扭曲度下累积入渗量随时间的变化曲线。在前50 min，累计入渗量增加速率由大至小依次为：T1>T1.2>T1.5，T2>T3>T∞，说明前50 min内，累计入渗量随着扭曲度的增大而减小，即扭曲度越小，此段时间内的入渗量越大，扭曲度越大，此段时间的入渗量越小；而在50 min后，大孔隙所在土层，已经完全浸湿，进入到无大孔隙介质层，单位时间入渗量趋于稳定，而累计入渗量呈现出稳定增长的趋势，而其增长幅度远小于有大孔隙时的增加量。在全部入渗时段，累积入渗量随大孔隙扭曲度增加均表现为减少趋势。其原因在于，对于相同长度的大孔隙，扭曲度越小，说明孔隙越陡直，水分在沿重力方向(孔隙方向)上受到的阻力越小，越有利于水分的下渗。而扭曲度越大，说明大孔隙弯曲的程度越大，其在沿重力方向入渗时，受到的阻力越大，水分下渗速率下降。

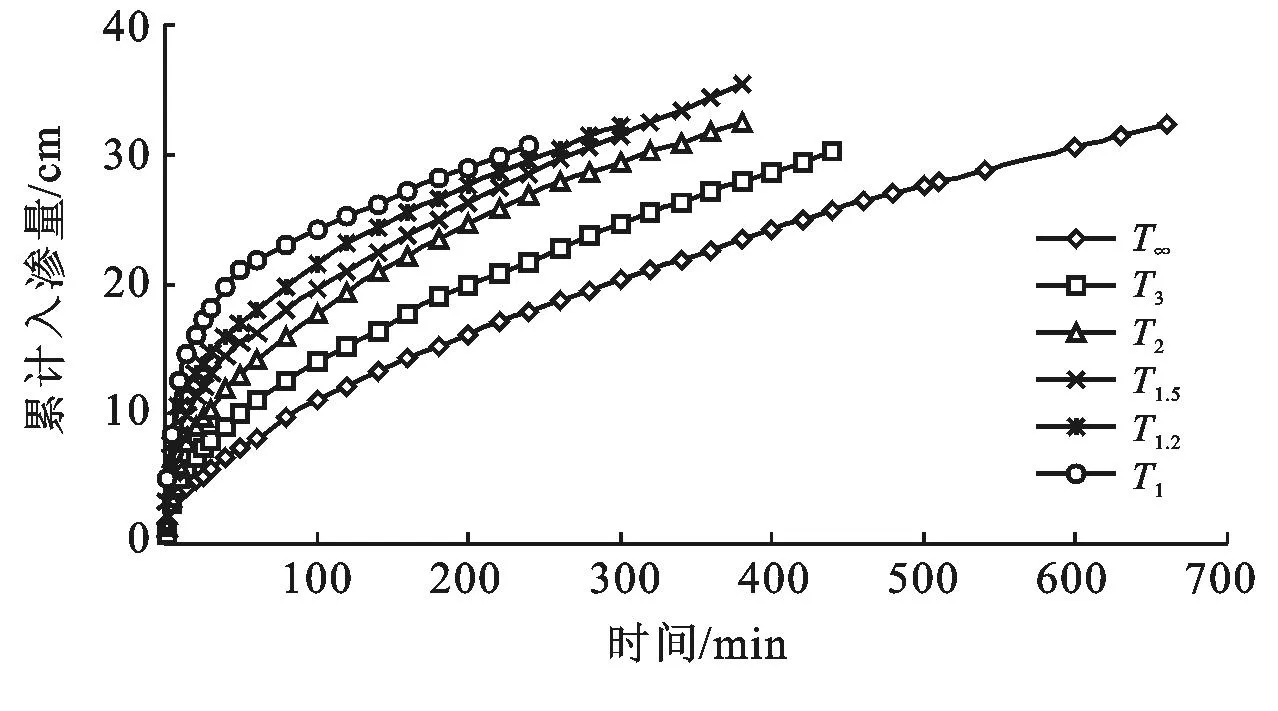
图3　扭曲度对累积入渗量的影响随时间的变化

为定量分析大孔隙扭曲度对优先流累积入渗量的影响，采用Kostiakov入渗模型不同扭曲度的大孔隙整个入渗过程的累积入渗量数据进行分析。Kostiakov入渗模型认为累积入渗量和时间呈幂函数关系，即

I=mtn

(4)

式中：I——累积入渗量(cm)；t——入渗时间(min)；m,n——模型参数。

经过拟合累计入渗量随时间的变化关系得出各个扭曲度下的m，n，R2值(表3)。从表3可以看出，相关系数均大于0.98，说明Kostiakov入渗模型拟合大孔隙流累计入渗量的方法可行。同时，参数m随着扭曲度的变化较大，呈现出随着扭曲度的减小逐渐增大的趋势。n随着扭曲度波动较小，但是依旧能体现出其随着扭曲度的减小逐渐减小的趋势。

试验中唯一变量是大孔隙的扭曲度，通过拟合扭曲度与参数m和参数n的关系，发现参数m和n与大孔隙扭曲度分别呈幂函数相关和对数相关。拟合结果分别为：

m=5.952 6T-1.408 1，T>1

(5)

n=0.202 8lnT+0.304 0，T>1

(6)

结合I=mtn得到累计入渗量与扭曲度的函数关系：

I=26.679T-1.408 1t0.202 8ln(T)+0.304 0

T>1，R2>99.30%

(7)

式中：I——累计入渗量(cm)；t——时间(min)；T——扭曲度。

表3　不同扭曲度下累计入渗量随时间变化模型拟合

3结 论

(1) 大孔隙的形状对于湿润锋运移的形状影响较为明显，大孔隙的扭曲方向深刻影响着湿润锋的形状，当湿润锋运行到大孔隙之下深度时，湿润锋形状逐渐趋于直线，形如无大孔隙存在的T∞。

(2) 大孔隙扭曲度对于湿润锋的最大入渗深度影响明显。扭曲度越大，湿润锋运移的最大深度就越小。湿润锋运移深度与时间具有乘幂函数关系。

(3) 大孔隙的扭曲度对水分穿透土柱时间具有显著影响。大孔隙扭曲度越大，穿透土柱用时越长，基本呈现对数函数关系

(4) 大孔隙扭曲度对于累计入渗量的影响可用类似Kostiakov入渗模型描述。扭曲度越大，一定时间内的累计入渗量越小；扭曲度取代了Kostiakov入渗模型中的m，n参数。

[参考文献]

[1]冯杰，解河海，黄国如，等. 土壤大孔隙流机理及产汇流模型[M].北京：科学出版社，2012.

[2]Thomas G W, Phillips R E. Consequences of water movement in macropores[J]. Journal of Envirnmental Quanlity, 1979, 8(2):149-152.

[3]Beven K, German P. Macropores and water flow in soils[J]. Water Resources Research, 1982, 18(5):1311-1325.

[4]Bear J. Dynamics of Fluids in Porous Media[M]. New York: Elsevier, 1972.

[5]Mualem Y, Dagan G. Hydraulic conductivity of soils: Unified approach to the statistical models[J]. Soil Science Society of America Journal, 1978, 42(3): 392-395.

[6]Czapar G F, Horton P, Fawcett R S. Herbicide and tracer movement in soil columns containing an artificial macropore[J]. Journal of Environmental Quality, 1992,21(1):110-115.

[7]Allaire-Leung S E， Gupta S C， Moncrief J F. Water and solute movement in soil as influenced by macropore characteristics (2): Macropore tortuosity[J]. Journal of Contaminant Hydrology, 2000,41(3/4):303-315.

[8]Giminez D, Allmaras R R, Hugins E A, et al. Prediction of the saturated hydraulic conductivity-porosity dependence using fractals[J]. Soil Science Society of America Journal, 1997,61(5):1285-1292.

[9]Arora B, Mohanty B P, McGuire J T. Uncertainty in dual permeability model parameters for structured soils[J]. Water Resources Research, 2012,48(1):1-35.

[10]Allaire S E, Gupta S C, Moncrief J F. Water and solute movement in soil as influenced by macropore characteristics (1): Macropore contituity[J]. Journal of Contaminant Hydrology, 2000,41(3/4):283-301.

[11]Allaire S, Gupta S, Nieber J,et al. Role of macropore continuity and tortuosity on solute transport in soils (2): Interactions with model assumptions for macropore description[J]. Journal of Contaminant Hydrology, 2002, 58(3):283-298.

[12]Olesen T, Rolston D, Schjonning P, et al. Tortuosity, diffusivity, and permeability in the soil liquid and gaseous phases[J]. Soil Science Society of America Journal, 2001, 65(3):613-623.

[13]Olesen T, Rolston D, Schjonning P, et al. Tortuosity, diffusivity, and permeability in the soil liquid and gaseous phases[J]. Soil Science Society of America Journal, 2001,65(3):613-623.

Effect of Macropore Tortuosity on Soil Infiltration

ZHANG Shaoni1， XU Xuexuan1,2， GAO Zhaoxia2， YU Miaozi3， ZHAO Chuanpu2

(1.InstituteofSoilandWaterConservation,NorthwestA&FUniversity,Yangling,Shaanxi712100,China; 2.InstituteofSoilandWaterConservation,ChineseAcademyofSciencesandMinistryofWaterResources,Yangling,Shaanxi712100,China; 3.CollegeofNaturalResourcesandEnvironment,NorthwestA&FUniversity,Yangling,Shaanxi712100,China)

Abstract：[Objective] The effect of macropore tortuosity on infiltrition was examined in order to provide theoretical basis for how tortuosity influenced preferential flow transport. [Methods] The laboratory soil column infiltration experiments were conducted with man-made macropore in Heilu soils under different initial tortuosity. The effects of macropore tortuosity on wetting front migration, cumulative infiltration and penetration time were determined. [Results] The macropore tortuosity considerably influenced the shape of the wetting front migration and its movement in vertical and lateral directions; the decrease of macropore tortuosity could accelerate the migration of wetting front and increase the cumulative infiltration; the time for water to penetrate the soil column increased with the rise of macropore tortuosity; the depth of wetting front migration and the amount of cumulative infiltration had the exponential relationship with time. The parameters in these functions depended on the macropore tortuosity. The relationship between penetration time and macropore tortuosity could be described by a logarithmic function. [Conclusion] The macropore tortuosity extensively impacted some factors of infiltrition, and was one of the most important factors in studying preferential flow.

Keywords:macropore tortuosity; wetting front; cumulative infiltration; breakthrough time

文献标识码：A

文章编号：1000-288X(2015)04-0024-05

中图分类号：S152.7

通信作者：徐学选(1966—),男(汉族),陕西省大荔县人，博士,研究员,主要从事生态水文研究。E-mail:xuxuexuan@nwsuaf.edu.cn。

收稿日期：2014-05-03修回日期：2014-05-28

资助项目：国家自然科学基金项目“黄土丘陵区小流域大气降水—土壤水—地下水转化行为机理研究”(41171421)

第一作者：张少妮(1989—),女(汉族),硕士研究生,主要研究方向为流域管理。E-mail:zhshn1029@126.com。