一个包含Smarandache Ceil函数的对偶函数的方程

高　丽，马娅锋（延安大学　数学与计算机科学学院，陕西　延安　716000）

一个包含Smarandache Ceil函数的对偶函数的方程

高丽，马娅锋
（延安大学数学与计算机科学学院，陕西延安716000）

摘要：利用初等方法研究了一个包含Smarandache Ceil函数的对偶函数，给出了当k =6时方程的具体正整数解。

关键词：函数；对偶函数；正整数解

0　引言

著名的Smarandache Ceil函数［1-3］及其对偶函数的定义如下：

定义11［4］对任意的正整数n，k阶Smarandache Ceil函数为

定义22［4］对任意的正整数n，k阶Smarandache Ceil函数的对偶函数为

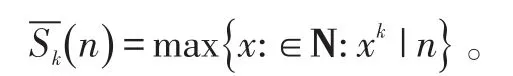
其中N是正整数集。

关于Smarandache Ceil函数的研究许多学者给出了一系列重要的结论。呼家源等在文献［5］中研究了一个包含Smarandache Ceil函数Sk(n)对偶函数及欧拉函数的方程Sk(n) =ϕ(n)的正整数解，并给出了具体解；苟素在文献［6］中研究了方程Sk(1) +Sk(2) +…+Sk(n) =Sk(1+2+…+n)有解当且仅当n=1，2，3；朱敏慧在文献［7］中研究了方程S2(n) =ϕ(n)；冯强等在文献［8］中研究了k阶Smarandache Ceil函数及其对偶函数均值的性质；赵杏花等在文献［9］中研究了方程Sk(n) + Zw(n) = 2n和Z(n) = S2(n)的可解性，并给出了它们所有解的具体形式；赵娜娜在文献［10］中研究了Smarandache Cei函数对偶函数的方程的正整数解。

在前人的研究基础上本文研究了一个包含Smarandache Ceil函数的对偶函数S() n和素因子函数Ω(n)的方程

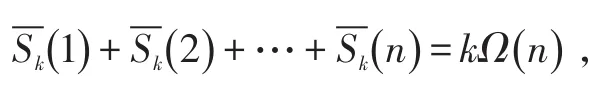
1　引理及证明

引理对任意正整数n≥64，有不等式

成立，其中

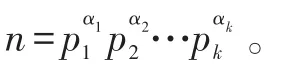
2　定理及证明

定理对任意正整数n，包含6阶Smarandache Ceil函数方程的

有解当且仅当n=18，24。

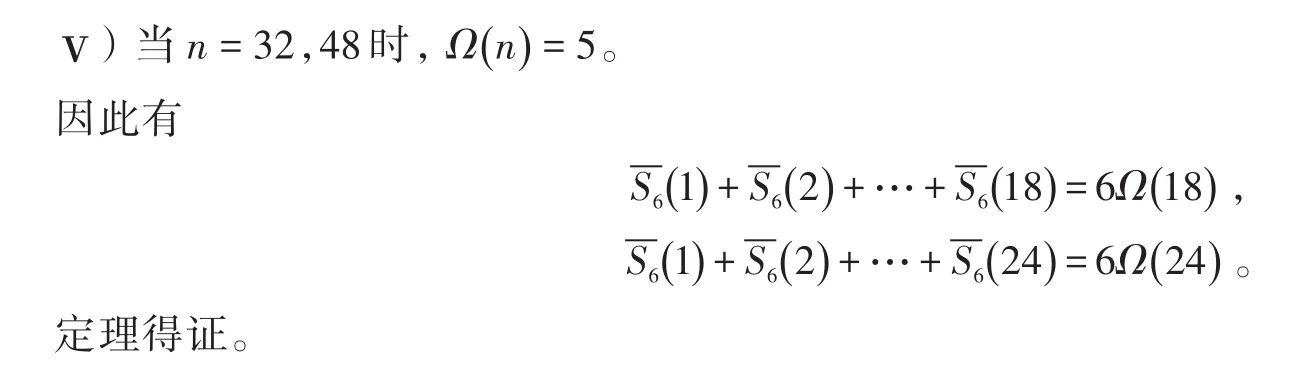
参考文献（References）

［1］潘承洞，潘承彪.初等数论［M］.北京：北京大学出版社，1992.

［2］张文鹏.初等数论［M］.西安：陕西师范大学出版社，2007.

［3］SMARANDACHE F.Olny problems，not solutions［M］.Chicago：Xiquan Publishing House，1993.

［4］马金萍.数论函数和数列的性质研究［M］.北京：科学出版社，2012：14-15.

［5］呼家源，秦伟.一个包含Smarandache Ceil函数的对偶函数及Euler函数的方程及其可解性［J］.西北大学学报：自然科学版，2013，43（3）：364-366.

［6］苟素.关于Smarandache Ceil函数的一个方程［J］.纯粹数学与应用数学，2006，22（1）：48-50.

［7］朱敏慧.一个包含Euler函数及k阶Smarandache Ceil函数的方程及其正整数解［J］.纯粹数学与应用数学，2009，25 （2）：411-416.

［8］冯强，郭金宝.关于Smarandache Ceil函数及其对偶函数的均值［J］.西南民族大学学报：自然科学版，2007，33（4）：713-717.

［9］赵杏花，郭金宝，穆秀梅，等.两个关于k阶Smarandache Ceil函数的方程［J］.陕西理工学院学报：自然科学版，2011，27（4）：74-76.

［10］赵娜娜.有关Smarandache函数方程可解性研究及均值估计［D］.西安：西北大学，2014.

（责任编辑：胡燕梅）

An Equation Involving the Smarandache Ceil Dual Function

GAO Li，MA Yafeng
（School of Mathmatics and Computer Science，Yan'an University，Yan'an 716000，Shanxi，China）

Abstract：The elementary method are usd to study the dual functioninvolving Smarandache Ceil function，all specific positive integer solution of equationare given with k=6 .

Keywords：Smarandache Ceil function Sk(n)；dual functionpositive integer solution

作者简介：高丽（1966—），女，教授，硕士，研究方向：数论和解析函数。

基金项目：国家自然科学基金资助项目（11471007）；陕西省科学技术研究发展计划项目（2013JQ1019）；延安大学校级科研计划项目（YD2014-05）

收稿日期：2015-04-09

DOI：10.16389/j.cnki.cn42-1737/n.2015.04.003

中图分类号：O156.4

文献标志码：A

文章编号：1673-0143（2015）04-0300-03