一般对称群共轭类中几个问题的初步研究

郭黎丹，胡晓莉

（江汉大学　数学与计算机科学学院，湖北　武汉　430056）

一般对称群共轭类中几个问题的初步研究

郭黎丹，胡晓莉*

（江汉大学数学与计算机科学学院，湖北武汉430056）

摘要：证明了一般对称群的共轭类完全由n的着色划分来确定的结论，并计算了一般对称群中每个共轭类所含元素的个数。

关键词：一般对称群；共轭类；划分；划分函数

0　引言

对称群在群论中占据极为重要的地位，它是表示理论的重要研究领域之一。由Cayley定理可知，每个有限群都同构于某个对称群的子群。因此，把对称群及其他子群的结构问题研究清楚，则所有有限群的结构也随之解决。另外，对称群对物理和化学上的研究都发挥着重要的作用。其晶体学上的很多问题都是通过对称群及其子群来研究的。随着研究的进一步深入，往往需要考虑更一般的对称群，通常所用到的一般对称群就是用一个有限群去半直积上对称群。早在1995年，MACDONALD［1］给出了一般对称群特征标表的计算。

群的元素可以被分割成若干不相交的共轭类的并，因为同一个共轭类上的元素具有很多共同的属性，并且从群的共轭类可以看出很多关于它们结构上的重要特征。因此研究一般对称群的共轭类具有非常重要的现实意义。我们已经知道对称群的共轭类完全由n的划分来确定，而本文把这一结论推广到了一般对称群上，详细地给出了一般对称群的共轭类与n的着色划分之间存在一一对应关系。

1　预备知识

定义11［2-3］从集合{1, 2,…, n }到集合{1, 2,…, n }的一个双射被称为一个n阶置换。所有n阶置换构成的集合是一个群，被称为n阶对称群，记为Sn。

定义2［2］由一些非负整数构成的一个非递增序列λ=（λ1,λ2,…,λl），若其中只含有限个零，则称λ为一个划分。若λ1+λ2+…+λl=n，则称λ是n的一个划分。有时候也表示成，其中mi为非负整数，表示划分λ中有mi个部分等于i。l (λ)= l称为λ的长度，|λ|=λ1+λ2+…+λl称为划分λ的权。

定义33［2］任意给定对称群Sn中的两个元素σ和τ，若存在Sn中的一个元素π，使得τ=πσπ-1，则称σ与τ是共轭的。

共轭给出了对称群Sn中元素的一个等价关系，从而给出了Sn中元素的一个分类。由共轭关系所确定的Sn的一个等价类叫做Sn的一个共轭类。

引理11［4］（Ⅰ）对称群Sn中的两个元素是共轭的当且仅当它们具有相同的型，即对称群的共轭类与n的划分一一对应。

2　一般对称群的共轭类

设Γ为有限群，Γn=Γ×Γ×…×Γ为Γ的n次直积。对称群Sn在Γn上的作用定义为：

定义4［1］设Γ为有限群，则Γn与对称群Sn的半直积被称为一般对称群，记为Γn=Γ～Sn，也称为Γ 与Sn的圈积（wreath product）。

一般对称群Γn的元素形式为( g,σ)，其中g =( g1, g2,…, gn)，gi∈Γ，σ∈Sn。任意给定( g,σ)，( h,τ)∈Γn，其乘法定义为( g,σ)·( h,τ)=( g∙τ( h)，στ)。特别地，当Γ=1时，Γn就是对称群Sn。易知，|Γn|=|Γn|∙|Sn|=|Γ|nn!。

设Γ*=( c1, c2,…, cr)为有限群Γ的所有不等价的共轭类构成的集合。任意给定( g,σ)∈Γn( g = ( g1, g2,…, gn)，gi∈Γ，σ∈Sn)，把σ写成不相交的循环置换的乘积形式：σ=σ1σ2…。设σi=则有落在Γ的哪个共轭类里完全由g与σi来决定，由此它被叫做( g,σ)对应于循环置换σi的循环积。设c∈Γ*，令mk(c)表示σ中循环长度为k并且其循环积落在共轭类c中循环置换的个数，那么令则ρ( c)为被共轭类c着色了的划分，从而是被Γ的共轭类集Γ*着色的一个着色划分，并且权为n。由( g,σ)和Γ*确定的着色划分被叫做元素( g,σ)的型。

例如：Γ=a|a6=1为一个6阶循环群，则Γ*={ 1, a, a2, a3, a4, a5}，Γ6=Γ6～S6。考虑( g,σ)∈Γ6，其中g =( a4, 1, a2, a5, a3, a)，σ=σ1σ2σ3=（531）（62）（4），那么有

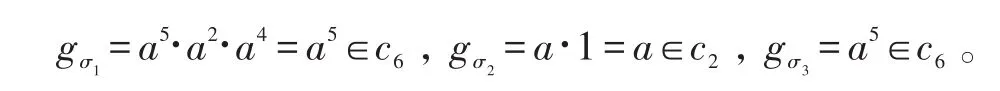
从而，由( g,σ)和Γ*确定的着色划分为ρ=( ( 2)c2, ( 31)c6)。

定理11一般对称群Γn中的两个元素是共轭的当且仅当它们具有相同的型，即Γn的共轭类与被Γ*着色的n的着色划分有着一一对应关系。

定理22 Γn中型为的共轭类所含元素个数为

参考文献（References）

［1］MACDONALD I G.Symmetric functions and hall polynomials［M］.New York：Oxford University Press，1995：169-171.

［2］SAGAN B E.The symmetric group［M］.2nd ed.New York：Springer，1998：1-3.

［3］HU X L，JING N H.Spin characters of generalized symmetric group［J］.Monatshefte für Mathematik，2014，173（4）：495-518.

［4］胡晓莉.圈积群的投射特征［D］.广州：华南理工大学，2012.

（责任编辑：胡燕梅）

Discussion on Some Problems of Conjugacy Classes of Generalized Symmetric Group

GUO Lidan，HU Xiaoli*
（School of Mathematics and Computer Science，Jianghan University，Wuhan 430056，Hubei，China）

Abstract：It is proved that the conjugacy classes of generalized symmetric group are determined by the colored partitions of n，then calculates the cardinality of each conjugacy class.

Keywords：generalized symmetric group；conjugacy class；partition；colored partition function

*通讯作者：胡晓莉（1984—），女，讲师，博士，研究方向：代数。E-mail：xiaolihumath@163.com

作者简介：郭黎丹（1994—），女，研究方向：数学与应用数学。

基金项目：国家数学天元基金项目（11426116）

收稿日期：2015-04-21

DOI：10.16389/j.cnki.cn42-1737/n.2015.04.002

中图分类号：O152.1

文献标志码：A

文章编号：1673-0143（2015）04-0297-03