大规模风电场次同步振荡分析

2015-03-14顾威徐梅梅邵梦桥陈婧华徐振宇张旭王莹莹

电力建设 2015年4期

顾威，徐梅梅，邵梦桥，陈婧华，徐振宇，张旭，王莹莹

(1. 贵州电力试验研究院，贵阳市 550002；2.华北电力大学，北京市 102206；3. 北京四方继保自动化股份有限公司，北京市 100084)

(1. Guizhou Electric Power Test and Research Institute, Guiyang 550002, China; 2. North China ElectricPower University, Beijing 102206, China;3.Beijing Sifang Automation CO., Ltd., Beijing 100084, China)

大规模风电场次同步振荡分析

顾威1，徐梅梅1，邵梦桥1，陈婧华2，徐振宇2，张旭2，王莹莹3

(1. 贵州电力试验研究院，贵阳市 550002；2.华北电力大学，北京市 102206；3. 北京四方继保自动化股份有限公司，北京市 100084)

对基于双馈异步发动机(doubly-fed induction generator，DFIG)的大规模风电场经串补送电进行了次同步振荡的分析，所建立模型基于IEEE第一标准模型。在建立风电场详细数学模型的基础上进行了小干扰稳定性分析，并在电力系统分析软件 DIgSILENT/Power Factory 中建立电力系统模型，采用时域仿真验证小干扰特征值分析的结果，验证了引起风电场次同步振荡的原因是感应发电机效应而不是扭转相互作用。同时分析了控制器参数对次同步振荡特性的影响。

次同步谐振(SSR)；双馈异步发电机(DFIG)；小信号分析；感应发电机效应(IGE)；扭转相互作用 (TI)

0 引言

串联补偿电容作为一种技术较为成熟且最为经济的输电方式被多数大规模风电功率外送所采用。但交流线路加串联电容补偿的输电方式，可能会引起发电机组的次同步谐振(subsynchronous resonance, SSR)问题，成为电网安全的一大威胁。

对于风电系统中采用串联电容补偿带来的次同步谐振的实例，目前仅有2009年秋天美国德州电力可靠性委员会系统中发生的一起由于近电气侧发生交流故障引起的含串补电容风电场次同步谐振现象[1]。

文献[1-4]建立了用于次同步振荡特征值分析的双馈异步风电机组模型，讨论了特征值分析的4个模态，并对风电并网的次同步振荡的影响因素进行了分析，通过时域仿真来验证其结果。研究发现：风速越低，串补度越高，双馈感应型风电机组次同步谐振越严重。

风电场经串补并网除了可能会发生SSR，风电机组控制器与外部控制器耦合也会引发次同步振荡，此类次同步振荡的频率和衰减率由风电控制器参数和输电系统参数共同决定，与轴系固有模态频率完全无关，且比次同步谐振SSR发散得更快。

文献[6]采用基于阻抗的Nyquist稳定判据来分析风电场并网SSR，指出电气系统与风电场控制器之间的相互作用是引发SSR的主要原因。

文献[7-8]分析了次同步控制相互作用(sub-synchronous control interaction，SSCI)发生的原因，并设计了一个附加阻尼控制器来抑制SSCI，取得了良好的抑制效果。目前对SSCI的研究较少，其产生机理还不十分明确，对其抑制措施的研究也较欠缺。

本文针对基于双馈异步发动机(doubly-fed induction generator， DFIG)的大规模风电场经串补送电进行次同步振荡的分析，第2部分主要介绍串联补偿引起的次同步谐振的基本理论，第3部分建立适合于研究次同步振荡的详细的系统数学模型，主要包括：轴系模型、感应发电机模型、转子侧变换器(rotor side converter，RSC)模型、网侧变换器(grid side converter,GSC)模型、直流环节电容模型、线路和串补模型。第4部分在建立的数学模型的基础上进行小干扰稳定分析，求解状态方程，得到特征值来判断系统稳定性。第5部分在电力系统分析软件 DIgSILENT/Power Factory 中建立电力系统模型，采用时域仿真验证特征值分析的结果。第6部分得出结论。

1 次同步谐振(SSR)基本理论

具有串联电容补偿的系统网络，其自然谐振频率为

(1)

式中f0为同步频率，Hz。

在次同步频率为fn时，对应的转差率s1为

(2)

式中fm为对应于转子转速的电气频率，此时由于fn要小于fm，则s1<0。稳态时，由感应电机的等效电路可知，在这个次同步频率fn下的等效转子电阻为负的，当这一负值电阻超过此频率下的电枢电阻与网络电阻之和时，系统的总电阻在此次同步频率下为负值，就会导致电枢绕组中的次同步频率电流持续存在，甚至会增大，这种现象就是所谓的感应发电机效应(inductiongeneratoreffect，IGE)。

而扭转相互作用(torsionalinteraction，TI)主要是指电力系统中的机械系统与串联电容补偿系统网络间的相互作用，这种相互作用与机械系统和电气系统的动态特性均有关。假设发电机转子的轴系自然扭振频率为fe，转子在这一频率下的振荡在电机的电枢绕组上感应出频率为fen=f0-fe和fen=f0+fe的电压分量。当电枢绕组上感应的次同步电压分量的频率与电气系统的某一自然谐振频率相接近时，电枢绕组上次同步电压分量所产生的次同步电流又会在转子上产生与转子持续振荡同步的转矩，若这种与转子相对于同步速差同相位的次同步转矩分量等于或大于旋转系统在该品类别下的固有阻尼转矩，系统就会被“自激”[9]。电气系统与机械系统间的这种相互激励作用就叫做扭转相互作用(TI)。

2 系统模型

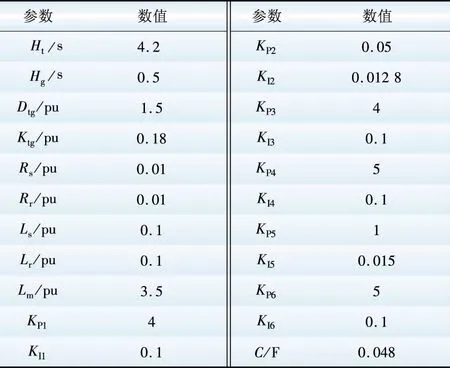
本文所采用的系统模型是基于IEEE第一标准模型演变而来，如图1所示。该大型风电场装配有100台2MW的双馈感应异步风力发电机，风电机组通过0.69/35kV变压器接入风电场内部电网，并通过35/525kV变压器升压后经一串补线路送入外部系统。风力机及其控制参数如表1所示。文献[10]提出当风电机组差别不大时，在分析整个风电机群的动态行为时可采用单机的等值模型，同时采用单机等值模型对风电场次同步振荡进行分析。同样文献[2]分析SSR时对一个大规模风电场也采用单机DFIG等值模型表示。文献[11-12]也提出采用单机等值模型分析系统动态是合理的。文献[13]提出采用单机等值模型对风电场进行动态仿真不仅减小了对大量风机建模的工作量，而且采用等值模型与采用详细模型仿真结论相似。文献[3]提出当风电场风电机组增加或减少时，其功率基准值也会相应增加或减少，因此单位惯性常数H不变。同样，这也适用于风机的其他参数。

本研究系统模型包括：轴系模型、感应发电机模型、转子侧变换器模型、网侧变换器模型、直流环节电容模型、线路和串补模型。

2.1 轴系模型

风力机的轴系分为高速轴、低速轴和齿轮箱，由于齿轮箱的质量很小可忽略不计，因此轴系模型采用双质量块模型[14-15]。转子轴系采用双质量块模型，其状态方程为

(3)

式中：Ht代表风轮机的惯性常数；Hg代表发电机的惯性常数；ωt代表风轮机的转速；ωg代表发电机的转速；θtg为轴的扭转角度；Tm、Te分别为风轮机的机械转矩和发电机的电磁转矩，其中Te按电动机方式定义；Dt、Dg分别代表风轮机的阻尼系数和发电机的阻尼系数，Dtg代表轴系的阻尼系数；Ktg代表轴系的刚度系数。

2.2 感应发电机模型

图2为双馈感应发电机d、q坐标系下的等效电路图。

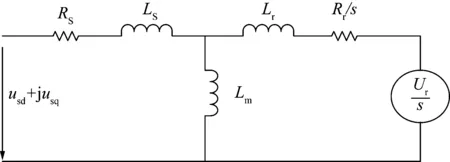
图2 双馈感应发电机d、q坐标系下的等效电路图

根据定、转子电压和磁链方程推导得到一个四阶动态模型，其状态方程为[16]

(4)

(5)

(6)

(7)

其中：

(8)

(9)

(10)

(11)

(12)

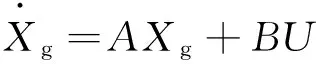
2.3 转子侧和网侧变换器模型

转子侧变换器采用定子磁链定向的控制策略来实现有功和无功功率的解耦，其控制框图如图3所示。网侧变换器采用基于电网电压定向的控制策略，其控制框图如图4所示。

图3 转子侧变换器控制框图

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

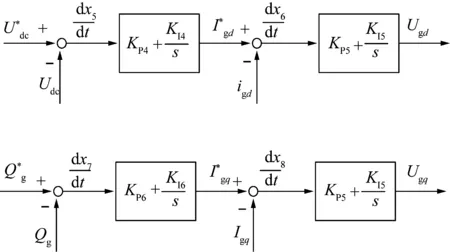
图4 网侧变换器控制框图

图4中KP4、KI4分别为电网侧变换器直流电压控制环节的比例和积分增益，KP6、KI6分别为电网侧变换器无功控制环节比例和积分增益，KP5、KI5分别为电网侧变换器电流控制环节比例和积分增益，引入中间变量x5、x6、x7、x8，网侧变换器状态方程为

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

2.4 直流环节电容模型

直流环节电容采用一阶动态模型，其状态方程为[17]

(29)

式中：Udc为直流电容电压，Pr、Pg分别为转子侧与电网侧的有功功率。

2.5 线路和串补模型

线路和串补在d、q坐标轴下状态方程为[2]

(30)

式中，Ucd、Ucq分别为电容两端d、q参考坐标下电压；Id、Iq分别为d、q轴输电线路电流；Ed、Eq分别为无穷大母线电压；Utd、Utq分别为发电机机端d、q参考坐标下电压；XL∑=XL+XT1+XT2。

3 特征值分析

小干扰特征值分析广泛应用于电力系统稳定性分析中，包括低频振荡分析和SSR分析。它是在小干扰的背景下，对系统进行线性化，通过对状态方程的系数矩阵特征值的求取，来判定系统稳定性。

对系统在某一稳定运行点进行线性化，得到全系统的状态方程与输出方程，可表示为：

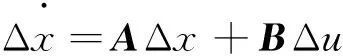
(31)

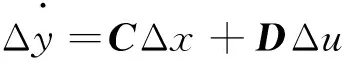
(32)

若矩阵A的所有特征值具有负的实部，则系统在该运行点是小干扰稳定的；若矩阵A有一个或多个实部为正的特征根，则系统在此运行工况下是不稳定的。

本文形成的全系统的线性状态方程包括：输电线路网络和串联补偿电容线性状态方程组，双馈感应发电机轴系线性状态方程组，感应发电机和控制器状态方程组，所有方程组综合起来描述了当采用容量固定电容补偿时，单机无穷大双馈机组风电系统的所有动态行为。综合上一节的分析，形成20阶状态方程。

3.1 串补度影响分析

分析SSR现象主要分析扭转相互作用和异步发电机效应，因此做特征值分析可以进行选择模态分析，找出所关心的特征值。改变轴系的固有参数，λ1,2发生较大改变，其他模式几乎不受影响，判断该模式为扭振模式；串补度改变时，λ3,4发生相应改变，且通过对线路的自然振荡频率fn进行估算，发现该模式下的振荡频率与系统的自然振荡频率接近互补，因此该模式为电网模式[2]。

表2为不同串补度扭振模式和电网模式值。

表2 不同串补度扭振模式和电网模式值

Table 2 Torsional mode and network mode at various series compensation levels

分析扭振模式，串补度对扭振模式几乎没有影响，扭振模式是由轴系的固有特性决定的。

分析电网模式，随着串补度的增加，该模式的振荡频率减小，同时，由于感应发电机效应，其阻尼也随之减小。

为了更直观地分析电网模式阻尼特性和振荡频率与串补度的关系，现做模态阻尼-串补度、振荡频率-串补度曲线如图5和6所示。

从图5可以看出，随着串联补偿度的增加，模态阻尼向正值移动，即阻尼下降，且串补度高于50%时阻尼为正值，即呈现不稳定增幅振荡。

从图6可以看出，随着串联补偿度增加，振荡频率随之降低，这是由于当串联补偿度上升时，电网自然振荡频率增加，则其互补频率降低的缘故。

图5 不同串补度下的电网模式模态阻尼曲线

图6 不同串补度下的电网模式振荡频率曲线

3.2 风电场PI控制参数影响分析

次同步控制相互作用是指由双馈风力发电机控制器引起的次同步振荡。当线路电流，即 DFIG定子电流存在次同步频率的振荡分量时，RSC 采集的瞬时功率及瞬时电流ir都会发生变化，经RSC控制，会导致逆变器输出电压，即双馈风力发电机的转子电压Ur变化，Ur的变化会反作用于转子电流Ir，同时感应定子电流变化，产生新的次同步电流。风电控制引起次同步振荡过程示意如图 7 所示[18]。

图7 风电控制引起次同步振荡过程示意图

新的次同步电流与原始扰动电流量叠加，若两者相位差小于90°，则原始扰动电流被助增，该频率下的次同步电流由于形成正反馈而逐渐增大，即双馈风力发电机转子侧变频器的控制与串补线路形成相互激励，进而导致其输出的有功和无功功率振荡发散。目前，RSC 通常采用双闭环比例积分(proportional integral，PI)调节的矢量控制策略，功率外环的动态响应时间长，电流内环的响应速度快，可以快速追踪电流参考值，因此 SSCI 受 RSC 电流内环控制参数的影响较大[18]。因此，本文重点讨论内环参数的影响。

考虑转子侧变频器电流环控制参数对次同步振荡的影响，线路上加50%的串补，同样，系统受扰后，线路上的谐振频率fer=23.34 Hz，当电流内环控制积分系数KI保持不变，取KI=0.012 8，比例系数Kp分别取不同的值时，计算特征值如表3所示(仅列出电网模式)。其中，Kp=0.05的值对应表2中50%串补度电网模式值。

表3 不同PI参数下电网模式值

Table 3 Network mode values with various PI parameters

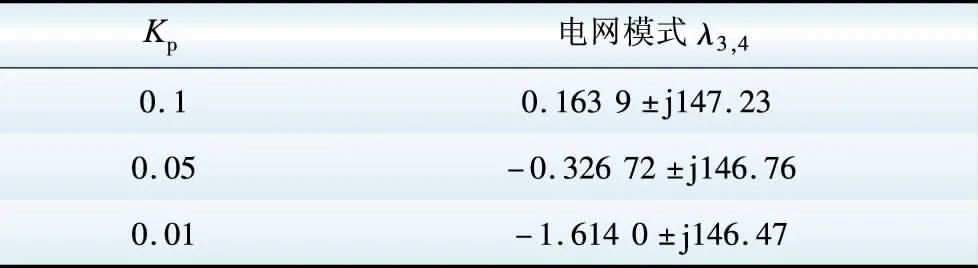
由表3可以看出，保持KI不变，当Kp取值逐渐增大时，电网模式逐渐趋于不稳定；当Kp=0.1时，阻尼为正，即呈现不稳定增幅振荡。

4 时域仿真验证

4.1 感应发电机效应(IGE)

在电力系统分析软件DIgSILENT/PowerFactory中建立电力系统模型，所建立系统模型如图1所示。在bus3处t=1 s时设置3项故障，t=1.1 s切除故障，在不同串联补偿度下，采用时域仿真验证特征值分析的结果。

图8为线路40%串联补偿度下的时域仿真结果，在该串补度下，扰动后风电场输出有功功率和电磁转矩在振荡后趋于稳定，对电磁转矩做快速傅里叶变换分析发现，该工况下电磁转矩次同步分量(26 Hz，163.28 rad/s)，接近表2在40%串补度下电网模式特征值的分析结果164.300 65 rad/s。

图9为线路在60%串联补偿度下的时域仿真结果。在该串补度下，扰动后风电场输出有功功率和电磁转矩呈现不稳定增幅振荡，对电磁转矩做快速傅里叶变换分析发现，该工况下电磁转矩次同步分量(21 Hz，131.88 rad/s)，接近表2在60%串补度下电网模式特征值的分析结果130.001 67 rad/s。

图8 40%串补度下时域仿真结果

图10为线路在80%串联补偿度下的时域仿真结果，在该串补度下，扰动后风电场输出有功功率和电磁转矩呈现不稳定增幅振荡，对电磁转矩做快速傅里叶变换分析发现，该工况下电磁转矩次同步分量(17 Hz，106.76 rad/s)接近表2在80%串补度下的电网模式特征值分析结果105.203 02 rad/s。

4.2 扭转相互作用(TI)

对于双质量块的发电机轴系，其自然振荡频率为

(33)

图9 60%串补度下时域仿真结果

现代风电机组惯性系数和轴系刚度的典型值如表4所示[15]。

根据式(33)计算得出最大自然振荡频率不超过5 Hz，即使在较高的补偿度下，串补电路的自然振荡频率也不可能达到45 Hz,因此在典型的风机轴系参数值下，不大可能发生轴系扭转相互作用。从不同串补度下的扭振模式也可以看出该点，串补度对扭振模式几乎没有影响，扭振模式是由轴系的固有特性决定的。

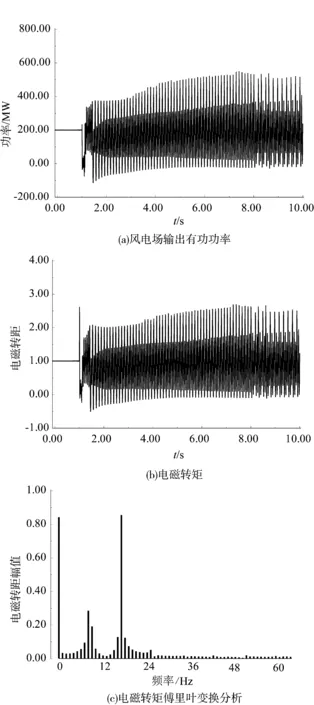
图10 80%串补度下时域仿真结果

为了进一步验证电气系统与机械系统之间是否存在扭转相互作用，设在bus3处t=1 s时设置3项故障，t=1.1 s切除故障，分别观察不同串补度下的轴系2个质量块之间的扭矩，其仿真结果如图11所示。

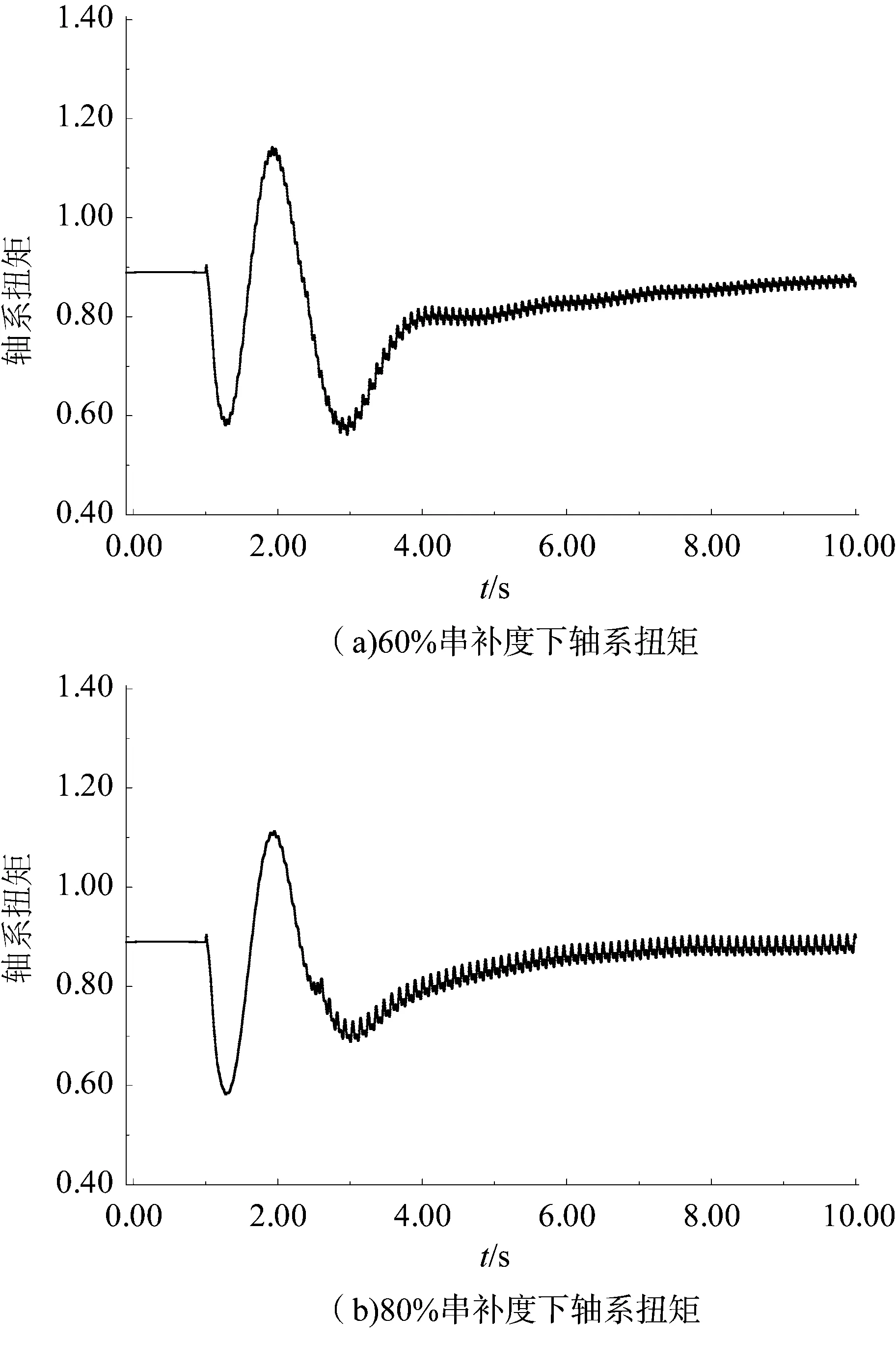
图11 不同串补度下的轴系两质量块之间扭矩

虽然在60%和80%串补度下均已明显发生自励磁现象，其有功功率和电磁转矩均出现不稳定增幅振荡，但轴系扭矩并没有发散，这说明电气系统与机械系统间并未发生不稳定的扭转相互作用。引起风电场次同步振荡的主要原因是感应发电机效应，而不是扭转相互作用。

4.3 次同步控制相互作用(SSCI)

图12为50%串补度下在不同内环控制参数下的输出功率仿真图。

5 结论

本文对基于DFIG的大规模风电场经串补送电进行了次同步振荡的分析，分析方法包括特征值分析，并用时域仿真验证结果。由于风机的固有参数，决定了其轴系的自然振荡频率较低，即虽然在较高串补度下也不可能发生扭转相互作用，本文也用时域仿真证明了该点。通过特征值分析电网模式，随着串补度的增加，该模式的振荡频率减小，同时，由于感应发电机效应，其阻尼也随之减小。由于异步发电机效应，随串补度增加等效电阻随之减小，阻尼也随之减小，高于50%串补度时，发生自励磁，风电场输出功率产生不稳定增幅振荡。当双馈风力发电机转子侧电流内环PI控制的比例系数增大时，次同步电流趋于发散，即发生SSCI。

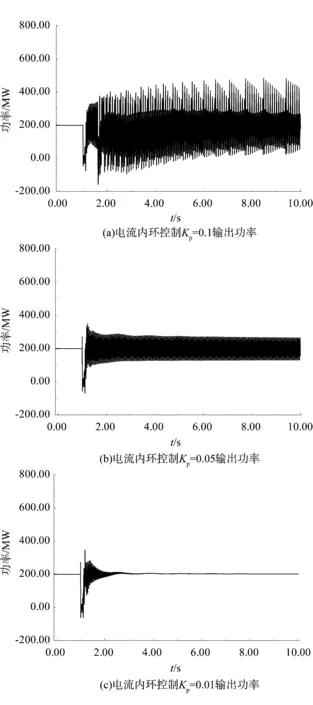
图12 不同内环控制参数下时域仿真结果

[1]Fan L L, Zhu C X, Miao Z X, et al. Modal analysis of a DFIG-based wind farm interfaced with a series compensated network[J]. IEEE Transactions on Energy Conversion, 2011, 26(4): 1010-1020.

[2]Fan L L, Kavasseri R, Miao Z X, et al. Modeling of DFIG-based wind farms for SSR analysis[J]. IEEE Transaction on Power Delivery, 2010, 25(4): 2073-2082.

[3]Fan L L, Miao Z X. Modeling and simulation of a DFIG-based wind turbine for SSR[J]. IEEE Transactions on Energy Conversion, 2011, 26(4):1010-1020.

[4]Zhu C X, Fan L L, Hu M Q. Modeling and simulation of a DFIG-based wind-power system for stability analysis[C]//2012 IEEE Power and Energy Society General Meeting, San Diego, 2012.

[5]John A, Venkata A P, Anuj D. ERCOT experience screening for sub-synchronous control interaction in the vicinity of series capacitor banks[C]//Power and Energy Society General Meeting, San Diego, 2012.

[6]Fan L L, Kavasseri R, Miao Z X, et al. Impedance-model-based SSR analysis for type 3 wind generator and series-compensated network[J]. IEEE Transactions on Power Delivery, 2010,25(4):2073-2082.

[7]Garth D I, Amit K J, Andrew L I, et al. Sub-synchronous control interactions between type 3 wind turbines and series compensated AC transmission systems[C]//2011 IEEE Power and Energy Society General Meeting, San Diego, 2011.

[8]Badrzadeh B, Sahni M, Muthumuni D, et al. Sub-synchronous interaction in wind power plants(part I:study tools and techniques[C]//2012 IEEE Power and Energy Society General Meeting, San Diego, 2012.

[9]程时杰,曹一家,江全元.电力系统次同步振荡的理论与方法[M].北京:科学出版社,2009.

[10]Fan L L, Miao Z X. Mitigating SSR using DFIG-based wind generation[J]. IEEE Transactions on sustainable energy, 2012, 3(3):349-358.

[11]Piwko R, Miller N, Sanchez-Gasca J, et al. Integrating large wind farms into weak power grids with long transmission lines[C]//IPEMC 2006: CES/IEEE 5th International Power Electronics and Motion Control Conference, Shanghai, 2006.

[12]Miller N W, Price W W, Sanchez-Gasca J J. Dynamic modeling of GE 1.5 and 3.6 wind turbine-generators[C]// 2003 IEEE Power Engineering Society General Meeting, Toronto, 2003.

[13]Slootweg J G, Kling W L. Aggregated modelling of wind parks in power system dynamics simulations[C]// 2003 IEEE Bologna PowerTech Conference, Bologna, 2003.

[14]王波.含双馈机组风电场次同步振荡分析与抑制[D].重庆:重庆大学,2013. Wang Bo. Analysis and suppression of subsynchronous oscillation in wind farm with doubly fed wind induction [D].Chongqing: Chongqing University, 2013.

[15]Muyeen S M, Ali M H, Takahashi R, et al. Comparative study on transient stability analysis of wind turbine generator system using different drive train models[J]. Renewable Power Generation, IET, 2007, 1(2):131-141.

[16]关宏亮.大规模风电场接入电力系统的小干扰稳定性研究[D].北京:华北电力大学，2008.

[17]Ghofrani M, Arabali A, Etezadi-Amoli M. Modeling, analysis, and suppression of the impact of full-scale wind-power converters on subsynchronous damping[C]// 2012 IEEE Power and Energy Society General Meeting, San Diego, 2012.

[18]栗然，卢云，刘会兰，等.双馈风电场经串补并网引起次同步振荡机理分析[J]. 电网技术,2013,37(11):3073-3079. Mechanism analysis on subsynchronous oscillation caused by grid-integrations of doubly Fed wind power generation system via series compensation[J]. Power System Technology, 2013, 37(11): 3073-3079.

(编辑:刘文莹)

Subsynchronous Resonance of Large-Scale Wind Farms

GU Wei1, XU Meimei1, SHAO Mengqiao1, CHEN Jinghua2,XU Zhenyu2, ZHANG Xu2, WANG Yingying3

This paper analyzes the subsynchronous resonance (SSR) phenomena in DFIG-based (doubly-fed induction generator) wind farms interconnected with series compensated networks. The study system was derived from IEEE first benchmark model. Small-signal stability analysis was conducted on the basis of detailed mathematical model of wind farm. The model of power system was constructed by power system analysis software DIgSILENT/Power Factory, and time domain simulations were performed to confirm the results of small-signal eigenvalue analysis. The results show that IGE (induction generator effect) instead of TI (torsional interaction) is the major reason for SSR in such systems. Finally, this paper analyzes the influence of controller parameters on the characteristics of SSR.

subsynchronous resonance (SSR)； doubly-fed induction generator (DFIG)； small-signal analysis； induction generator effect (IGE)； torsional interaction (TI)

Xs=ωsLs

Ugd=KP5(KP4ΔUdc+KI4x5-Igd)+KI5x6

Ugq=KP5(KP6ΔQg+KI6x7-Igq)+KI5x8

TM 614

1000-7229(2015)04-0095-09

10.3969/j.issn.1000-7229.2015.04.016

2014-10-20

2015-01-27

顾威(1986)，女，工程师，硕士，研究方向为风力发电；

徐梅梅(1986)，女，工程师，硕士，研究方向为电力系统计算分析；

邵梦桥(1973)，男，高级工程师，研究方向为电力系统分析；

陈婧华(1989)，女，硕士研究生，研究方向为电力系统保护与控制；