一类有时变时延耦合动态节点的复杂网络同步

巩长忠，石海云

（中国民航大学理学院，天津 300300）

一类有时变时延耦合动态节点的复杂网络同步

巩长忠，石海云

（中国民航大学理学院，天津 300300）

针对一类具有时变时延动态节点的复杂网络,研究其同步问题。基于Lyapunov稳定性理论和线性反馈控制理论,设计了线性控制器,得到具有时变时延耦合动态节点的复杂网络同步的充分条件。最后,利用数值仿真验证了方法的有效性。

同步;复杂网络;耦合;时变时延;节点

现实生活中，复杂网络无处不在，复杂网络的同步问题更是引起各个领域的广泛关注。文献[1]中研究了无时延的有不同节点的网络同步问题，文献[2]中研究了有时延的不同节点间的网络同步问题，文献[3]在文献[1-2]的基础上研究了有时延的不同节点的自适应耦合的网络同步问题。文献[4]研究了有时延动态节点耦合复杂网络的脉冲同步问题。上述研究中的时延均为定值，本文研究具有时变时延的动态节点的复杂网络的同步问题，增加了系统的复杂性。

1 预备知识

本文将分析具有时变时延和非线性内部耦合函数的复杂动态网络的同步问题，模型如下

其中：i=1，2，…，N，xi（t）=（xi1（t），xi2（t），…，xin（t））T∈Rn（i=1，2，…，N）是第i个节点的状态向量；f：R×Rn→Rn是一个光滑的非线性函数；τ1（t）是动态节点的时延函数；τ2（t）是耦合的时延函数；Γ1∈Rn×n和Γ2∈Rn×n是内耦合矩阵；A=（aij）N×N∈Rn×n和B=（bij）N×N∈Rn×n是加权配置矩阵。如果节点i和节点j（i≠j）之间有联系，则aij>0，bij>0；否则aij=bij=0。

假设1 对于向量值函数f（t，xi（t），xi（t-τ1（t）））假设存在常数θ>0，γ>0，任意的x，y∈Rn×n和t≥0使得f满足semi-Lipschitz条件

假设2 对i∈N，τi（t）是一个微分函数且0≤τ˙i（t）<ε<1。

假设3 内耦合矩阵Γ是一个正定矩阵。

引理1 对任何向量x，y∈Rn和一个正定矩阵Q∈Rn×n，矩阵不等式

成立。

2 同步分析

将模型（1）作为驱动系统，则响应系统的模型如下

其中：yi（t）=（yi1（t），yi2（t），…，yin（t））T∈RN（i=1，2，…，N）是响应系统的第i个节点的状态向量；ui是线性控制器，设计如下：ui=-diei（t）。

定义驱动系统（1）和响应系统（2）的误差为

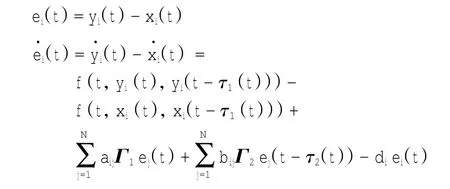
定理1 对于驱动系统（1）和响应系统（2），如果满足下面的条件

其中：ρ>0且是一个常数。Q=A⊗Γ1，P=B⊗Γ2，I∈Rn×n是单位矩阵，λmax是相应的最大特征值。那么系统（1）和（2）达到同步。

证明取Lyapunov函数为

3 数值仿真

为了证明该方法的有效性，在Matlab的环境下进行了数值仿真。节点的动力学方程为

加权配置耦合矩阵A，B有如下形式

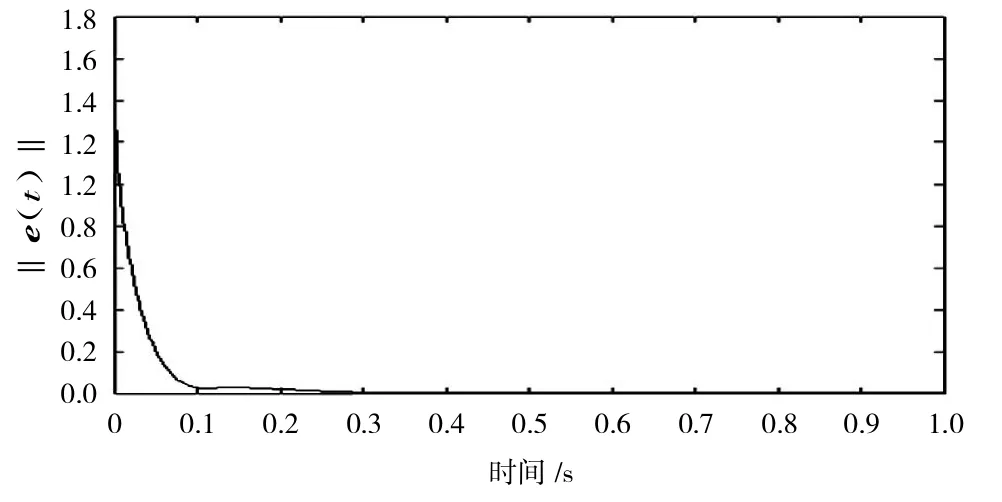
图1 同步误差‖e（t）‖Fig.1 Synchronization error‖e（t）‖

t∈[0，+∞）是同步误差的2-范数，由定理1知整个网络渐近同步。图1和图2给出仿真的部分结果，可知系统（3）和（4）的误差曲线迅速地收敛到0，即系统（1）和（2）能很好地达到同步。

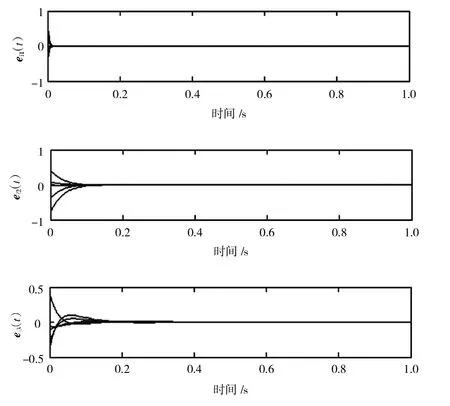
图2 同步误差ei1，ei2，ei3Fig.2 Synchronization errors ei1，ei2，ei3

4 结语

本文讨论了节点及耦合项都含有时变时延的复杂动态网络的同步问题。基于Lyapunov稳定性理论和线性控制理论，设计了线性控制器，从而给出网络间同步的充分条件。为了验证方法的有效性，进行了数值仿真。从仿真结果可以发现网络同步的速率不仅受反馈强度和时间延迟的影响，也会受到网络规模和结构的影响。数值仿真的结果检验了理论的有效性。

[1]SONGQ，CAO J，LIU F.Synchronization of complex dynamical networks with nonidentical nodes[J].Phys Lett，2010，A374：544-551.

[2]CAI S，HE Q，HAO J，et al.Exponential synchronization of complex networks withnonidentical time-delayed dynamical nodes[J].Phys Lett，2010，A374：2539-2550.

[3]HU CHENG，YU JUAN，JIANG HAIJUN，et al.Synchronization of complex networks with nonidentical nodes and adaptive coupling strength [J].Phys Lett，2011，A375：873-879.

[4]WU SHUGUO，YAO HONGXING.Impulsive synchronization of two coupled complex networks with time-delayed dynamical nodes[J].Chin Phys，2011，B20：1056-1062.

（责任编辑：杨媛媛）

Synchronization of a class of coupled complex networks with time-varying and delayed dynamical nodes

GONG Chang-zhong，SHI Hai-yun
（College of Science，CAUC，Tianjin 300300，China）

The synchronization of two coupled complex networks with time-varying and delayed dynamical nodes is studied. Based on the Lyapunov stability and the liner feedback control theory，the linear controller is designed and some corresponding sufficient synchronization conditions are derived.Finally，numerical simulations are presented to verify the effectiveness and the correctness of the synchronization criteria.

synchronization；complex network；couple；time-varying delay；node

TP273

:A

:1674-5590(2015)02-0057-03

2013-09-03；

:2013-11-21

:中央高校基本科研业务费专项（ZXH2012B003，ZXH2012K002）

巩长忠（1959—），男，山东蓬莱人，教授，博士，研究方向为非线性控制.