捷联航姿系统航行状态下的组合对准算法研究*

李 莹 杨 新 李 波

(1.92941部队95分队 葫芦岛 125001)(2.北京西三环中路19号 北京 100841)(3.天津市公安边防总队 天津 300457)



捷联航姿系统航行状态下的组合对准算法研究*

李 莹1杨 新2李 波3

(1.92941部队95分队 葫芦岛 125001)(2.北京西三环中路19号 北京 100841)(3.天津市公安边防总队 天津 300457)

由于捷联航姿设备无纬度解算值,导致跨纬度航行时航向误差过大,引入计程仪速度与航姿设备输出姿态、航向一起对纬度值进行计算,航行状态引入计程仪信息后建立数学模型进行初始对准,经航行实验验证,72小时内航向角误差得到了极大的缩小,验证了该数学模型的可行性,可提高设备的精度,具有实际使用意义。

捷联航姿; 姿态矩阵; 数学模型; 计程仪速度; 卡尔曼滤波器

Class Number U666.1

1 引言

惯性导航系统是根据测得的运载体的加速度,经过积分运算求得速度与位置的,为此,必须知道初始速度和初始位置。此外,以地理坐标系为导航坐标系的惯导系统(包括平台式和捷联式),物理平台和数学平台都是测量加速度的基准,而且平台必须准确地对准和跟踪地理坐标系,以避免由平台误差引起加速度测量误差。在惯导系统加电启动后,平台的三轴指向是任意的,可不在水平面内,又没有确定的方位,因此在系统进入导航工作状态前,必须将平台的指向对准,此过程便称为惯导系统的初始对准[1～3]。初始对准的精度直接关系到惯导系统的工作精度,初始对准的时间是惯导系统的重要战术技术指标。由于航姿设备无纬度解算值,需要引入外部位置信息或速度信息,同时,在几乎所有舰艇上均有计程仪设备,本文基于此引入计程仪速度与航姿设备输出姿态、航向一起对跨纬度值进行计算,经实际使用证明可大幅提高航姿设备的精度。

2 精对准方程的建立

对于捷联系统,由于捷联矩阵起到了平台的作用,因此导航工作一开始就需要获得捷联矩阵的初始值,显然捷联系统的初始对准就是确定捷联矩阵的初始值。捷联式的姿态矩阵实际上是运载体坐标系和地理坐标系之间的方向余弦矩阵。由于粗对准确定的姿态矩阵还有较大误差,因此实际建立的导航坐标系n′与理想导航坐标系n仍存在偏差角,即失准角φ[4～5]。精对准就是估计出失准角,对粗对准确定的姿态矩阵做一次性修正。

在组合滤波精对准中采用Kalman滤波器进行状态估计,需要建立航姿设备的对准阶段误差模型[6～7]。

采用地理坐标系作为导航坐标系时简化的误差模型为

(1)

式中:φe,φn,φu为计算导航坐标系和导航坐标系之间的失准角;δVe,δVn为载体东向和北向速度误差;Ve,Vn为载体的东向速度和北向速度;Rm,Rn为载体所在点的子午曲率半径和卯酉曲率半径;L,ωie分别为当地地理纬度和地球自转角速度;fe,fn,fu为比力在导航坐标系下的投影;εe,εn,εu为陀螺的器件误差,εx,εy,εz在导航坐标系下的投影有

在对准阶段,捷联航姿设备的误差模型中包括陀螺和加速度计的器件误差。器件误差包含三种分量:随机常值误差、一阶马尔可夫过程和白噪声误差。马尔可夫过程的相关时间一般大于1小时,所以这种误差可近似视为随机常数,且与随机常值漂移相比小1～2个数量级。所以,陀螺和加速度计误差模型可简化为

(2)

(3)

式中的状态向量和系统噪声分别为

(4)

3 航向状态下组合对准模型的建立

由于航姿设备无纬度解算值,需要引入外部位置信息或速度信息[8～9],同时,在几乎所有舰艇上均有计程仪设备,可引入计程仪速度与航姿设备输出姿态、航向一起对跨纬度值进行计算,舰艇跨纬度值由舰艇航行情况确定。

外部计程仪提供准确的参考水平速度信息,航姿设备工作在捷联惯性导航阶段,实时解算出水平速度,解算出水平速度与外部参考速度之差作为观测量,则观测方程为

Z(t)=H(t)X(t)+ν(t)

(5)

连续的动态系统需离散化后才能在机上运行,式(3)与式(5)所描述的系统的离散化形式为

(6)

式中Φk,k-1为一步转移矩阵;Wk为系统激励白噪声序列;Vk为量测白噪声序列,δVk为不确定性输入(外界环境所造成的随机干扰输入)。同时Wk、Vk满足:

(7)

下面给出离散卡尔曼滤波方程:

1) 状态一步预测:

2) 状态估计:

3) 滤波增益:

4) 一步预测均方误差:

5) 估计均方误差:

系统由于存在不确定性量测输入(随机干扰),为了保证卡尔曼滤波的性能,滤波方程中用调谐后的R*阵代替R阵,由于R*的调谐有一个相当大的范围,因此可以通过仿真确定R*阵。

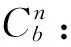
(8)

4 航行试验和仿真试验结果对比

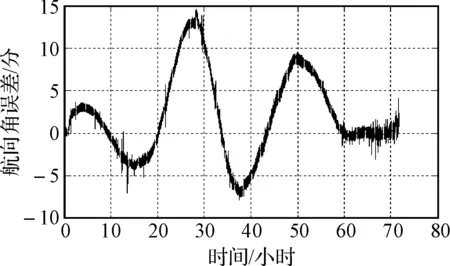
图1 组合计程仪信息的航行对准后继续航行72h的航向一次差曲线

图2 未组合计程仪信息的航行对准后继续航行72h的航向一次差仿真曲线

论文进行了航行状态下的组合对准方法实验,并继续航行了72h,航向一次差曲线如图1所示。随后使用该实船录取的数据,进行了未组合计程仪信息的事后仿真,时间同样为72h,一次差曲线如图2所示。

5 结语

综上所述,对比图1和图2可以看出,航行状态引入计程仪信息后,72小时内航向角误差得到了极大的缩小,极大的提高了设备精度,验证了该数学模型的可行性。

[1] 黄德鸣,程禄.惯性导航系统[M].北京:国防工业出版,1986.

[2] 万德钧,房建成.惯性导航初始对准[M].南京:东南大学出版社,1998.

[3] 郑梓祯,蔡迎波.舰艇导航系统试验与鉴定[M].北京:国防工业出版社,2005.

[4] 秦永元.惯性导航[M].北京:科学出版社,2006.

[5] KOHEI O.Initial Rapid Alignment/Calibration of a Marine Strapdown Inertial Navigation System under Motion[C]//Symposium Gyro Technology.Stuttgart,Germany,1993.

[6] 魏伟,秦永元,张晓东,等.卡尔曼滤波系统和量测噪声自适应估计的关联性[J].测控技术,2012,30(12):98-103.

[7] Jwo Dahjing,Wang Shenghang.Aptive fuzzy strong tracking extended Kalman filtering for GPS navigation[J].IEEE Sensors Jounrnal,2007,7(5):778-789.

[8] 李魁,王玮,刘芳,等.长航时惯导系统全阻尼综合校正算法[J].仪器仪表学报,2012,33(3):543-548.

[9] 赵龙,魏宇康,刘生炳,等.基于外测速度信息修正SINS姿态误差的H∞控制设计方法[J].导弹与航天运载技术,2014,334(4):28-31.

Integrated Algnment Algorithm of the Strapdown Attitude System in Sailing

LI Ying1YANG Xin2LI Bo3

(1.Unit 95,No.92941 Troops of PLA,Huludao 125001)(2.No.19 Central Xisanhuan Road,Beijng 100841)(3.Border Control Bureau of Tianjin Public Security,Tianjin 300457)

The strapdown attitude system has no latitude to be calculated,causing heading’s errors too large when the warship is cross-latitudes sailing.Log’s velocity with attitude and course of the strapdown attitude system is imported to calculate latitude,then mathematics model is established to process the initial alignment.Through sailing test,course error’s swing reduced much in 72h,the possibility of the mathematics’ model is verified that it can raise the accuracy of the system and has actual usage meaning.

strapdown attitude,attitude matrix,mathematics model,log’s velocity,Kalman filter

2014年8月3日,

2014年9月11日

李莹,女,工程师,研究方向:惯性导航系统试验与数据处理。

U666.1

10.3969/j.issn1672-9730.2015.02.016