舰载发射装置传递矩阵的建立*

梁洪涛 吴茂林 岳 强

(1.海军工程大学兵器工程系 武汉 430033)(2.91663部队计量站 青岛 266002)



舰载发射装置传递矩阵的建立*

梁洪涛1吴茂林1岳 强2

(1.海军工程大学兵器工程系 武汉 430033)(2.91663部队计量站 青岛 266002)

舰载火箭武器是我国近海作战的主要武器之一,作为鱼雷反潜盲区的补充,如何提高舰载火箭弹的射击效率对于提高部队战斗力具有重要的意义。舰载火箭发射系统是多刚柔体耦合系统。通过多体系统矩阵传递法,求出系统中每一个组成构件的传递方程,并通过传递矩阵的传递性质最终确定系统的传递总方程,为下一步求系统的动力响应提供理论基础。

舰载火箭; 刚柔耦合; 传递矩阵

Class Number TJ768.2

1 引言

舰载火箭武器是我国作为近海作战的主要武器之一,提高火箭武器的射击精度对于提高部队战斗力具有显著影响。本文以某型舰载火箭发射装置为研究对象,通过求解相邻构件之间的传递矩阵,最后得出系统的总传递方程,为研究火箭弹的起始扰动提供参考。

2 矩阵法概述

传递矩阵法以线性和非线性系统为研究对象,在线性系统中,主要解决了对象在静载荷下的变形、固有周期以及特征矢量的问题[1];在非线性系统中,结合多体系统传递矩阵法与有限元方法,对系统非周期激励下的响应,用离散时间传递矩阵法处理含有刚体和大变形梁大运动的非线性动力学问题。相对于传统的kane方法、schiehlen方法等。传递矩阵法具有如下的优点[2～5]: 1) 每种类型的元件都有自己的传递矩阵,一旦建立以后就可以直接套用,不需要重新求解; 2) 系统的总传递方程是每个单独元件传递矩阵的乘积,这种求总传递矩阵的方法大大提高了计算效率; 3) 不同时刻的位置和方位等变量对应的矢量都由这些先前时刻的值和边界条件得到。

3 系统模型及其状态矢量

3.1 系统建模

整个舰载发射系统由海平面、舰艇实体、发射装置等组成[6]。发射装置含有底座、机架、弧形摇架和发射管组等机构,根据功能和性质的不同,以及各部件在矩阵传递中的等效作用,把舰载火箭发射系统看成是体和铰的组合体。根据矩阵传递的需要,按照“体”和“铰”的原则,将舰载发射系统编号如下:

图1 舰载火箭发射系统模型

0(边界):海平面;1(弹性阻尼铰):海平面与舰艇的接触面;2(刚体):舰艇;3(弹性铰):舰艇与回转基座底座的接触面;4(刚体):底座;5(弹性铰):底座与回转基座的接触面;6(刚体):回转基座;7(弹性铰):回转基座与机架总成的接触面;8(刚体):机架总成;9(弹性铰):机架总成与高低传动机构的接触面;10(刚体):高低传动机构;11(弹性铰):高低传动机构与弧形摇架的接触面;12(刚体):弧形摇架;13～18(弹性铰):弧形摇架与六个发射管的接触面;19～24(刚体):发射管;25～30(边界):发射管与边界的接触面。所以此舰载火箭发射系统可以看成是由6个刚体、6个弹性体、1个分布基础弹性阻尼铰、11个弹性阻尼铰组成的非线性时变多刚柔体系统。

3.2 符号约定

系统中采用的坐标系均为笛卡尔坐标系。本文中系统的边界条件是发射管的前后端,从海平面至发射管前后端的方向为传递方向,根据系统的编号,传递方向是按照从小到大排列的。零部件的输入端为零部件对应的编号和其前一编号的组合,输出端为其和后一编号的组合,如对于零部件5,其输入端为p4,5,输出端为p5,6,相邻零部件的联接点既是前一零部件的输出端,也是后一零部件的的输入端。每个联接点pi,j的状态矢量用Zi,j表示。

在力学系统中,一个点的状态矢量是一个列阵,从一个点的状态矢量中,可以看出该点的几何位置以及力学状态,包括位移、角位移、力和力矩等。状态矢量是求解动力学方程的基础,尤其是在动力学仿真过程中,每一步的运动状态都必须由前一步的状态矢量确定后才能得出。在求解方程中,状态矢量相当于已知数,下一状态的状态矢量则对应于待求的未知量。

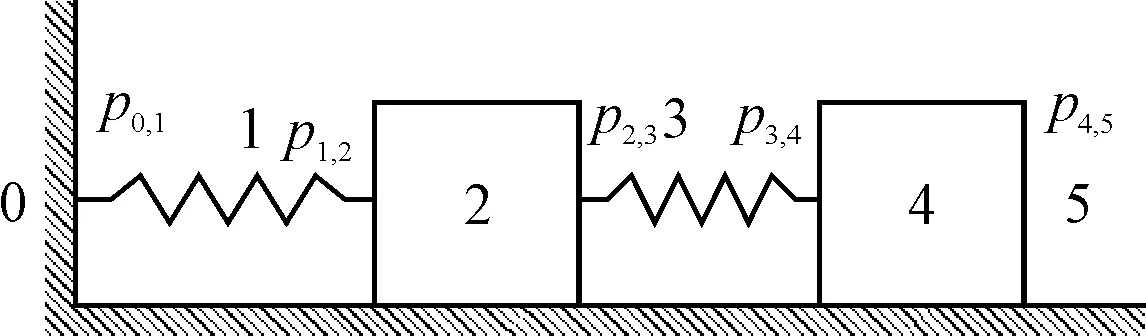
图2 质量与弹簧系统

如图2所示为由集中质量和弹簧组成的系统,元件的编号依次为0～5,则个元件联接点的状态矢量为

(1)

对于图2中的弹簧质量系统,设弹簧系数均为K,其边界的状态矢量Z0,1和Z4,5分别为

(2)

(3)

则其总传递方程为

(4)

3.3 系统状态矢量

模态坐标是为了描述方便,对于振动系统一般采用自然空间物理坐标,但由于系统各个未知数是耦合的,求解就非常麻烦,振动转化到模态坐标下即可利用正交特性独立求解未知数了。

由系统模型可知,整个发射系统共含有30个联接点,对系统的运动状态进行分析,定义各联接点的状态矢量为

(5)

(6)

(7)

Z8,9= [x,y,z,θx,θy,θz,mx,my,mz,

(8)

Z12,13～18= [x,y,z,θx,θy,θz,mx,my,mz,q1x,q1y,

(9)

Z13～18,19～24= [x,y,z,θx,θy,θz,mx,my,

(10)

Z19～24,25～30= [x,y,z,θx,θy,θz,mx,my,

(11)

Z3,4～Z7,8与Z1,2形式一致。

4 舰载发射系统的传递矩阵

在建立舰载火箭发射系统模型的基础上,通过分析系统中每一个联接点的状态矢量以及边界条件,利用多体矩阵传递法求出每一个相互联接点的传递矩阵后,通过矩阵乘法的运算即可得出系统的总传递方程。

4.1 海平面到舰艇表面的传递方程

舰艇在海浪中受到扰动后做六自由度的运动,分布是绕其横轴、纵轴和竖轴上的往复运动以及绕中心轴转动,绕横轴的往复运动称为横摆,绕纵轴和竖轴运动分别是纵摆和垂摆,绕三个中心轴转动的运动称为纵摇、横摇和首摇。舰艇在受到干扰力的作用下产生的上述运动称为强迫摇摆。舰艇受海水的作用可以由分布基础阻尼代替,当舰艇绕铅垂线转动时,波浪对舰艇只有阻尼作用;在舰艇做横摇和纵摇运动时,波浪对舰艇的作用可以等效为弹簧和阻尼的作用。根据文献可知,从海平面到舰艇边界的传递方程为

Z2,1=U1Z0,1

(12)

其中

(13)

-lx[u6,4u6,5(u6,6-1)]}

-lx[u6,7u6,8u6,9]}

-C*Dr0+C*Dr1

4.2 舰艇表面发射装置的传递矩阵

由第3节可知,舰艇是联接发射装置的载体,可将它看成是一个一端输入一端输出的空间运动刚体,其传递方程为

Z2,3=U2Z2,1

(14)

在上式中

(15)

其中

从舰艇到发射装置底座通过铰链联接,由于发射装置在舰艇上会振动,可把联接的铰链看成是空间弹性铰的联接,在分析弹性铰时可从纵向弹簧和扭簧方面入手,纵向弹簧表现为随着坐标系移动,扭簧等效于底座绕舰艇转动。则从舰艇到发射装置的传递方程可等效于空间弹性铰的传递方程:

Z4,3=U3Z2,3

(16)

上式中

(17)

其中

(18)

(19)

舰艇与回转基座通过底座联接,底座可以等效为一端输入一端输出的刚体,从底座的输入端到输出端的传递方程可参考空间运动刚体的传递方程:

Z4,5=U4Z4,3

(20)

U4与U2形式一致。

底座与回转基座之间通过铰链联接,其传递方程为

Z6,5=U5Z4,5

(21)

其中,

(22)

回转基座看成为一端输入一端输出的刚体,其传递方程为

Z6,7=U6Z6,5

(23)

U6与U4形式一致。

回转基座与机架采用铰链联接,其传递方程为

Z8,7=U7Z6,7

(24)

机架是一端输入两端输出的刚体,其传递方程为

Z8,9=U8Z8,7

(25)

机架至高低传动机构的传递为铰链联接的传递,其传递方程为

Z10,9=U9Z8,9

(26)

高低传动机构为一端输入一端输出的刚体,其传递方程为

Z11,10=U10Z10,9

(27)

从传动机构到弧形摇架采用铰链联接,其传递方程为

Z12,11=U11Z11,10

(28)

其中,U11为铰链联接的传递矩阵。

弧形摇架是从传动机构至发射管的联接刚体,其传递方程为:

Z12,11=U12Z12,13～18

(29)

其中,U12为一端输入六段输出的传递矩阵,如下:

(30)

联接弧形摇架与发射管的每个弹性铰均为内接刚体外接弹性体的铰链,其传递方程为

Z12,13～18=U13～18Z19～24,13～18

(31)

其中

(32)

六个发射管视为横向振动弹性体,从每个发射管到自由边界的传递方程分别为

Z19～24,25～30=U19～24Z19～24,13～18

(33)

其中,

(34)

式中各项相关参数见参考文献。

4.3 系统的总传递方程

在已知每个构件的传递方程的基础之上,系统的总传递方程为各个传递方程之间的乘积,由于矩阵的乘法不能交换前后顺序,否则得出的结果将会出错。

1) 从海平面到弧形摇架的传递方程为

UⅠ=U11U10…U1

(35)

2) 从弧形摇架与发射管的接触面(13～18)到自由边界(25～30)的传递方程为:

UⅡ=U13U19

(36)

UⅢ=U14U20

(37)

UⅣ=U15U21

(38)

UⅤ=U16U22

(39)

UⅥ=U17U23

(40)

UⅦ=U18U24

(41)

根据分叉系统的处理方法,可得系统的总传递方程为

UallZall=0

(42)

其中,

(43)

(44)

Uall为系统的总传递矩阵,边界条件为

(45)

Z19～24,25～30= [x,y,z,θx,θy,θz,mx,my,mz,

(46)

5 结语

通过建立舰载发射系统的传递方程,求得系统的传递矩阵,在一直边界条件下,可根据总方程求得每一连接点的状态矢量,从而得出系统的动力响应。

[1] 陈国光.多管火箭系统发射动力学研究[D].南京:南京理工大学,1995.

[2] Mddux, Gary A. Research, Evaluation and analysis of design changes to the MLRS Launcher and carrier,2000.

[3] 芮筱亭,贠来峰,陆毓琪,等.多体系统传递矩阵法及其应用[M].北京:科学出版社,2008:457-460.

[4] 华东水利学院.弹性力学问题的有限单元法[M].北京:水利电力出版社,1974.

[5] 姚立强.线性系统理论[M].成都:西南交通大学出版社,1988.

[6] 毛保全,张金忠,杨志良,等.车在武器发射动力学[M].北京:国防工业出版社,2010.

Establishment of Transfer Matrix in Shipboard Launching System

LIANG Hongtao1WU Maolin1YUE Qiang2

(1. Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033) (2. Metrology Station, No. 91663 Troops of PLA, Qingdao 266002)

Shipbased rocket weapon is one of the main weapons during the offshore operations. As the supplement of anti-submarine torpedoes in blind area, it is important to improve the shooting efficiency of shipbased rockets. Shipbased rocket launcher system consists of different flex and rigid bodies, dynamic response of the system determine initial disturbance during the shooting of rockets. Transfer equation by used of multi-body transfer matrix method is obtained, which provides a theoretical basis for the seeking of dynamic response.

shipbased rocket, rigid-flexible coupling, transfer matrix

2014年12月10日,

2015年1月27日

梁洪涛,男,硕士,研究方向:武器系统运用与保障工程。吴茂林,男,硕士生导师,研究方向:武器系统运用与保障工程。岳强,男,硕士,研究方向:兵器科学技术。

TJ768.2

10.3969/j.issn1672-9730.2015.06.038