基于PSO算法的共形集成天线综合性能优化*
2015-03-14隋景鹏赵晓楠李佳伟
隋景鹏 赵晓楠 李佳伟
(1.海军装备部舰船办公室 北京 100071)(2.中国舰船研究设计中心 武汉 430064)
基于PSO算法的共形集成天线综合性能优化*
隋景鹏1赵晓楠2李佳伟2
(1.海军装备部舰船办公室 北京 100071)(2.中国舰船研究设计中心 武汉 430064)
共形安装于特定平台、具有初步构型方案的复杂结构特型天线,其辐射全向性、定向增益、雷达波散射截面积等特性均需要满足特定的设计指标。同时,复杂天线的外形结构具有多个尺寸参数,均为详细设计的量化对象。为得到相对最优的天线详细设计方案,可针对天线的多个结构参数,将全波精确电磁计算方法和优化算法相结合,进行迭代。论文针对典型案例,通过粒子群(PSO)优化算法驱动矩量法(MoM),对特型天线的概念结构方案进行迭代优化,形成综合性能指标相对最优的设计方案。
共形集成天线; PSO算法; 多性能指标; 结构尺寸参数优化
Class Number TN82
1 引言
某特型V/UHF通信天线受其功能要求和安装平台可提供条件的限制,需采用多个宽度对称振子天线水平环绕金属柱状结构的形式。该天线需要承担的多种用途,决定了该天线在所有对称振子天线同时工作时,收/发具有全向性;部分对称振子天线工作时,具有较强的定向通信能力;同时,从整体平台隐身性指标出发,该天线还应具有尽可能低的雷达波散射截面积(RCS)。因此,在从简单天线形式构想形成实际具体天线的详细设计过程中,应当综合可虑上述三个方面的性能要求。基于计算电磁学的电磁仿真是一种低消耗、高效率的设计辅助手段,可有效评估设计方案的各种辐射、散射电磁特性。将电磁仿真与数值迭代优化相结合,可实现针对多指标的量化设计,确保优化方案权衡了不同方面的性能要求,达到综合最优。
本项目特型天线三个方面性能要求的主要表征量分别为:全向水平方向图均匀度、定向最大增益、隐身性。因此,可采用基于矩量法(MoM)的商业软件FEKO承担电磁仿真工作;另一方面,由于该天线的详细设计涉及对称振子天线的长度、宽度,对称振子天线至柱状结构的距离,柱状结构的横截面形状(圆形、多边形或花瓣形)与尺寸等多个参数,对于这种多目标、多参数的复杂问题,应选择高效的智能优化算法,本文应用的是粒子群(PSO)算法[1]。
2 研究对象的选取与优化目标的表征
为了完成电磁仿真与智能优化相迭代的设计过程,首先需要构建仿真模型,定义可改动的设计参数(即自变量),明确优化目标对应的表征参数(即因变量)。
2.1 仿真模型的构建
对于任何一种优化算法,必须进行足够次数的迭代运算,才能使优化结果与实际最优解的差异小于可承受误差。对于PSO优化算法,为了确保优化过程能够在整个搜索空间(由各个待优化参数的取值范围所构成)内进行,还需要设置足够多的粒子数。一般来说,粒子数不应少于20个,迭代次数应大于100,最少不得小于50。也就是说,对一个问题,需要进行最少1000次的求解才能获得优化结果[2]。如果问题的单次求解时间较长,整个优化过程则会花费漫长的时间。因此,应尽量控制仿真优化的模型大小。
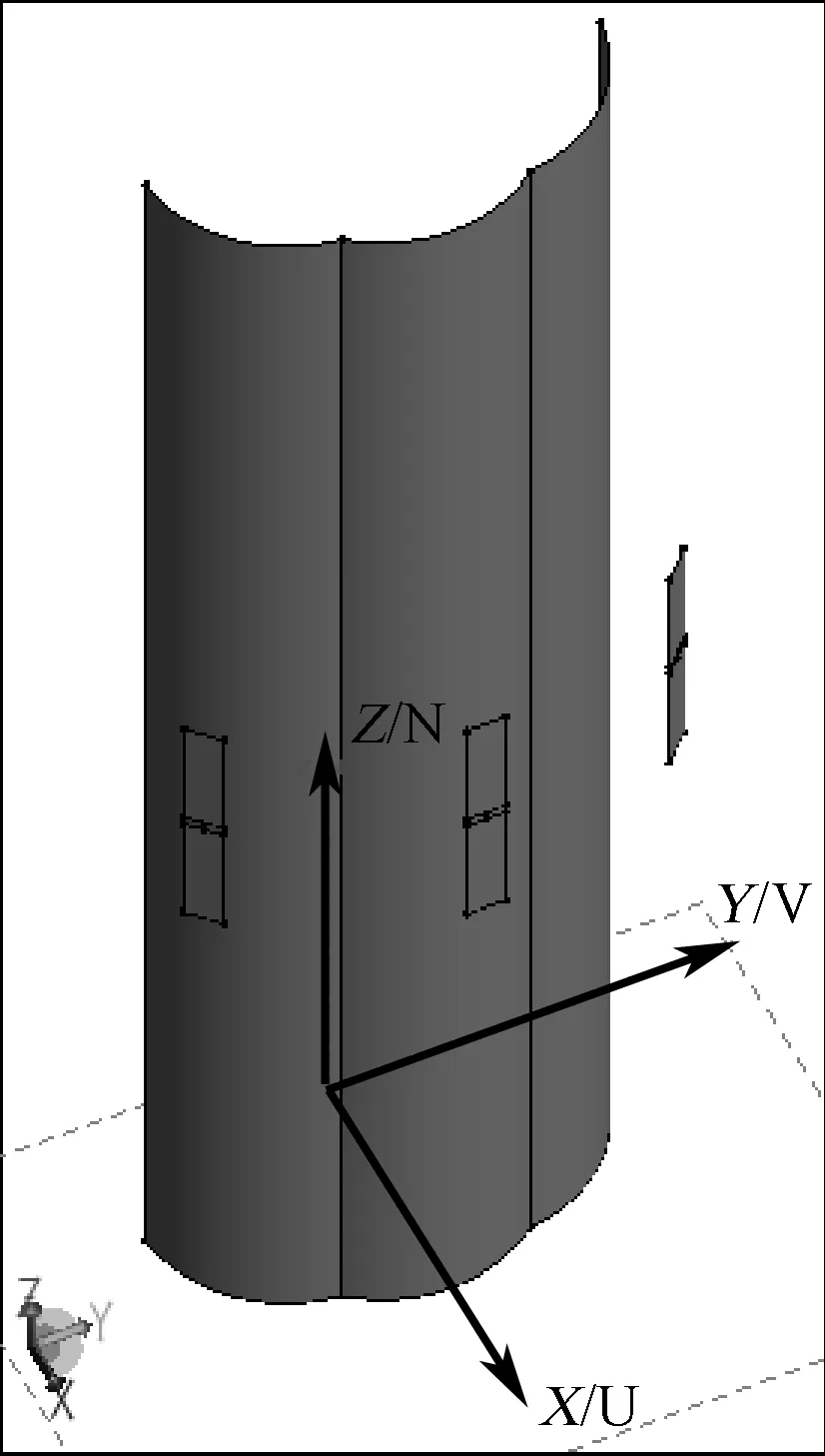
图1 共形集成天线仿真优化基础模型具体形状示意图
针对特型天线三个方面的性能要求,本研究优化的目标分别为提高全向水平方向图均匀度、增强定向最大增益和改善隐身性。定义单个对称振子天线与其对应的部分柱状结构(作为反射背板)共同组成一个天线单元,全向方向图是所有天线单元共同作用而形成的,其均匀度可由单个天线单元对应水平张角范围内,方向图增益的起伏来表征;定向增益则主要依托部分天线单元来实现,其最大值可由单个天线单元的方向图最大增益来表征。
因此,本文取三个天线单元作为仿真优化研究的基础模型(仅对中间的天线单元馈电),既能够有效控制单次仿真的计算量、降低迭代优化所需消耗的时间,又考虑相邻天线单元之间的结构电磁耦合效应,提高仿真预测的准确性。模型具体形状示意图如图1所示。
2.2 优化对象的表征
为实现参数化迭代,需对作为详细设计对象的各个天线结构尺寸参数进行定义,并以之为优化过程中的自变量。结合仿真优化模型的横截面图和侧视图,定义其各个结构尺寸的表征代号如下(如图2所示):
m为天线单元个数;a×b为对称振子天线长×宽;d为对称振子天线到背板中心距离;r1为背板弧度半径;r2为背板边缘到柱体中心;θ为背板弧度张角;为确保柱体结构封闭,θ应等于:
(1)
这些自变量参数的取值范围应根据宽带偶极子天线设计经验公式、平台设计的其他限制因素(如结构强度及重量要求、安装工艺要求)等进行设定。

图2 天线结构尺寸参数表示图
2.3 优化目标的表征
由于最大增益定义为“最大辐射方向的辐射强度与平均辐射强度之比”[3],水平方向上,在天线单元辐射功率相同的情况下,单个天线单元的最大增益越高,其在全向水平方向图中的贡献将造成整体方向图均匀度越差,即单个天线单元的高增益和天线整体水平方向图的高均匀度是两个相互制约的指标。同时,天线的RCS也与天线,特别是柱状结构的外形、尺寸紧密相关。
因此,针对本文确定的仿真模型,可将上述三个方面的性能要求用以下物理量进行表征,从而形成可量化的迭代优化目标。
定义一定水平方位角范围(-360°/m~360°/m)内中间天线单元方向图的增益最大值与最小值之差为ΔGm,来表征全向性均匀度;用中间天线单元的最大增益Max(G)来表征定向最大增益;隐身性则可表征为一定水平方位角范围(720°/m)内RCS的均值σmean。
3 目标函数的构建
为了使特型天线同时满足提高全向水平方向图均匀度、增强定向最大增益和改善隐身性三个方面的性能要求,需要设置目标函数对天线各个尺寸参数进行优化,寻找兼顾三个方面的自变量参数取值,以得到相对最优的天线详细设计方案。因此,目标函数应为天线各个尺寸参数所构成的函数表达式:
Fitness=g1[ΔGm(a,b,d,m,r1,r2)]
+g2[Max(G)(a,b,d,m,r1,r2)]
+g3[σmean(a,b,d,m,r1,r2)]
(2)
ΔGm越小,天线整体全向性均匀度越高;Max(G)越大,天线定向最大增益越强;σmean越小,天线隐身性越好。同时,为了适应天线的宽频段应用需求,并尽量简化目标函数以提高优化效率,本项目根据初步将目标函数设置为:
(3)
其中N为计算的频率点数量,λi为对应频率占的权重;g1,g2,g3依次为ΔGm、Max(G)和σmean的权重。这些权重系数的作用一方面是为了反映所对应目标参量的重要程度,对于本文研究的对象,辐射特性必须满足使用需求,应尽可能提高,而散射特性在RCS低于其分配指标值时,幅值的略微增长是设计方案可以承受的;另一方面,权重系数的取值还应确保目标函数各个组成部分的量级相当,以避免在优化过程中,出现某一目标参量取值过大,导致其他目标的影响被削弱甚至忽略的情况[7~8]。根据对初始模型的摸底仿真,结合设计需求对三个不同方面性能要求的侧重程度,对权重系数设定以下取值:
g1=30,g2=20,g3=1
(4)
优化的过程即是寻找使Fitness取最小值的参数。
4 PSO算法驱动FEKO软件仿真的迭代优化设计
4.1 算法简介
1) 计算电磁学矩量法(MoM)算法及FEKO软件
MoM算法是一种求解积分形式麦克斯韦方程的数值计算方法,其主要原理是将线性泛函方程离散化为线性矩阵方程,从而进行数值解算[4]。该算法基本概念清晰明了,处理方法灵活简易,适用范围广泛。
FEKO软件是一款以矩量法为基础的三维全波电磁场仿真软件,适合用于计算分析包含天线与装载平台的电大尺寸对象。
2) 粒子群(PSO)优化算法
4.2 PSO优化算法与FEKO软件的结合
FEKO软件自身具有基于多种不同算法的优化功能,但优化目标的可自定义性较差,复杂的目标函数无法设定;优化算法的收敛性和效率也难以验证;同时,对于同时包含辐射特性和散射特性的目标函数,在仿真中需要设置不同的模型进行计算,无法在同一模型中设置优化目标,也就是说FEKO软件不能实现本文提出的优化过程。因此需要编写相关程序,实现PSO优化算法的功能,并将FEKO软件与PSO优化算法相关联。
Python语言是一种面向对象、直译式计算机程序设计语言,其语法简捷而清晰,具有丰富和强大的类库,适用于快速生成程序的原型以及程序的最终界面。本文采用Python语言编写了程序模块和操作界面,实现PSO优化算法及其与FEKO软件的联动。
在此基础上,取式(3)的PSO适应度函数,对如前所述的自变量a,b,d,m,r1,r2进行优化。通过2000次的迭代,获得了以下优化结果:

表1 优化结果
可以看出,优化后天线的RCS稍有提高,但全向水平方向图均匀度和定向最大增益均得到明显的改善,优化效果符合预期目标。
5 结语
将智能优化算法与电磁仿真计算相结合应用于天线设计,是近年来随着计算机技术的发展而出现的一种复杂天线的设计方法。本文首次将此思路扩展到装载平台与天线共同设计的问题中,有效抽提出兼具模实性和低计算量的研究对象,综合考虑辐射特性和散射特性的多个相互关联、同时又互相制约的指标要求。这一方法具有较强的工程应用价值,适用于复杂大系统的一体化设计。
[1] J. Kennedy, R. Eberhart. Particle swarm optimization[C]//Proceedings of ICNN’95,1995,4:1942-1948.
[2] J. Robinson, Y. Rahmat-Samii. Particle Swarm Optimization in Electromagnetics[J]. IEEE Transactions on Antennas and Propagation,2004,52(2):397-407.
[3] D. W. Boeringer, D. H. Werner. Particle Swarm Optimization Versus Genetic Algorithms for Phased Array Synthesis[J]. IEEE Transactions on Antennas and Propagation,2004,52(3):771-779.
[4] E. C. Laskari, K. E. Parsopoulos, M. N. Vrahatis. Particle swarm optimization for integer programming[C]//Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02(Cat. No.02TH8600),2002,2:1582-1587.
[5] N. Jin, Y. Rahmat-Samii. Hybrid Real-Binary Particle Swarm Optimization(HPSO) in Engineering Electromagnetics[J]. IEEE Transactions on Antennas and Propagation,2010,58(12):3786-3794.
[6] S. Kitayama, M. Arakawa, K. Yamazaki. Penalty function approach for the mixed discrete nonlinear problems by particle swarm optimization[J]. Structural and Multidisciplinary Optimization,2006,32(3):191-202.
[7] M. F. Cardoso, R. L. Salcedo, S. F. de Azevedo, et al. A simulated annealing approach to the solution of minlp problems[J]. Computers & Chemical Engineering,1997,21(12):1349-1364.
[8] L. Yiqing, Y. Xigang, L. Yongjian. An improved PSO algorithm for solving non-convex NLP/MINLP problems with equality constraints[J]. Computers & Chemical Engineering,2007,31(3):153-162.
[9] 林昌禄,聂在平,肖笃墀,等.天线工程手册[M].北京:电子工业出版社,2002:10.
[10] 哈林登.计算电磁场的矩量法[M].北京:国防工业出版社,1981:6.
Multiple-Performance Optimization for Conformal Integral Antenna Based on PSO
SUI Jingpeng1ZHAO Xiaonan2LI Jiawei2
(1. Shipping Office, Naval Equipment Department, Beijing 100071) (2. China Ship Development and Design Center, Wuhan 430064)
For the antennas which conformal to the specific platform for specific use, the design starting from an initial configuration scheme should focus on different kinds of antenna performances, including ideal omni-directional pattern, high directive gain, and its RCS. In order to achieve the relative optimal design scheme, simulation with full-wave algorithm should be combined with numerical optimization for variable structure dimensions of the antenna. In this paper, with MoM diven by PSO, the conceptual design of an antenna with special form is optimized. After thousands of iterations, the design with an optimum overall performance is obtained.
conformal integral antenna, PSO, multiple performance, numerical optimization for variable structure dimensions
2014年12月17日,
2015年2月1日
隋景鹏,男,工程师,研究方向:舰船总体技术。赵晓楠,女,硕士研究生,工程师,研究方向:舰船电磁兼容。
TN82
10.3969/j.issn1672-9730.2015.06.037
