高频驻波天线的MoM-UTD分析*

刘 斌 黄付庆 陈伟尚 于秋杰

(1.中国电波传播研究所 青岛 266107)(2.总参信息化部驻济南地区军代室 济南 250013)



高频驻波天线的MoM-UTD分析*

刘 斌1黄付庆2陈伟尚1于秋杰1

(1.中国电波传播研究所 青岛 266107)(2.总参信息化部驻济南地区军代室 济南 250013)

论文首先依据矩量法对偶极子天线和对数周期天线上的电流分布进行计算,再根据电流分布得出远场和近场的场强波瓣图,并在此基础上利用一致性几何绕射理论分别计算了天线附近存在电大、电小尺寸导体时天线场强波瓣图的变化。

近场; 矩量法; 一致性几何绕射理论

Class Number TN822

1 引言

随着科学技术的发展,电子战在现代战争中的所起到的作用越来越突出。在高技术战争条件下的今天,各类武器平台装载了通信、导航、气象、雷达、电子战、无线电制导等电子设备,这些设备频段集中,密集分布在有限的区域内,而且要同时工作,相互之间的干扰也极易发生,这种情况的分析不能简单用天线远场方向图进行叠加,因为各类天线距离很近,不符合远场近场的划分条件,而在天线近场区域,则需要考虑的是天线感应情况。本文采用矩量法,对以对称偶极子天线和对数周期天线为代表的驻波天线近场进行了分析,并在此基础上利用一致性几何绕射理论分别计算了天线附近存在电大、电小尺寸导体时天线近场的变化,对天线近场的分析方法有一定指导意义。

2 矩量法介绍[2,4]

矩量法的基本思想[2]是将一个泛函方程化为矩阵方程,然后用人们熟知的方法求解该矩阵方程。例如要求解非齐次方程:

L(f)=g

(1)

式中L是线性算子,g为已知函数,f为未知函数。令f在L的定义域中展开为

(2)

式中an是系数,fn称为展开函数或基函数。在L的值域内定义一个权函数或检验函数ω1,ω2,ω3…的集合,对式(1)左右取内积并将式(2)代入,利用算子L的线性和内积的特性可以得到:

(3)

此方程组可以写成如下的矩阵形式:

[lmn][an]=[gm]

(4)

可见,通过矩阵求逆的办法可以对未知函数f进行求解。下面针对我们关心的线天线电流分布问题建立积分方程,并进行求解。

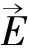
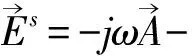
(5)

(6)

(7)

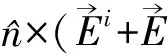
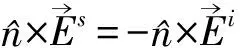
(8)

对于任意的一根细导线,可作如下近似:

1) 假定电流只是沿着导线轴的方向流动;

在以上假设的基础上可以得到电流的线积分方程,在线天线表面使用边界条件(8),并根据矩量法进行求解。

3 驻波天线的矩量法分析

3.1 偶极子天线场强波瓣图

以偶极子天线为例分析驻波天线的近场问题。在计算天线近场的时候,传统的远场辐射方向图不再适用,正确的解决方法是将天线按照一定的规则划分为多个小段,利用矩量法求出各个小段上的电流分布,然后根据电流分布来确定近场区域的场强分布情况。严格求解天线上的电流分布是一个非常复杂的理论问题,工程上对于结构简单的细长天线是利用无损好均匀传输现的理论来近似确定其电流分布。

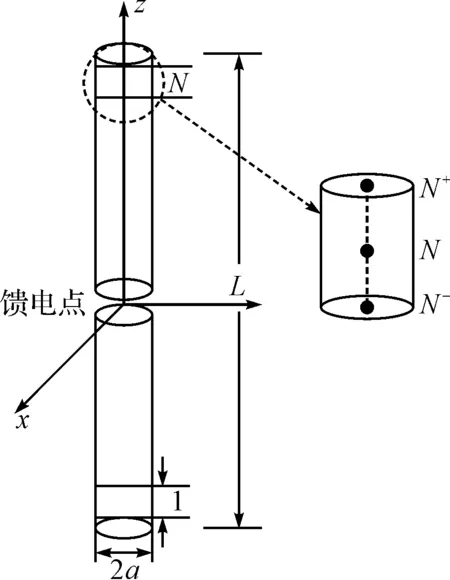
图1 偶极子天线

对中间馈电的偶极子而言,其可以看成是由张开末端开路的均匀传输线获得的,天线上的电流分布是对称于中点的驻波。如图1所示将偶极子天线分成多个小段,各个小段中需要考虑的是小段的中点和上下两个顶点。

对式(5)、式(6)进行各个小段的分析处理:

此时选用脉冲函数作为基函数去逼近天线上的电流分布[7]:

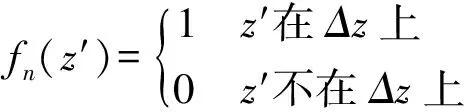
以狄拉克函数W=δ(z-zm)作为检验函数,其中选择的点分别为各个小段的中点即m=m1,2,…,N。

首先根据Zmn=Ei(m)·Δlm/I(n)计算出各小段的自阻抗和与其它小段的互阻抗,形成下列矩阵:

然后由[V]=[Z][I]可得[I]=[Z-1][V][8],从而得到各段的电流分布。

以频率为30MHz,长度为1/2波长,半径为0.01倍波长的中间馈电偶极子为例,将其分为11段进行计算,得出的电流实部和虚部分布如图2所示。

图2与文献[5]中的图2～图3从数值和变化趋势上都比较吻合,将偶极子垂直放置,馈电点取为坐标原点,根据电流分布分别计算出远场波瓣图和近场3m、4m、5m、8m处波瓣图如图3所示。

由图3(a)可见,对于工作波长为10m的半波偶极子天线,在距离天线100m和10000m处的归一化场强波瓣图几乎完全重合,这就说明了远场方向图与距离无关。再看图3(b),随着场点到天线距离的拉近,场强波瓣图发生剧烈的变化,距离为8m时,在天线轴向可以看到明显的凸起,随着距离越来越近凸起越发明显,而最大增益方向也由径向变为轴向,最后形成对天线阵子的一个包络。同时从图4还可以看出,在近场区域,场强波瓣图对于z=0平面不再对称,这是由两个阵子电流的同向流动引起的。

图2 半波偶极子天线电流实部/虚部分布图

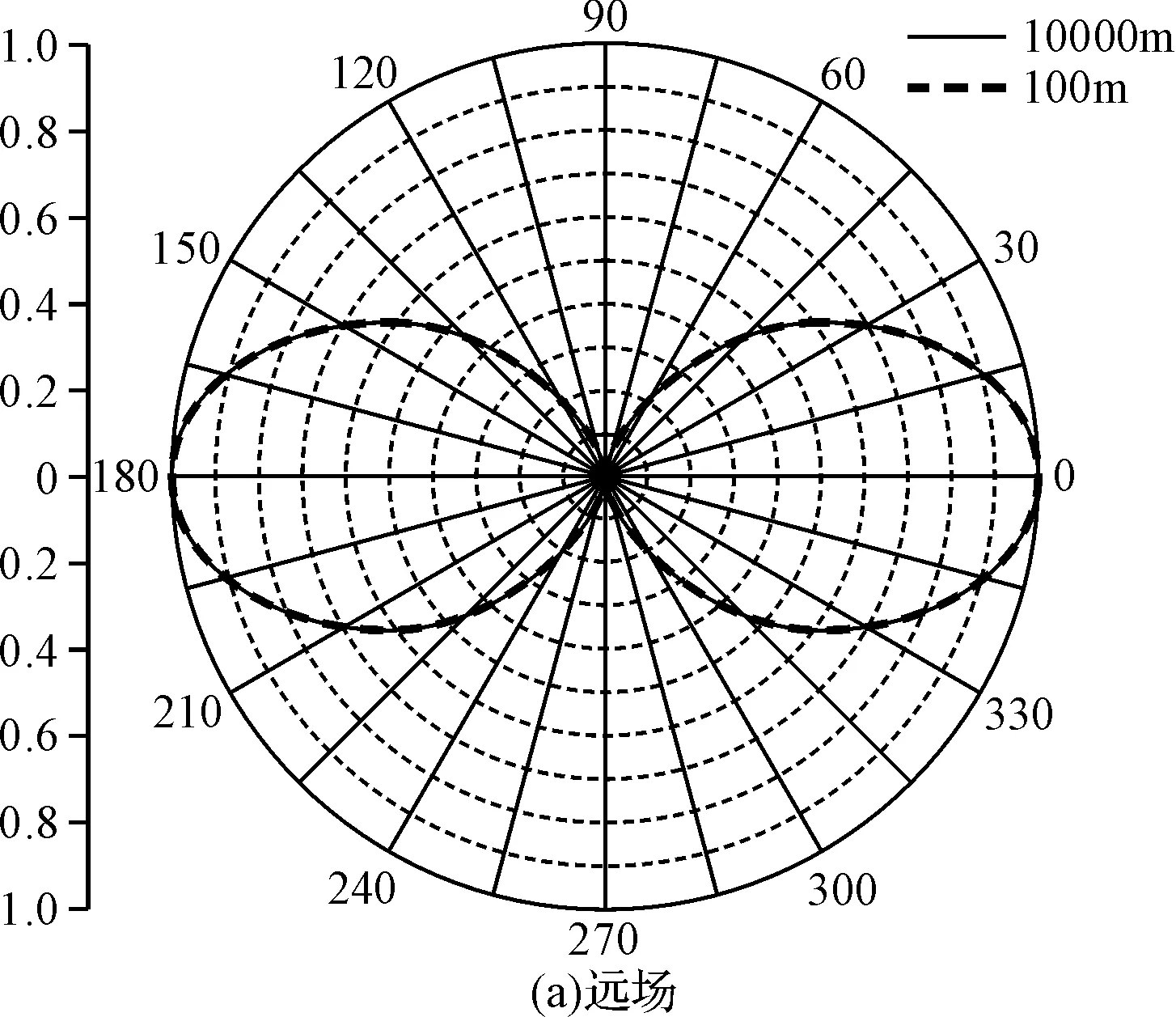
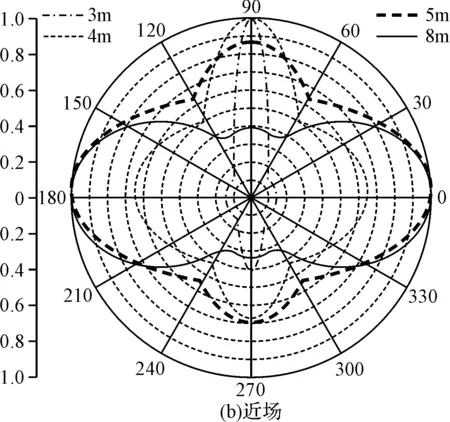
图3 偶极子天线归一化场强波瓣图

文献[1]中天线远场与近场的划分边界取半径R=2L2/λ,在这里R=5m。而从图3(b)可以看出距离8m时天线波瓣图在轴向上与远场波瓣图有明显的区别,这时若继续采用远场方法进行计算就会引起较大误差。通过计算得到10m处的波瓣图已经出现轴向凸起,因而建议在距离接近或小于一个波长的时候都采用近场方法计算,这样才能得到较为准确的结果。

3.2 对数周期天线场强波瓣图

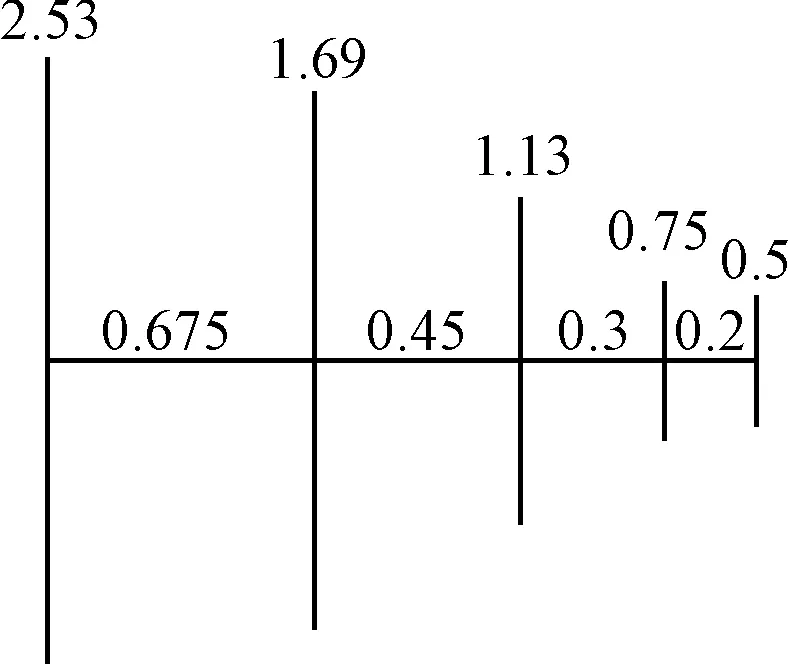
图4 对数周期天线示意图(单位m)

对数周期天线可以看作是由按照一定规律排列的不同长度的偶极子天线组成。由于各偶极子的工作频段相互补充,构成了对数周期天线较宽的工作频段。在30MHz频率下计算如图4所示的对数周期天线[9]。

按照第3节所述的计算方式得到互阻抗和各个振子分段的电流分布,进而得出远近场方向图如图5所示。

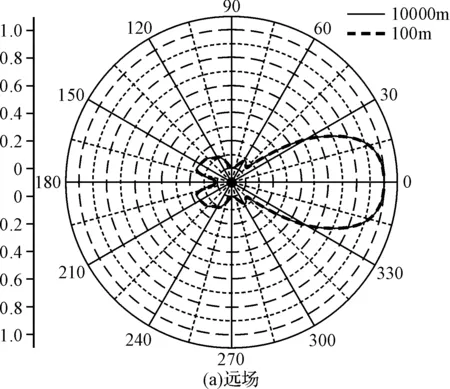
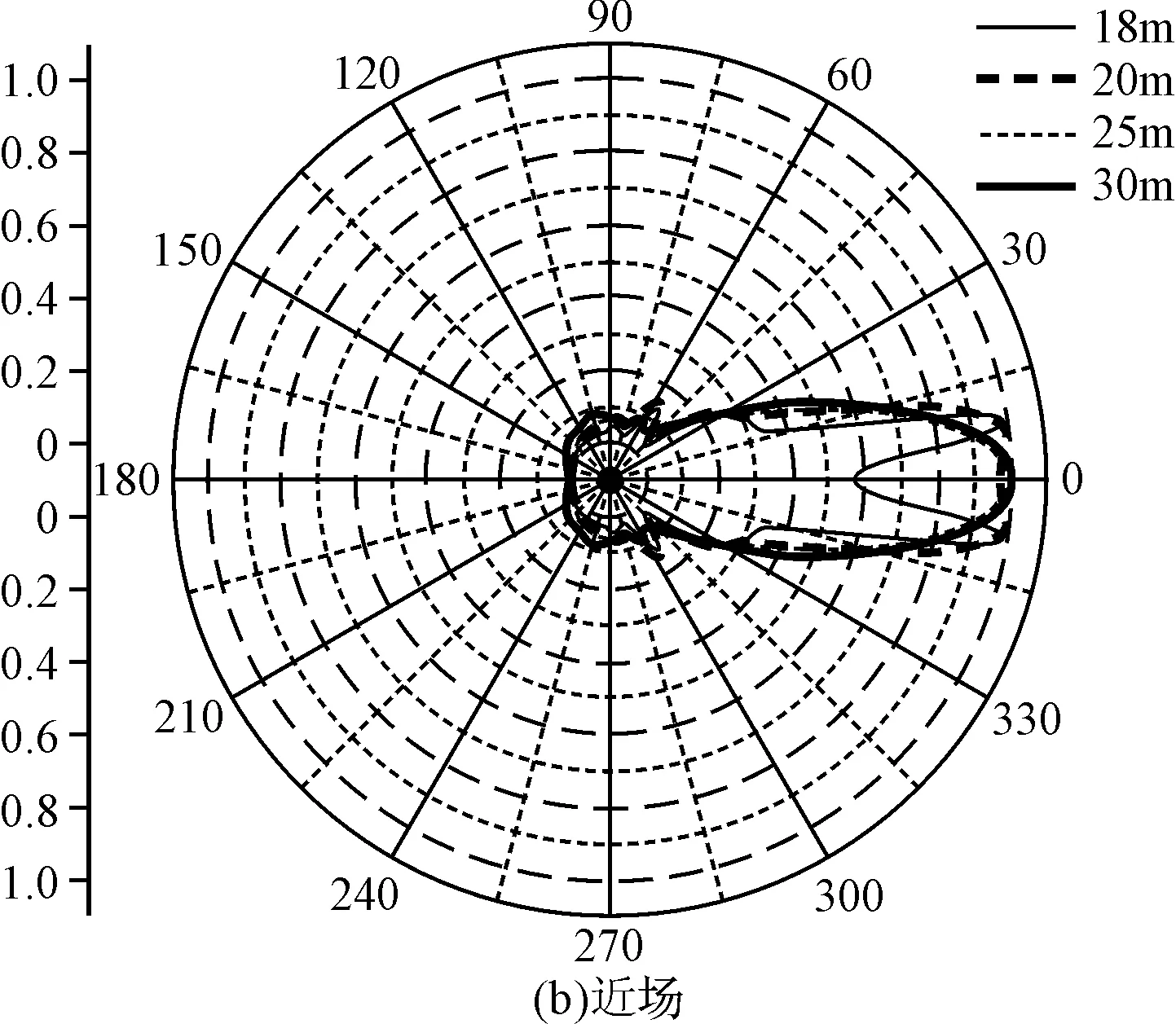
图5 对数周期天线近场归一化场强波瓣图

分析可知,30MHz为最短偶极子的共振频率,后面较长的偶极子与最短偶极子产生耦合,起到反射器的作用,从而使对数周期天线具有较强的方向性。由图5(b)可见,在距离天线馈电中心30m和25m时天线还是单主瓣的,随着距离接近到20m时,主瓣开始凹陷,到18m已经明显出现分叉,主瓣不再沿着对数周期天线的轴向了。分析后得知:因为随着距离的拉近,每个偶极子天线的最大辐射方向发生了变化,由径向变成轴向,有变成振子包络的趋势,那么由各个偶极子天线复合而成的对数周期天线的最大辐射方向也就不会再维持远场时的方向了。

4 几何绕射理论与矩量法结合

对于复杂电磁环境,由于多种导电散射体同时存在的复杂性,很多求解电磁问题的常用方法都很难应用。矩量法被认为是解决电小尺寸物体的辐射和散射等问题的一种有力工具,当电尺寸增大时,矩量法就受到计算机容量和计算时间、精度的限制。而几何绕射理论可用于这种大电尺寸的物体。但是必须事先知道线天线的电流,而当散射体离天线很近时,它对天线的电流就会产生影响。因此合适地结合矩量法和几何绕射理论,即采用两者的混合技术是非常有用的。

4.1 几何绕射理论分析电尺寸大导体

首先对导电平台某个边缘的绕射线进行分析,作如下例子。

图6 放置在导电平台的偶极子天线

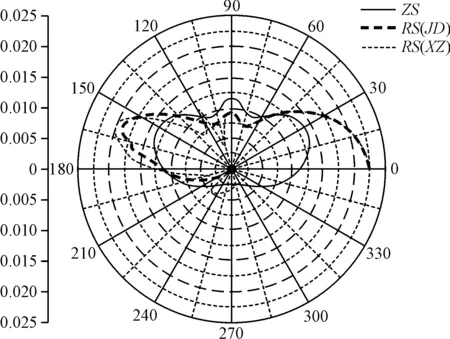
图7 综合场强波瓣图

图6中h为偶极子天线高度,d为平台绕射点距离O点的距离,分散的箭头表示绕射线。依据两种方法分别对其进行分析,一种采用无修正的半平面绕射方法,一种采用一致性几何绕射理论进行分析,结果如图7所示。

图7中ZS线表示无导电平台时,以O点为参考点的场强波瓣图,RS(JD)曲线表示存在导电平台时采用无修正的半平面绕射方法计算的场强波瓣图,RS(XZ)曲线表示采用一致性几何绕射理论计算的场强波瓣图。后两者都是存在直射、反射和绕射的情况。

4.2 矩量法分析电小尺寸导体

长条形导体主要指横向尺寸比较小的导体,对这些导体作如下近似:长条形导体的存在对线天线电流的影响忽略不计,用多根线状导体代替长条形导体。在这两种近似条件下采用矩量法的全域基点选配来求出线状散射体上的电流。激励起电流的源正是线天线的近场和其它散射体的散射近场。根据得到的激励场E′有:

L(I)=E′

如对偶极子周围有一长条形导电体,如图8所示,得出的强波瓣图见图9。

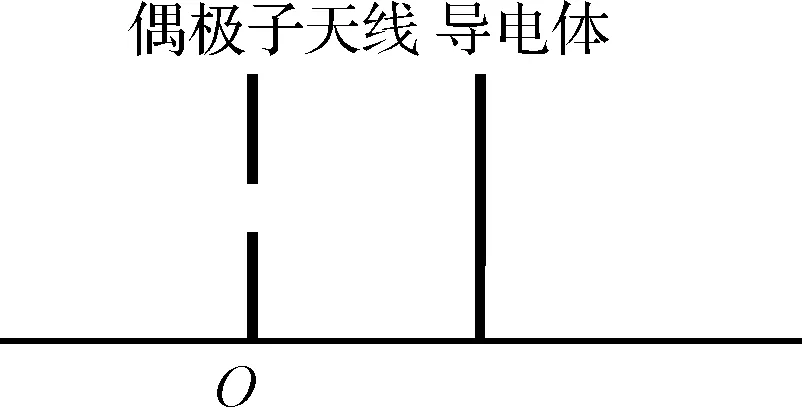
图8 偶极子天线旁长条形导体图

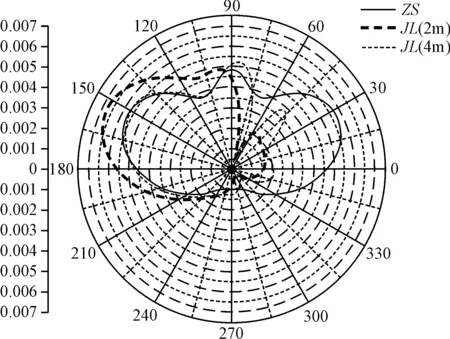
图9 偶极子天线受长条形导体影响场强图

图中ZS曲线以O点为参考点的场强波瓣图,JL(2m)表示导电体距离偶极子天线两米时的场强波瓣图,JL(4m)表示导电体距离偶极子天线4m时的场强波瓣图。从图中可以看出,导体的存在起到了反射器的作用,使得波瓣方向图变化较大,这也从另一个方面解释了对数周期天线方向性的形成。

5 结语

舰船上的电磁兼容分析是天线近场应用比较广泛的地方,由于空间的限制及大量用频设备的存在,需要对天线近场本身的分析及周围导电体的绕射,反射等情况进行分析。一般的原则都是将实际的复杂结构简化为用圆柱、圆球、立方体、线状结构等进行分析。在天线近场区内,电场有显著的径向分量,其功率流并不完全是径向的,场波瓣图通常依赖于距离。因此在近场区域需要通过严格的计算电流分布情况来获得场点的场强值,从而得到更为准确的电磁兼容分析结果。

[1] John D. Kraus, Ronald J. Marhefka.天线[M].章文勋,译.北京:电子工业出版社,2006:30-31.

[2] R. F. Harrington.计算电磁场的矩量法[M].王尔杰,肖良勇,等译.北京:国防工业出版社,1981:73-83.

[3] 谢处方.电波与天线[M].北京:人民邮电出版社,1966:1-12.

[4] 谢处方.近代天线理论[M].成都:成都电讯工程学院出版社,1987:27-30.

[5] 李世智.电磁辐射与散射问题的矩量法[M].北京:电子工业出版社,1987:67-88.

[6] 林昌禄.天线工程手册[M].北京:电子工业出版社,2002:31-33.

[7] 肖志文,等.偶极子天线矩量法分析[J].信息技术,2005,1:35-36.

[8] 周波,等.短波双极天线矩量法分析[J].信息工程大学学报,2008,(3):59-62.

[9] RECOMMENDATION ITU-R BS.705-1,1990-1995.

[10] 汪茂光.几何绕射理论[M].西安:西安电子科技大学出版社,1994:114-120.

[11] 陈伟尚,刘斌.基于矩量法的天线近场分析[J].舰船电子工程,2008,(11):181-183.

Analysis of HF Standing-wave Antennas Based on MoM-UTD

LIU Bin1HUANG Fuqing2CHEN Weishang1YU Qiujie1

(1. China Research Institute of Radiowave Propagation, Qingdao 266107) (2. Military Representative Office of Information Unit of the Headquarters of General Staff in Jinan, Jinan 250013)

Dipole antenna and log-periodic antennas are analyzed using the method of moment. The antenna is divided into segments and the currents are calculated on each segment, and the lobe pattern of far-field and near-field are obtained through the distribution of current. Furthermore, the near-field changes when there are electrically large and electrically small conductors exist near the antenna based on the uniform theory of diffraction are calculated.

near-field, method of moment, the uniform theory of diffraction

2015年2月11日,

2015年3月23日

刘斌,女,硕士,工程师,研究方向:天线分析。黄付庆,男,硕士,工程师,研究方向:微波通信装备和卫星通信装备的质量监督与研究。陈伟尚,男,高级工程师,研究方向:电磁兼容性分析。于秋杰,男,工程师,研究方向:计算机软件工程与频谱应用。

TN822

10.3969/j.issn1672-9730.2015.08.019