低频球面声波在水-空界面传播特性的研究*
2015-03-14陶智冯博
陶 智 冯 博
(1.海装装备采购中心 北京 100071)(2.沈阳辽海装备有限责任公司 沈阳 110003)
低频球面声波在水-空界面传播特性的研究*
陶 智1冯 博2
(1.海装装备采购中心 北京 100071)(2.沈阳辽海装备有限责任公司 沈阳 110003)
由于水和空气特性阻抗存在很大差异,传统的射线理论认为水-空界面的声透射性十分微弱。论文在射线方法的基础上,使用波动方法对球面声波跨水-空界面传播问题进行了深入研究。当声源位于水下较小深度时,随着频率的降低,被射线理论忽视了的非均匀波的作用显著加强,使得透射出水-空界面的声能量有了很大程度的增加。水下声能量随频率变化是由于直达波和界面反射波的干涉作用。射线结果是高频情况下波动结果的近似。
水-空界面; 均匀波; 非均匀波; 干涉
Class Number TN2
1 引言
由于空气中大量存在的噪声源可能对海底生物产生影响,以及军事上潜艇探测反潜飞机的需要,长期以来人们对声波在空-水界面的传播问题十分关注,却未能重视水-空界面对声波传播的影响,即声波由水传入空气中的情形。依据射线声学理论,由于水和空气特性阻抗的差异较大,水下声源产生的能量只有很少部分透射入空气。然而近年来,O.A. Godin和B.E. McDonald等发现低频声波在透过水-空界面时大部分能量能够透射到空气中[1~6],改变了人们以往的认识。这种显著提高的声透射性将有很大的应用前景,如在空气中直接探测海底地震产生的低频噪声,提前预报此类自然灾害,减少损失,为空中探潜提供了可能性等。
基于此,本文分别从射线理论和波动理论的角度出发,对球面声波在水-空界面的传播问题进行了详细讨论,其中假设界面两侧均是均匀半无限大空间。文章主要分析计算了透射入空气中及辐射到水中的声能量,并对两种方法的结论进行了比较。波动结果表明,深度很浅的单极子点声源产生的能量,透射进入空气的部分随频率的降低而显著增强,同时解释了非均匀波是造成此现象的主要原因。两种方法对水中声能量的计算结果近似一致,它随频率变化的原因来自于直达波和界面反射波的干涉作用。文章最后给出了数值仿真结果。
2 球面声波在水-空界面传播的射线模型研究
2.1 空气中透射能量的计算
水中的单极子点声源(monopole source)向外辐射球面波,声压可简单写成如下形式[7]:
p0=eikr/r
(1)
这里忽略了时间因子e-iωt。
射线方法将声源发出的球面波看成一条条声线,入射到水-空界面后,发生如同平面波一样的反射和折射,如图1所示。
将声线OAP和OA′P′分别绕z轴旋转一周,形成两个曲面,两者之间的所有声线构成一个声线管。设Io为水中声源单位距离处的声强,So为此处声线管横截面积;接收器P处的声强为Ip,声线管横截面积为Sp;各参数满足关系式IpSp=TEIoSo,其中TE是平面波能量透射系数[8]。依据声线管内的能量守恒,通过积分求得球面波通过水-空界面后的透射能量:
(2)
式(2)中Eo是无界面时声源的总能量输出,m=0.0012是空气和水的密度比,n=4.3是水相对于空气的折射率。求得Ea/Eo=2.8284×10-4,约为-35.5dB。由此可见,球面声波透射到空气中的能量很少,且与频率无关。射线结果表明水-空界面不是良好的声能透射面。
2.2 水中声场能量的计算
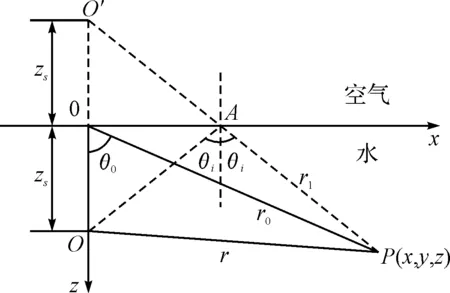
图2 水下声反射示意图
图2中,反射波被看成是由虚源O′发出。接收点P的声压由经OP的直达波和经O′AP的反射波叠加而成,求得其表达式如下[7]:
p=eikwr/r+eikwr1/r1
=-(2i/r0)sin(kwzscosθ0)exp(ikwr0)
(3))
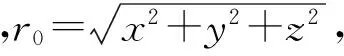
(4)
其中Eo=2π(ρwcw)-1[7]。用Eo将Ew归一化得:
Ew/Eo=1-(2kwzs)-1sin2kwzs
(5)
式中kwzs=2πzs/λw,λw是水中波长。
由于直达波与反射波到达水下固定点时相位差恒定,会发生干涉作用[9],使得水中的声能量Ew分布起伏不定,如图3所示,其中Ew已被Eo归一化。当zs/λw→∞,由于直达波与反射波的相互干涉作用逐渐减弱,Ew→Eo;而当zs/λw→0,即声波波长很长或声源很靠近分界面时,直达波与反射波的相互干涉是相消性的,Ew→0;在zs/λw=3/8时,直达波与反射波发生相长性干涉,Ew达到最大,此时Ew≈1.2Eo。
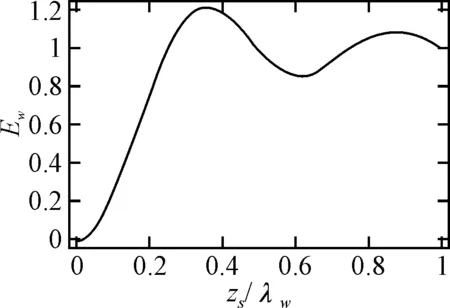
图3 水中总能量输出随声源深度变化曲线
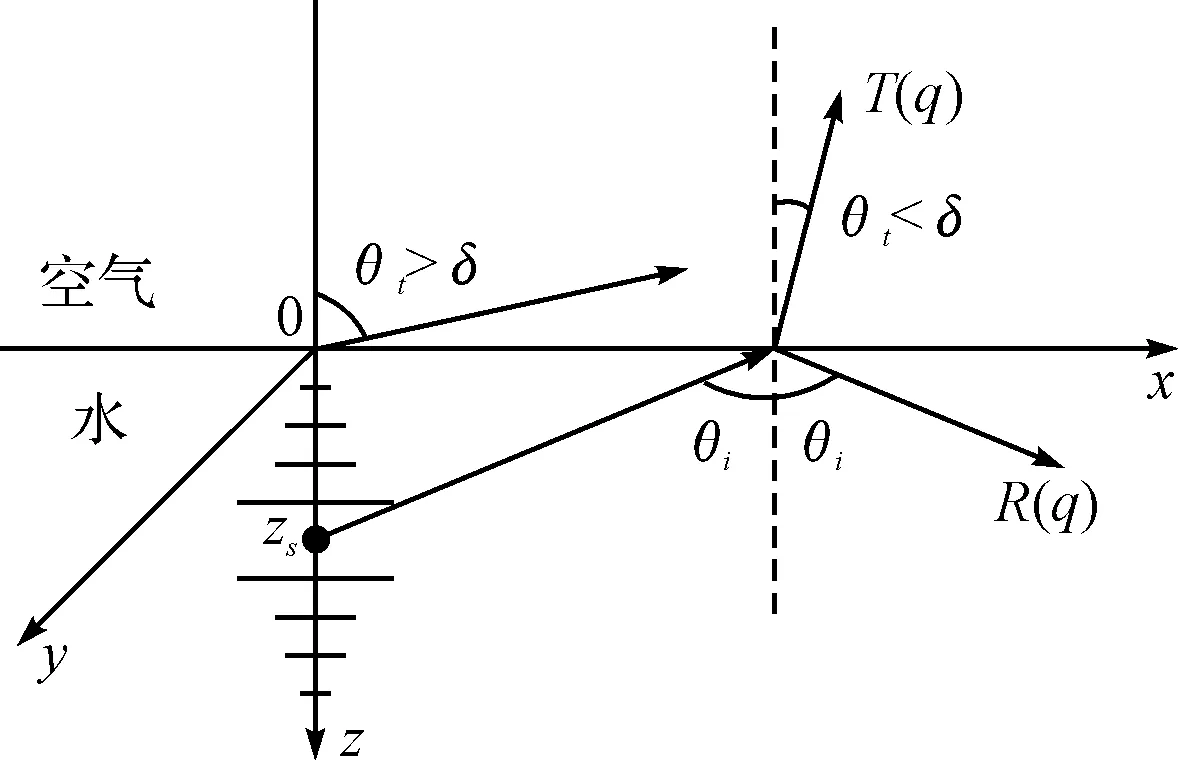
图4 平面波在水空界面的反射和折射情况
3 球面声波在水-空界面传播的波动模型研究
3.1 球面波的平面波分解
图4中θi为入射角,θt为折射角,临界角δ=arcsinn-1≈13.45°。假设单极子点声源位于水下坐标(0,0,zs)处,zs>0。将式(1)所示的球面波作平面波分解后,入射波、反射波和折射波可用以下各积分式表达[10]:
(6)
(7)
(8)
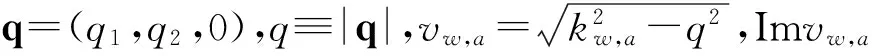
R=(mvw-va)/(mvw+va)
T=2mvw/(mvw+va)
(9)
由Snell定律知,在反射和折射时波矢的垂直成分改变,而水平成分保持不变。所以平面反射波和折射波的波矢分别为(q1,q2,vw)、(q1,q2,-va)。满足0≤q≤kw(Imvw=0)条件的平面声波在水下是均匀波(homogeneous wave),空气中的折射波也是均匀波,折射角0≤θt≤δ;满足kw
3.2 能量计算
平均声强由下式给出[10]:

(10)
其中(*)表示复共轭。透射到空气中的总能量可用声强垂直于水-空界面的分量在界面上的积分得到。结合式(6)~式(10)有:
(11)
同理求得水中的总声能量为
(12)
依据积分区间的不同,将Ea写成以下形式:
Ea=Eo[A1(m,n)+A2(m,n,kw,zs)]
(13)
式(3)中A1描述了均匀波的能量贡献,A2描述了在水中是非均匀波而折射到空气中是均匀波的能量贡献。在水中和空气中都是非均匀的波,由于声强没有虚部,所以对透射能量没有影响。令s=sin2θi,b=kwzw=2πzs/λw,求得A1、A2如下:
(14)
(15)
比较式(2)和式(14),易见两者相同,当频率增大时,b→∞,则A2→0,结合式(13)知,波动结果此时近似等于射线结果;但频率降低时,b→0,A2的作用将越来越明显,透射到空气中的声能量,式(13)的波动结果会比式(2)的射线结果高出十几分贝,如图5中的曲线1、2,其分别对应两种方法计算的Ea曲线。由此可见,水-空界面对低频声能的透射性比高频好。式(5)和式(12)的数值计算结果表明,射入水中的能量Ew,两种方法的结果相差不大,这是因为非均匀波对水下声能量没有影响,Ew随频率的变化来自于直达波和反射波的干涉作用。图中曲线3即是两种方法计算出的Ew的重合曲线。其中Ea、Ew均被Eo归一化。
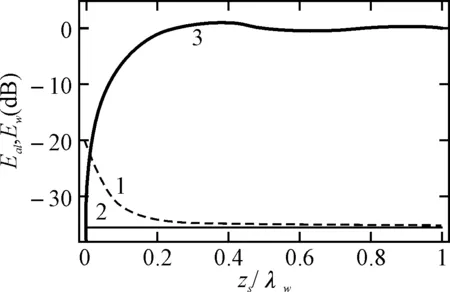
图5 水中和透射到空气中的声能量

图6 非均匀波与均匀波的比较
非均匀波相对于均匀波的贡献率E=10log10A2/A1清晰地描述了非均匀波的显著作用,如图6所示。显而易见,当zs/λw很小时,非均匀波对透射到空气中的能量的贡献远远大于均匀波,从而使得水-空界面成为良好的低频声能透射面。
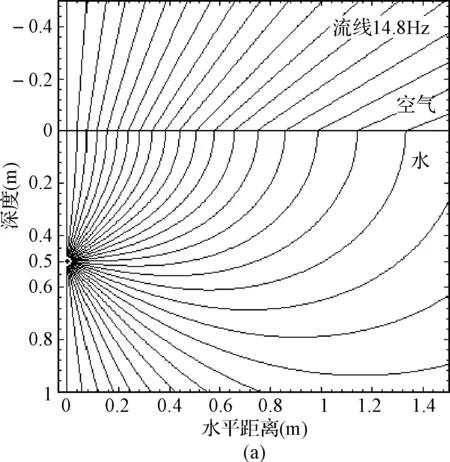
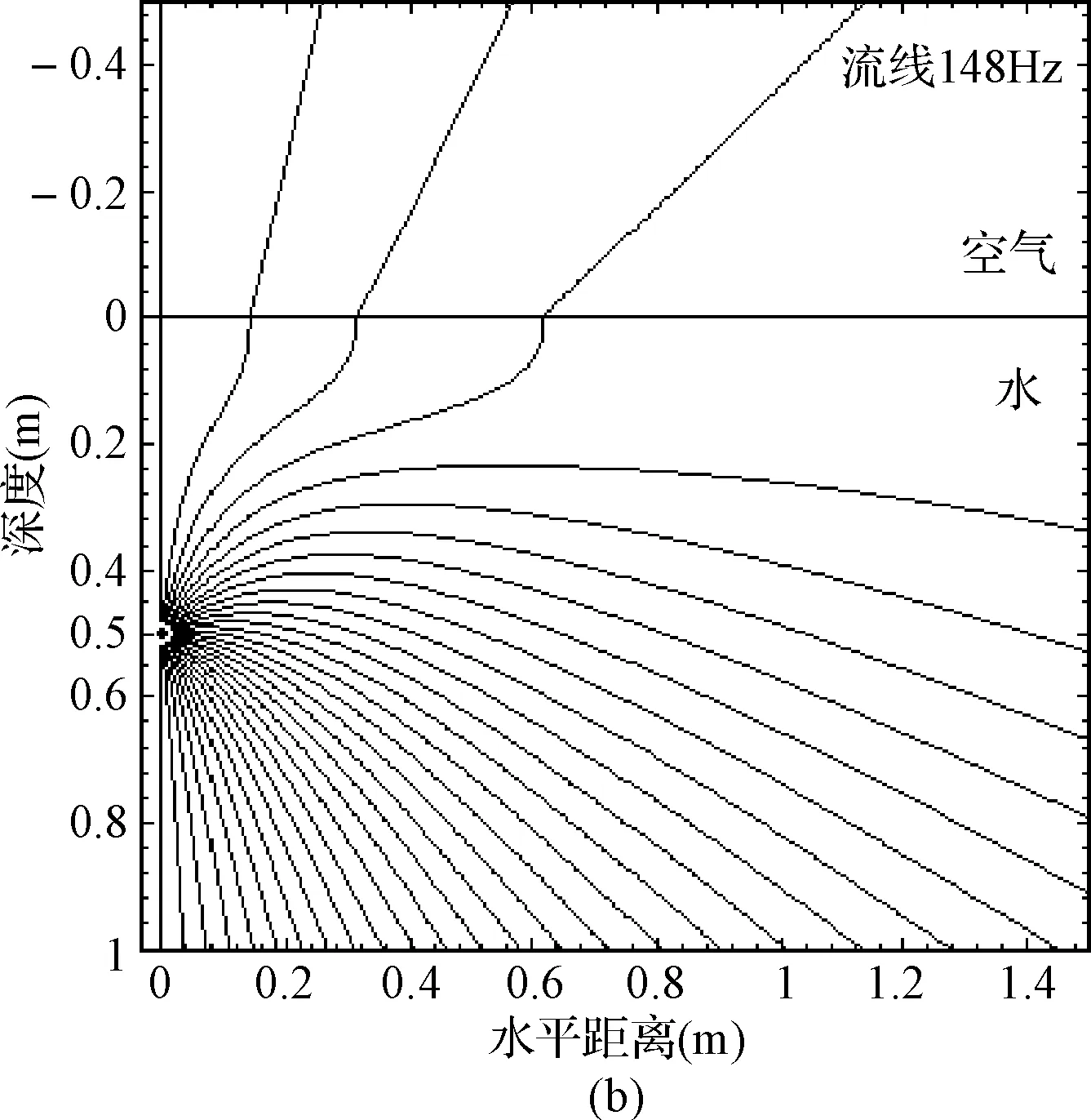


图7 三种频率的声波跨水-空界面传播时的流线图及射线图比较
4 数值仿真
当声波频率很低或声源深度较小时,射线图无法显示非均匀波对水-空界面声传播过程的影响,而声场流线图(Streamlines)理论上可以描述任何波场[11],所以选用声场流线对声波跨水-空界面传播过程进行仿真研究显得十分必要。
声场流线类似于流体力学中的速度流线,它的每一点上的切线方向都平行于此点的声强矢量方向。由式(10)的声强矢量表达式得到声强在r、z方向的分量:
〈Ir〉=(2ωρ)-1Im(p*∂p/∂r)
〈Iz〉=(2ωρ)-1Im(p*∂p/∂z)
(16)
则平均声强矢量与水平方向的夹角φ=arctan(〈Iz〉/〈Ir〉)。据此可以绘出单极子点声源产生的球面声波跨水-空界面传播时的流线图[12],如图7所示。
流线图7(a)~(c)显示,声源深度一定时,频率越低的声波穿过水-空界面的流线越多,直观地说明了透射进入空气中的声能量随频率的降低而增加的规律。由于射线理论忽略了水下非均匀波的作用,射线图7(d)不随频率变化而改变。
5 结语
深度较浅的单极子点声源产生的低频球面声波在水-空界面传播时,由于非均匀波的影响,导致透射进入空气中的能量显著增强。同时,直达波和界面反射波的干涉作用,使得水下的总声能量亦随频率的变化而改变。本文主要使用波动方法对低频球面声波在水-空界面传播的此类特性进行了研究,并与射线结果进行了比较。对于透射入空气中的能量,频率较低时,波动方法考虑了非均匀波的作用,得到的结果可比射线结果高出十几分贝,随着频率的升高,两者结果趋向一致。水-空界面对于低频声能量的透射性要比高频好得多。而水下的声能量不受非均匀波影响,两种方法得到的结果相似。射线结果是高频时波动结果的近似,后者更符合实际情形。
[1] O. A. Godin. Anomalous Transparency of Water-Air Interface for Low Frequency Sound[J]. Phys. Rev. Lett.,2006,97(16):1643011-1643014
[2] Godin O. A. Transmission of low-frequency sound through the water-to-air interface[J]. Acoust. Phys.,2007,53(3):305-312.
[3] Godin O. A. Transmission of low-frequency sound through the water-to-air interface[J]. Acoust. Phys.,2007,53(3):305-312.
[4] B. E. McDonald, D. C. Calvo. Enhanced Sound Transmission from Water to Air at Low Frequencies[J]. J. Acoust. Soc. Am.,2007,122(6):3159-3161.
[5] O. A. Godin. Low Frequency Sound Transmission through a Gas-Liquid Interface[J]. J. Acoust. Soc. Am.,2008,123(4):1866-1879
[6] Deng Y., Tao J., Qiu X. Sound radiation into air by a point source moving underwater[J]. J. Sound Vib.,2012,331(20):4481-4487.
[7] L. M. Brekhovskikh, Yu. P. Lysanov. Fundamentals of Ocean Acoustics[M]. Berlin: Springer-Verlag,2003:61-100.
[8] 刘伯胜,雷家煜.水声学原理[M].哈尔滨:哈尔滨工程大学出版社,2002.
[9] 杜功焕,朱哲民,龚秀芬.声学基础[M].南京:南京大学出版社,2001.
[10] L. M. Brekhovskikh, O. A. Godin. Acoustics of Layered Media 2: Point Sources and Bounded Beams[M]. 2nd ed. Berlin: Springer-Verlag,1999.
[11] O. A. Godin. Wave Refraction at an Interface: Snell’s Law versus Chapman’s Law[J]. J. Acoust. Soc. Am.,2009,125(4):El117-El122
[12] D. M. F. Chapman. Using Streamlines to Visualize Acoustic Energy Flow across Boundaries[J]. J. Acoust. Soc. Am.,2008,124(1):48-56.
Spherical Sound Transmission Through Water-air Surface at Low Frequency
TAO Zhi1FENG Bo2
(1. Equipment Procurement Center of Navy Equipment Department, Beijng 100071) (2. Shenyang Liaohai Equipment Co., Ltd, Shenyang 110003)
Ray-theoretical calculations predict that the transparency of water-air interface is weak because there is a strong acoustic impedance contrast. Based on the analysis of ray theory, wave theory is applied in this paper to study the spherical sound transmission through water-air interface. Assumed the monopole source is sufficiently shallow, the energy transmitted through the interface dramatically increases with decreasing frequency because of inhomogeneous waves that have been neglected before. At the same time, the energy emitted to water changes with the frequency due to the interference of direct and surface-reflected waves. Ray theory is the approximation of wave theory at high frequency.
water-air interface, homogeneous wave, inhomogeneous wave, interference
2014年11月5日,
2014年12月26日
陶智,男,工程师,研究方向:水声工程。冯博,女,助理工程师,研究方向:水声工程。
TN2
10.3969/j.issn1672-9730.2015.05.037
