反舰导弹机动自适应跟踪算法研究*

王朝曦 吴学铜

(中国船舶重工集团公司华中光电技术研究所 武汉 430233)



反舰导弹机动自适应跟踪算法研究*

王朝曦 吴学铜

(中国船舶重工集团公司华中光电技术研究所 武汉 430233)

针对目前舰艇日益严峻的对空防御形势,为提高舰艇对反舰导弹机动突防的探测跟踪能力,首先阐述了目前反舰导弹的典型机动方式,然后在分析“当前”统计模型算法及其部分改进算法缺陷的基础上,提出了一种新的双参数自适应跟踪算法,并以反舰导弹典型机动为例进行仿真验证。实验结果表明,提出的改进算法自适应能力更强,能有效地提高机动目标的跟踪精度。

反舰导弹; 机动目标跟踪; “当前”统计模型; 自适应跟踪算法

Class Number TP391.9

1 引言

反舰导弹是指用于海上作战,攻击敌方水面舰艇的飞航导弹。从上世纪40年代出现至今,反舰导弹在历次海战中毁伤不少舰艇[1～3],其战功显赫,在现代战争中对水面舰船构成极大威胁。经过70年的发展,反舰导弹性能不断提高,种类也愈显丰富,主要包括舰舰、潜舰、空舰和岸舰四类,多具有射程远,命中率高且威力大的特点。加强对反舰导弹的防御对于提高舰艇的生存能力至关重要。

2 反舰导弹机动模型

总体来看,反舰导弹的攻击过程一般包括发射升空、低空巡航、机动规避、导引修正及末端攻击五个部分,其机动突防主要依靠机动规避(侧向机动或蛇形机动等)和末端机动(采用超低空小角度攻击弹道或跃升俯冲攻击弹道等)两个部分组合完成。例如美国的“捕鲸叉”、“战斧”反舰导弹就具有侧向机动配合跃升俯冲的突防模式,俄罗斯的“白蛉””、“马斯基特”反舰导弹由蛇形机动配合跃升俯冲攻击,法国的“飞鱼”反舰导弹采用可编辑航迹点配合低空小角度攻击,再如德国的“鸬鹚”、以色列的“迦伯列”、英国的“海鹰”以及中国的“鹰击”等均具有类似弹道。综观各类反舰导弹,得出最为典型的机动攻击组合模式,即蛇行机动结合跃升俯冲攻击,其攻击过程由图1直观描述。

图1 反舰导弹典型攻击过程示意图

如图1所示,在蛇形机动段,导弹垂直高度基本不变,在水平方向通过等幅等频的航向舵偏指令来控制导弹飞行,使其弹道呈现“S”型,从运动学角度看,主要体现在水平面内导弹的法向加速度和航向角的往复变化;在跃升俯冲段,机动主要发生在纵向,也就是先在垂直方向上给反舰导弹加力,导弹以一定角度和角速度爬升到一定高度,再依靠惯性达到最高点,然后弹头急速旋转,使导弹转过一定角度后,以较大的俯冲角度俯冲攻击目标[4～5]。

3 “当前”统计模型跟踪算法

目前,已经提出的机动目标跟踪模型主要有Singer模型、Noval模型、Jerk模型以及“当前”统计模型等,其中以我国学者周宏仁提出的“当前”统计模型最为普遍接受并广泛使用[6～9]。从本质上讲,该模型是具有自适应非零均值加速度的Singer模型,但与Singer模型中近似假设不同的是,该模型认为,目标在当前时刻以某一加速度机动时,其在下一瞬时的加速度取值范围是有限的,即只能在“当前”加速度的邻域内,故采用修正的瑞利分布来描述机动加速度的统计特性,其分布随均值变化而变化,方差由均值决定。因此,算法在估计目标状态的同时,还可辨识出机动加速度均值,从而实时地修正加速度分布,并通过方差反馈到下一时刻的滤波增益中,实现闭环自适应跟踪[7]。

(1)

其中,F(k)为系统矩阵,G(k)为输入控制矩阵,即

(2)

(3)

V(k)是离散时间白噪声序列,且其协方差矩阵为

(4)

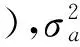
(5)

(6)

目标观测方程为

Z(k)=HX(k)+W(k)

(7)

其中H=[1 0 0],观测噪声协方差R(k)=E[W(k)W′(k)]

由以上给出的状态方程和观测方程,采用“当前”统计模型的跟踪算法为

(8)

4 自适应算法的改进

“当前”统计模型作为目前最为广泛使用的机动目标跟踪模型,在一定程度上解决了机动目标的跟踪问题,但是经仿真实验后可以看出,该模型仍然存在一定的缺陷:其跟踪非机动甚至弱机动的目标时,误差较大;对速度、加速度的估计有明显的时延,跟踪精度不高;对突发机动的跟踪效果不太好等。对其跟踪算法进行分析后发现,造成以上缺陷的主要原因是表征目标机动特性的两个参数—机动频率和机动加速度方差的取值或者调整不当造成,下面分别对其进行分析并加以改进。

4.1 机动频率的自适应算法

在“当前”统计模型中,对机动频率的处理就是根据经验给定一个常值。显然,由于目标的机动状态是不断变化的,使用定值去“一刀切”,对目标的实时机动特性不可能准确描述,此时的状态估计必然会有误差。

选取目标的新息向量的统计特性作为衡量目标机动状况的标准,根据“新息理论”,在滤波过程中,目标的新息向量(残差向量)为

(9)

残差的协方差为

S(k)=HP(k/k-1)HT+R(k)

(10)

距离函数为

D(k)=vT(k)S-1(k)v(k)

(11)

其中,距离函数D(k)服从自由度为m(量测状态数)的卡方分布[10]。

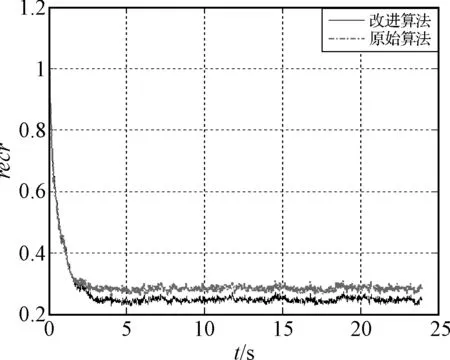
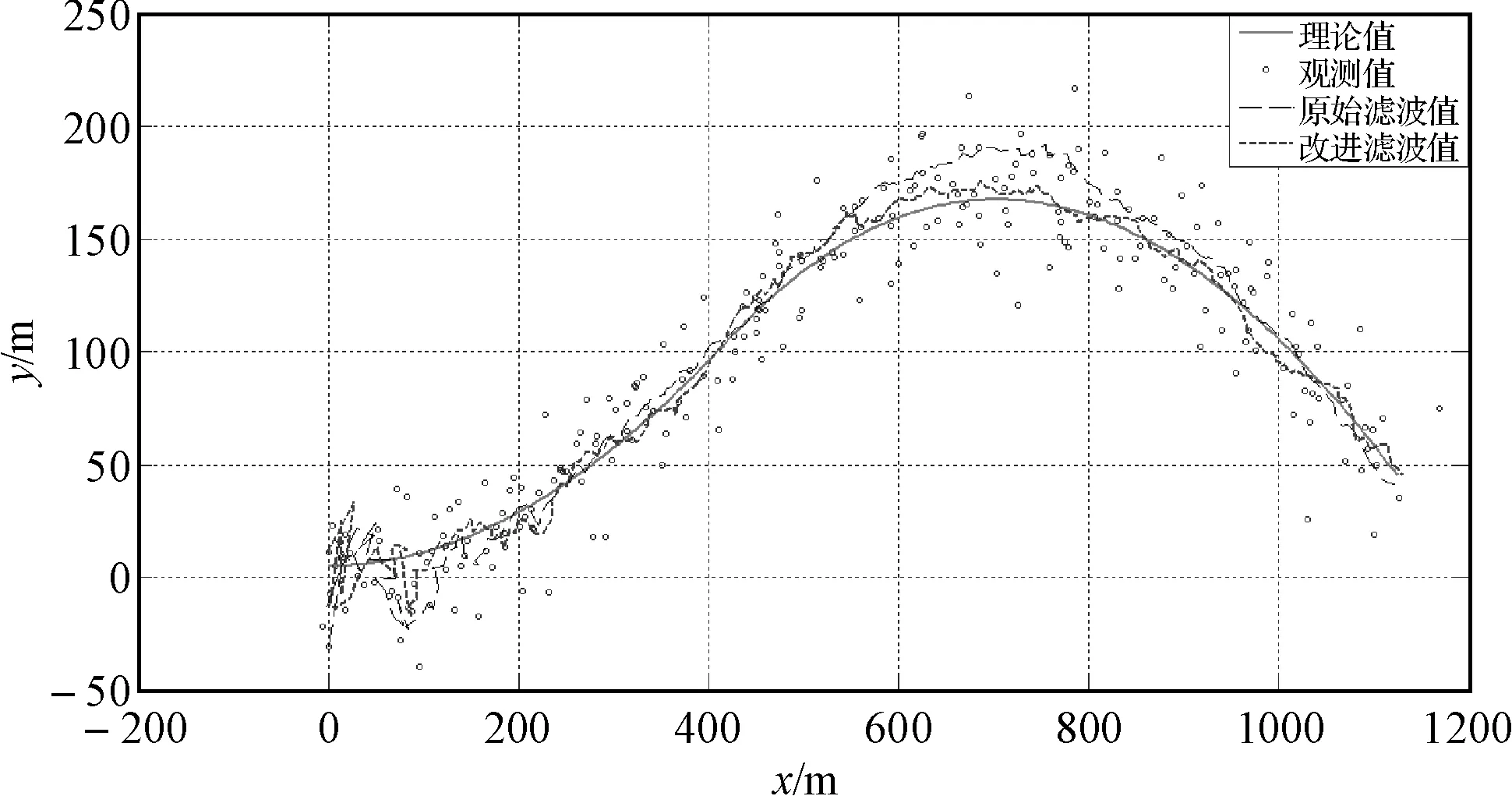
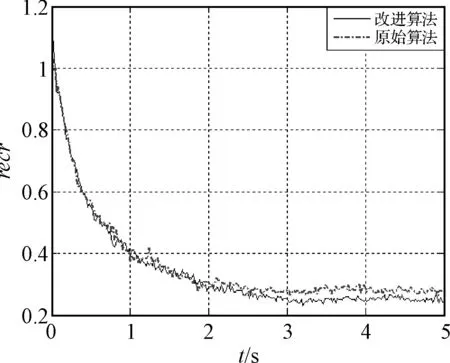
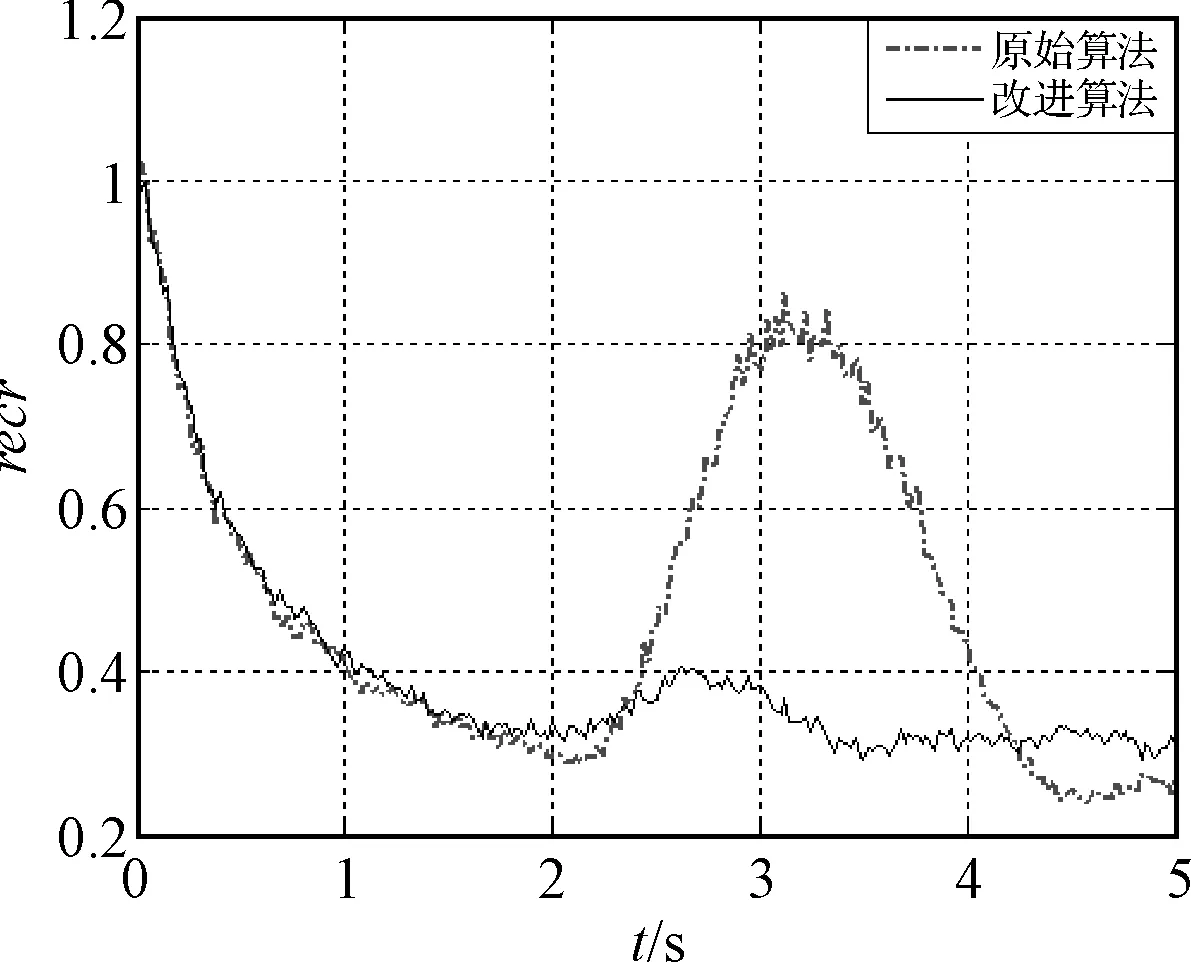
设距离函数的机动阈值为M,当目标发生强机动时,残差向量和距离函数均会变大(D>M),此时应增大α的值;当目标机动减弱时,残差向量和距离函数会变小(D

(12)

其中α0为机动频率初值,D为距离函数,M为机动阈值。

4.2 机动加速度方差的自适应算法

“当前”统计模型算法认为目标机动加速度服从修正的瑞利分布,然而想要以一种先验分布来准确描述机动目标的动态行为,总归是不太合适的。在对原始算法的改进过程中,一些学者仍然只在先验分布基础上进行修正,认为要保持一定的跟踪精度,加速度极限值的选取一般不大,可一旦目标机动加速度超过该值时,其跟踪性能又会明显恶化[11～12,14]。基于这种思想提出的改进算法与原始算法并没有太大的本质区别,例如文献[11]采用截断正态概率密度分布替代原有的分布,实际上不过是将原有的加速度方差自适应算法平方项前面的系数变小了点;还有其它部分文献对加速度极限值进行实时修正[11,14]。这些改进方法或许在一定程度上提高了跟踪精度,但依然没有打破先验分布的桎梏。笔者也对这些改进算法进行了仿真实验,跟踪效果并不太理想。

(13)

状态一步预测的位置分量为

(14)

则有

(15)

即

(16)

由此可以给出一种较为合理的机动加速度方差自适应调整公式:

(17)

其中p为比例系数。

从上式可以看出,当目标机动变强时,位置的估计值与一步预测值之差会变大,使得下一时刻机动加速度方差增大,而且机动越强,方差越大;当目标机动变弱时,位置的估计值与一步预测值之差会变小,使得机动加速度方差减小。因而该算法能较好地反映目标的机动强弱状况,也不用设置任何有关目标运动特性的先验参数,所以具有较高的实用价值。

5 仿真实验

5.1 仿真条件

为验证所提改进算法的有效性,以反舰导弹的典型机动为例,将本文给出的参数自适应算法与原始“当前”统计模型算法进行比较,采用Monte Carlo仿真实验方法对算法的目标跟踪性能进行检验。

仿真条件1:蛇形机动。由于作蛇形机动时导弹高度不变,为简化分析,仿真只在二维直角坐标系xoy中进行。考虑到反舰导弹为时敏目标,并且在实际运动中存在舰体摇摆,导弹轨迹自身的调整以及两者相对运动造成的伪机动等多种影响因素,选取变幅值变周期的非规则准正弦函数作为导弹蛇形机动的近似轨迹。令反舰导弹来回往复的蛇形机动仅表现在纵向(y轴方向),横向(x轴方向)上作初速度为200m/s,加速度为3g匀加速直线运动。另设采样周期0.02s,仿真时间为24s,量测噪声协方差400m2。

仿真条件2:跃升俯冲。同样为简化分析,仿真只在二维直角坐标系xoy中进行,y轴表示导弹垂直高度,x轴表示水平距离。y方向上,在0s～2s内,机动加速度为5g,作跃升;在2s～5s内,机动加速度为-8g,继续跃升到最高点后作俯冲。x方向上作初速度为200m/s,加速度为1g匀加速直线运动。此时采样周期0.02s,仿真时间为5s,量测噪声协方差400m2。

5.2 效果评估指标

进行Monte Carlo仿真实验可得均方根误差RMSE及其平均值RMSE_av:

(18)

(19)

相对误差压缩比recr及其平均值recr_av:

(20)

(21)

5.3 仿真结果及分析

在原始算法中,机动频率取为1/20,机动加速度极限值为15G;改进算法中取机动频率初值为1/20,机动阈值为3,使其强机动概率处在0.1水平;机动加速度方差算法中比例系数取1。分别对两种模型自适应算法进行1000次的Monte Carlo仿真实验,仿真结果如下所示:

1) 仿真条件1—蛇形机动:

仿真结果为:原始算法在x方向和y方向上的均方根误差平均值与相对误差压缩比平均值分别为6.0185,0.3012和14.2401,0.7127;而改进算法在x方向和y方向上的均方根误差平均值与相对误差压缩比平均值分别为5.3454,0.2672和6.7589,0.3381。由此可见,新的自适应算法相比原始算法提高了跟踪精度,而且改进效果明显。

图2 原始算法与改进算法的跟踪效果比较

图3 x方向相对误差压缩比

图4 y方向相对误差压缩比

2) 仿真条件2—跃升俯冲:

仿真结果为:原始算法在x方向和y方向上的均方根误差平均值与相对误差压缩比平均值分别为7.2366,0.3622和9.6715,0.4845;而改进算法在x方向和y方向上的均方根误差平均值与相对误差压缩比平均值分别为6.9002,0.3460和7.9120,0.3960。由此可见,在诸如跟踪匀加速运动的弱机动目标时,新的自适应算法相比原始算法改进效果一般,可一旦出现目标采取突然大机动(比如此时过载发生大幅度阶跃变化)的情况,新的自适应算法能很快调整参数,跟踪滞后比原始算法小得多,跟踪效果更好(如图7所示)。

图5 原始算法与改进算法的跟踪效果比较

图6 x方向相对误差压缩比

图7 y方向相对误差压缩比

6 结语

本文论述了反舰导弹典型机动攻击弹道的特点,在分析“当前”统计模型算法及其部分改进算法缺陷的基础上,提出了一种新的双参数自适应跟踪算法,并以反舰导弹的典型机动为例进行仿真,显示出了改进算法分别在时敏目标机动加速度发生连续变化和大幅度阶跃变化的机动情况下跟踪目标的优势。新的改进算法实现了目标机动强弱的判别,机动频率得以实时调整,并使机动加速度方差的自适应算法避开了先验分布的限制,提高了机动模型与目标实际机动状态的匹配程度,从而提高了对机动目标的跟踪精度。经改进后的参数自适应算法还具有一定的普适性,对于反舰导弹的其它机动动作或其它时敏目标的复杂机动动作(如战斗机的大S机动、筋斗等)跟踪算法的研究也有一定的参考价值。

[1] 袁健全,田锦昌.飞航导弹[M].北京:国防工业出版社,2013:120-129.

[2] 赵育善,吴斌.导弹引论[M].西安:西北工业大学出版社,2006:108-109.

[3] 方有培,汪立萍,赵霜.反舰导弹突防技术研究[J].航天电子对抗,2004(6):40-44.

[4] 李鹏,胡炎.反舰导弹典型运动建模与仿真[J].计算机仿真,2010(5):46-48,79.

[5] 刘剑威,吴传利,徐国亮.反舰导弹典型攻击模式及运动仿真研究[J].指挥控制与仿真,2006(5):47-50.

[6] 周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社,1991:10-144.

[7] 何友,修建娟,张晶炜,等.雷达数据处理及应用[M].北京:电子工业出版社,2013:180-188.

[8] 陈勇,董永强.基于“当前”统计模型的模糊自适应滤波算法[J].火力与指挥控制,2010(8):177-179.

[9] 顾雪峰,刘高峰,王华楠.反舰导弹末端机动模型及仿真研究[J].舰船电子工程,2008(3):112-115,181.

[10] Liu Wang-sheng, Li Ya-an. A modified algorithm for maneuvering target based on current statistical model algorithm[C]//IEEE Digital Manufacturing and Automation(ICDMA), 2010 International Conference. Changsha, IEEE,2010,1:46-49.

[11] 汪云,刘昌云,张纳温,等.改进的截断正态概率密度模型自适应滤波算法[J].空军工程大学学报(自然科学版),2013(4):40-43.

[12] Dongxu Zhu, Kai Chen, Wenjian Gen. A new adaptive filtering algorithm based on the current statistical model[C]//IEEE Intelligent Human-Machine Systems and Cybernetics(IHMSC), 2013 5th International Conference. Hangzhou, IEEE,2013,1:3-6.

[13] Fang Qing, Li Chuan. Design of a modified algorithm for maneuvering targets tracking[C]//Radar, 2006. CIE’06. International Conference. Shanghai, IEEE,2006,1:1-5.

[14] 颉凯平,畅仲仁.当前统计模型自适应滤波算法改进[J].科学技术与工程,2013,19:5504-5507.

[15] 王芳,冯新喜,李鸿艳.一种新的自适应滤波算法[J].现代雷达,2003,7(7):33-35.

Research on Maneuvering Adaptive Tracking Algorithm of Anti-ship Missiles

WANG Zhaoxi WU Xuetong

(Huazhong Institute of Optoelectronic Technology of CSIC, Wuhan 430233)

Concerning the serious air defense situation of naval ship currently, this paper is aimed to improve its ability of detecting and tracking maneuvering anti-ship missiles. Firstly the typical maneuvering mode of anti-ship missile is elaborated, and then, based on analyzing the shortage of current statistical model algorithm and part of its improved algorithms, a new double-parameter adaptive algorithm has been put forward. After that, the typical maneuvering target is chosen as a study case to have a simulation and verify the tracking performance. Results show that the new algorithm has better adaptive capability and improves tracking accuracy effectively.

anti-ship missile, maneuvering target tracking, current statistical model, adaptive tracking algorithm

2014年11月7日,

2014年12月25日

王朝曦,男,硕士,研究方向:运动目标跟踪检测技术。吴学铜,男,硕士,高级工程师,研究方向:光电系统总体。

TP391.9

10.3969/j.issn1672-9730.2015.05.010