高速列车运行对软土区桩—网复合地基的动力影响范围
2015-03-13路言杰闫孔明吴金标王志佳
路言杰,闫孔明,吴金标,陈 勋,王志佳
(1.上海铁路局,上海 200071;2.西南交通大学 土木工程学院,四川 成都 610031)
高速列车运行对软土区桩—网复合地基的动力影响范围
路言杰1,闫孔明2,吴金标2,陈 勋1,王志佳2
(1.上海铁路局,上海 200071;2.西南交通大学 土木工程学院,四川 成都 610031)
针对甬台温铁路某段地基结构,通过拟合较合理的列车荷载时程函数,利用Midas/GTS NX软件建立轨道—路堤—桩网复合结构三维动力耦合模型,探讨了软土区复合地基在列车高速行驶过程中,动应力的分布规律以及传播机理。研究结果表明:时速200 km单行列车在路堤顶部的动力影响范围在距离轨道中心3 m之内;单线偏载行驶在路堤底部形成的动力影响范围在左7 m至右5 m之间;表层地基土体的动力影响范围主要集中在路堤范围内;随着深度的增加,影响范围逐渐增大,但是数值逐渐衰减;桩端土体会产生局部动力响应放大现象;竖向动应力衰减主要集中在路堤结构中完成。
桩—网复合地基 软土地基 列车荷载 动力特性分析 Midas/GTS
近年来,我国客运专线铁路建设事业发展迅速。由于列车运行速度高、动力荷载大等原因,列车荷载引起路基结构的动力响应使线路产生病害,影响运行安全。为此,许多研究人员研究讨论了在不同速率的移动荷载作用下地基的动力响应。Grundmann等[1]研究了一个简谐移动荷载作用时和简化列车荷载作用时层状半平面的动力响应;Hung和 Yang[2]研究了由各种列车荷载引起的黏弹性半空间中弹性波,包括集中移动荷载、均匀分布轮载、弹性分布轮载。由于目前国内高速铁路建设运营时间较短,缺乏足够的高铁线路现场试验研究与监测数据,致使研究工作在较大程度上还依赖于数值模拟加半经验公式。
本文采用预应力混凝土管桩与土工格栅组合形成的桩—网复合地基形式加固地基,通过有限元方法建立轨道—路堤—桩网复合地基三维耦合有限元模型,对高速列车荷载作用在复合地基时,路基中竖向应力的横向分布及竖向衰减规律进行研究,以此讨论单行列车对软土地区高速铁路复合地基的动力影响范围。
1 工程概况
本文的研究对象是甬台温客运专线上某段线路,该段线路通过沿海冲击平原上深厚软土区,地基采用预应力混凝土管桩和土工格栅组成的桩—网复合地基加固。参考竣工设计图,具体地层如下:
(1)粉质黏土,灰色,软塑,厚1.2 m;
(2)-1淤泥质粉质黏土,灰色,流塑,厚11.7 m;
(2)-2粉质黏土,灰色,软塑状,厚22.5 m;
(3)-2淤泥质粉质黏土,灰色,流塑状,厚6.2 m;
(4)粉质黏土,饱和,含铁锰质锈斑,厚2.5 m;
(5)粉砂,饱和,灰色,以粉砂为主,局部含有少量砾石,有少量黏性胶结,厚55.9 m。
甬台温客运专线是一条双线电气化铁路,设计时速为200 km(预留250 km时速),实际运营时速最高为200 km。计算断面地面标高为2.2 m,路肩标高为6.6 m,路基总高4.4 m。如图1所示。
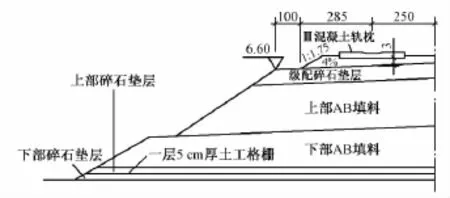
图1 路堤1/2断面(单位:cm)
2 路基动力响应模拟
2.1 材料本构模型及计算参数
在高速列车动荷载作用下,轨道结构一般处于弹性工作状态,所以在进行数值模拟时可采用弹性本构模型,对于路基和路堤材料,需要考虑其塑性特性,则采用弹塑性本构模型进行模拟。在弹塑性模型中,应变分为弹性应变和塑性应变两部分,弹性应变可由广义胡克定理计算,塑性应变则由塑性理论计算。本文则采用Mohr-Coulomb模型对岩土材料进行模拟。
据相关资料及文献[3],得到材料的Mohr-Coulomb 计算参数的合理取值,如表1。

表1 M-C模型材料的计算参数
预应力混凝土管桩采用弹性模型模拟,型号为PHC-AB-500(100),强度≥C80,桩长42.5 m,间距为2.3 m,共13根。外径为0.5 m,内径0.4 m。
管桩及土工格栅计算参数见表2。
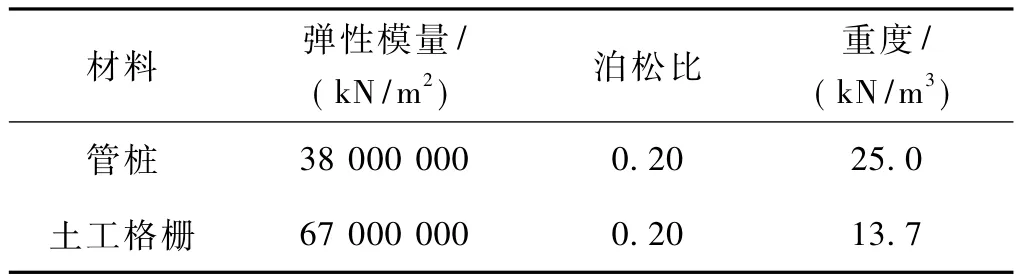
表2 弹性模型材料的计算参数
模型中桩是由梁单元加接触的方法进行模拟。由于桩处于软土地基中,软土性质相差不大,所以简化桩土接触沿全长均相等。桩土接触数值采用经验公式计算。具体为

其中:tv是用来计算接触单元的虚拟厚度,取值为0.1~1.0,默认为0.5;E土为土体的弹性模量。
综上,建立有限元模型如图2所示。
2.2 人工边界
在动力有限元计算中,由于建立的模型尺寸受限,而振动波由上部结构传到复合地基中,模型边界会将振动波在模型中不断反射,使得模型范围内的计算结果失真。对此,为了在有限元动力计算中模拟无限土体,本文采用人工边界模拟波动在模型边界的传播状态[4]。

图2 三维有限元模型
本模型采用线性直接积分法,所以需要模型第1,2振型的周期,即在计算模型动力响应之前要先计算其特征值,然而特征值分析和动力响应分析的人工边界不同。
2.2.1 特征值分析
为了进行特征值分析利用弹性边界来定义边界条件,利用曲面弹簧来定义弹性边界,然后利用铁路设计规范的地基反力系数计算弹簧常量。


式中:kv和kh分别为竖直反力系数和水平反力系数,计算中分别对应Bv与Av和Bh与Ah,Av和Bv分别为地基的竖直方向的截面积和水平方向的截面积;E0为地基的弹性模量;α为经验系数,取值为1.0。
特征值计算得出第1,2振型的周期分别是5.13 s和4.64 s。
2.2.2 动力响应分析
为模拟列车移动荷载的动力分析,需要建立黏弹性人工边界。此模型利用吸收边界代替弹簧来定义边界条件。模型中黏弹性边界的定义是在相应的地基特性值的x,y,z方向输入阻尼。计算阻尼的公式

2.3 列车荷载函数
轮载力的取值是否合理对模型结果有很大的影响。轮载力与列车轴重、轨道形式、行驶速度以及轨道的不平顺性等有关,本模型主要研究的是复合地基的动力响应,即主要是基床底面以下的软土地基,所以在拟合列车荷载函数时,主要侧重于考虑列车轴重与行驶速度的影响。本模型采用设置不同节点动荷载的到达时间来模拟列车运行过程,其中轮载力采用半正弦波模拟。结合与本段线路情况相近的客运专线实测值,拟合得到列车最大轮载力与速度的经验关系式:
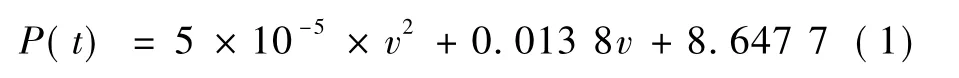
本模型采用上海铁路局的CRH380AL动车组来模拟,模拟时速为200 km。利用上文所得的经验公式计算所得200 km时速对应的最大轮载力为13.407 7 t,即134.077 kN。结合CRH3型动车尺寸[5],采用半正弦波模拟出列车轮载函数,如图3所示。
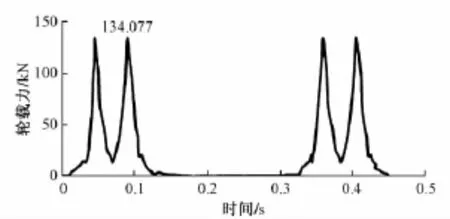
图3 200 km/h下一节车厢的轮载荷载函数
2.4 动力响应计算结果及分析
地理信息系统在测绘当中进行应用,不仅仅可以对地理信息进行采集,还能够对所提取数据信息进行有效储存。与此同时,通过该系统,还可以根据不同地形特征、地理信息等内容构建出与之相对应的信息模型,在充分发挥计算机计算功能基础上,可以得出相应计算结果,这也为后期开展测绘测量工作奠定坚实基础。除此之外,计算结果也能够发挥数据参考作用,确保测绘结果准确和有效。
为了研究动力响应在路堤里面的影响范围,探讨动力响应在横向的分布,现就竖向动应力在不同深度处的横向分布情况作对比分析。以下各层的竖向动应力峰值在横断面的分布均以上行线中点向下的垂线为中心,向左(上行线方向)为负,向右(下行线方向)为正,绘制出曲线图。
1)路堤中竖向动应力在横向的分布
基床表层是路堤结构的顶面,其在列车动荷载作用下产生的动力响应对整个结构而言相当重要,基床表层的动力响应也是整个路堤结构中最大的。基床底层是路堤褥垫层位置处,此处的动应力分布情况对褥垫层的受力和下部地基中桩土动力响应影响较大。本模型中的测点均位于模型纵向的中间断面,提取出各个单元的竖向动应力峰值,绘制出竖向动应力峰值在线路横断面上的分布,如图4所示。

图4 路堤表层和底层竖向动应力峰值的横向分布
从图4中可以发现基床表层竖向动应力的影响范围大概为上行线两侧3 m左右,中间较大两边趋于0,即基床表层的动力波影响范围在其设计宽度范围内。此外,图4曲线上在上行线左右1.3 m处出现波动,这是由于轨枕的影响,轨枕长2.6 m,该两点刚好处于轨枕两端位置下方。
基床底层动力影响范围为上行线左7 m至右5 m内,竖向动应力峰值在线路横向分布不对称,即左侧动应力峰值稍微大于右侧,这是由于列车行驶在上行线,对路堤施加偏载所致。
经过路堤的动力扩散与衰减,相比于基床表层基床底层的竖向影响范围较大,但是数值较小且比较均匀,这对褥垫层土工格栅和地基桩土受力是比较有利的。
2)地基土层竖向动应力在横向的分布
为了探讨地基土体受列车荷载的动力影响,提取地基土层竖向动应力在线路横向的分布,本文将不同深度处的分布曲线绘制在同一张图中进行对比分析。
图5是不同深度处地基土层的竖向动应力峰值横向分布曲线,深度范围取0(桩顶位置处)到45 m(地基底层土体表层)。从图5可以看出不同深度处土层中的竖向动应力横向分布规律基本一致,均为中间大、两边小的趋势。仔细对比分析会发现:①在路堤影响范围内,随着土层深度的增加,竖向动应力峰值总体上减小,只是在桩端位置处局部增大,这是因为动应力波在土层中发生明显的衰减,而传到桩端处时,受桩端动应力的影响,出现了局部增大,之后会再次衰减的,这与图6中竖向动应力峰值在地基中的衰减规律一致;②在路堤影响范围外,随着土层深度的增加,竖向动应力峰值却增大,这是因为应力波传到地基土层中,在深度方向扩散的同时也在横向发生扩散,随着深度的增加,横向影响范围越来越大;③h=42.25 m深度处,横向分布曲线在路堤影响范围内出现等间距波动,这是由于该处土体受桩端的影响,每个桩端均对应一个波峰。
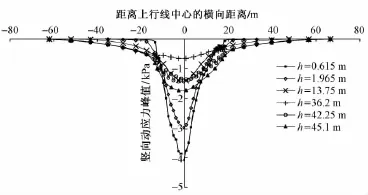
图5 不同深度地基土层的竖向动应力峰值横向分布
3)竖向动应力在深度方向上衰减
列车在高速运行过程中产生的动荷载波动在路堤和地基中产生扩散并衰减,其中竖向动应力的衰减对路基研究相当重要,因为土层中竖向动应力对其竖向变形影响较大,所以路基结构的应力衰减特性直接关系着地基动应力沉降。下面就提取从路堤顶面到地基底层各层土体的竖向动应力峰值,绘制出路基结构竖向动应力在深度方向上的衰减曲线,如图6所示。

图6 路基内竖向动应力峰值在深度方向的衰减
从图6可以发现竖向动应力在深度上总体呈现衰减趋势,只是在不同深度处的衰减率不同。在距离基床表层4 m范围内,衰减率较大,应力衰减较快;超过6 m后,衰减率明显减小。这是由于材料刚度不同的原因,基床表层下4 m范围内的刚度较大,相应地应力衰减也较快。此外,在图6中衰减曲线上存在2个明显的突变点,即发生在4.2 m深度处和44 m到48 m深度处。在4.2 m深度处恰好是处于桩顶处,由于从路基底层到桩顶处,桩顶和褥垫层共同作用,刚度变化较大,所以会存在竖向动应力波动。同时,在路堤底层下2 m范围内(即4 m到6 m范围内)衰减率依然较大,这是由于第一层土的刚度比下面淤泥层的大,且受桩顶的动力影响。在44 m到48 m范围内,动应力突然增大然后又减小,这是由于此处为桩端持力层影响范围内的土层,刚度变大,且受桩端动应力的影响。但是增大不是特别明显,这是因为本模型中桩的类型为摩擦桩,即桩身竖向动应力在桩身深度方向上衰减较明显,传到桩端的竖向动应力较小。
3 结论
1)时速200 km单行列车在路堤顶部的动力影响范围在距离轨道中心3 m之内;这种单线偏载在路堤底部形成的动力影响范围为左7 m至右5 m之间。
2)表层地基土体的动力影响范围主要集中在路堤范围内;随着深度的增加,影响范围逐渐增大,但是数值逐渐衰减。
3)桩端附近的地基土体会产生动力响应局部放大现象,影响桩端土体的承载能力和工作状态。
4)动应力衰减主要集中在路堤结构中完成,以此保证地基结构受动力影响较小。
[1]GRUNDMANN H,LIEB M,TROMMER E.The Response of a Layered Half-space to Traffic Loads Moving along Its Surface[J].Archive of Applied Mechanics,1999(69):55-67.
[2]HUNG H H,YANG Y B.Elastic Waves in Visco-elastic Halfspace Generated by Various Vehicle Loads[J].Soil Dynamics Earthquake Engineering,2001(21):1-17.
[3]中华人民共和国铁道部.铁建设函[2003]439号 新建时速200公里客货共线铁路设计暂行规定[S].北京:中国铁道出版社,2005.
[4]刘晶波,吕彦东.结构—地基动力相互作用问题分析的一种直接方法[J].土木工程学报,1998(3):55-64.
[5]徐进.高速铁路路基模型试验系统研究与动力分析[D].长沙:中南大学,2012.
(责任审编 孟庆伶)
U213.1+5
:ADOI:10.3969/j.issn.1003-1995.2015.11.19
2015-06-23;
:2015-09-08
路言杰(1979— ),男,高级工程师。
1003-1995(2015)11-0061-04
