小型制导炸弹的质量质心计算方法

王明　张美丽　袁宴波

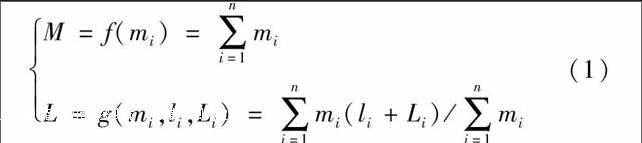
摘要：为掌握小型制导炸弹全弹质量和轴向质心的变化范围，应用合力投影定理和合力矩定理，得出全弹质量质心函数方程，分析了极值法和蒙特卡罗法计算质量质心偏差的可行性，并通过蒙特卡罗法对小型制导炸弹的质量质心进行计算。分析和计算结果表明，采用极值法求解质心偏差最大值的难度较大，而蒙特卡罗法基于各参数在偏差范围内呈正态概率分布，能够更真实地描述全弹质量质心的偏差范围。

关键词：小型制导炸弹；质量计算；质心计算；蒙特卡罗法

中图分类号：TJ760，3：TJ414 文献标识码：A 文章编号：1673-5048（2014）02-0016-03

0、引言

小型制导炸弹以其重量轻、体积小、成本低、作战效能高的特点，逐渐得到了世界各国的广泛关注。相对于500公斤级和250公斤级制导炸弹，小型制导炸弹的战斗部威力较小，需要较高的制导精度才能实现其作战能力。

质量和质心作为小型制导炸弹的基本物理特性参数，是控制系统设计的重要输入。通常，在研制初期，通过全弹质量质心的估算为控制系统设计提供原始输入；在研制末期，控制系统的修正则通过整弹物理样机质量质心的实际测量实现，而受物理样机样本数量的限制，不能真实地获取制导炸弹产品质量质心的变化范围，仍需要根据各组件的实际状态进行全弹质量质心的计算。因此全弹质量质心的计算贯穿于整个研制阶段，质量质心偏差的计算精度则直接影响到控制系统的制导精度。

1、全弹质量质心偏差计算方法

1.1 全弹质量质心函数方程

本文以某小型制导炸弹结构布局方案为例，建立其全弹质量质心方程。

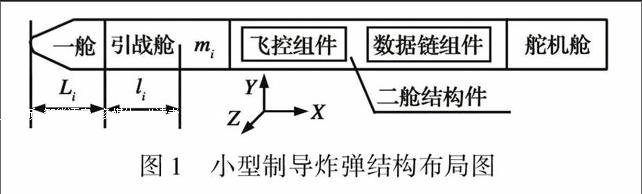
方案中，该小型制导炸弹主要由一舱、引战舱、飞控组件、二舱结构件、数据链组件和舵机舱等部分组成，如图1所示。其中，一舱、引战舱和舵机舱为单独形成舱段的组件：二舱结构件包含舱段壳体、内部支架和外部翼面等零件；飞控组件和数据链组件则安装于二舱舱段壳体内部。

如图1所示，可假设：

a.沿x轴正方向，各组件的质量依次为m₁，m₂，…，m_n；

b.沿x轴正方向，各组件质心在x轴的投影距离本组件前端面的距离依次为l₁，l₂，…，l_n；

c，沿x轴正方向，各组件前端面距离弹体前端面的距离依次为L₁，L₂，…，L_n。

通过上述参数假设，根据合力投影定理和合力矩定理，可得出全弹的质量质心函数方程：式中：M和L分别为全弹的质量和轴向质心位置。

1.2 质量质心偏差产生的原因

在各组件的装配过程中，结构零件的加工误差、元器件的制造误差和辅助性材料的非定量使用，均会导致组件的质量质心偏离设计值。

全弹在总体装配过程中，各舱段间的连接误差和舱段内相关组件的安装误差均会影响全弹质量质心的偏移量。

综上，全弹质量质心发生偏差的主要因素有各组件的质量质心偏差、各舱段间的连接误差和舱段内相关组件的安装误差。

通常，各组件的质量质心偏差量可由组件研制任务书或设计人员提供：舱段连接误差和舱段内组件的安装误差可由总体结构设计人员提供。

目前，根据公式（1），计算全弹质量质心最大偏差AM，AL的方法可选择极值法和蒙特卡罗法。

1.3 极值法计算质量质心偏差

极值法通过采用极端假设的方式可以将某些多元函数问题简单化，是一种重要的数学思想和分析方法。

对于公式（1）中的f（m_i）函数，m_i均取最大值时，即可求得

式中：△m_i为沿x轴正方向，第i个组件的质量偏差最大值。

对于公式（1）中的g（m_i，l_i，L_i）函数，分子取最大值时，需m_i，l_i，L_i均取最大值，此时函数分母也相应变化为最大值。两最大值相除不能判断其结果的最值，因此，无法确定g（m_i，l_i，L_i）函数的最值。可见，极值法可以有效地计算出全弹质量偏差最大值，但不能计算出全弹质心偏差最大值。

1.4 蒙特卡罗法计算质量质心偏差

蒙特卡罗法又称统计模拟法、随机抽样技术，是一种随机模拟方法，是以概率和统计理论方法为基础的一种计算方法，是使用随机数或伪随机数来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系，用计算机实现统计模拟或抽样，以获得问题的近似解。

蒙特卡罗法计算全弹质量质心偏差的过程可分为三个步骤：

a.确定各变量的分布函数。通过前面的分析可知，影响m_i，l_i，L_i的因素主要为结构零件的加工误差、元器件的制造误差和辅助性材料的非定量使用。实际工程计算过程中，上述因素可视为相互独立，且分布函数服从正态分布，因此可认为m_i，l_i，L_i，f（m_i）和g（m_i，l_i，L_i）的分布函数同样服从正态分布。

b.产生随机数并抽样。蒙特卡罗法需要大量的样本，因此可在（0，1）区间内产生大量的服从均匀分布的随机数，并将其转换为服从正态分布的m_i，l_i，L_i样本。

c.将抽样样本代入公式（1）计算，并统计计算结果。通过计算，可以获得大量的全弹质量和质心数据，对其进行统计分析可以得到均值、方差等统计量，最后对结果进行评判分析。

综上，蒙特卡罗法能够模拟全弹质量质心偏差的近似解，并且随着抽样次数的增加，求解精度逐渐提高。

2、蒙特卡罗法计算实例

以某小型制导炸弹方案为例，通过在MAT-LAB软件中编译程序，可以实现全弹质量质心偏差的蒙特卡罗法计算，其程序计算的流程图如图2所示，相关计算参数如表1所示。

选取5000，10000，20000，50000，100000和200000等6种抽样次数对全弹质量质心进行仿真计算。计算结果见表2。

表2中，μ为数学期望，即为各统计样本值的平均值，σ²为方差，即为各统计样本值相对于μ的离散程度。对于正态分布函数，可以认为，各统计样本是以999937%的概率位于（μ-4σ，μ+4σ）之间。

由表2可知，当抽样次数达到50000次时，计算精度已经能够满足方案要求，并且全弹质量以99.9937%的概率位于（118.29，121.71）kg之间，全弹质心以99.9937%的概率位于（996.2，1020.4）mm之间，可以认为通过蒙特卡罗法获得的全弹质量为120±1.71 kg，全弹质心为1008.3±12.1 mm。

将m_i，f_i，L_i值分别代入公式（1）和（2），可获得全弹质量理论值为120 kg、全弹质心理论值为1008.3 mm以及全弹质量偏差最大值的极值法解为2.55 kg。

通过对比可知，采用极值法计算得到的全弹质量偏差最大值近于小概率事件，而蒙特卡罗法更符合实际情况。

通过上述方法，可在方案研制初期，根据计算结果合理地调整、分配各组件的质量质心偏差和舱段壳体零件的公差，使其满足给定的全弹质量质心范围要求。

3、结论

为掌握全弹质量和轴向质心的变化范围，本文对某小型制导炸弹结构布局方案进行了研究：建立了全弹质量质心函数方程，分析了极值法和蒙特卡罗法计算质量质心偏差的可行性，并进行了实例计算。通过分析和计算，可以得到如下结论：

（1）极值法可以有效地计算出全弹质量偏差最大值，但不能计算出全弹质心偏差最大值；

（2）极值法计算的全弹质量偏差最大值近于小概率事件，难以反映客观实际：

（3）蒙特卡罗法作为一种统计试验方法，基于各参数在偏差范围内呈正态概率分布的事实，能够更真实地描述全弹质量质心的偏差范围：

（4）在小型制导炸弹的方案研制初期，可以根据蒙特卡罗法的计算结果合理地调整、分配各组件的质量质心偏差和舱段壳体零件的公差，使其满足给定的全弹质量质心范围要求。