基于状态重构的吸气式高超声速飞行器鲁棒反演控制

卜祥伟，吴晓燕，马 震，张 蕊

(空军工程大学 防空反导学院，西安 710051)



基于状态重构的吸气式高超声速飞行器鲁棒反演控制

卜祥伟，吴晓燕，马 震，张 蕊

(空军工程大学 防空反导学院，西安 710051)

针对吸气式高超声速飞行器参数不确定弹性体模型，仅考虑速度、高度和俯仰角速度可测的情况，提出了一种基于状态重构的鲁棒反演控制器设计方法。首先，将被控对象模型表示为严格反馈形式，分别采用动态逆和反演设计实际控制律和虚拟控制律；其次，引入反正切跟踪微分器来简化虚拟控制律求导运算，并用于对弹道角和攻角进行状态重构；最后，为了保证反演控制器的鲁棒性，基于非线性-线性跟踪微分器，设计了一种新型非线性干扰观测器，可实现对模型不确定项的精确估计和补偿。仿真结果表明，所提策略取得了较高的状态重构精度，控制器能够克服模型不确定项的影响，且能保证速度和高度对参考输入的稳定跟踪。

吸气式高超声速飞行器；鲁棒反演控制器；反正切跟踪微分器；状态重构；非线性-线性跟踪微分器；非线性干扰观测器

0 引言

吸气式高超声速飞行器动力学的高不确定性主要源于3个方面[1-3]：一是飞行器气动推进结构耦合关系复杂，尚未建立完善的风洞试验和飞行实测数据库；二是柔性材料的大量使用导致其细长体机身在大马赫数飞行时极易发生弹性变形，气动加热效应则进一步加剧了飞行器弹性状态与刚体状态的耦合效应；三是大包线飞行过程中飞行器容易受到各种大气干扰。这使得高超声速飞行器控制系统设计面临着前所未有的挑战。

对于参数不确定问题，传统思路是采用自适应或鲁棒控制技术。文献[4]采用输出反馈策略，设计了一种线性鲁棒控制器。文献[5]基于特征模型设计了一种自适应控制器。文献[6]设计了一种自适应高阶滑模控制器。但鲁棒控制过于保守，自适应控制存在参数漂移现象。通过设计干扰观测器，对模型不确定项进行有效估计和补偿，已经成为解决模型参数不确定问题的有力手段。文献[7]设计了一种鲁棒滑模观测器，可实现对模型不确定项和未知扰动的在线估计，但观测输出存在弱抖振。文献[8]设计了一种滑模反演控制器，并设计非线性干扰观测器用于对模型不确定项进行补偿和削弱滑模控制输出抖振，但其观测器是基于未知扰动的一阶导数为零的假设而设计的，这与实际情况并不相符。文献[9]基于高阶滑模微分器，设计了一种新型非线性干扰观测器，但仍存在输出抖振和参数整定困难的问题。以上研究都假设所有状态是精确可测的，可对于吸气式高超声速飞行器这类弹性体飞行器，高速飞行时，严重的气动加热效应和显著的弹性振动，导致攻角和弹道角等小角度值的测量变得极为困难；同时，弹性状态又是不可测量的。因此，考虑弹道角和攻角不可测时的控制策略研究，具有重要的工程实践意义。

本文将研究部分状态不可测时的鲁棒反演控制器设计问题。首先，引入反正切跟踪微分器，利用可测状态速度、高度和俯仰角速度，对弹道角和攻角进行精确重构；其次，基于重构以后状态进行反演控制器设计，并采用反正切跟踪微分器简化虚拟控制量的求导运算；而后，基于高稳快速非线性-线性跟踪微分器，设计一种新型非线性干扰观测器，可实现对模型不确定项的平滑估计，并可解决弹性状态不可测的问题。最后，通过实例仿真来验证控制策略的有效性。

1 吸气式高超声速飞行器运动学模型

通用的吸气式高超声速飞行器纵向运动学方程可描述为

(1)

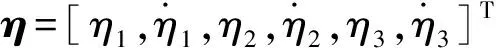
模型(1)中的推力T、阻力D、升力L和俯仰力矩M以及广义弹性力Ni(i=1,2,3)拟合形式如下:

(2)

式(1)和式(2)中的飞行器参数和详细气动参数见文献[10]。由式(1)和式(2)易知，刚体状态和弹性状态通过气动力T、D、L、M和广义弹性力Ni(i=1,2,3)构成严重的耦合效应。因此，控制系统的任务除了保证刚体状态稳定跟踪参考输入之外，还必须得有效抑制机体弹性振动。

(3)

则模型(1)可转化为如下严格反馈形式：

(4)

2 控制器设计

2.1 基于反正切跟踪微分器的状态重构

为了对弹道角和攻角进行重构，先给出以下合理假设和引理。

假设1 刚体状态速度V、高度h和俯仰角速度Q精确可测，且经过滤波处理，即不含量测噪声。

引理1[11]

对于如下系统：

(5)

如果R、a1、l1、a2、l2都为正数，则对任意有界可积函数υ(t)和任意时间常数T>0，则系统(5)的解x1(t)满足：

|x1(t)-σ(t)|dt=0

(6)

即x1(t)平均收敛于σ(t)，x2(t)弱收敛于σ(t)的一阶导数。

下面将利用系统(5)对弹道角γ和攻角α进行精确重构，重构过程如图1所示。

图1 弹道角和攻角重构

考虑到模型(1)中h-子系统是一种精确对应关系，不包含任何不确定性，可利用该式对弹道角γ进行重构：

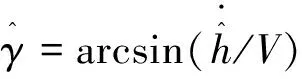
(7)

(8)

利用模型(1)中的α-子系统，经过一次积分可对攻角α进行重构：

(9)

(10)

2.2 基于动态逆的速度控制器设计

将速度跟踪误差定义为

(11)

对式(11)求导，并结合式(4)中V-子系统，可得

(12)

根据动态逆理论，将实际控制量Φ设计为

(13)

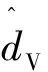
2.3 基于反演的高度控制器设计

将高度、弹道角、攻角和俯仰角速度跟踪误差分别定义为

(14)

对式(14)求导，并结合式(4)中的h、γ、α和Q-子系统，可得

(15)

(16)

(17)

(18)

(19)

由式(17)～式(19)可知，反演设计中要用到虚拟控制量的一阶导数，通常情况下其导数是不易获取的。这里，采用系统(5)对虚拟控制量的一阶导数进行精确估计。

(20)

(21)

(22)

2.4 非线性干扰观测器设计

文献[12]针对传统全程快速跟踪微分器输出伴有明显颤振和设计参数过多的问题，提出了一种新型非线性-线性跟踪微分器。该微分器的非线性部分保证跟踪误差收敛的快速性，线性部分则可有效削弱输出颤振。同时，设计参数较少，且物理意义明确，便于参数整定。其具体形式如下。

引理2[12]

对于如下系统：

(23)

式中b1>0，b2>0，P>0；m为大于2的奇数。

对任意有界可积函数υ(t)和任意时间常数T>0，则系统(23)的解x1(t)满足：

|x1(t)-υ(t)|dt=0

(2)

即x1(t)平均收敛于υ(t)，x2(t)弱收敛于υ(t)的一阶导数。

利用系统(23)可设计一种估计性能优异的新型干扰观测器。对于如下参数不确定系统：

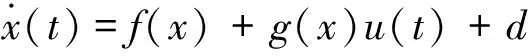
(25)

式中x(t)、u(t)分别状态量和控制量；d为系统不确定项；f(x)、g(x)为已知量。

将非线性干扰观测器设计为

(26)

采用非线性干扰观测(26)，可分别实现对模型不确定项的有效估计。

(27)

(28)

(29)

(30)

2.5 稳定性分析

定义状态重构误差：

(31)

定义虚拟控制量估计误差：

(32)

定义不确定项估计误差：

(33)

由引理1和引理2易知，通过选择合适的设计参数，式(31)～式(33)中的误差都可在有限时间收敛到零。

因此，将Lyapunov函数选为

W=WV+Wh+Wγ+Wα+WQ

(34)

其中

(35)

(36)

(37)

(38)

(39)

对式(35)～式(39)求导，并根据式(11)～式(19)，可得

(40)

考虑到：

则有

(-kQ,1+|gα|/2)Q2

(17)

3 实例仿真

在MALAB/SIMULINK环境下对模型(1)进行闭环系统仿真。考虑典型的等动压巡航飞行状态，取初始平衡状态为V=2 331.7 m/s，h=26 212.8 m，保持q=90 148 Pa不变，速度阶跃值为ΔV=351. 6 m/s，高度阶跃值为Δh=1 828.8 m。考虑到速度和高度阶跃幅值较大，为了避免出现控制量饱和的问题，本文将高度参考输入通过阻尼为0.95、自然频率为0.03 rad/s的二阶参考模型给出[10]。选用四阶RungeKuta法求解，仿真步长选为0.01 s。为了体现控制器的鲁棒性，考虑式(1)～式(2)中的飞行器质量、参考面积、转动惯量和所有气动拟合系数均摄动±30%。通过向V-子系统和Q-子系统分别加入如下时变扰动ΔV=0.46sin(0.01πt) m/s，ΔQ= 1.79sin(0.01πt) °/s来模拟参数摄动；同时，考虑到速度V为较大量，参数摄动对γ和α-子系统的影响较小。控制器设计参数、微分器设计参数和非线性干扰观测器设计参数如表1所示。

表1 控制器、微分器和干扰观测器参数

作为对比，分别在基于真实状态和重构状态进行仿真，仿真结果如图2～图8所示。其中，图2～图5中的下标“1”表示基于真实状态时的仿真结果，下标“2”表示基于重构状态时的仿真结果。从仿真结果可看出，不论是基于真实状态，还是基于重构状态，本文提出的控制策略均能取得很好的控制效果，速度和高度跟踪误差非常小，且能很快收敛到零，由于整个过程中飞行器的姿态角γ、α、Q和控制输入Φ、δe都处在合理的范围内且较平滑，机体弹性振动得到了很好地抑制，能够快速收敛，并逐渐趋于稳定。

图2 速度跟踪曲线和跟踪误差

图3 高度跟踪曲线和跟踪误差

图4 弹道角、攻角和俯仰角速度响应曲线

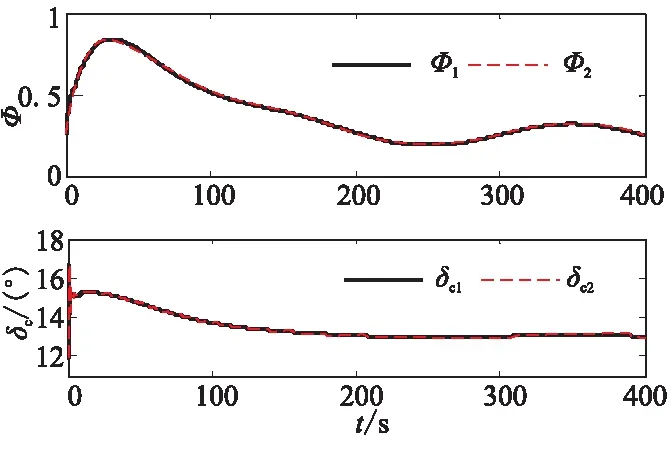
图5 控制输入

图6 弹性状态响应及变化率曲线

图7 模型不确定项估计曲线

图8为状态重构效果图。可知，本文所提策略实现了对弹道角和攻角的高精度重构，重构误差很小，且收敛非常迅速，保证了基于重构状态设计的控制律具有良好的控制效果。

图8 状态重构曲线

4 结论

(1)针对吸气式高超声速飞行器参数不确定和部分状态不可测的控制问题，提出了一种基于状态重构的鲁棒反演控制方法。基于反正切跟踪微分器，对不可测状态进行精确重构，并基于高稳快速非线性-线性跟踪微分器，设计了一种新型非线性干扰观测器，保证了控制器对不确定参数的强鲁棒性。

(2)仿真结果表明，弹道角和攻角重构精度高，非线性干扰观测器可实现对模型不确定项的有效平滑估计，在存在参数不确定时，控制器仍可提供稳定的速度和高度跟踪控制。

[1] 葛东明.临近空间高超声速飞行器鲁棒变增益控制[D].哈尔滨：哈尔滨工业大学,2011.

[2] Lisa Fiorentini,Andrea Serrani.Adaptive restricted trajectory tracking for a non-minimum phase hypersonic vehicle model [J].Automatica,2012,48:1248-1261.

[3] Zong Qun,Wang Jie,Tian Bai-ling,et al.Quasi-continuous high-order sliding mode controller and observer design for flexible hypersonic vehicle[J].Aerospace Science and Technology,2013,27:127-137.

[4] David O Sigthorsson,Pete Jankovsky,Andrea Serrani, et al.Robust linear output feedback control of an airbreathing hypersonic vehicle[J].Journal of Guidance, Control,and Dynamics,2008,31(4):1052-1066.

[5] Zhang Zhao,Hu Jun.Stability analysis of a hypersonic vehicle controlled by the characteristic model based adaptive controller[J].Science China (Information Sciences),2012,55:2243-2256.

[6] Xu Hao-jian,Maj D Mirmirani,Petros A.Ioannou.Adaptive sliding mode control design for a hypersonic flight vehicle[J].Journal of Guidance,Control,and Dynamics,2004,27(5):829-838.

[7] 宋超,赵国荣,陈洁.基于鲁棒滑模观测器的高超声速飞行器双环滑模控制[J].固体火箭技术,2012,35(4):438-441.

[8] 宋超,赵国荣,盖俊峰.基于非线性干扰观测器的高超声速飞行器反演滑模控制[J].系统工程与电子技术,2012,34(6):1231-1234.

[9] Yang Jun,Li Shi-hua,Sun Chang-yin.Nonlinear-disturbance-observer-based robust flight control for airbreathing hypersonic vehicles[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(2):1263-1275.

[10] Lisa Fiorentini.Nonlinear adaptive controller design for air-breathing hypersonic vehicles[D].Columbus：The Ohio State University,2010.

[11] 董小萌,张平.反正切形式跟踪微分器设计及相平面分析[J].控制理论与应用,2010,27(4):533-537.

[12] 赵鹏,姚敏立,陆长捷,等.高稳快速非线性-线性跟踪微分器设计[J].西安交通大学学报,2011,45(8):43-48.

(编辑：吕耀辉)

State-reconstruction-based robust backstepping control of air-breathing hypersonic vehicles

BU Xiang-wei， WU Xiao-yan， MA Zhen， ZHANG Rui

(Air and Missile Defense College， Air Force Engineering University， Xi'an 710051， China)

A robust backstepping controller was designed based on state reconstruction for flexible air-breathing hypersonic vehicles considering that only the velocity,altitude and pitch rate were observable. Firstly,the controlled plant was rewritten as a strict feedback form，and the actual control laws and virtual control laws were designed based on dynamic inversion and backstepping respectively. Secondly,arctangent tracking differentiator was introduced to estimate the derivatives of virtual control laws and reconstruct the states of flight-path angle and angle of attack.Finally,in order to guarantee the backstepping controller' robustness,a new nonlinear disturbance observer was designed based on nonlinear-linear tracking differentiator to estimate and compensate uncertainties of the model precisely.Simulation results show that a high precise state construction can be obtained by the proposed strategy and the presented control methodology can provide a stable altitude and velocity tracking,and eliminate the influence of the uncertainties of the model.

air-breathing hypersonic vehicles;robust backstepping controller;arctangent tracking differentiator;state reconstruction; nonlinear-linear tracking differentiator;nonlinear disturbance observer

2014-04-07；

2014-05-14。

航空科学基金(20130196004)；陕西省自然科学基础研究计划项目(2012JM8020)。

卜祥伟(1987—)，男，博士生，研究方向为飞行器建模与控制。E-mail:buxiangwei1987@126.com

V448

A

1006-2793(2015)03-0314-06

10.7673/j.issn.1006-2793.2015.03.003