月球探测器环月段返回速度影响因素研究

饶建兵 向开恒 彭坤

(1 北京电子工程总体技术研究所， 北京 100854) (2 北京空间技术研制试验中心， 北京 100094)



月球探测器环月段返回速度影响因素研究

饶建兵1向开恒1彭坤2

(1 北京电子工程总体技术研究所， 北京 100854) (2 北京空间技术研制试验中心， 北京 100094)

环月探测器存在需要返回地面的情况，由于环月探测器返回轨道动力学模型的高度非线性，很难从机理上对其进行分析。针对此问题，文章首先建立一种月地转移轨道设计模型，提出了月地转移出发圆的概念，分析并确定了出发圆参数的主要影响因素是返回时间和返回轨道倾角，而后分析了出发圆参数随主要影响因素的变化规律。当返回时间参数N给定时，出发圆具有一定稳定性，基于此分析了恶劣情况下的环月返回机动策略。最后定义Nr作为月球探测器的返回能力量化指标，并给出了不同Nr值对应的速度增量需求。

环月轨道； 返回轨道； 月地转移出发圆

1 引言

月球探测器返回存在从多个位置返回地面的情况，尤其在探测器故障模式中更是如此。探月任务中较为容易发生故障的情况为各次大的轨道机动，造成的故障轨道可能为绕地球的大椭圆轨道[1]、地月转移轨道[2]、逃逸月球轨道[3]和环月轨道，其中，前三者的应急机动机理较为清晰，得到了较为充分的研究，而环月轨道应急返回情况的研究较少。美国“星座”计划中采用自由返回轨道奔月而登月点不在中低纬度，需要执行环月轨道面机动，从而导致故障环月轨道的倾角变化范围较大，在地、月和探测器这样的高度非线性动力学系统中，很难从机理上对环月轨道出发参数变化范围进行分析。

另外，月球探测器的返回能力是任务安全性的重要指标，但却没有可以量化的系统指标对其进行表述。返回探测器最远到达的就是环月轨道，环月返回机动是探测器最后一次大的轨道机动，因而满足环月返回时的能力需求即可达到探测器安全返回的要求。分析环月段返回参数变化规律有助于找到这样一个量化指标对探测器的返回能力进行描述。

本文首先基于约束一端方向角的类Lambert问题求解方法、伪状态理论轨道预报方法和多维截线迭代方法，建立了一种月地转移轨道设计方法。针对环月段返回问题，提出了“月地转移出发圆”的概念，确定了出发圆参数的主要影响因素并分析了出发圆参数变化规律。基于此，定义了系统返回能力参数Nr，给出了不同Nr值对应的速度增量需求。

2 月地转移轨道快速设计模型

月地转移轨道设计模型分三部分：①求解约束一端方向角的类Lambert问题；②基于伪状态方法的轨道预报；③求解满足再入约束的转移轨道。本文着重采用该模型对环月段返回定点着陆轨道进行轨道特性分析，因而只对模型进行简要介绍。

2.1 约束一端方向角的类Lambert问题

针对约束再入角的转移轨道设计问题，对一种基于普适变量法的一般Lambert问题求解方法[4]进行改进，问题描述为：给定转移起始位置r1，转移终点位置r2，飞行时间约束Δttarget和一端速度方向角β1，计算起始点和终止点的速度v1和v2。经论证表明[5]，改变约束后，仍然可以采用普适变量法进行求解，详细求解计算流程参见相关文献[5]。

2.2 基于伪状态方法的轨道预报

伪状态轨道预报方法是基于圆锥曲线重叠法的针对地月空间转移轨道设计的改进，在“阿波罗”飞船登月工程中得到了应用。定义以月球为中心的伪状态球(PTS)，在PTS外只考虑地球引力影响，在PTS内，将地球引力和月球引力解耦考虑，预报流程为[6]：采用地心二体轨道预报方法，从起始点预报到伪状态向量RS终点；从RS终点线性回溯到伪状态球边界；采用月心二体轨道预报方法，从伪状态球边界预报到近月点。

伪状态方法适用于行星和它的远距离大卫星之间的转移轨道设计，不同的系统对应的伪状态球半径不同，地月系统中的伪状态半径取24倍的地球半径[7]。

2.3 满足再入约束的月地转移轨道求解

给定起始点位置向量初值(RS)等于月球位置(Rm)，以惯性空间目标点再入角、返回轨道倾角和再入点经度为自变量X1=[γAiAλA]T，以再入点相对地球的再入角、返回轨道倾角和再入轨道面与着陆场矢量夹角为目标量，取其余弦值，则目标值期望为Fexp=[cosγEcosiE0]T。初始化X1为[γEiEλL]T，λL为着陆场经度。

通过几何分析，求得从RS到达惯性空间目标点的转移时间Δttarget=N+G/we，其中正整数N为指定的转移天数，G=GS+α+β-λA，GS为RS在地固系中的角坐标，α为RSke平面与heke平面之间的夹角，β为RAke平面与heke平面之间的夹角，通过球面三角关系求得。ke为地轴单位矢量，he为返回轨道法向单位矢量，RA为由X确定的惯性空间目标点。分析示意图如图1所示。

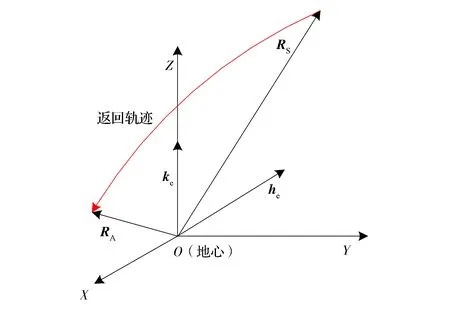
图1 返回时间分析示意图Fig.1 Figure for analysis of return time

由此，即可采用约束一端方向角的类Lambert问题求解方法得到从RS出发并经过惯性空间目标点的轨道，得出再入点相对地球的位置、速度Ref和Vef，计算目标量：

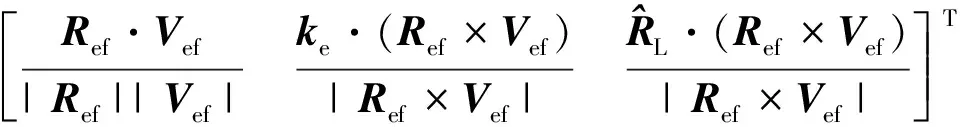
(1)

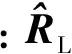
(2)

(3)

式中：ΔXk=Xk-Xk-1，ΔFk=Fk-Fk-1，当k=1时，J1为单位阵。重复以上步骤直到|Fk-Fexp|<ε1，(ε1为小量)求解完毕，输出该满足再入约束的再入点位置和速度。

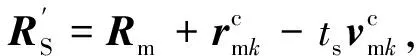
3 定点着陆返回轨道特性分析

3.1 月地转移出发圆概念

在中心天体轨道坐标系下，渐近线相互平行的同一时刻的逃逸双曲线近心点在空间形成一个圆，如图2所示。从该簇双曲线逃逸，无限远处速度方向相同而位置差异很小，可以认为是以相同的状态到达同一个目标位置，因而称该簇双曲线的近心点组成的圆为出发圆，圆上每一个点对应的位置和速度称为该时刻的出发圆参数，由Φ(t)表示。由此可知，无限远速度方向垂直出发圆，出发圆上任意一点位置和速度相互垂直。

在月地转移轨道中，逃逸月球后还未到达无限远即进入地球影响球，但是同样存在月地转移出发圆。首先定义月球轨道坐标系(右手系)：以月心为原点，X轴为地月连线并指向月球方向，Z轴为瞬时白道面正法向。采用月地转移轨道快速设计模型，以相同的再入状态为目标参数，遍历环月轨道倾角0°～180°和升轨、降轨出发方式，可以快速刻画某一时刻的出发圆，如图3所示，图中X轴为月球位置矢量方向，Z轴为白道瞬时正法向，坐标原点在球心。

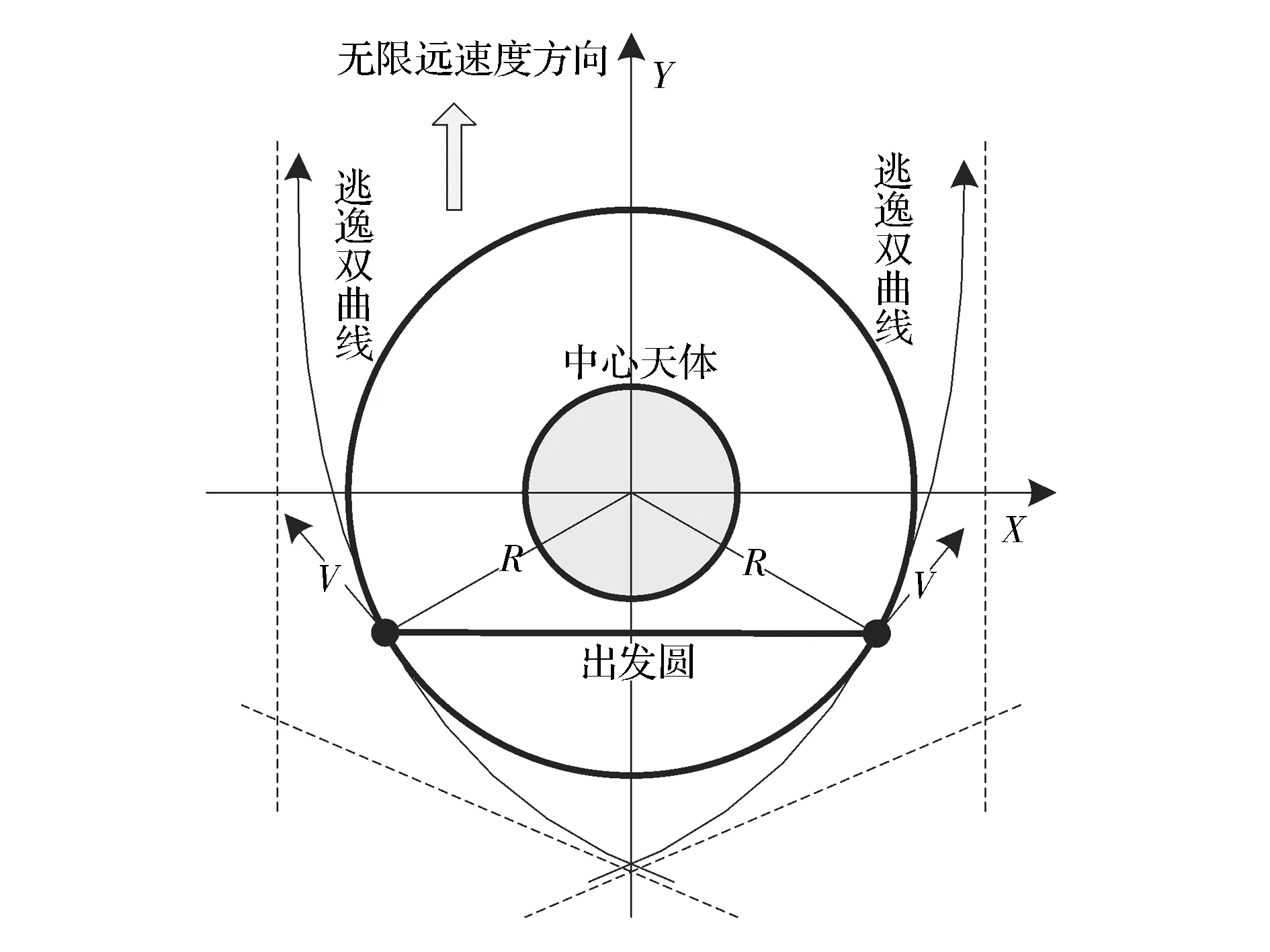
图2 二体模型逃逸出发圆概念图Fig.2 Concept figure of LEDC of two-body model

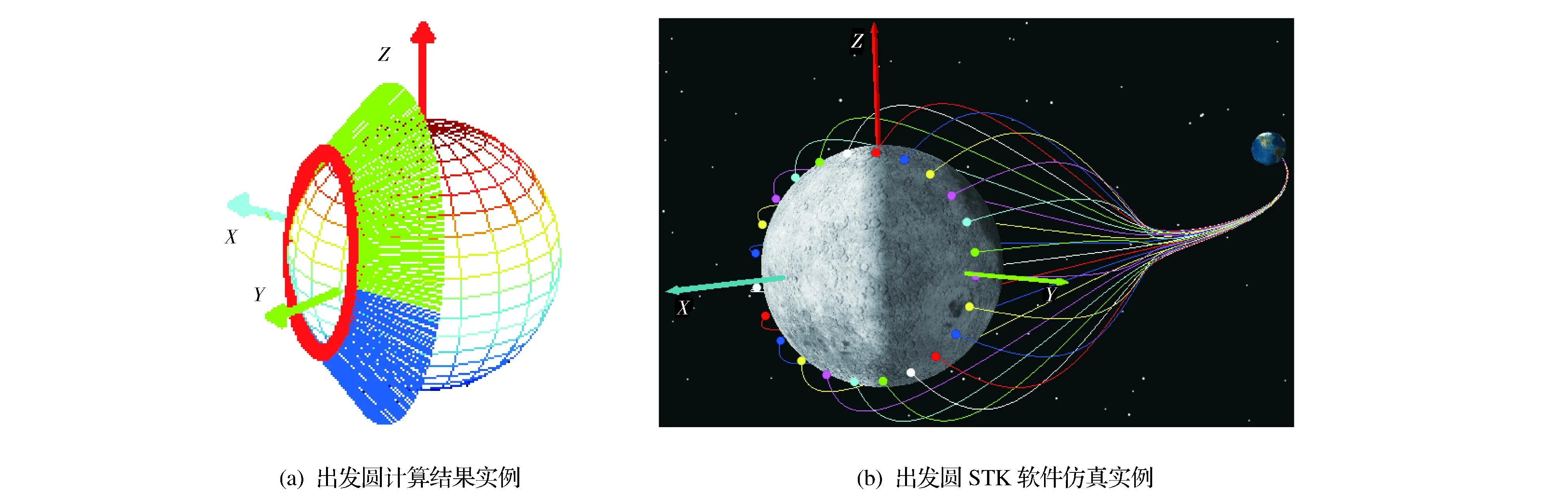
图3 月地转移出发圆图例Fig.3 An example figure of LEDC

由出发圆定义可知，出发圆参数的影响因素包括：转移时长和无限远速度方向。在月地转移问题中，影响因素转换为出发时刻、再入时刻、地球相对月球的位置和再入点约束。

月地转移出发圆问题的分析图如图4所示。逃逸月球后速度方向大致指向再入时刻地球位置，地球位置由θn=w(t0-tn)表示，其中w为月球公转角速度，t0为出发时刻，反映初始地月位置关系，tn为再入时刻，反映终时地月位置关系，由于N为(t0-tn)四舍五入取整的结果，因而t0和N也可以描述地球的位置。由于白道瞬时坐标系与地心的相对位置关系较为稳定，因而出发时刻月球位置关系影响较小。由于再入速度和再入点纬度具有相对稳定性[8]，再入点高度和再入角严格约束，再入点经纬度在定点着陆约束下取值区间较小，因而可大范围变化的再入约束只有返回轨道倾角。

综上，月地转移出发圆主要影响因素为转移时间和返回轨道倾角。基于以上结论，文章分析参数N和iE对出发圆参数的影响。

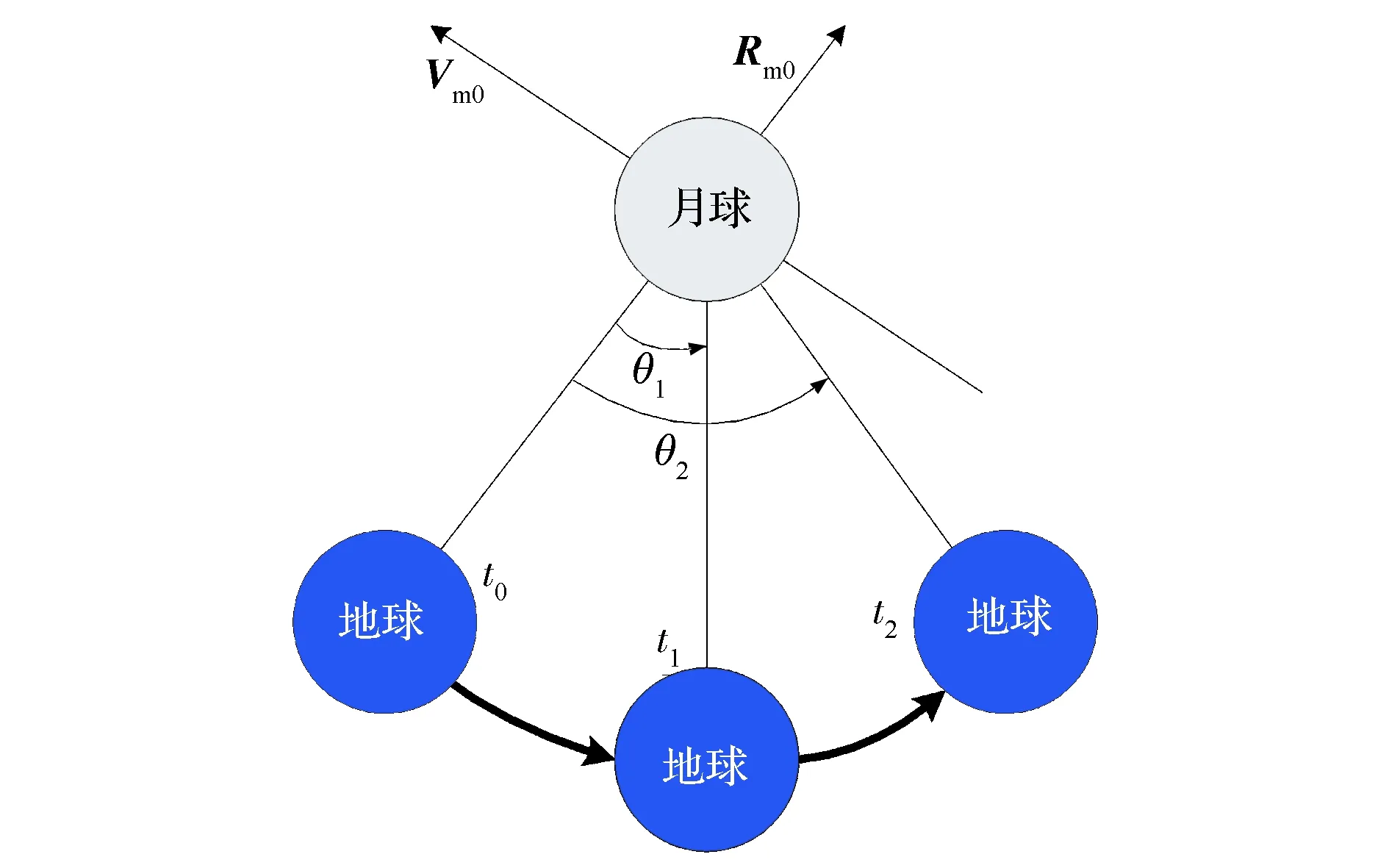
图4 月地转移出发圆分析图Fig.4 Analytical figure of LEDC

3.2 转移时间参数N对出发圆的影响

采用前文所述模型，截取图3中三维出发圆的XY平面视图，分析同一时刻出发的情况下，N为变量时的出发圆参数。N的取值为N={2,3,4,5}，以某着陆场为目标着陆场，环月轨道高度取120km， 返回轨道倾角取55°，计算结果如图5所示。由图5可知，出发圆转动情况与3.1节分析相吻合。

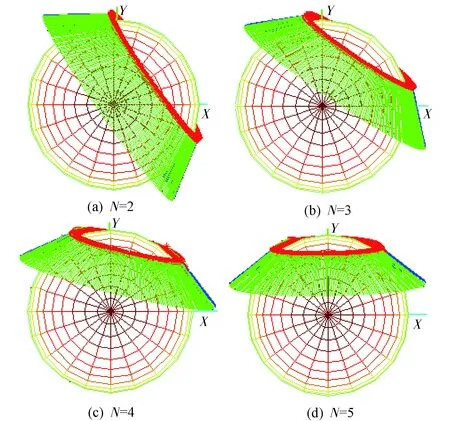
图5 出发圆位置随N值的变化Fig.5 Position of LEDC varies with N

分析出发速度变化图(图6)可知：①转移时间相同，出发点越靠近月球速度方向出发速度越小，N=5时的最小出发速度约2 440.13 m/s；②升轨出发速度略小于降轨出发速度，两者之差最大约2 m/s，最小约0.2 m/s；③返回时间参数N对出发速度的影响远远大于出发点位置等的影响，出发位置相同，N=2和5时的出发速度相差最大约280 m/s，N=2时，不同出发点的出发速度相差约7.5 m/s，N=5时，不同出发点的出发速度相差只有约0.33 m/s。

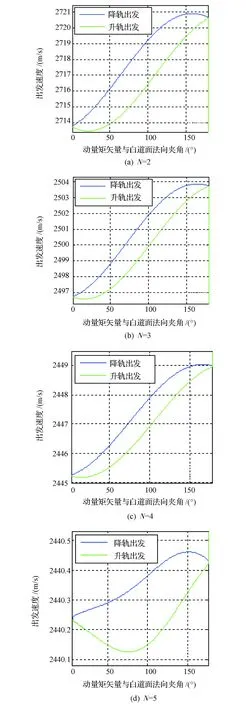
图6 出发圆速度随N值的变化Fig.6 Velocity varies with N

3.3 返回轨道倾角iE对出发圆的影响

基于3.2节分析结果，采用前文模型，以N和iE为变量，其中N={2,3,4,5}，iE=[55° 65° … 125°](返回轨道倾角大于55°可保证飞行器降落在北半球，故设其为下限，而返回轨道倾角大于125°时，再入速度过大，故设其为上限)，出发圆的星下点和速度需求分布如图7～图10所示。

分析可得结论：①一系列返回轨道倾角对应的出发圆星下点形成一簇闭合的条带，显示出发圆在月球瞬时轨道坐标系中的转动；②返回轨道倾角增大，出发速度随之增大，变化范围较大，N=2时，该范围达到约220 m/s，N=5时，也有约90 m/s的变化范围；③N是出发圆位置的主要影响因素，当N值给定后，出发圆具有一定稳定性，轴线转动最大约20°。

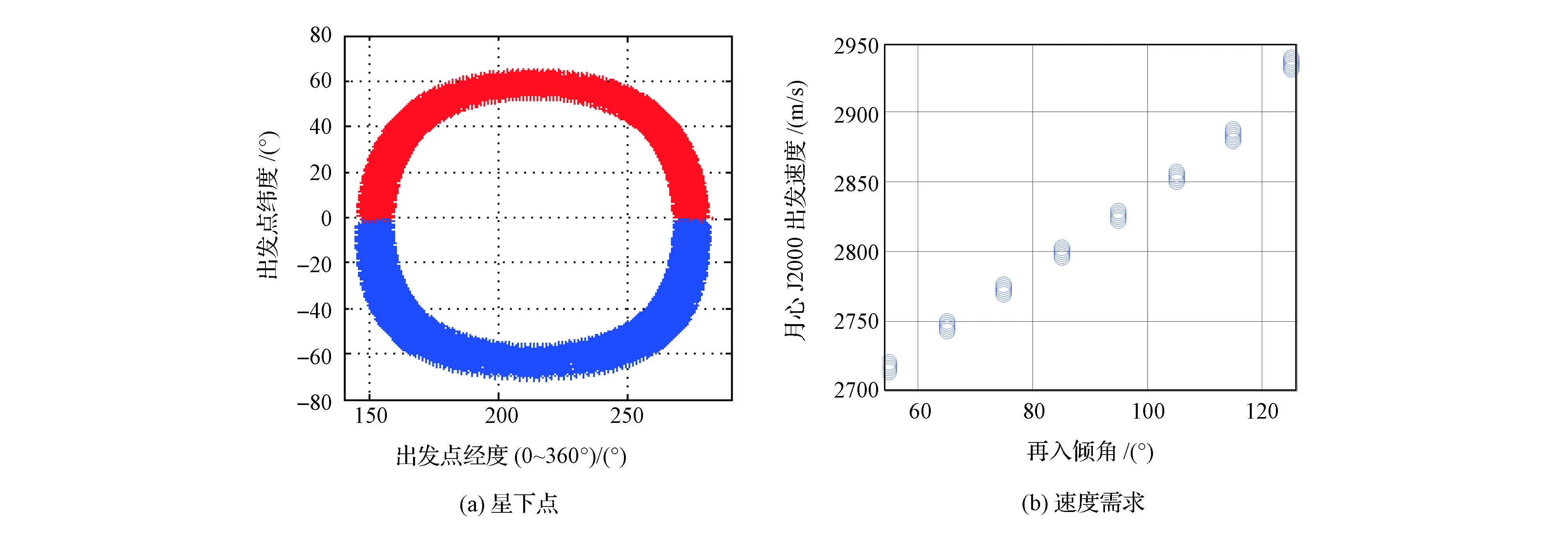
图7 N=2的出发圆参数Fig.7 Parameter of LEDC as N=2

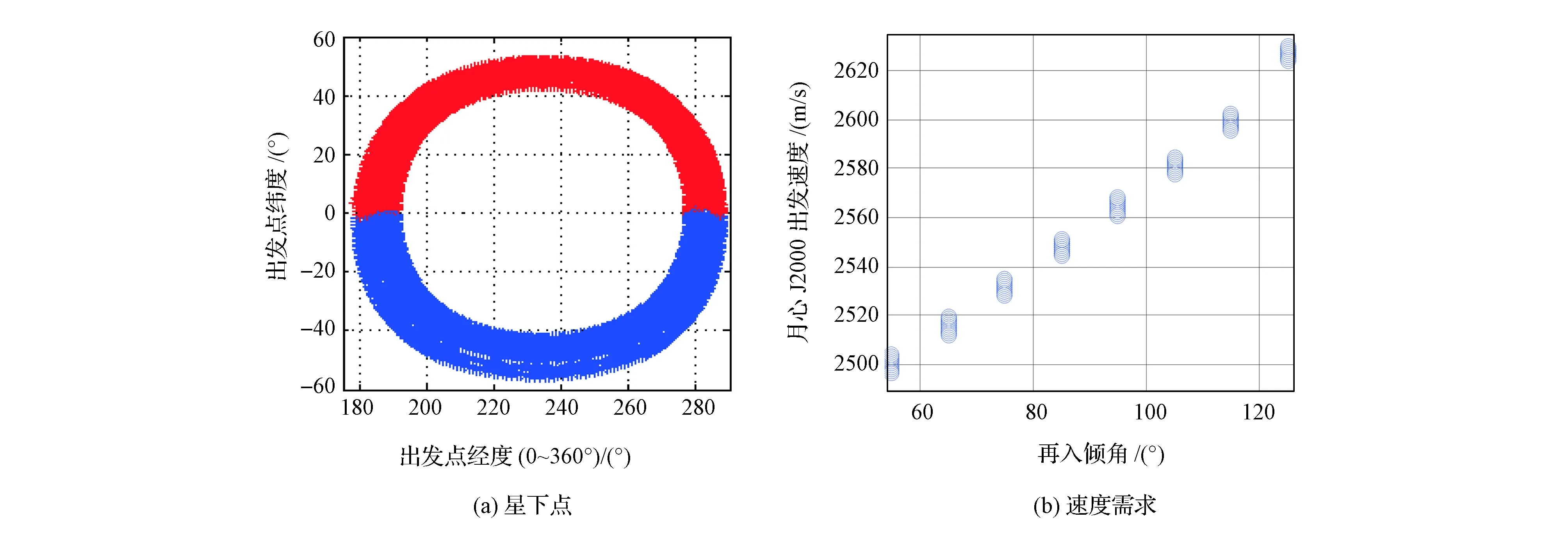
图8 N=3的出发圆参数Fig.8 Parameter of LEDC as N=3

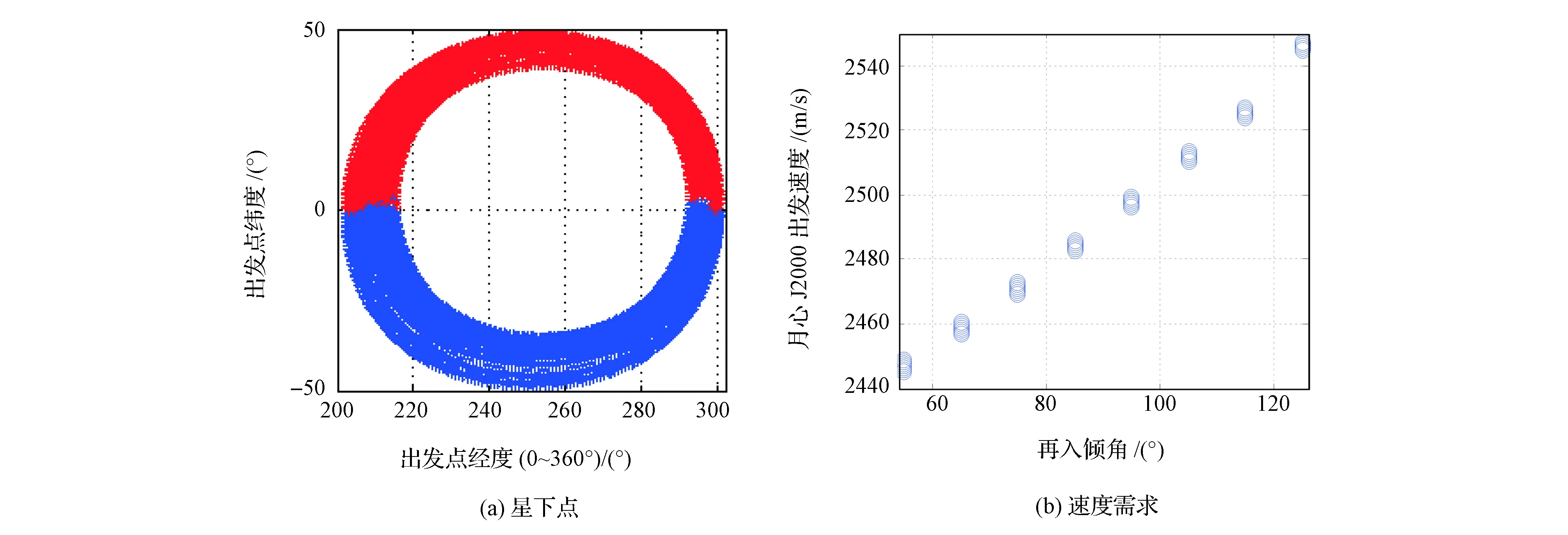
图9 N=4的出发圆参数Fig.9 Parameter of LEDC as N=4

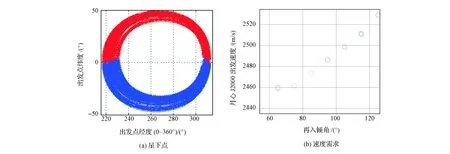
图10 N=5的出发圆参数Fig.10 Parameter of LEDC as N=5

4 环月段返回能力分析

1)基于出发圆制定返回机动策略

出发圆代表了该出发时刻及约束对应的出发点可选位置，由出发圆定义可知，出发圆圆心与月心不重合，因而环月轨道未必与出发圆有交点，即使有交点，轨道面与返回出发轨道面也可能夹角不为零，此即不可直接返回的环月轨道，需要执行变平面机动。

针对有交点但不垂直的情况，机动流程为：①选择出发速度方向与当前轨道交点处速度方向在出发圆平面同一侧的交点为出发点；②建立以该交点为近月点，以交点和月心连线为拱线的大椭圆过渡轨道；③在第一次到达过渡轨道远月点时实施变平面机动，改变量为交点处返回轨道面与过渡轨道面的夹角；④到达近月点时，实施加速即可返回地面指定着陆场。

针对无交点情况，机动策略计算流程为：①出发圆与球心构成圆锥， 确定轨道面与该圆锥所有母线中夹角最小的母线，确定该母线对应的返回轨道参数；②确定返回轨道面内轨道高度与当前环月圆轨道高度相同的圆轨道参数，确定该轨道与当前圆轨道交线；③以该交线为拱线，实施近月点加速，构造当前轨道面内大椭圆过渡轨道；④远地点实施变平面机动，使轨道面与返回轨道面重合；⑤择机实施Lambert机动，目标点为返回出发点；⑥到达出发点后加速，返回地面。一个返回机动算例(图11)如表1、表2所示。

图11 环月返回机动算例Fig.11 An example of return from lunar orbit

无交点情况是最为恶劣的环月段返回情况，变平面速度增量需求超过300 m/s，同时消耗大量时间，应该尽量避免环月轨道进入与出发圆无交点的情况。

表1 原轨道参数

2)环月段返回能力定义

由前文建模和分析知，出发圆主要影响因素为N和返回轨道倾角，其中返回轨道倾角对系统方案影响有限，能够代表系统返回能力的参数与N相关。当N给定后，在定点着陆约束下，返回时间在(N-0.5，N+0.5)d内变化，速度增量需求受其影响变化较大，对应的最大速度增量能够保证环月段返回最长时间不超过N+0.5 d。另一方面，返回时间参数N能对飞船环控生保系统等非再生分系统支持能力提出明确要求。

表2 返回机动参数

因而环月段返回能力采用与返回时间密切相关的参数来表示能够兼顾速度增量需求和非再生系统资源需求，适宜作为环月返回能力系统指标，定义返回能力Nr：返回能力Nr指飞行器具备从环月轨道到达再入点的转移时间不大于(Nr+0.5) d的能力，Nr为整数。Nr值越小，返回机动能力越强，对应的其它系统支持能力必须大于等于(Nr+0.5) d。

统计前文计算分析结果，某时刻环月轨道高度为120 km情况下，不计变平面需求，不同的返回能力Nr对应的速度增量需求如表3所示。

表3 环月段返回速度增量需求

5 结论

本文梳理了月地转移轨道快速设计模型，提出了出发圆的概念，识别了出发圆参数主要影响因素为转移时间和返回轨道倾角，并分析了出发圆参数变化规律。给定N值后，出发圆具有一定稳定性，基于此分析了环月段返回机动策略。最终确定了Nr作为环月段探测器返回能力的定义。在探测器具备从环月段2.5 d内返回地面的能力要求下，速度增量需求约1320 m/s；当探测器能提供的月地转移速度增量为“星座”计划中标称返回情况对应的约900 m/s时[9]，只能保证5.5 d内从环月段返回地面。

References)

[1]N R Campbell, M G Hinton, E Perchonok. Space rescue operations volume III: appendices,ATR71(7212-05)-1[R]. El Segundo,Aerospace Corporation,1971:51-56

[2]贺波勇,李海阳,张波.载人登月转移轨道偏差传播机理分析与稳健性设计[J].物理学报 ,2013(19)

He Boyong, Li Haiyang, Zhang Bo.Analysis of transfer orbit deviation propagation mechanism and robust design for manned lunar landing[J]. Journal of physics, 2013(19)

[3]Huang Wende, Xi Xiaoning, Wang Wei. Characteristic analysis and design of near moon abort trajectory for manned lunar landing mission[J].Science China Technological Sciences, 2010,53(11):3129-3137

[4]彭坤, 徐世杰. 一种无奇异的求解Lambert变轨的普适变量法[J].北京航空航天大学学报,2010,36(4):399-402

Peng Kun, Xu Shijie. Singularity free universal variables method to solve Lambert transfer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010,36(4) :399-402 (in Chinese)

[5]Luo Q, Meng Z, Han C.Solution algorithm to a Quasi-Lambert’s problem with fixed flight-direction angle constraint[J]. Celestial Mechanics and Dynamical Astronomy, 2011, 109(4):409-427

[6]李立涛,张振民,杨涤.奔月转移轨道的快速设计方法研究[J].航空学报,2003,24(2):152-156

Li Litao, Zhang Zhenming, Yang Di.Study of rapid design method for cislunar transfer trajectory[J]. Acta Aeronautica et Astronautica Sinica, 2003,24(2):152-156

[7]Wilson S W. A pseudostate theory for the approximation of three-body trajectories[C]// AAS AIAA Astrodynamics Conference. Santa Barbara, California: AAS Publication Office, 1970:84-96

[8]沈红新,李海阳,彭祺擘,等.探月飞行器定点返回轨迹特性分析[J].国防科技大学学报,2011,33(4):6-11

Shen Hongxin, LIi Haiyang, Peng Qibo. Point return trajectory characteristics analysis for a lunar spacecraft[J]. Journal of National University of Defense Technology, 2011,33(4):6-11

[9]果琳丽，王平,彭刊. 载人月球基地工程[M]. 北京：中国宇航出版社, 2013:656-657

Guo Linli, Wang Ping, Peng Kun. Manned lunar base project[M]. Beijing: China Astronautics Press, 2013:656-657

(编辑：张小琳)

Analysis of lnfluence Factors on Return Velocity from Lunar Orbit

RAO Jianbing1XIANG Kaiheng1PENG Kun2

(1 Beijing Institute of Electronic System Engineering, Beijing 100854, China) (2 Beijing Institute of Manned Space System Engineering, Beijing 100094, China)

A lunar orbiter may be required to return to the earth. Because of high nonlinearity of the orbit dynamics model, it is difficult to analyze the return mechanism. In order to solve the problem, a lunar-earth transfer orbit design model is built and a concept of lunar-earth departure circle (LEDC) is developed. The main influence factors on the parameters of LEDC are confirmed to be transfer timeNand return inclination, and then the varying law of the parameter caused by the influence factors is analyzed. As the return time parameterNis given, the LEDC is stable. And the return policy is studied based on the conclusion. Finally,Nris defined as the parameter to describe the system’s capability of returning to earth and the velocity increments needed for variousNrare given.

lunar orbit; return orbit; lunar-earth departure circle

2014-04-25；

2015-07-13

饶建兵，男，硕士，研究方向为航天器轨道与总体设计。Email：raojianbing2007@163.com。

V412.41

A

10.3969/j.issn.1673-8748.2015.04.004