基于最小二乘法和递推最小二乘法的雷达伺服跟踪系统建模
2015-03-12合肥工业大学安徽合肥230009中国电子科技集团公司第38研究所安徽合肥230088
李 红(1.合肥工业大学,安徽合肥 230009;2.中国电子科技集团公司第38研究所,安徽合肥 230088)
基于最小二乘法和递推最小二乘法的雷达伺服跟踪系统建模
李红1,2
(1.合肥工业大学,安徽合肥230009;2.中国电子科技集团公司第38研究所,安徽合肥230088)
摘要:雷达伺服转台的精确建模是实现高性能控制的基础,传统的机理建模准确性有待提高。设计并实现了雷达伺服转台的系统辨识实验,对所得现场数据应用最小二乘(Least Squares)和递推最小二乘算法(Recursive Least Squares algorithms),获得雷达伺服转台的传递函数模型。
关键词:雷达;伺服系统;系统建模;最小二乘算法
0 绪论
雷达伺服系统作为雷达的重要组成部分,是一种精密伺服系统,其技术水平的高低直接影响到跟踪精度乃至整个雷达的性能。对系统的模型结构和参数有确定的认知是实现对被控对象的精确控制的基础。目前对雷达伺服系统进行建模,多采用机理建模,此方法的优点是思路清晰、理论成熟[1-3]。但由于转动惯量、摩擦、齿轮间隙等结构因素的影响[4],机理建模所得模型与实际系统有较大出入;另外投入使用后设备会在各方面发生很大变化,理论数据的可靠性将值得质疑。文[5]以机理建模的方法得到雷达伺服系统稳定平台直流力矩电机驱动器的结构框图;文[6]列写电压方程、运动方程、转矩方程,可得到各个轴的传递函数。本文在机理建模的基础上,对雷达三轴稳定平台进行系统辨识建模,建立离散脉冲传递函数描述系统的输入输出关系。
1 辨识算法的基本原理
1.1最小二乘法
最小二乘类参数辨识方法包括最小二乘及其他改进算法,其中最小二乘法最基本,应用广泛。本文以雷达伺服转台的方位角度控制系统为研究对象,对该单输入单输出(Single Input Sin⁃gle Output,SISO)系统进行建模和参数辨识研究,如图1所示。

图1 SISO过程的辨识
记录可测的输入u(k)和输出y(k)数据序列;用过程模型,即脉冲传递函数G(z-1)用来描述过程的输入输出特性,通常,其中A(z-1)和B(z-1)分别为阶数na,nb的多项式。不确定因素的影响归结为附加噪声e(k),则
A(z-1)y(k)=B(z-1)u(k)+e(k),变成最小二乘格式y(k)=h'(k)θ+e(k),其中:
h(k)=[-y(k-1),…,-y(k-na),u(k-1),…,u(k-nb)]'
θ=[a1,a2,…,ana,b1,b2,…,bnb]'
对于k=1,2,3,…,L,方程构成线性方程组,写作yL=HLθ+eL
yL=[y(1),y(2),…,y(L)]',eL=[e(1),e(2),…,e(L)]'。
对于ARX模型,取准则函数J(θ):
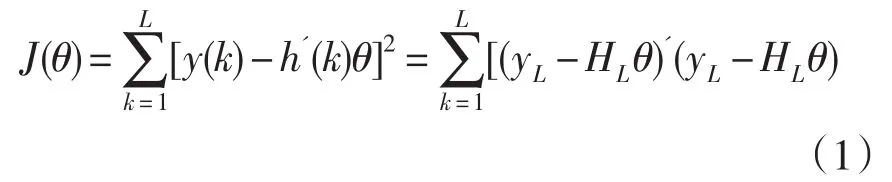
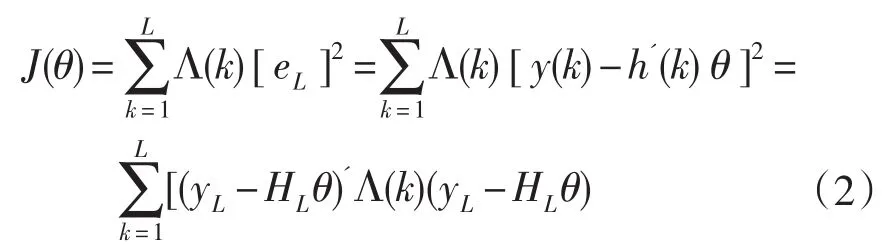
1.2递推最小二乘法
最小二乘法递推算法RLS(recursive least squares)的基本思想可以概括成[9]:当前估计值̂(k ) =上一步估计值̂(k+1 ) +当前修正值。
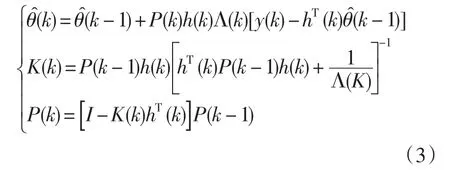
计算过程中可能出现舍入误差,为了保证p(k)的对称性,有时把上组式子中的第三式写为:
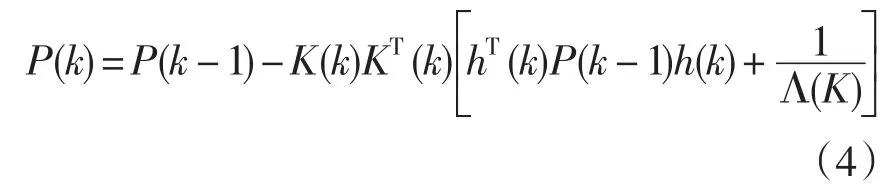
递推计算需要事先选定初始参数θ̂(0)和P(0),可根据一批数据利用一次性完成算法预先求得,也可直接取:
P(0)=α2I,α为充分大的实数,̂(0)=ε,ε为充分小的实向量。(5)
2 辨识试验的设计
2.1先验知识的获取
作为常见的军用产品,雷达伺服系统的非线性一般在设计的过程中即被严格控制,并采用电流负反馈环路、高精度线性检测元件等手段克服其非线性的影响。所以本系统的非线性程度降到了最低程度。同上原因,可认为本系统是SISO的线性时不变系统。表1写出了原有系统的各重要性能指标。
2.2输入信号的选择
为了满足参数辨识和建模的要求,输入信号必定存在一定的约束条件。首先,在辨识时间内雷达伺服系统的过程动态必须被输入信号持续激励,或者说,在实验期间输入信号必须充分激励过程的所有模态[9]。其次,为了避免进入非线性区,输入信号的幅度或功率幅度不宜过大;但也不能太小,以免数据所含的信息量下降,直接影响辨识的精度。实验初期采用的是幅值为3°的阶跃,但在应用最小二乘法(1)式进行辨识时,出现病态矩阵无法求逆,可用最小二乘的递推算法进行求解。本实验选择了伪随机信号M序列(线性移位寄存器序列)作为辨识输入信号。将4级移位寄存器输出的逻辑0和逻辑1变换成3°和-3°的阶跃序列,如图2所示。
2.3采样时间和辨识时间的选取
对连续时间进程进行辨识时,输入输出信号需经过采样处理。采样时间的选择直接影响辨识模型的结构与精度,除需满足采样定理外,必须统筹考虑控制器精度、计算和存储能力、辨识算法计算时间、执行机构响应速度等因素。本文系统辨识试验中选取的采样时间为0.01秒。

表1 原系统的阶跃响应技术指标
辨识时间的选取即数据长度的选定。现有系统的调整时间为0.5秒,即阶跃响应0.5秒后,系统基本处于稳定状态。考虑到留有余地、数据录取系统的方便性及适应具体辨识算法,辨识时间初步选定为12秒,其中前2秒为阶跃前零过程,后10秒为阶跃响应过程。
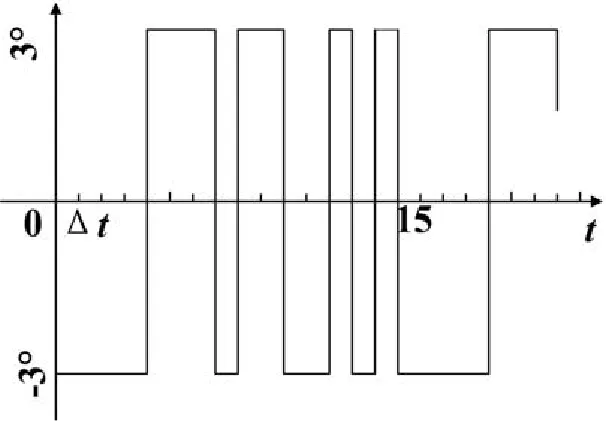
图2 4级M序列变换成幅值为3°和-3°的序列
3 雷达伺服跟踪系统结构介绍[5]
机载SAR稳定平台直流力矩电机驱动器由位置环、稳定环、速度环和电流环的四闭环系统共同组成。雷达伺服系统中,速度环路是一个重要的内环路,它不仅能够提高系统的低速平稳性,扩大系统的调速范围,且能够增强系统抵抗负载扰动的能力。
4 辨识结果
雷达伺服转台的传递函数模型结构如下:

4.1最小二乘法辨识结果
输入为M序列一次完成最小二乘的辨识结果:a1=-4.031 0,a2=6.621 0,a3=-5.631 0,a4=2.523 0,a5=-0.481 4,b1=0.010 5,b2=0.013 8,b3=-0.050 4,b4=0.018 9,b4=0.007 2。
4.2递推最小二乘法辨识结果
最小二乘一次完成算法占用大量内存,不适合在线辨识。为减少计算量及所占数据存储量,应用递推最小二乘参数的辨识过程如图3所示。初始值直接按式(5)选定,最终输出结果:a1=-4.016 3,a2=6.573 7,a3=-5.572 3,a4=2.488 6,a5=-0.473 6,b1=0.010 5,b2=0.013 9,b3=-0.050 0,b4=0.018 4,b4=0.007 1。

图3 递推最小二乘参数的辨识
5 结论
本文设计并实现了雷达伺服转台的系统辨识实验,对输入输出现场数据应用最小二乘算法和递推最小二乘算法进行处理,在机理分析的基础上对雷达伺服系统进行参数辨识建模,获得其五阶线性脉冲传递函数模型。该模型可真实的反应雷达伺服系统的输入输出关系,为精确的控制器设计奠定基础,为提高雷达跟踪性能创造了理论条件。
参考文献:
[1]潘高峰,周江.船载雷达伺服系统的建模与仿真[J].电子工程师,2007,33(6):7-9.
[2]李兰,房建成,韩潮.基于SIMULINK的惯性平台稳定系统的建模与仿真[J].中国惯性技术学报,2005,13(2):19-23.
[3]薛辉,李萍.基于MCU+EPLD的雷达天线转台通用伺服系统设计[[J].机电工程技术,2013(7):60-62.
[4]李正大,陈光达,马洪波.结构因素对雷达伺服系统性能影响及其测试研究[J].现代电子技术,2008,266(3):33-36.
[5]王振收.机载SAR稳定平台直流力矩电机驱动器[J].现代雷达,2006,28(3):70-75.
[6]熊峰.机载雷达伺服系统研究与仿真[J].电讯技术,2003(2):1-4.
[7]·I lyas Eker,Open-loop and closed-loop experimental on-line identification of a three-mass electromechanical system,Mechatronics[J]. 2004(14):549-565.
[8]Ivan Markovsky,Sabine Van Huffel,Overviewoftotal least-squares methods[J]. Sig⁃nal Processing,2007(87):2283-2302.
[9]侯媛彬,汪梅,王立琦.系统辨识及其MATLAB仿真[M].北京:科学出版社,2004.
(编辑:阮毅)
The Identification and Simulation of Radar Servo-System Based on the Least Squares Method and Recursive Least Squares
LI Hong1,2
(1. Hefei University of Technology,Hefei230009,China;2. The 38th Research Institute of CETC,Hefei230088,China)
Abstract:The precise modeling of the radar servo system is the basis of high performance controller. The precision of traditional mechanism model needs to be improved. Based on the system identification theory,the Least Squares and Recursive Least Squares algorithms are used to obtain transfer function model of the radar servo system.
Key words:radar;servo system;system identification;least squares algorithm
作者简介:李红,男,1980年生,硕士研究生,高级工程师。研究领域:天线伺服系统、稳定平台和机载环境控制系统。已发表论文4篇。
收稿日期:2015-05-12
DOI:10. 3969 / j. issn. 1009-9492. 2015. 11. 006
中图分类号:TN953
文献标识码:A
文章编号:1009-9492 ( 2015 ) 11-0023-03
猜你喜欢
杂志排行
机电工程技术的其它文章
- TinyOS环境下交通信息采集自组网系统设计**国家自然科学基金资助项目(编号:50878088);广东省高等学校学科建设专项项目(编号:2013WYXM0133);广东省高等学校优秀青年教师培养计划资助项目(编号:Yq2013180)。
- 舵机加载系统及其伺服驱动器控制参数设置方法**航空科学基金资助项目(编号:20130863006)
- 基于海马号ROV富钴结壳的钻取技术研究**国家高技术研究发展计划(863计划)资助项目(编号:GZH201100307-04-01)
- 大摆锤驱动头动力学建模与仿真研究**国家质检总局科技计划项目(编号:2014QK255)
- 基于ArtCAM的十二生肖浮雕加工研究**江苏省大学生实践创新计划项目(编号:201412808005Y)
- 一种多工位全自动玩具喷涂机的设计
