一种基于LSH的时间子序列匹配查询算法
2015-03-12刘根平陈叶芳杜呈透钱江波
刘根平,陈叶芳,杜呈透,钱江波
(宁波大学信息科学与工程学院 宁波 315211)
1 引言
时间序列是按时间顺序排列、随时间变化且相互关联的数据序列[1,2]。时间序列数据出现在各种各样的领域中,包括科学计量、财务数据、传感网络、音频、视频和人类活动等。在这些序列中,典型查询有找出股票价格趋势相似的公司、找到与某公司有相似销售模式的公司、找到近几个月和某产品销售模式相似的例子等。
时间序列的相似性查询可分为全序列匹配查询和子序列匹配查询。全序列匹配查询是从时间序列数据集中找出所有与查询序列在整体上相似的时间序列,即给定N个数据序列 S1,S2,…,SN、一个查询序列 Q以及相似性阈值ε,找到所有与Q相似性小于ε的数据序列。这里,数据序列和查询序列长度相等。例如,给定一支股票,已知它在2012-2014年每日的收盘价,要找出这3年中与它相似的所有股票,这个问题就是全序列匹配问题。子序列匹配查询则是从比查询序列长很多的时间序列中找出所有与查询序列相似的子序列的位置偏移和长度,即给定N个不同长度的数据序列S1,S2,…,SN、一个查询序列Q以及相似性阈值ε,找到所有与Q相似性小于ε的子序列。如给定一支股票,已知它在2003-2005年每日的收盘价,在过去30年中找出与该股票3年走势相似的股票。
子序列匹配是全序列匹配的一般化问题。在数据库序列远长于查询序列,且最优子序列匹配可能出现在数据库的任何位置时,实现高效的子序列匹配是一个重要的问题[3]。对于现实世界中的应用,如哼唱查询(query by humming,QbH)、手写文档中的字识别以及大型视频数据库和动作捕捉数据库中基于内容的检索等,改进子序列匹配算法意义重大。
子序列匹配的算法已有很多,Faloutsos等人[4]提出FRM算法,把数据库序列划分成滑动窗口,查询序列划分成翻转窗口,窗口大小为u,最后把这些窗口用离散傅立叶变换(discrete fourier transform,DFT)转换成 f维的点,它能处理不同长度的子序列查询。与查询序列相似的子序列能在数据库的任意位置找到。然而,通过把数据序列划分成滑动窗口,FRM产生太多的点需要存储。DualMatch方法[5]解决了FRM算法的这一问题。它把数据库序列划分成翻转窗口,查询序列划分成滑动窗口。数据库序列划分成翻转窗口后,DualMatch方法把需要存储的点降低到FRM算法的 1/u。
虽然通过DFT后,时间序列的主要特征被提取出来,但不能保证提取的特征是完整的,且转换后点的维度f的值不能太大,否则建立的索引结构会遭遇维数灾难。为避免这一问题,本文不通过DFT的方法对时间序列进行处理,而是采用局部敏感散列(locality sensitive hashing,LSH)技术。
LSH有坚实的理论依据,在高维数据空间中表现优异。LSH的基本思想是将距离近的对象以很高的概率散列到同一个桶中,而距离远的对象以很低的概率散列到同一个桶中。通过这样的处理,可以过滤很多不相似的对象,避免不必要的比较,从而大大提高检索速度。因此,被广泛应用于许多场景中,包括基于内容的图像检索[6]、音频检索[7]、视频复制检测[8,9]等。
2 相关工作
2.1 序列匹配
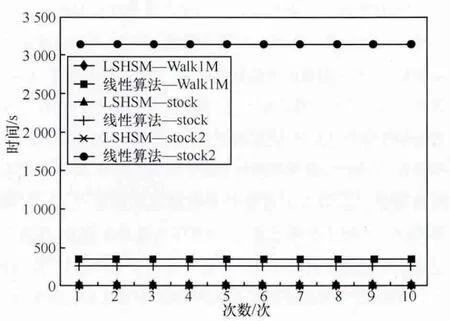
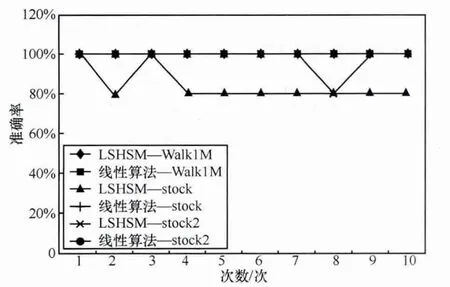
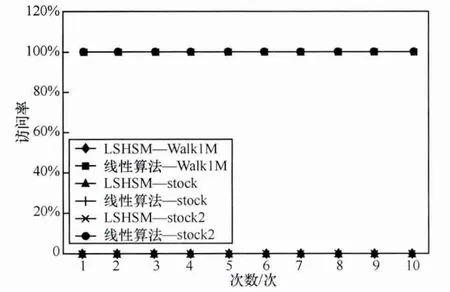
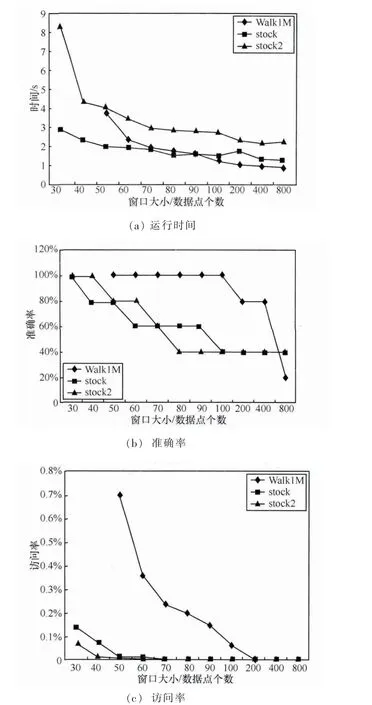
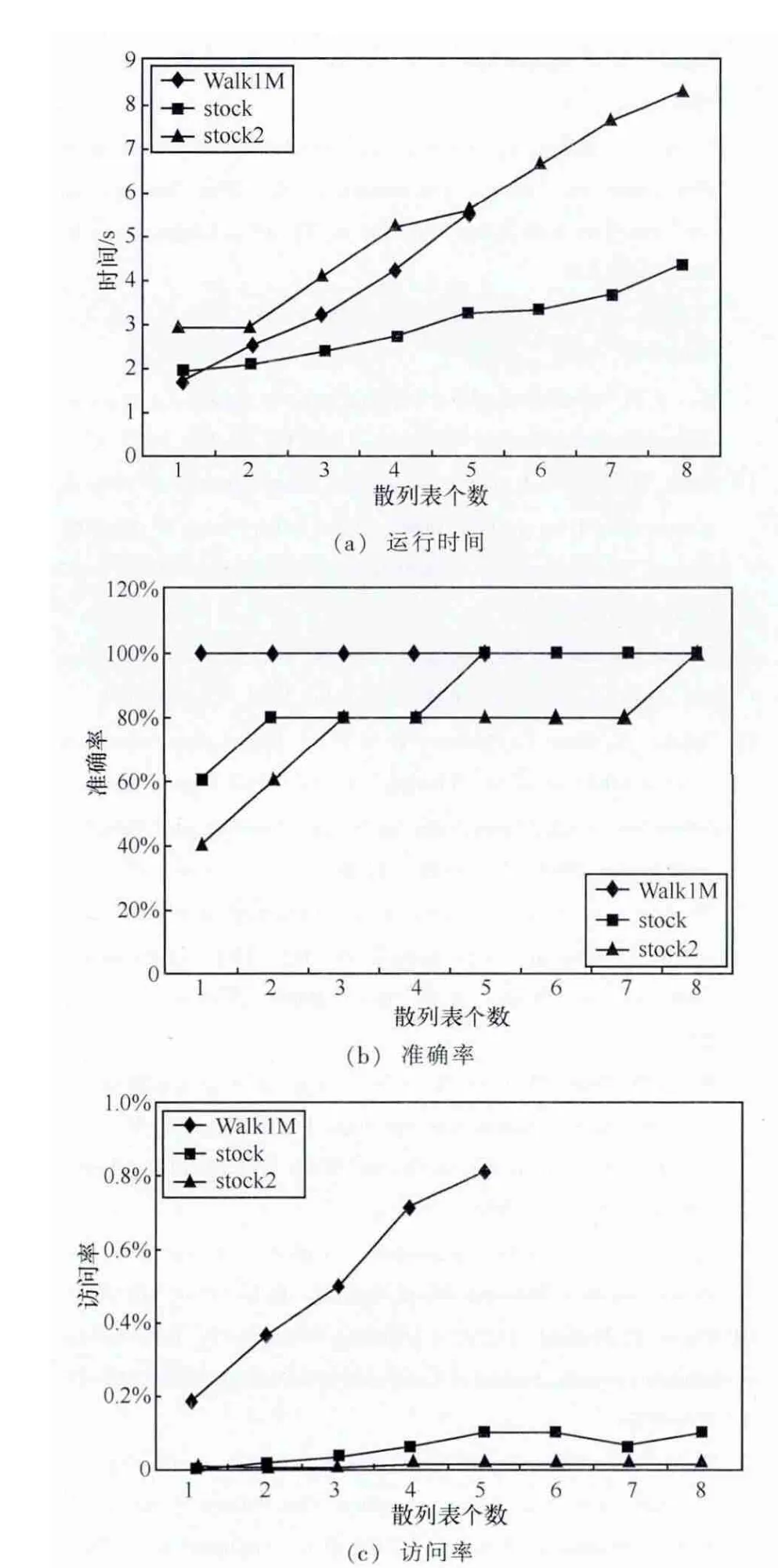
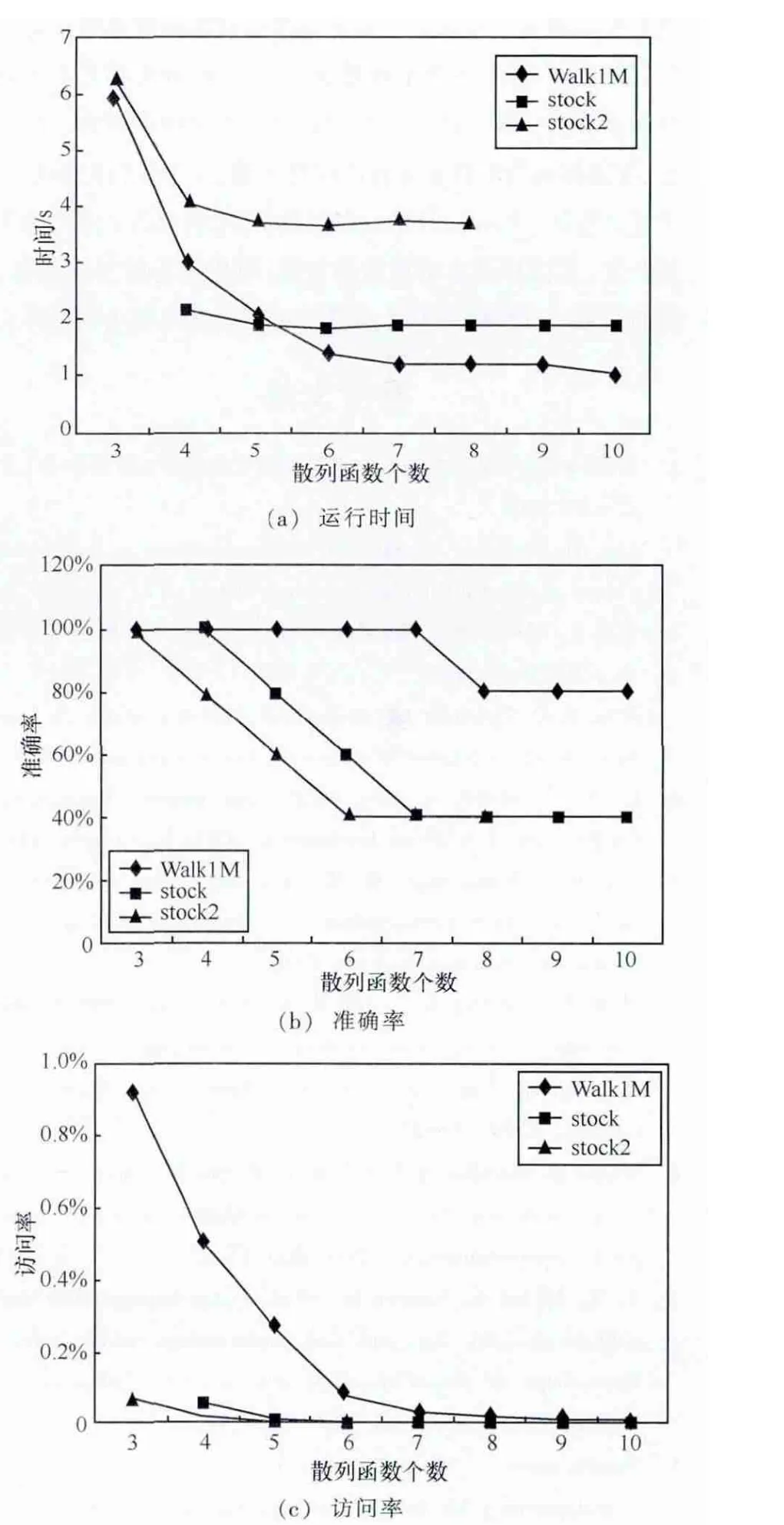
全序列匹配第一次出现在Agrawal[10]的文章中,它的主要思想如下:首先,把长度为n的数据库序列通过DFT转换到频域空间,分别提取它们的前f个特征(f FRM算法是Faloutsos[4]提出的,用来解决子序列匹配问题。它包括索引建立和子序列匹配两个阶段。在索引建立阶段,首先把数据库序列划分成大小为u的滑动窗口,对每个窗口进行DFT,转换为f维的点;然后把这些点组织成最小边界矩形 (minimum bounding rectangle,MBR);最后把MBR存储在R*-tree中。在子序列匹配阶段,当查询序列Q到来时,把它划分成大小为u的翻转窗口。对每个窗口进行DFT,转换为f维的点,然后每个点在R*-tree中进行范围查询,找到候选集,最后进行验证,得到相似子序列。 由于FRM算法把数据库序列划分成滑动窗口,存储这些数据需要很大的空间消耗,DualMatch[5]解决了这一问题。DualMatch在构造窗口时与FRM算法相反,它把数据库序列划分为翻转窗口,查询序列划分为滑动窗口。通过把数据库序列划分为翻转窗口而不是滑动窗口,使R*-tree需要的数据存储空间减小到原来的1/u,减少了所需的存储空间,但它允许的窗口大小比FRM算法小。DualMatch可以直接在索引中存储数据点,而不是最小边界矩形。 以上方法不管如何划分时间序列,在划分完之后,都要通过特征提取函数对窗口进行特征提取,形成f维的点,这个过程实质是一个降维的过程。但提取的特征不能保证信息的完整性,且f的值不能太大。因为f太大,索引的性能会受到影响,导致维度灾难。基于这个考虑,本文采用LSH算法对时间序列进行处理。 局部敏感散列算法[11,12]是一种适合高维数据的流行算法。它的主要思想是距离相近的点会以很高的概率散列到同一个桶中,距离远的点散列到同一个桶中的概率会很低。它的定义如下[13]。 定义1 散列函数族H={h:S→U}是(r1,r2,p1,p2)-敏感的,如果对于任意的v,q∈S有 (其中S为d维点的数据空间,D:S×S→R 为相似性度量): ·如果 D(v,q)≤r1,则 PrH[h(v)=h(q)]≥p1; ·如果 D(v,q)≥r2,则 PrH[h(v)=h(q)]≤p2。 为使 LSH 的散列函数族有效,需要保证 r1<r2,p1>p2。 不同的距离度量有不同的LSH函数。欧式距离下的LSH 函 数 为[14]: 其中,x是d维的向量,a是另一个d维向量,它的每一维都服从p-稳定分布。当p=2时,这个分布为均值为0、方差为1的高斯分布N(0,1)。a·x是向量a和x的点积。w是一个常量,变量b服从[0,w]的均匀分布。 通过使用LSH,可以保证距离近的点冲突的概率大于距离远的点。这样可以过滤很多不相似的对象,避免不必要的比较,从而大大提高检索速度。因此,被广泛应用于许多场景中,包括基于内容的图像检索、音频检索、视频复制检测等。 [6]使用LSH进行卫星图像检索,参考文献[15]使用LSH对局部描述子进行索引,参考文献[16]中使用LSH进行3D物体索引,参考文献[7]中使用两级LSH索引机制对多变音轨进行检测,许多视频复制检测系统也使用LSH创建索引[8,9]。除此外,LSH还被用于处理Web数据。参考文献[17]使用LSH对Web数据进行重复检测。Google news使用min-hash对Web上的新闻进行协同过滤[18]。在生物数据方面,Buhler[19,20]使用LSH对大规模的DNA序列进行相似性比对。参考文献[21,22]利用LSH进行离群点的检测,参考文献[23]中利用LSH对时间序列产生散列签名,并把对象不冲突的概率作为距离,然后利用这个距离进行剪枝操作。 与参考文献[23]不同,本文把数据库序列划分为大小相等的翻转窗口,查询序列划分成滑动窗口。但不采用DFT对窗口进行转换,而是把划分好的每个窗口看成一个高维的点,直接用LSH对窗口进行散列,既保留了时间序列信息,又会避免维度灾难。通过散列步骤把数据库序列的窗口建成索引;待查询序列到来时,用查询序列的窗口在索引中进行查询,得到候选序列。 本文所用的符号及含义见表1。 表1 符号及含义 定义2 时间序列S是一个随时间变化的有序序列S=<(t1,s1),(t2,s2),…,(tm,sm),>。其中(ti,si)(i∈[1,m])表示 ti时刻的值为si,后文为方便把S简记为S=s1,s2,…,sm。 时间序列可以很长,有时包含上亿个观察值。但在本文中,只关注时间序列的子部分,即时间子序列。 定义3 时间序列S的子序列Si,j是起始于si,终止于sj的短序列,Si,j=si,si+1,…,sj。 定义5 序列 X=x1,…,xN,Y=y1,…,yN是 ε-匹配,当且仅当 D(X,Y)≤ε。 引理1[4]如果长度相同的两个序列Si和Qii是ε-匹配,则任意的序列对(Sij,Qij)也是ε-匹配。即: 这个引理保证了用窗口进行处理时不会有假阴性的序列。 引理2[5]当长度相同的两个序列S和Q分别划分为p个窗口wsi和 wqi(1≤i≤p),如果 S和 Q是 ε-匹配,则至少有一对对应的窗口(wq,ws)是-匹配。即: 要解决的问题是:给定一个查询序列,在给定的数据库中找出与查询序列最相似的几个子序列。 首先把数据库序列分成大小为u的翻转窗口,不采用DFT,而直接把这个窗口看成u维的点,利用LSH的散列函数h对这些窗口进行散列。 LSH算法是一个“过滤+验证”的框架。从LSH的原理可以看出,散列函数的过滤效果越好,需要进行的距离计算次数会越少,查询效率也会越高。即距离近的窗口冲突的概率越大,距离远的窗口冲突的概率越小,LSH的查询质量和查询效率就会越高。如果只使用一个LSH函数会产生很多的假阳性点,过滤效果不理想。但如果使用的散列函数个数太多,又会导致假阴性点增多。所以从H散列函数族中随机均匀独立地选择k个hi(·)组成函数g(·)= 待给定的查询序列Q到来后,先把它划分成长度为u的滑动窗口wqi,每次滑动一格。对每个窗口分别计算g1(wqi)、g2(wqi)、…、gL(wqi)。以落入散列表 Tj(·)的桶 gj(wqi)中的所有窗口作为候选集。 经过上述处理,假设与查询窗口wq距离为r的窗口通过h(·)散列与wq冲突的概率为 p0,那么该窗口与 wq在L张散列表中至少冲突一次的概率为1-,于是与wq距离不大于r的点被作为查询结果而返回的概率就不小于1-。选择合适的k、L会得到比较好的结果。 这样对于候选集中的所有窗口,计算其起始偏移位置,获取与查询序列Q长度相同的子序列作为候选子序列,比较其与Q之间的距离,选出距离最近的K个子序列。 所以对数据序列的每个窗口根据式 (1)进行散列计算,计算k次,得到一个g(·),存储在散列表中,如此重复L次,得到L个散列表,这样就建立好了索引。待查询序列Q到来时,首先把它划分成滑动窗口,总共有|Q|-u+1个滑动窗口,对每个窗口同样运用LSH进行散列处理,取出Q的每个窗口所在的L个桶g(·)中的数据序列窗口,由之前分析可知,这些窗口将以1-(1-pk0)L的概率被返回。 图1说明了LSH处理序列的过程。数据序列S被划分成翻转窗口,ws是它的一个窗口。每个窗口经过两个g(·)函数处理后,映射到散列表T1、T2中。查询序列Q到来时,首先划分成滑动窗口,wq是它的一个窗口。wq经过两个g(·)处理后,映射在T1的2号桶中、T2的2号桶中。取出这两个桶中的数据序列窗口作为候选,进行后处理。在后处理中,由于要找的与查询序列长度相同的子序列,所以要计算子序列的起始偏移。图2描述了计算子序列起始偏移的过程。 图1 LSH处理过程 图2 算法后处理 3.3.1 构建索引算法实现 输入:数据库序列S,窗口大小u,LSH参数k、L。 输出:LSH索引。 构建索引算法的实现步骤如下: (1)初始化索引; (3)对于每个窗口,对L个散列表中的每个表,用LSH散列函数hi进行散列值的计算,重复k次; (4)存储信息到散列表中。 3.3.2 查询算法实现 输入:索引,查询序列Q。 输出:与Q相似的子序列。 查询算法实现步骤如下。 (1)初始化。把Q划分为|Q|-u+1个滑动窗口。 (2)查询索引。对于每个滑动窗口,对L个散列表中的每个表,用LSH散列函数hi进行散列值的计算,重复k次,得到桶信息;取出窗口所在桶的所有数据当成候选。 (3)后处理。对候选集中的每个记录;在数据库中找出对应的子序列;计算与Q的距离;若相似,则输出。 本节将通过合成数据集和真实数据集来评估本文所提出算法的性能,并和线性扫描算法进行比较。算法用Java语言实现,实验在Intel Core i3-3203.3 GHz、4 GB内存的机器上进行。 利用几个常用的用于评估算法的时间序列数据集,包括合成数据集Walk1M、真实数据集stock和stock2,它们的数据集信息见表2。 表2 数据集信息 (1)Walk1M Walk1M[4,5,25]包含1000000个数据点。它的第一个点设置为1.5,而其之后的点是通过在前一个点的基础上加上一个范围在[-0.001,0.001]的随机值形成的。 (2)stock stock数据集包含纽约证券交易所的408家公司25年中每日的收盘价。数据集是从Yahoo Finance[26]收集的。序列总长度为1916833个数据点。 (3)stock2 stock2[26]数据集包含纽约证券交易所的 500家公司25年中每日的开盘价。数据集是从Yahoo Finance收集的。每个序列长度为6480个数据点,把所有序列级联成一个长序列,长度为3240000个数据点。 LSHSM算法是一个近似算法,需要验证它的有效性。因此,采用与线性扫描算法进行Top5查询对比的方式验证LSHSM算法的有效性。 (1)评价标准 3个评价标准:运行时间、准确率、访问率。 运行时间:在相同运行环境下,算法运行时间越少,说明算法越有效。 假设查询点为Q,用I(Q)表示查询返回的结果集合,A(Q)表示数据集中所有满足查询条件的点的集合。召回率和精度的定义为: 召回率recall表示查询结果集中满足查询条件的点的数量与数据集中所有满足查询条件点的数量比例,精度precision表示查询结果集中满足查询条件的点的数量与查询结果集中所有点的数量的比例[27]。在Topk查询中,召回率等于精度。用召回率表示准确率。 访问率是指访问数据库的比例。用C(Q)表示LSH查询得到的候选子序列集合,M(Q)表示数据库中所有长度为|Q|的子序列集合。访问率可以表示为: (2)算法的有效性 图3、图4、图5验证了LSHSM算法的有效性。在实验中,由于各数据集的特性各不相同,所以LSHSM算法取的参数值不尽相同。在Walk1M数据集中,窗口大小u为100,散列表个数L为1,散列函数个数k为5;stock数据集中,窗口大小u为50,散列表个数L为2,散列函数个数k为4;stock2数据集中,窗口大小u为50,散列表个数L为3,散列函数个数k为3。 图3 与线性扫描算法运行时间的对比 图4 与线性扫描算法准确率的对比 图5 与线性扫描算法访问率的对比 图3、图4、图5分别是LSHSM算法与线性扫描算法在3个数据集中进行Top5查询运行10次的运行时间、准确率、访问量的对比。可以看出,LSHSM算法的运行时间有很大的提高;LSHSM算法的准确率接近100%,几乎和线性扫描相同;相比于线性扫描,LSHSM算法访问的数据库比率小了3个数量级。 实验证明LSHSM算法是有效的,且性能比线性扫描算法有极大的提高。 LSHSM算法中参数k、L、u的选择对算法性能有很大的影响。k太小,散列到同一个桶的概率比较大,得到的候选对象会很多,其中包括许多假阳性对象,增加计算开销;k太大,散列到同一个桶的概率变小,得到的候选对象变少,这样不仅把假阳性对象过滤掉,同时也把真正近似的对象过滤掉,准确率不高。L越小,散列到同一个桶中的概率越小,得到的候选对象越少,找到真正近似对象的准确性越低;L越大,散列到同一个桶中的概率越大,得到的候选对象越多,找到真正近似对象的准确性越高,但同时访问数据库的比率会越大。所以,需要考虑这两个参数的影响,使算法的性能最好。 实验中考虑3个参数对算法性能的影响:散列表的个数L、散列函数个数k以及划分窗口大小u。理论上来说,u越大,LSHSM算法计算越快,u太大可能导致找不到相似子序列。另一方面,u越小,越能精确找到子序列,准确度越高,但是窗口太小,LSHSM算法所花的时间会越多。 在 Walk1M 数据集中,k=5,L=1,u=80;stock 数据集中,k=4,L=2,u=50;stock2 数据集中,k=4,L=3,u=50。实验中,在改变其中一个参数时,其他两个参数固定不变。 (1)窗口大小u对算法的影响 图6显示了在固定k和L时,窗口大小u对算法性能的影响。 图6 窗口大小u对算法性能的影响 从图6中可以看出,u变大时,算法构建的索引会减小,查询窗口个数也随着减小,时间呈整体下降的趋势。但随着u的增大,LSH得到的候选集会减小,导致假阴性节点增加,算法的准确性会有所下降。 (2)散列表个数L对算法的影响 图7显示了在固定k和u时,散列表个数L对算法性能的影响。L达到一定数值,准确率已达到很高,再继续增大L,得到的效果也已经达到饱和。特别是Walk1M数据集中,在L=5时的效果已经非常好,没有必要再进行更大L的比较。 从图7中可以得出,其他参数固定时,随着散列表个数的增加,算法构建的索引增大,需要查询的散列表增多,候选集增加,因此数据访问率呈增长趋势,查询所用的时间也呈上升趋势。散列表个数增大会增加两个对象冲突的概率,使得算法准确性增加。 (3)散列函数个数k对算法的影响 图8显示了在固定u和L时,散列函数个数k对算法性能的影响。 图7 散列表个数L对算法性能的影响 图8 散列函数个数k对算法性能的影响 从图8可知,其他参数固定时,随着散列函数个数k的增加,候选集会减少,数据访问率会降低,所需查询时间呈下降趋势。但是随着散列函数个数的增加,会把真正的近邻散列到其他桶中,准确率会有所下降。 时间序列的相似性查询已有很长的研究历史,在子序列匹配问题中,传统基于树的方法虽然能很好地解决低维空间的问题,但当数据维度增加时,它们的效果甚至不如线性扫描算法。本文提出了用LSH技术与时间序列结合的方法,既能避免高维数据导致的维度灾难,又能保留时间序列的主要特征。利用LSH的局部敏感性,把相似的子序列聚集到一起,过滤掉很多不相似的对象,减少所需的比较次数,提高效率。实验结果表明,该方法在性能上有很大的提升。 参考文献 1 肖辉.时间序列的相似性查询与异常检测(博士学位论文).复旦大学,2005 Xiao H.Similarity search and outlier detection in time series(doctor dissertation).Fudan University,2005 2 曾海泉.时间序列挖掘与相似性查找技术研究 (博士学位论文).复旦大学,2003 Zeng H Q.Research on mining and similarity search in time series database(doctor dissertation).Fudan University,2003 3 Fu T.A review on time series data mining.Engineering Applications of Artificial Intelligence,2011,24(1):164~181 4 Christos F,Ranganathan M,Manolopoulos Y.Fast subsequence matching in time-series databases.Proceedings of ACM SIGMOD Conference,Minneapolis,USA,1994 5 Moon Y S,Whang K Y,Loh W K.Duality-based subsequence matching in time-series databases.Proceedings of the 17th International Conference on Data Engineering,Heidelberg,Germany,2001:263~272 6 Ruben B,Homaifar A,Gebril M,et al.Satellite image retrieval using low memory locality sensitive hashing in Euclidean space.Earth Science Informatics,2011,4(1):17~28 7 Yi Y,Michel C,Vincent O,et al.Local summarization and multi-level LSH for retrieving multi-variantaudio tracks.Proceeding soft he17th ACM International Conference on Multimedia,Beijing,China,2009:341~350 8 Paisitkriangkrai S,Mei T,Zhang J,et al.Scalable clip-based near-duplicate video detection with ordinal measure.Proceedings of the ACM International Conference on Image and Video Retrieval,Xi’an,China,2010:121~128 9 Zhu L,Liu T,Gibbon D,et al.Effective and scalable video copy detection.Proceedings of the 11th ACM International Conference on Multimedia Information Retrieval,Philadelphia,USA,2010:119~128 10 Agrawal R,Faloutsos C,Swami A.Efficient similarity search in sequence databases.Proceedings of the 4th International Conference FODO,Chicago,USA,1993:69~84 11 Indyk P,Motwani R.Approximate nearest neighbors:towards removing the curse of dimensionality.Proceedings of the 30th Annual ACM Symposium on Theory of Computing,Dallas,USA,1998:604~613 12 Gionis A,Indyk P,Motwani R.Similarity search in high dimensions via hashing.Proceedings of the 25th International Conference on Very Large Data Bases (VLDB),Edinburgh,UK,1999:518~529 13 甘骏豪.基于动态碰撞检测的位置敏感哈希(硕士学位论文).中山大学,2013 Gan J H.Locality-sensitive hashing scheme based on dynamic collision counting(master dissertation).Sun Yat-sen University,2013 14 Datar M,Nicole I,Indyk P,et al.Locality-sensitive hashing scheme based on p-stable distributions.Proceedings of the 20th Annual Symposium on Computational Geometry,New York,USA,2004:253~262 15 Yan K,Sukthankar R,Huston L.Efficient near-duplicate detection and sub-image retrieval.ACM Multimedia,2004,4(1):869~876 16 Bogdan M,Shan Y,Sawhney H S,et al.Rapid object indexing using locality sensitive hashing and joint 3D-signature space estimation.IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(7):1111~1126 17 Manku G S,Jain A,Sarma A D.Detecting near-duplicates for web crawling.Proceedings ofthe 16th International Conference on World Wide Web,Banff,Alberta,Canada,2007:141~150 18 Das A S,Datar M,Garg A,et al.Google news personalization:scalable online collaborative filtering.Proceedings of the 16th International Conference on World Wide Web,Banff,Alberta,Canada,2007:271~280 19 Buhler J. Efficient large-scale sequence comparison by locality-sensitive hashing.Bioinformatics,2001,17(5):419~428 20 Buhler J.Provably sensitive indexing strategies for biosequence similarity search.Journal of Computational Biology,2003,10(3~4):399~417 21 Wang Y,Parthasarathy S,Tatikonda S.Locality sensitive outlier detection:a ranking driven approach.Proceedings of the IEEE 27th International Conference on Data Engineering(ICDE),Hannover,Germany,2011:410~421 22 Pillutla M R,Raval N,Bansal P,et al.LSH based outlier detection and its application in distributed setting.Proceedings ofthe 20th ACM International Conference on Information and Knowledge Management,Glasgow,Scotland,UK,2011:2289~2292 23 汤春蕾,董家麒.基于LSH的时间子序列查询算法.计算机学报,2012,35(11):2228~2236 Tang C L,Dong J Q.Similarity query oftime series subsequences based on LSH.Chinese Journal of Computers,2012,35(11):2228~2236 24 李俊奎.时间序列相似性问题研究 (博士学位论文).华中科技大学,2008 Li J K.Research on time series sequence similarity(doctor dissertation).Huazhong University of Science and Technology,2008 25 MoonY S,WhangK Y,HanW S.Generalmatch:a subsequence matching method in time-series databases based on generalized windows.Proceedings of the ACM SIGMOD International Conference on Management of Data,Madison,Wisconsin,USA,2002:382~393 26 CaiY,Ng R.Indexing spatio-temporaltrajectories with Chebyshevpolynomials.Proceeding soft he ACM SIGMOD International Conference on Management of Data,Baltimore,Maryland,USA,2004:599~610 27 凌康.基于位置敏感哈希的相似性搜索技术研究 (硕士学位论文).南京大学,2012 Ling K.Research on locality sensitive hashing-based similarity Search(marster dissertation).Nanjing University,20122.2 局部敏感散列
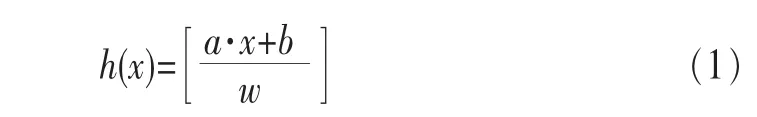
3 LSHSM算法及实现
3.1 基础知识

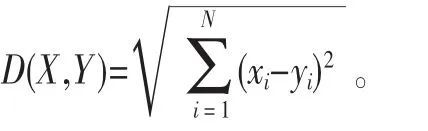
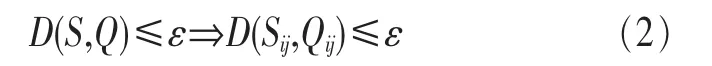
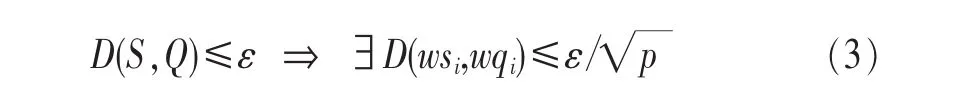
3.2 LSHSM算法的思想
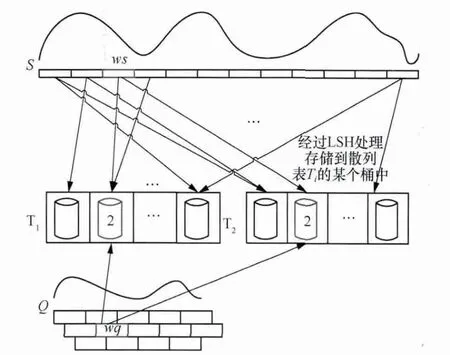
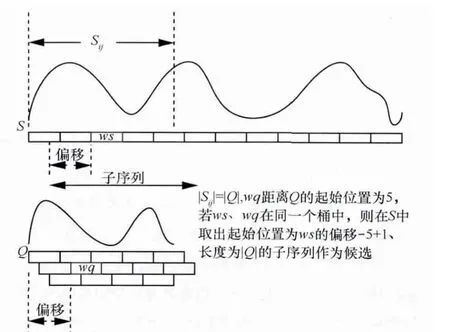
3.3 算法实现
4 实验验证
4.1 数据集
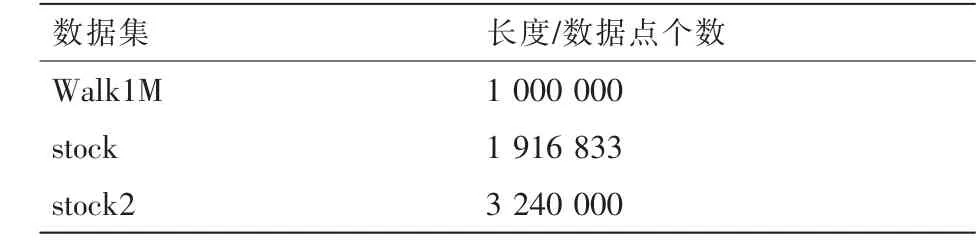
4.2 实验对比
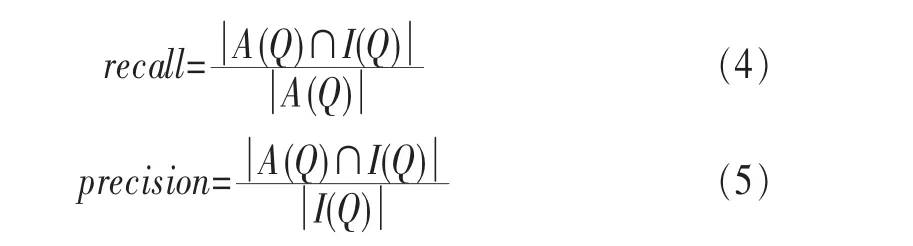
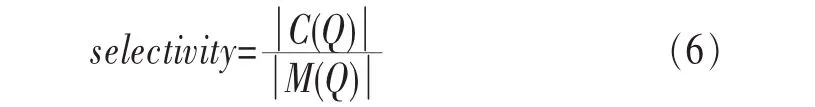
4.3 参数的影响
5 结束语
