紧急疏散状态下人群疏散时间的不确定性分析

刘 宇，高 瞩，2，张望梧

(1．西安理工大学，陕西 西安 710054;2．常州工学院，江苏 常州 213002;3．南通中能机械制造有限公司，江苏 南通 226575)

0 引言

随着经济和文化的迅猛发展，公共建筑成为人们经济和文化的主要空间，各种娱乐、大型商业、宣传等公共活动的主要集散地，具有密度高、流量大及环境特殊等特点。公共建筑中一旦发生紧急事件，将会造成重大经济损失和人员伤亡。因此，公共建筑的安全问题已引起国家和人们的高度重视，业界正在强化对其的研究力度。

人群疏散的不确定性对于人群疏散时间最小化有重要的影响，对其的研究在国内外已有很长的历史，早期疏散研究一直沿用观察为主的数据获取方法，故难以获得疏散数据，更无法得到人群疏散的种种不确定性因素。如Togawa、Melinek和Booth以及Pauls通过观察和经验总结出不同场景下的疏散时间计算公式［1－3］。由于疏散过程中存在许多不确定性因素的影响，简单的经验计算公式无法反映出人群疏散时间的不确定性。计算机仿真模拟技术的发展，已使许多计算机模型可以仿真出模拟人员的疏散时间［4－5］，但是计算机模型仅局限于反映疏散环境对于人群疏散时间的影响。为此，本文利用多项式混沌展开法，对人员密度、人群组成、单个人员预动时间等不确定性因素展开分析，研究出人群疏散的各种影响。

1 紧急疏散过程的描述

图1 疏散过程

人员疏散过程是一个非常复杂的过程，涉及当事人的心理、生理及疏散环境等各方面的因素［6］。疏散过程一般分为反应过程和疏散运动过程两部分，如图1所示。的确定存在较大难度，如人群密度、人群组成和预动时间等。由于这些参数的可变性和随机性，可将这些参数视为不确定性参数。确定性因素是指公共建筑内部出口的相关参数。

通过对疏散过程的分析，可知疏散时间与确定性参数和不确定性参数相关。人群的疏散时间表示为

式中:x={x1，x2，…，xna，xan+1，…，xna+nb}是参数的集合，其中包括确定性参数和不确定性参数;x1，x2，…，xna为确定性参数集合，na为确定性参数的个数;xna+1，…，xna+nb为不确定性参数集合;nb为不确定性参数的个数;na+nb为参数的输入个数。

2 多项式混沌展开法

反应过程是指紧急事件发生到开始疏散的过程。反应过程主要是指当事人对紧急事件的识别和响应，此过程可分为识别过程和响应过程。识别过程是指发生紧急事件到当事人确认的过程。在识别过程中，当事人的运动不受警告信号的影响，但识别过程受疏散环境、人员特性、建筑物运营管理的影响［7］。响应过程是指确认紧急事件发生到开始疏散的过程。在响应过程中，当事人会有预动作。疏散运动过程是从开始疏散到疏散结束的过程。疏散运动过程受到疏散环境和当事人运动特性的影响，如路线的选择、当事人运动速度以及人与人之间的相互作用等。在疏散运动过程中，当事人的运动速度由其人员特性决定，且在疏散运动过程中不断地发生变化，人员的疏散行为及决策的选定也存在不确定性。

人群的疏散过程是一个极其复杂的过程，且含有许多不确定的因素。人群疏散过程与个体人员特性(如人员性别、年龄、运动能力和人群密度等)、人员对紧急事件的识别、路线的选择、人员心理与生理等因素相关［8］。根据参数的可控性，可将人群疏散时间的影响参数分为确定性参数和不确定性参数。由于紧急事件的发生和人群的个体行为存在随机性，使人群疏散中某些相关参数

多项式混沌展开是由齐次混沌理论演变而来［9］，主要用于有限二阶矩计算过程的随意性描述［10］。基于人群疏散时间的不确定性，可通过多项式混沌展开方法来处理。

结合多项式混沌展开使用条件，可构建疏散时间数学模型T:

①假设确定性参数x1，x2，…，xna在设定范围内服从均匀分布。

②输入参数 x1，x2，…，xna，且相互独立。

不确定参数作用下的疏散时间可表示为

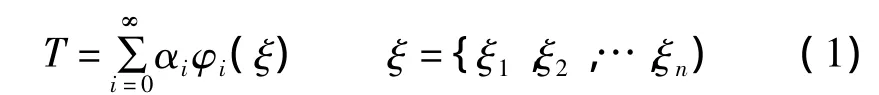
式中:αi(i=0，1，2，…，n)为多项式混沌展开系数;ξ={ξ1，ξ2，…，ξn)为随机变量;φi(ξ)是以随机变量ξ为参量的多维正交多项式。

为便于计算，可将输入参数 x={x1，x2，…，xn}根据下式转化为均值为0、方差为1的随机变量 ξ={ξ1，ξ2，…，ξn)。

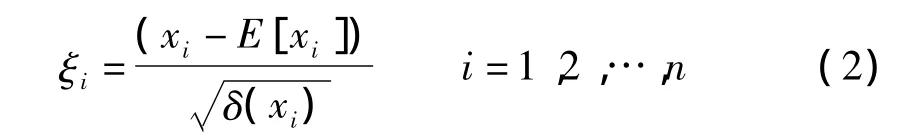
式中:E(xi)为xi的期望;δ(xi)为xi的方差。由式(2)可知，若已知 ξi，可求得 xi。

为方便估计输出量的不确定性［11］，式(1)中T的多项式混沌展开截断到其中的某一阶数。如下式所表达的T关于随机变量ξ的a阶截断多项式混沌展开。

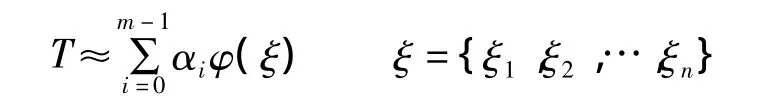
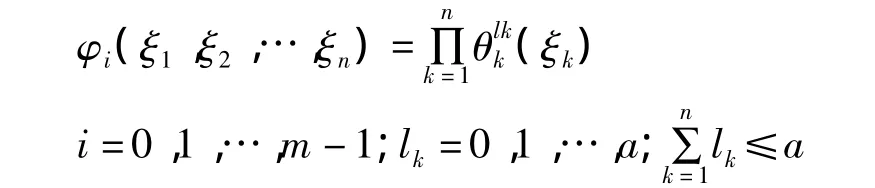
式中，θlkk(ξk)是以随机变量ξk为参量的lk阶一维正交多项式。

3 人群疏散时间的不确定性分析

3.1 疏散模型的构建

3.1.1 人群疏散量的定义与描述

疏散过程是一个连续性过程，且每个人的位置和速度都是连续变化的，所以连续性模型更能准确反映人群疏散的过程。关于连续性模型的研究，Helbing提出的社会力模型能够较好地反映人与人、人与紧急事件、人与建筑物之间的相互作用［12］。基于社会力模型的研究，运用芬兰VTT研究中心开发的FDS+Evac计算机疏散模型中提出的运动方程来控制，人员控制方程为

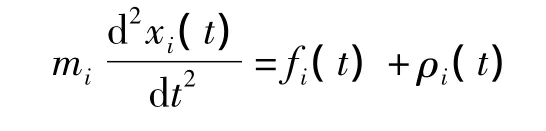
式中:xi(t)为人员i在t时刻的位置;fi(t)为周围环境对人员i在t时刻施加的作用力;mi为人员i的重量;ρi(t)为人员i在t时刻受到人员之间的作用力;人员i的速度可表示为vi(t)=d xi/d t。

3.1.2 人群疏散时间的计算模型构建

由于人群疏散的不确定性是固定存在，且不能将其排除在外，关于人群疏散时间不确定性的处理方法，本文运用Anylogic软件对每个疏散场景进行多次模拟，来获得平均人员疏散时间作为该场景下的疏散时间。

运用Anylogic疏散模型对疏散场景进行重复模拟的方法如下:

①保证平均人员疏散时间的收敛性，确定最小模拟次数nmin;

②运用Anylogic软件进行nmin次重复模拟获得平均疏散时间;

上述步骤中平均疏散时间T的收敛性可通过相对误差l来判断，即

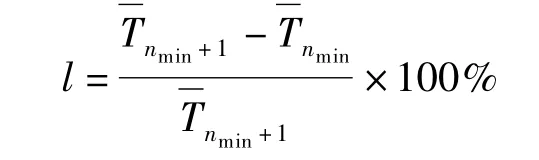
一旦获得疏散时间，便可获得在不确定参数影响下人群疏散时间的期望E(T)、方差δ(T)，分别分析出人群密度、人群组成和人员预动时间对疏散时间的影响。

3.2 示例

3.2.1 案例描述

以地铁站台为例，假设地铁站台层的建筑面积为200 m2，将上行自动扶梯和楼梯看为出口。由于地铁展开两侧均有上行楼梯和自动扶梯，所以出口数分为2个(A和B出口)，且2个出口均在中间位置，出口宽度设定为3.5 m，人员密度均值约为1.0人/m2，如图2所示。

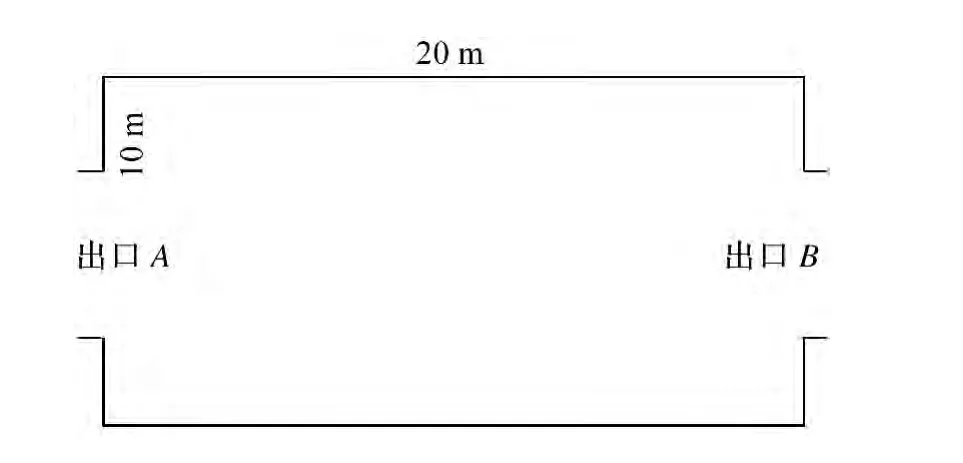
图2 地铁站台简图

此处考虑的不确定性因素包括人群密度、人员组成和预动时间，这些参数根据文献［13］的研究课题获取，如表1～3所示。为方便计算，本文假定人群密度在整个空间内是均匀的，故预动时间服从正态分布［14］。

表1 人群密度调研 人·m－2

表2 人员组成

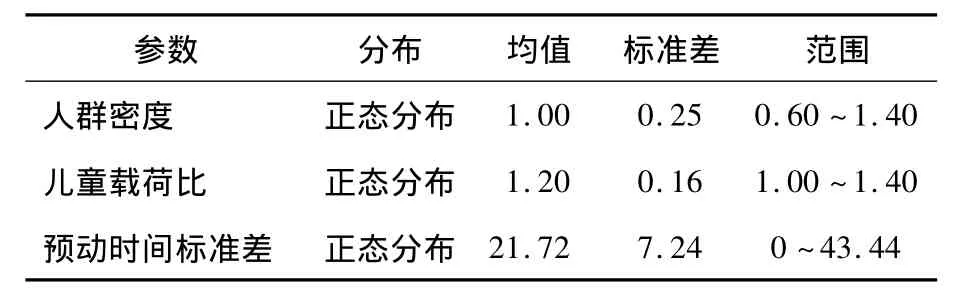
表3 不确定参数分布与范围

3.2.2 分析与讨论

为确定疏散时间多项式混沌展开T的收敛，分别抽取输入样本数为29和51构建其疏散时间T，按人群密度、儿童载荷比和预动时间的3阶和4阶进行混沌展开。为方便计算，本文基于所有数据拟合出人群密度与疏散时间关系曲线、儿童载荷比与疏散时间关系曲线、预动时间与疏散时间关系曲线。

1)人群密度与疏散时间关系

人群密度与人员的运动速度密切相关，人群密度越大，行人之间的距离越近，人员运动速度越小(见图3)。人群疏散速度与疏散时间有密切关系，疏散时间由步行时间和停留解除时间构成，疏散时间与人员运动速度的关系如图4所示，人群密度与疏散时间的关系如图5所示。

2)儿童载荷比与疏散时间关系

在人群疏散过程中，由于体质因素，老年人和儿童总是处于弱势。由于其行走速度较慢，故在紧急事件发生时容易滞留。另外，在紧急事件发生时由于受到其他人的作用，很难紧跟前面的疏散队伍。因此，不同的儿童载荷比对疏散时间有着密切的关系。图6为100人情况下不同儿童载荷比对疏散时间的影响。

图3 人员运动速度与人群密度关系曲线

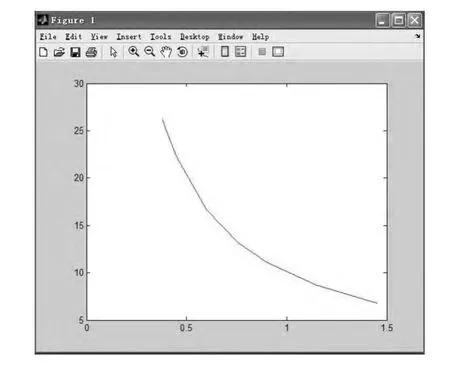
图4 人员运动速度与疏散时间曲线

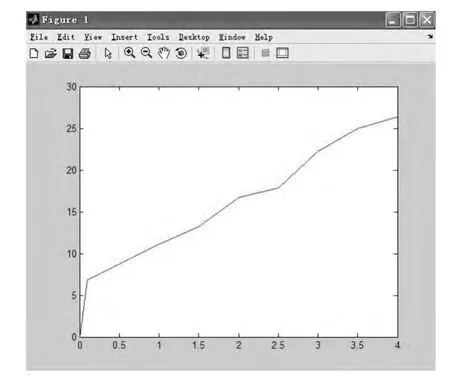
图5 人群密度与疏散时间曲线

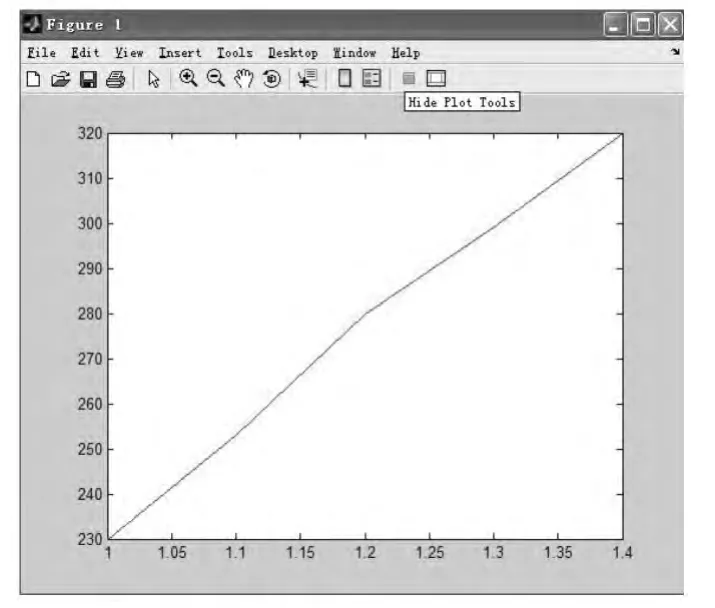
图6 儿童载荷比与疏散时间曲线图

3)反应时间与疏散时间关系

反应时间主要是人员确定紧急事件发生到响应的时间，由于人员的不同，反应时间也是不同的。根据不同人数反应时间的差异来分析反应时间对疏散时间的影响，如图7所示。

图7 反应时间与疏散时间曲线

4 结语

本文结合实例，利用多项式混沌展开进行了人群疏散时间不确定性研究，可得如下结论。

1)当人群密度低于1.1人/m2时，行人速度与人群密度呈非线性变化，人员的运动速度主要是由自身的特点决定，不受周围其他人的影响;当人群密度为1.1～2.6人/m2时，从有关图表可以看出人员速度与人群密度呈线性变化，所有行人的行为特征基本相同;从人群密度与人员疏散时间图表可以看出:当人群密度低于1.5人/m2时，呈线性变化;当人群密度大于1.5人/m2时，呈非线性变化。因此，在疏散和运营中应当合理控制区域间的人群密度。

2)疏散过程中，老人、儿童等不仅自身行走缓慢，而且会对整个疏散队伍产生不利的影响。因此，在疏散过程中应加强对此类人员的专项疏散引导和指挥。

3)在疏散人员相对较少，且人员的反应时间服从正态分布的情况下，反应时间对疏散时间的影响相比人员数量的影响较小;当反应时间相对较长时，人员的反应时间对疏散时间的影响较大，而人员数量造成的影响则较小。

因此，在具体设计人群密集区域疏散通道和相关产品、标识系统的时候，要充分考虑上述结论所涉及的内容，从而设计出高效、完美、人性化的区域疏散通道和相关产品、标识系统。

［1］宋彪，朱建明，黄启发．基于群集动力学和演化博弈论的网络舆情疏导模型［J］．系统工程理论与实践，2014(11):2984－2994．

［2］刘少博．人员疏散中个体和群体行为的实验和计算机模拟研究［D］．合肥:中国科学技术大学，2010．

［3］李俊梅，胡成，李炎锋，等．不同类型疏散通道人群密度对行走速度的影响研究［J］．建筑科学，2014(8):122－129．

［4］肖睿夫．考虑人员行为的火灾疏散时间的研究［D］．沈阳:沈阳航空航天大学，2015．

［5］张滨雅．步行设施空间特征与行人安全出口选择研究［D］．北京:北京交通大学，2015．

［6］屈云超．密集人群疏散行为建模与动态特性研究［D］．北京:北京交通大学，2015．

［7］郭雩．地铁车站火灾乘客应急疏散行为及能力研究［D］．湘潭:湖南科技大学，2012．

［8］胡玉玲，王飞跃，刘希未．基于ACP方法的高层建筑火灾中人员疏散策略研究［J］．自动化学报，2011(2):185－196．

［9］迟春见，于万波，魏小鹏．基于函数展开与超混沌系统的图像加密［J］．计算机工程，2011(8):146 －148．

［10］王小胜．不确定统计的若干问题及应用研究［D］．镇江:江苏大学，2010．

［11］锁斌．基于证据理论的不确定性量化方法及其在可靠性工程中的应用研究［D］．北京:中国工程物理研究院，2012．

［12］李慧颖，梁启宇，万千，等．基于行人过街场景的社会力模型改进研究［J］．交通信息与安全，2015(1):29－34．

［13］刘宇．基于风险的公共交通性自动扶梯安全保障技术研究报告［D］．西安:西安理工大学，2015．

［14］姚小林，陈俊敏．人员密度和出口宽度的不确定性对疏散行动时间的影响［J］．工业安全与环保，2014(10):50－54．