一种基于舰船辐射噪声起伏特性的线谱提取方法

张大伟，章新华，李前言，杨玉峰

(1．海军大连舰艇学院，辽宁 大连116000;2．中国人民解放军91329部队，山东 威海264200)

0 引言

舰船、潜艇、鱼雷所辐射的噪声，是被动声呐赖以探测、跟踪、定位、识别目标的重要依据［1］。研究表明，舰船辐射噪声由宽带噪声和离散的窄带分量组成，在频谱上表现为连续谱和线谱的叠加。其中，低频段线谱噪声中包含了稳定的舰船特征信息，同时也是现代降噪技术难以解决的问题，因此提取低频段线谱对于目标的探测和识别具有重要意义。

实际中，水听器接收到的信号是目标声源与海洋环境相互作用的结果。受到信号产生机理、声源与接收器相对运动、信号多途相干以及海洋表面风浪、温度微结构等因素的影响，到达接收水听器的目标信号具有一定的起伏性［2］。时域上表现为信号幅度和时延的起伏，频域上表现为幅度与相位随时间的起伏。

一般认为这种起伏性对信号的检测估计是有害的，需要通过平均、平滑等手段消除其不良影响。但美国Ronald A.Wagsaff等的研究指出，来自水下声源的信号具有低起伏性，表现为动态范围小，变化速率慢;而来自水面声源的信号以及海洋环境噪声具有高起伏性，表现为动态范围大，变化速率快;并据此提出了利用抑制高起伏噪声的非线性后置处理技术［3］。

受此启发，本文研究了舰船辐射噪声中线谱噪声、连续谱噪声频域上的起伏特性差异，提出一种舰船辐射噪声低频段线谱的提取方法。该方法回避了声信号起伏的不利影响，转而利用其特性差异做依据，为信号的检测估计做出积极贡献，大大改善了线谱的提取效果。

1 舰船辐射噪声的起伏特性

线谱噪声主要与舰船上机械部件的往复式运动、螺旋桨旋转、船壳体 (部件)共振等有关，其发声源惯性大，信号相对稳定。连续谱噪声主要来源于螺旋桨空化与机械噪声，受到舰船运动、海洋环境等因素影响较大，是舰船辐射噪声中不稳定的成分。文献［4－5］的研究结果指出，低频段的单频信号在海洋传输的结果让人满意，尤其是信号的相位具有“令人难以置信的稳定性”。叠加在低频段的线谱噪声具有更稳定的传输性能。可见，无论从信号的产生还是传输上，线谱噪声都具有相当的稳定性。

通过对大量舰船辐射噪声进行短时傅里叶分析，发现线谱噪声的这种稳定性，在频域上表现为幅度和相位随时间变化的低起伏性。信号处理流程如图1所示。

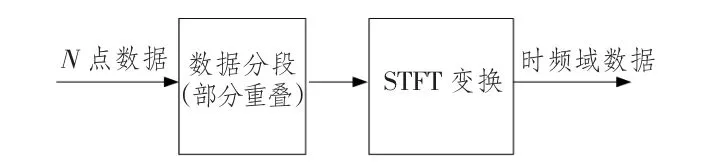
图1 信号处理流程Fig.1 The flowsheet of signal process

经过上述处理，将观察到的N点时域数据变换到时频域得到。随频率的变化反映了信号的频谱特性，而随时间的变化反映了信号频谱的时变特性。在某一频点上研究其对应的随时间变化的复数序列zi=riejθi(i=1，2，…，n)，发现该序列的幅度和相位角的随时间的起伏存在一定规律。下面将通过一个具有代表性的实例来说明。

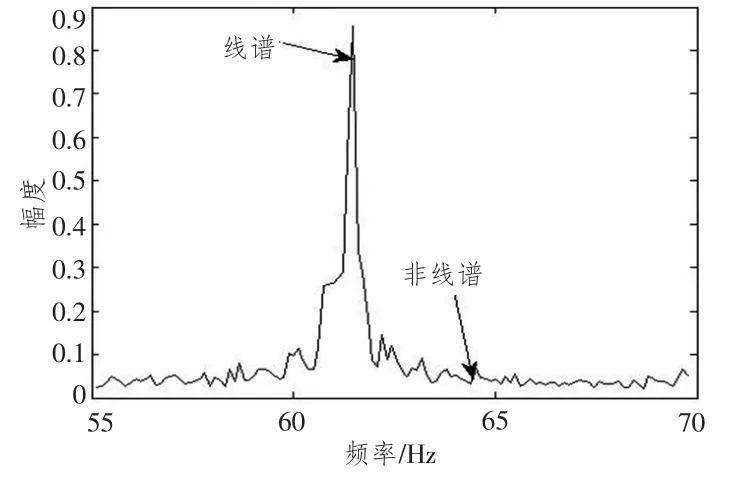
图2 某舰船辐射噪声的频谱Fig.2 The spectrum of the ship radiated noise

图2给出了某舰船辐射噪声在55～70 Hz间的频谱。可以看到，在62 Hz附近存在明显线谱。图3和图4将分别给出在图示线谱与非线谱处幅度与相位随时间的变化情况。

图3表明，线谱对应频点处幅度随着 (数据段编号，代表时间的变化)缓慢变化，波形不规则，局部动态范围小，具有低起伏性;而相位角的变化较快，波形呈大间隔的锯齿状，具有一定的规则性。这是由于声源与接收器的相对运动，信号的时延，信号处理过程等因素引起的。第3节将通过有效的相位均衡技术消除这种不良影响。

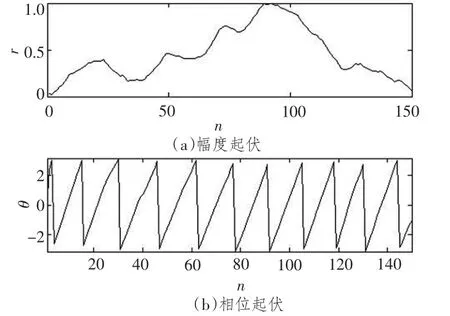
图3 线谱对应频点的幅度和相位随时间的起伏Fig.3 Fluctuations of amplitude and phase at the line-component spectrum

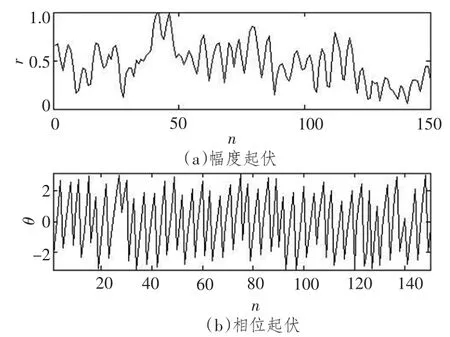
图4 非线谱对应频点的幅度和相位随时间的起伏Fig.4 Fluctuations of amplitude and phase at the continuous spectrum

图4表明，不存在线谱的频点处对应的幅度和相位随着数据段编号剧烈地变化，波形很不规则，局部的动态范围大，具有高起伏性。

至此，本文分别从理论和实测数据上得出结论:线谱噪声在频域上的幅度随时间的变化具有低起伏性，而相位随时间的变化具有一定的规则性，且二者相一致。

2 基于起伏特性提取线谱

2.1 相位校准

上一节的分析中指出，线谱对应频点处相位的变化表现出一定的规则性。文献 ［6］分析了影响信号相位角的因素，提出了一种相位校准 (APA)的技术。将相位角的变化看作是一种变加速运动，通过二次差分得到其加速度。当相位的运动具有规则性时，其加速度将近似为0;而相位的运动具有随机起伏时，其加速度将随机变化。

根据相位角θi的物理意义，将其表示为:

式中:x为声源与接收水听器间的距离;λ为波长;f为频率;t为时间;α为初始相位;β为由数据重叠分段和加窗等处理引入的相位变化。

定义相位加速度

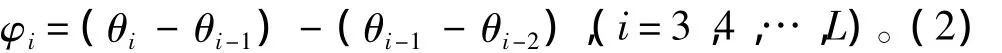
由式(1)可知，φi仅与声源和接收器相对运动的加速度变化有关 (实验表明，当数据分段重叠率满足一定要求时，β的影响可以忽略不计)。实际中，观察时间内舰船与接收器相对运动的加速度变化较小，从而使得φi的值接近于0。而在非线谱处，由于相位的随机性，使得校准后φi仍具有较大的分散的值。

为进一步提高估计的精确性和稳定性，本文将相位均衡的过程改进为取3阶差分，一方面使得校准后的结果对声源与接收器的相对运动更加不敏感，仅与加速度的变化率有关，另一方面通过差分加大了非线谱处相位随机起伏的趋势，使得起伏性差异更加明显。重新定义φi为

对图3与图4的相位进行校准后的结果如图5和图6所示。

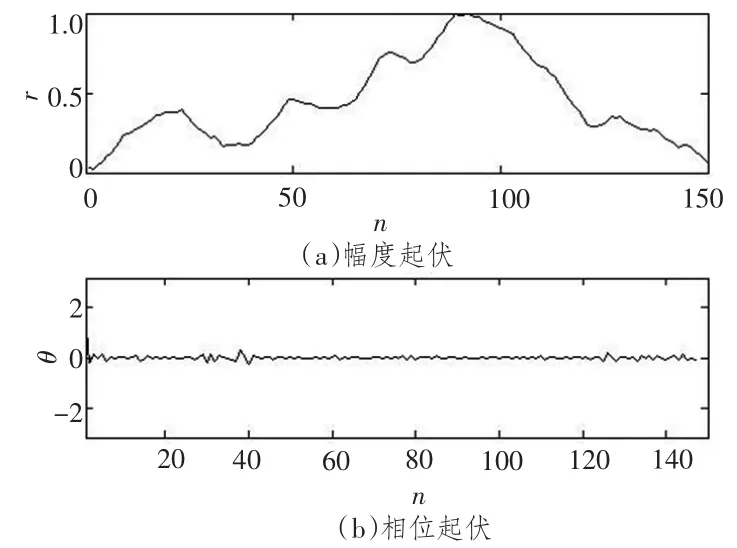
图5 线谱处相位均衡后的效果Fig.5 The result of phase aligned at the line-component spectrum

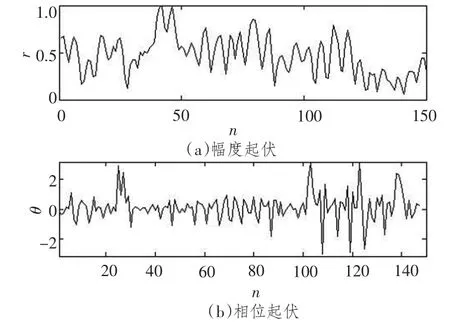
图6 非线谱处相位均衡后的效果Fig.6 The result of phase aligned at the continuous spectrum

从图5和图6给出的结果可看出，经过3阶差分校准后，线谱处的相位序列接近于0，而非线谱处的相位序列在较大的范围内快速变化。

2.2 利用起伏特性提取线谱

至此，经过以上分析和处理，本文基于以下原理自适应地提取线谱:频域中，若某一频点对应的幅度序列具有低起伏性且校准后的相位序列近似为0序列，则认为该频点处存在线谱，反之没有。

首先，定义相位因子

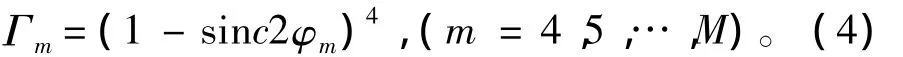
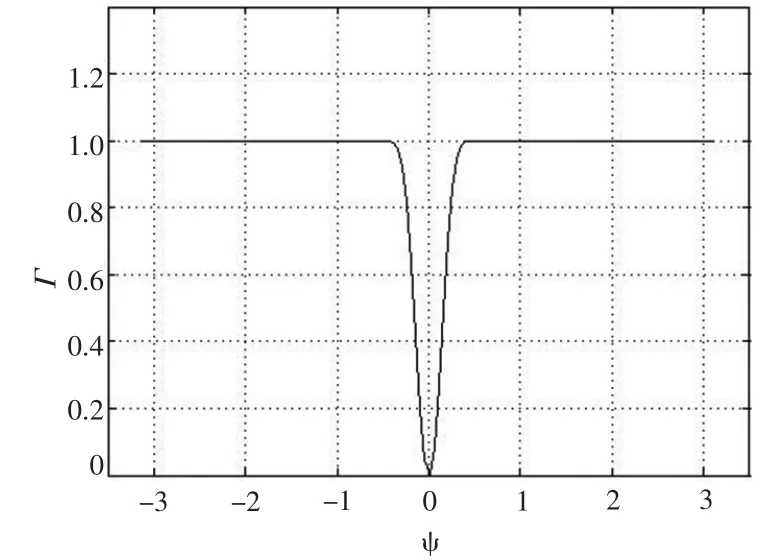
图7 F(φi)的函数曲线图Fig.7 the curve of F(φi)

图7给出了当φm在［－π，π］内取值时Γm的取值情况。该曲线表示，φm越接近于0，Γm也越接近于0。当φm偏离出0附近的窄小区间时，Γm将随着偏离程度的增大而急剧增大，并迅速稳定为1。

然后，利用得到的相位因子对幅度序列进行指数加权，保留线谱幅度序列基本不变，同时有效抑制非线谱的幅度 (为利用指数运算的单调性，需要对时频域上同一时间不同频率点的幅度值进行归一化处理)。定义指数加权后的序列为

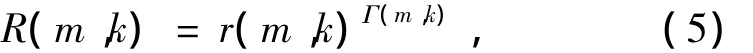
于是，线谱处具有较大的值，且保留了低起伏性，而非线谱处被抑制，且由于随机性地保留了少数较大的值而具有高起伏性。从而通过抑制高起伏噪声的非线性后置处理的方法，可以进一步抑制非线谱成分。该处理方法定义为

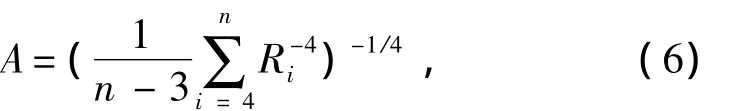
得到的频谱记为A谱。

接下来，利用均衡后的相位序列φi在线谱处接近为0且起伏缓慢的特点，可利用其方差的倒数对目标信号的频谱进行估计，定义为

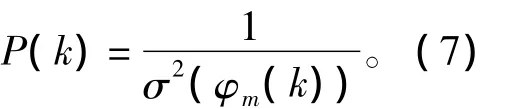
其中，σ2(φm(k))为均衡后相位序列φm的方差。得到的频谱记为P谱。

最后，由于A谱和P谱分别从不同的侧面反映同一目标信号的谱特征，其中的线谱信号具有相关性和一致性。于是将A谱和P谱对应的时域信号进行互相关处理，可进一步抑制宽带噪声，增强线谱。将互相关得到结果进行FFT分析得到目标信号的频谱，记为AP谱。

3 实验结果

使用实际测量的舰船辐射噪声数据对上述方法进行实验验证。数据采样率为25 000 Hz。下面分别对3类舰船目标进行10～200 Hz频段进行线谱提取，并将得到的结果与经典的Welch法进行比对。每次计算使用13.107 2 s长度的数据，数据分段的重叠率为0.98。为便于比较，对计算结果归一化后取对数，表示为分贝值。

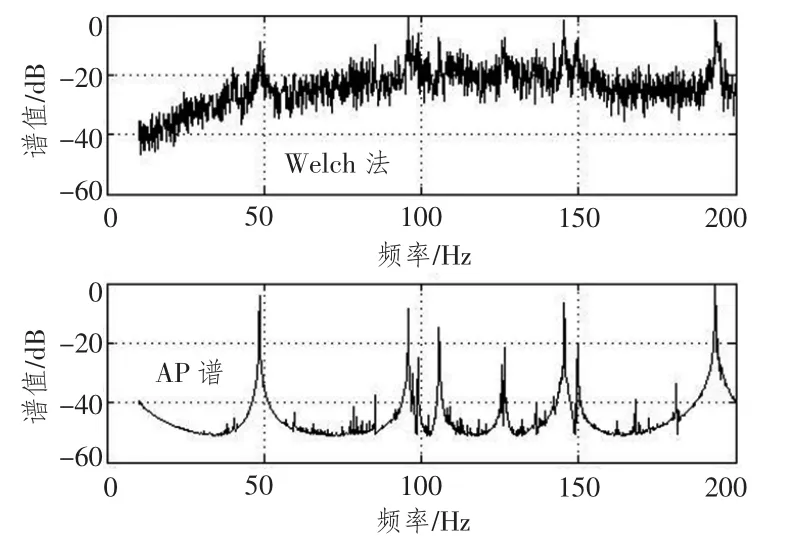
图8 A类目标的线谱提取结果Fig.8 The line-component spectrum of target class A

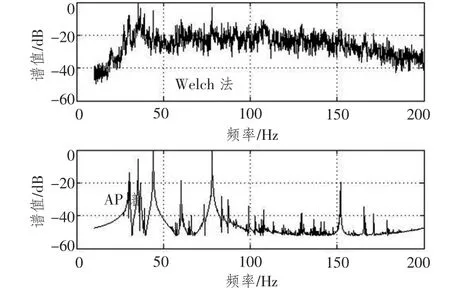
图9 B类目标的线谱提取结果Fig.9 The line-component spectrum of target class B

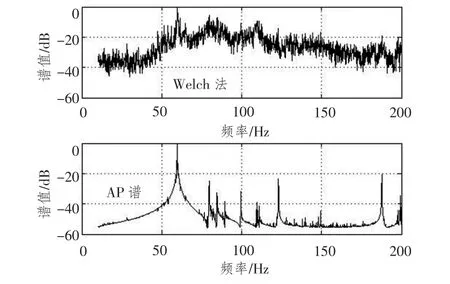
图10 C类目标的线谱提取结果Fig.10 The line-component spectrum of target class C

上面给出了A，B，C三类舰船目标的低频段线谱提取结果。图的上半部分表示使用经典的Welch法进行线谱提取的结果，下半部分给出了利用起伏特性进行线谱提取的AP谱结果。通过对比可以看到，本文提出的方法有效地抑制了频谱中的非线谱成分，进一步增强了强线谱，并使得淹没在宽带噪声中的弱线谱得以显现。某种程度上，AP谱的连续谱趋势得以自适应地去除，有利于线谱的自动检测和提取。同时，由于相位因子的指数平滑作用和互相关处理的筛选作用，使得谱线更加精细，提高了谱的频率分辨质量。

4 结语

本文研究了舰船辐射噪声频域幅度、相位随时间的起伏特性，利用线谱成分的低起伏特点，提出了一种提取低频段线谱的新方法。从3类舰船目标噪声实测数据的实验结果可得到以下结论:

1)本文方法用于A、B、C三类水下目标的低频段线谱提取均具有良好的效果，对目标信号的种类有较强的稳健性。

2)利用起伏特性的差异提取线谱，对舰船辐射噪声中的宽带噪声具有良好的抑制效果，且并不需要长时间的积分，便可达到令人满意的效果。

3)本文的计算以FFT分析为基础，在频率分辨率上受到FFT分析的理论限制。但作为一种后置处理方法，可结合现代谱估计技术对其进行更深入的研究。

［1］ 刘伯胜，雷家煌．水声学原理［M］．哈尔滨:哈尔滨工程大学出版社，1993．

［2］ 惠俊英，生雪莉．水下声信道［M］．北京:国防工业出版社，2007．

［3］ WAGSTAFF R A，LEYBOURNE A E，GEORGE J．“von WISPR Family Family Processors:Vol．1，”NRL/FR/7176－96－9650，Naval Research Laboratory，Stennis Space Center MS，Jul．，1997．

［4］ BURENKOV S V，GAVRILOV A N，UPORIN A Y，et al．Heard Island feasibility test:long－range sound transmission from Heard Island to Krylow underwater mountain［J］．J．A．S．A．，1994，96(4):2458 －2463．

［5］ WORCESTER P F，SPINDEL R C．North Pacific acoustic laboratory［J］．J．A．S．A．，2005，117(3):1449 －1510．

［6］ WAGSTAFFRA，GEORGEJ．“Phase variations in fluctuation based processors，”in Proc．SPIEAerospace/Defense Sensing Controls Symp．:Targets and Backgrounds:Characterization Representation II Conf．，vol．2751，Apr，1996:132 －141．