城际干线甩挂运输牵引车调度问题的模拟退火算法研究
2015-03-11李红启朱晓宁
李红启 卢 越 朱晓宁
1. 北京航空航天大学,交通科学与工程学院,北京100191
2. 北京华运交通咨询开发公司,北京100038
3. 北京交通大学,交通运输学院,北京100044
0 引 言
经济发达国家在20世纪60年代就已盛行借助汽车列车开展甩挂运输,该运输组织形式被广泛应用于城际干线运输、城市配送以及多式联运等领域。相对于卡车,汽车列车能够通过动力部分和载货部分的自由分离和结合而开展甩挂运输,从而获得更高的车辆使用效率[1,2]。
学术界普遍认为汽车列车的调度问题很复杂,是NP难题。迄今国内外学术界在甩挂运输汽车列车调度问题方面的研究成果主要体现为三类:(1)针对卡车与全挂车组合而成汽车列车调度的TTRP问题(the Truck and Trailer Routing Problem),研究成果以文献[3,4]等为代表;(2)针对城市垃圾运输过程的牵引车加挂半挂车组合而成汽车列车调度的 RRVRP问题(the Rollon-Rolloff Vehicle Routing Problem),研究成果以文献[5][6]等为代表;(3)针对厂内(局部)运输过程的牵引车加挂半挂车组合而成汽车列车调度问题,研究成果以[7][8][9]等为代表;以及针对城际干线运输过程的牵引车加挂半挂车组合而成汽车列车调度的TSRP问题,该类问题主要由文献[10]提出。
从调度作业对象看,甩挂运输车辆调度包括牵引车调度、载货半挂车调度、空半挂车调度和汽车列车调度等。本文定位于城际干线运输背景下的牵引车调度这一问题,建立一类公路牵引车调度问题数学模型,设计基于模拟退火的求解算法,并辅以实例分析。
1 问题描述
城际干线甩挂运输牵引车调度问题将分布于经济地理空间的城市抽象为网络节点、将城际高等级公路抽象为网络的边。城际干线运输网络的几乎所有节点间均可能存在货运需求,这种节点间的运输需求呈现为“多对多”的关系,与VRP问题中节点间运输需求的“一对多”关系[11]明显不同。
城际干线甩挂运输牵引车调度问题的基本特征如下:
(1)从能否保有牵引车角度知网络节点分为两类:中心场站和客户点。中心场站是唯一的,且保有大量牵引车,也是牵引车运行路线的始发终到点,牵引车不能长久停留于客户点;客户点的运输需求以载货半挂车为单元,任意两个客户点之间都可以有任意数量的运输需求。
(2)在甩挂运输模式中,牵引车连续工作时间与驾驶员工作时间之间联系密切。由于人体持续工作耐力、车辆行驶过程安全要求等因素,驾驶员法定工作时间是有硬性要求的。为合理利用牵引车乘组工作时间,每条牵引车运行路线的总运距在一个区间内,允许牵引车在同一运行路线中多次进出中心场站和某一客户点。牵引车的行驶状态只有两种:牵引车独自行驶,牵引车拖挂载货半挂车行驶。也即,本问题不考虑空挂车调配。
(3)牵引车、半挂车车型是同一的,且满足互换性和匹配性要求。设定牵引车独自行驶和牵引车拖挂载货半挂车行驶的平均速度为同一常量;设定牵引车独自行驶、牵引车拖挂载货半挂车行驶的百公里油耗量为常量;设定载货半挂车的额定载重量和货物实载率为常量。
(4)城际干线甩挂运输牵引车调度问题的求解目标是“吨公里CO2排放量”(单位:克CO2/吨公里),旨在明确甩挂运输车辆调度模式的效率和节能减排效果。依据联合国政府间气候变化专门委员会(Intergovernmental Panel on Climate Change)提供的CO2排放量计算方法,燃油消耗量与CO2排放量之间为确定的比例关系。
(5)货运需求满足率和车辆运行成本间体现为效益背反。对于某个物流运输企业而言,在合理权衡运输服务水平和运输成本时,有的货运需求可不予满足。也即,城际干线甩挂运输牵引车调度问题可要求货运需求满足率达到一定水平(不必为100%)。
(6)求解城际干线甩挂运输牵引车调度问题后,应能够确定所需要使用的牵引车总数及每台牵引车的运行路线方案,同时给出牵引车运行路线满意方案的“吨公里CO2排放量”。
能够确定城市节点间货运需求量是设计城际干线甩挂运输牵引车调度问题实践算例的基本条件。本文参照文献[12]提供的城际干线运量估算数据,以山东省17地市间货运活动为应用背景,抽象设计若干城际干线甩挂运输牵引车调度问题实践算例。在这些算例中,以17地市中的某一城市作为中心场站、其他16个城市作为客户点,可得到17个不同的算例。
2 求解算法的基本流程
借鉴既有针对TTRP问题和RRVRP问题等汽车列车调度问题求解算法的研究成果,本文采用模拟退火(SA)算法求解城际干线甩挂运输牵引车调度问题。SA算法被既有研究工作证明是可以成功解决汽车列车调度问题的一类启发式算法(如文献[5][13][14])。
2.1 可行邻域
SA算法可行邻域的构建过程如图1所示。牵引车运行路线的总运距要求是构造备选路线的基本依据。在对新算例进行试验时,采用“牵引车数量=货运需求总量/a”进行,其中a表示经验值。在重复模拟退火优化过程中增加牵引车数,使得满足率持续提高,可确定合适的牵引车数。

图1 可行邻域的构建Fig.1 Feasible neighborhood construction
2.2 基本流程
牵引车数量是SA算法的首要参数,求解结果与牵引车数量有很大关系。牵引车数量的确定方法包含最优牵引车数量Mbest的确定和最优牵引车路线方案的确定。以下是牵引车数量Mbest的算法求解流程:
Step 1 以经验值确定当前牵引车数量M;
Step 2 由可行邻域(V)中随机选取M条牵引车路线作为初始解X;
Step 3 设定初温T=T0,外循环计数变量w=0,内循环计数变量q=0,货运满足率为初始解X的货运满足率Rbest=R(X);
Step 4 外循环以自然数递增计数;
Step 5 内循环以自然数递增计数;
Step 6 从V中随机选取1条牵引车路线,替换X中随机1条牵引车路线后,生成新解Z;
Step 7 Metropolis准则判定(k为步长参数):若Δ=R(Z)-R(X)≥0,则将X替换为Z,即X=Z;若R(Z)-R(X)<0,设r为 0至 1之间的随机数,若exp(Δ×k/T)>r,则将X替换为为Z,即X=Z;
Step 8 计算当前路线方案Xbest下的Rbest,Xbest=X,Rbest=R(X);
Step 9 内循环终止判定:
内循环终止准则:达到设定的内循环次数。若在等温下q达到内循环次数Ne,即q=Ne,则进入下一次外循环,T计数,q置零,即T=T×k,q=0;若q Step 10 外循环终止判定: 外循环终止准则:达到外循环末温。若外循环未达到终止温度TF,即T-TF>0,回到Step 4;若T-TF≤0,终止SA算法外循环过程。 Step 11 牵引车数量的确定。R1和R2为拟达到的货运需求满足率边界。若货运需求满足率Rbest 牵引车路线方案的算法求解流程总体上与牵引车数量求解流程一致,不同之处是在Step 1直接取牵引车数为Mbest,此外,外循环终止判定准则有所差异。 下面为牵引车路线方案求解算法的伪代码示意。 Step 1: LetM=Mbest. Step 2: Generate the initial solutionXrandomly; Step 3: LetT=T0;w=0;q=0;Rbest=R(X); Step 4:w=w+1;q=q+1; Step 5: Generate a solutionYbased onX; Step 6: If Δ=R(Y)-R(X) ≥0, {LetX=Y;}Else {Generateγ= random (0, 1); If exp(Δ·w2/T) >γ, {LetX=Y;}} Step 7:Xbest=X,Rbest=R(X); Step 8: Ifq=Me, {T=τ·T;q=0;} Else {Go to Step 3;} Step 9: IfC(X) ≤C0,R(X) ≥ηandT-TF>0, {C0=C(X), Go to Step 3;}Else {Cbest=C0, Terminate the SA heuristics;} 依据牵引车运行路线的总运距要求所构造的备选路线总数决定了可行邻域规模,也决定了SA算法的求解效果。在本文所设计的山东省17地市间货运网络实例中,不同城市以其经济和交通区位特点决定了该城市作为中心场站的优势,也就决定了其作为中心场站时可行邻域规模上的差异。为扩展邻域,本文提出面向某一特定路线的复制操作:① 在初始备选路线中,找到各个牵引车路线所途经各个客户点的最大货运需求量Dmax;② 对各条路线,将其复制为Dmax条相同的路线,从而扩展了邻域。提出复制操作的主要理由是:根据牵引车运行路线总运距约束所构造的可行邻域中,每条备选路线都只在可行解中出现且仅出现1次,这可能导致在产生最终路线方案结果的模拟退火迭代过程中,某条牵引车路线出现多次的几率很低。但在企业的物流运输实践中,某条牵引车运行路线上可能有多台车辆并行运行。为此,以复制操作确保优秀的运行路线可被多次选中。 以济南作为中心场站的算例,复制操作前后可行邻域中牵引车路线总数分别为25 407条、73 610条,可行邻域规模扩充至原先的近3倍。本文仍以该算例进行试验:在相同的初温、末温、退火速度、内外循环规则、终止判别条件、迭代判别条件、步长规则等条件下,采用重复10次计算取结果的平均数来对比可行邻域扩展前后的求解结果(见表 1),可以发现增加复制操作环节有助于求解效果的改善。此外,增加复制操作环节时运算时间稍长。通过固定计算机软硬件配置来进行试验,当k取值为0.99时,有无复制操作的运算时间分别为123 s和108 s。 表1 采用复制操作与否的求解结果对比Tab.1 Results comparision of adopting copy operation or not k作为SA算法Metropolis准则的步长参数,其设定方式一般有固定步长和变步长两种情形。k的设定方式对SA算法的求解结果影响明显,步长决定了SA过程迭代前期是否能够快速跳出局部最优解和迭代后期是否能够快速获得全局最优解。 (1)以变步长k=w4(w为迭代次数)进行试验 Metropolis准则使一些迭代过程的更新解不会被采纳,在本文试验的4万余次迭代中,有750余次迭代过程的解被采纳(见图 2)。在该试验的前 100次迭代过程中,目标函数值以较快的速度降低至100g/(t·km)以下,而后续迭代中目标函数值的降低速度明显减缓。 图2 k=w4时被采纳的迭代过程Fig.2 The acceptable iterations when k=w4 (2)以固定步长k=104进行试验 当步长固定为 104次时,在相同的总迭代次数下,被采纳更新解的迭代数达到近 11 000次,说明Metropolis准则第二条被触发的次数远远高于k=w4的试验。取该试验最后1 000次被采纳更新解的迭代(见图3),最后1 000次迭代过程的解仍出现明显幅度的波动。 图3 k=104时被采纳的迭代过程Fig.3 The acceptable iterations when k=104 本文对步长设定规则做了一系列试验,试验主要涉及变步长和固定步长的多种取法,每种步长参数下重复运算10次并取平均值,结果如表2所示。可见,采用不同设定方式的变步长时运算结果波动较小,采用固定步长时的运算结果与步长参数设定的关系较为明显。在不同算例中,若采用固定步长,则需进行大量的试验来确定步长参数,本文建议以变步长作为步长参数(可取k=w3)。 表2 步长参数取值方式试验Tab.2 Tests of assignment of step-size parameters 对于SA算法内外循环过程对求解效果的影响,本文做了 3组试验,要求各组试验的总迭代次数相同,试验结果如表3所示。在相同的总迭代次数下,内循环次数越多则求解效果越差,且总迭代次数越少,这种现象越明显。依靠降温的外循环在向最优解趋近的速度上要快于内循环。本文建议采用无内循环的策略,以使运算过程在较短时间内完成。 表3 模拟退火过程内外循环试验Tab.3 Tests of inner and outer loop of SA 在对山东省城际干线甩挂运输网络算例进行求解时,货运需求满足率设定为不低于 85%。车辆方面,选取一汽集团生产的平头柴油半挂牵引车(型号CA4250P66K24T1A1HE)和山东鲁峰专用汽车公司生产的两轴厢式运输半挂车(型号 ST9351XXY)。车辆行驶速度定为50 km/h,牵引车拖挂半挂车行驶的油耗取为 32 L/100km,牵引车独自行驶的油耗取为18 L/100km。 在山东省的17地市中,有6个地市作为中心场站时可以达到100%的货运需求满足率,这些城市包括:济南、青岛、淄博、潍坊、泰安、莱芜。总体来看,这几个地市是交通区位较优、货源规模较大的城市。将货运需求满足率设为85%,则对17个算例的求解结果如表4所示(具体路线略)。 表4 货运需求满足率为85%时各算例牵引车调度方案求解结果Tab.4 Solving results of the tractor scheduling plan of all the instances when the satisfaction rate is 85% 除了以威海、菏泽为中心场站的算例外,其他算例的货运需求满足率均达到了 85%,吨公里 CO2排放量的平均值为78.11 g/(t·km)。该结果较现阶段山东省公路货运行业的吨公里 CO2排放量水平[15](约为135 g/(t·km)和我国公路货运业的吨公里 CO2排放量水平[16]明显要低。值得指出的是,本文研究工作是基于城际干线运输过程的公路牵引车调度算例进行求解,干线运输车辆吨位较大且运距较长,规模经济效应明显。 从本文经过求解获得的牵引车路线方案看,较为理想的牵引车路线往往是若干“一线两点,两端甩挂”模式的组合,这种组合过程更为复杂。可见,在较大规模的城际干线运输网络中开展甩挂运输,一般难以用传统的、人工调度方式确定牵引车调度方案。应高度重视城际干线运输牵引车调度工作的复杂性,并特别注重发挥各种物流信息化技术和人工智能决策技术的支持作用,尽量提高牵引车使用率和运用灵活性,科学设置驾驶员乘组方案;此外,要尽可能地将牵引车调度方案设计工作和牵引车场站选址、建设与运用环节有机结合。 城际干线货运是甩挂运输模式的主要应用领域之一,本文针对城际干线甩挂运输过程所用的公路牵引车的优化调度问题开展研究。该问题的基本特征包括:干线网络节点间货运需求为“多对多”式,货运需求以载货半挂车为计量单位,问题优化目标为吨公里碳排放量最小化。本文设计了基于模拟退火的求解算法流程,并借助山东省干线甩挂运输网络实践算例的求解试验过程,确定算法的主要运算策略:运用复制操作实现可行邻域规模扩展,采用变步长,只采用外循环。求解结果可同时确定牵引车数量、牵引车路线方案、优化目标函数值。后续研究工作可从多个角度展开,在模型方面如增加多场站条件、增加时间窗因素、增加半挂车流量平衡要求,等等;在方法方面可寻求求解效率和效果更好的混合启发式算法。 [1] Semet F., Taillard E. Solving real-life vehicle routing problems efficiently using tabu search[J]. Annals of Operations Research, 1993, 41(4): 469-488. [2] 李亚茹.提高道路运输效率的有效途径—— 甩挂运输[J].公路交通科技,2004,21(4):119-122. [3] Chao I.M. A tabu search method for the truck and trailer routing problem[J]. Computers and Operations Research, 2002, 29(1): 33-51. [4] Villegas J. G., Prins C., Prodhon C., Medaglia A. L.,Velasco N. A matheuristic for the truck and trailer routing problem[J]. European Journal of Operational Research, 2013, 230(2): 231-244. [5] Bodin L., Mingozzi A., Baldacci R., Ball M. The rollon–rolloff vehicle routing problem[J]. Transportation Science 2000, 34(3):271-288. [6] Baldacci R., Bodin L., Mingozzi A. The multiple disposal facilities and multiple inventory locations rollon–rolloff vehicle routing problem[J]. Computers& Operations Research, 2006, 33(9): 2667-2702. [7] 梁波. 大型钢铁企业厂内车辆循环甩挂[D].长沙:中南大学,2009. [8] 范宁宁. 烟大滚装甩挂运输牵引车调度优化研究[D].吉林:吉林大学,2012. [9] 张磊磊. LPG循环甩挂运输调度优化研究[D].大连:大连海事大学,2013. [10] Li H. Q., Li. Y., Zhao Q., Lu Y., Song Q. The Tractor and Semitrailer Routing Considering Carbon Dioxide Emissions[J]. Mathematical Problems in Engineering,2013, Article ID 509160, 1-12, http:// dx.doi.org/10.1155/2013/509160. [11] Barcos L., Rodríguez V., Álvarez M. J., Robusté F.Routing design for less-than-truckload motor carriers using Ant Colony Optimization[J]. Transportation Research Part E, 2010, 46(3): 367-383. [12] 高洪涛,李红启.道路甩挂运输组织技术及其应用实践[M].北京:中国物资出版社,2011. [13] Lin S. W., Yu V. F., Chou S. Y. Solving the truck and trailer routing problem based on a simulated annealing heuristic[J]. Computers and Operations Research, 2009, 36(5):1683-1692. [14] Lin S. W., Yu V. F., Chou S. Y. A note on the truck and trailer routing problem[J]. Expert Systems with Applications, 2010, 37(1): 899-903. [15] 北京航空航天大学,山东省交通运输厅. 山东省甩挂运输发展规划研究[R]. 2013. [16] Li H. Q., Lu Y., Zhang J., et al. Trends in highway freight transportation's carbon dioxide emissions and policies in China [J]. Energy Policy, 2013, 57,99-106.3 算法策略
3.1 复制操作
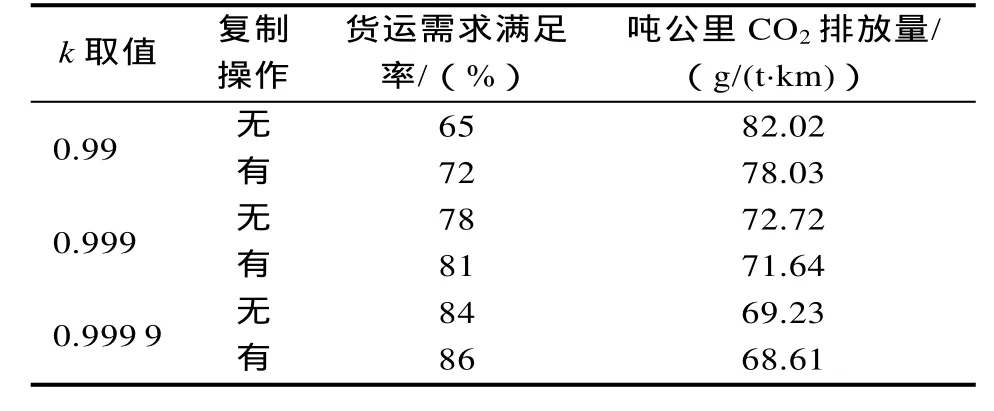
3.2 步长
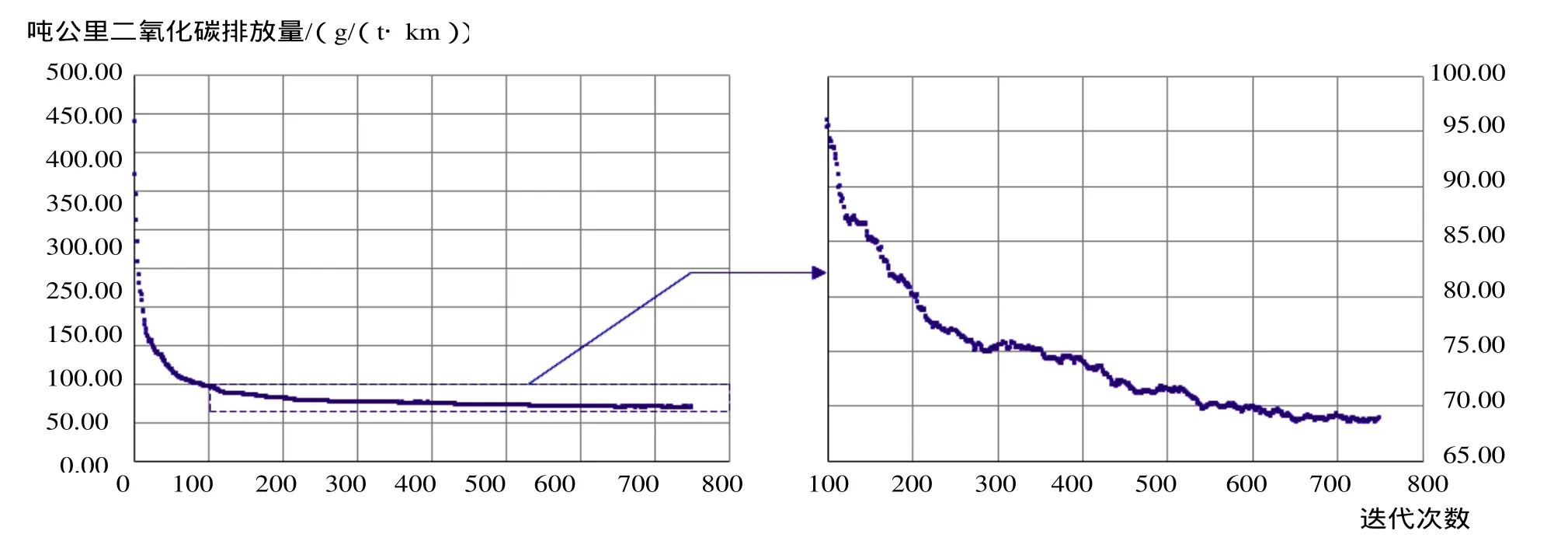


3.3 内外循环规则
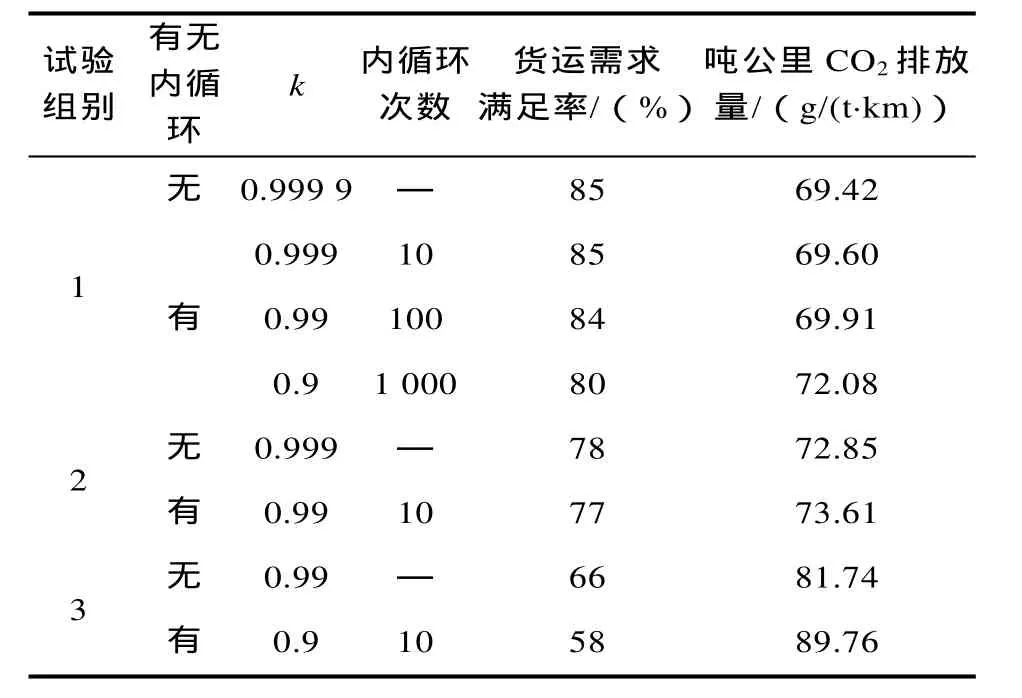
4 求解结果

5 结束语
