高一学生单调函数概念认知水平研究
2015-03-11朱立明马云鹏韩继伟王久成
朱立明,马云鹏,韩继伟,王久成
(1.东北师范大学 教育学部,吉林 长春 130024;2.东北师范大学 数学与统计学院,吉林 长春 130024;3.东北师范大学 附属中学,吉林 长春 130024)
高一学生单调函数概念认知水平研究
朱立明1,马云鹏1,韩继伟2,王久成3
(1.东北师范大学 教育学部,吉林 长春 130024;2.东北师范大学 数学与统计学院,吉林 长春 130024;3.东北师范大学 附属中学,吉林 长春 130024)
摘要:单调函数是高中数学函数部分的一个重要概念,它不仅有助于培养学生的抽象思维、逻辑思维以及创新思维,而且单调函数的图像还是数形结合思想方法的重要载体.用测试的方法研究高一学生单调函数概念的认知水平,发现大部分学生单调函数概念表征较为单一,对于单调函数概念的理解仅停留在表面,在抽象函数单调性问题上需要改进.
关键词:高中生;单调函数;概念表征;概念认知水平
1 问题提出
无论是基础教育还是高等教育,函数一直是数学的主线,也是整个数学教学的核心内容,而函数的性质在高中数学中占据重要地位,是历来各项考试的热点问题,作为函数重要性质之一的单调性,不仅应用极其广泛,而且还是数形结合思想方法的重要载体[1].查阅中外期刊文献,有关函数单调性解题及应用的综述很多,关于学生对单调函数认知方面研究很少,导致无法真正了解学生对单调函数的理解程度以及给学生学习带来的影响,基于此,研究主要以单调函数为具体内容,讨论高中一年级学生单调函数的认知水平.
2 研究的理论框架
从认知结构的建构观来看,数学概念理解是指个体在学习新概念的过程中,依据自身已有的数学认知结构对概念重新建构其意义,并使其成为整个数学认知结构的有机组成部分,从而逐步认识概念本质和规律的思维活动[2].根据布卢姆认知领域教育目标分类理论,将数学概念理解分为4个阶段:表征水平阶段、分析水平阶段、领悟水平阶段、应用水平阶段[3].同时,参考王晓辉的研究,将学生对单调函数的认知水平分为4个层次,(1)单调函数的表征水平;(2)单调函数的分析水平;(3)单调函数的领悟水平;(4)单调函数的应用水平.按照这个理论框架设计研究问题,分析学生单调函数的认知水平.
3 研究方法
3.1研究工具
按照研究的理论框架,以自编的调查问卷作为调查工具,问卷分3部分:第一部分为指导语;第二部分为学生的基本信息;第三部分为测试题;试题分为开放性试题、封闭式试题和半开放试题3种形式,旨在调查学生对单调函数的概念理解.问卷一共4道测试题目,其中第1题是关于单调函数概念表征的,第2题是关于单调函数概念分析的,第3题是关于单调函数概念领悟的,第4题是关于单调函数概念应用的.
3.2抽 样
研究样本选取长春市3所学校(重点学校1所和普通学校2所)选6个班级的学生进行调查,学校数量和调查对象人数见表1.

表1 学校数量和学生数
3.3研究过程
旨在了解高中学生对函数单调性的认知状况和存在的问题,主要采用问卷调查和访谈的方式进行研究.测试工具有:预测卷、正式测试卷和访谈提纲.根据自己的从教经验以及和一些专家教师与学生的交流,并查阅了大量的国内外关于单调函数的主要内容和各个研究角度的相关资料,进行整理、归纳而编制的.
在初步设计问卷的基础上,进行了预测,选取长春某校一个班的学生(30人)进行测试,根据学生答题情况对预测试卷中个别题目的难度进行修改,形成正式的调查问卷.又选取部分代表性的学生进行访谈,通过个别访谈了解学生答题时的思维过程,整理不能在问卷中反映出来的认知问题.对问卷进行修改,形成正式问卷.对所选样本进行实测.
4 结果分析
4.1高一学生单调函数各认知水平分析
4.1.1 表征水平分析
测试的第1题重点考察学生的表征水平,按照莱什(Lesh)在布鲁纳的研究基础上对概念表征的分类:书面符号表征、图形表征、实物表征、操作性模型表征和口头语言表征[4].根据学生的表现将学生的表征分为口头语言表征、图形表征、书面符号表征3类.学生在回答时表现出对单调函数概念的感知,分析学生的回答,从感性认识和理性认识两个层面上对单调函数加以理解,进而了解学生在表征阶段对数学概念理解的程度,见表2.

表2 单调函数表征阶段学生回答情况
研究结果显示:无论是重点中学还是普通中学,学生对单调函数概念的认知大部分以口头语言表征和图形表征的形式存在的,书面符号表征形式较少,值得注意的是符号语言表征形式中都能写出增函数(若x1
上述结果表明,学生对单调函数概念的表征形式是多种多样的,而不同学生的表征层次与学生的知识水平和学习经验有很大的关系,例如样本中重点高中学生书面符号表征所占比例是普通中学的二倍还要多,并且能够注意到概念中的区间性和任意性,而普通高中的学生多数采用图形表征形式,但更多学生仅仅画出增函数(一条递增的直线或曲线)和减函数(一条递减的直线或曲线)的图象,并没有针对图形对单调函数加以说明,图形表征还停留在表层阶段[6];部分学生对概念的口头语言表征是自己头脑中的概念意象,根据自己对概念的理解采用与概念相近的表象重新组织,导致概念意象与概念定义相互分离,甚至歪曲概念[7].例如在调查中发现,大部分学生以“y随x增大而增大,y随x增大而减小”作为陈述,更有学生错误地写道:“同一个函数中任意一项比前一项的函数值大的为增函数”.
4.1.2 分析水平分析
分析阶段包括要素分析、关系分析、组织原理分析3个亚类,通过将概念分解为各个组成部分,了解各个组成部分之间的相互关系和构成方式,从而掌握概念的属性[8].第2题考察学生对单调函数局部性的理解,函数单调区间与函数定义域之间的区别和联系.
根据调查结果将学生答案大体分成如下5类:标准类、区间错误类、单调错误类、特殊值验证类,见表3.

表3 单调函数分析学生回答情况

由于数学的抽象性,使利用数学符号表征单调函数概念成为必然[9],而抽象的符号定义给学生的理解带来阻碍,尤其是单调函数中x1、x2的任意性、单调区间的局域性以及单调区间与函数定义域之间的关系.在访谈中一位学生说:“受到原来的初中的正比例函数的影响,总是以为函数(图象)都是一直上升的,所以根本没有考虑到单调区间.”学生在原有认知基础上,将单调区间与定义域视为同一个概念,从而导致错误的出现;除此之外,更多学生将单调区间采用并集的形式表示出来,也是单调函数初学者常见的一种错误.
4.1.3 领悟水平分析
领悟阶段包括转化、解释、推断3个亚类,是对于所学过的知识的意义的把握.美国心理学家奥苏泊尔(D. P. AuSubel)提出一种概念同化的学习形式,即新信息与原有认知结构中的有关概念相互发生作用,实现新旧知识的意义的同化,从而使原有的认知结构发生某些变化[10].第3题、第4题主要考查学生对于单调函数概念的形式转化以及推断能力,主要体现领悟单调函数所蕴含的数学思想(数形结合思想、分类讨论思想、转化思想),具体情况见表4.

表4 学生对数学思想领悟情况
结果显示,只有63.46%的学生可以利用单调函数概念实现本题的转化,不足70%,22.12%的学生直接给出正确答案,而采用特殊值验证方法的学生占7.69%,采用分类讨论方法的接近50%,而采用图象法的只有17.31%;在图象法中,只有22.22%的学生提出数形结合思想,有55.55%的学生能够正确画出分段函数的图象;在分类讨论方法中,只有18.75%的学生提出分类讨论思想,而解集没有与定义域进行交集运算的高达31.25%.与重点中学相比,普通中学的学生更多采用图象的方法,数形结合的方法略优于重点中学,而能够利用单调函数转化的要比重点中学低很多.
钱珮玲在《数学思想方法与中学数学》中指出了数学思想和数学方法之间的区别和联系,数学方法是处理问题的手段、途径,而数学思想是“对数学知识的本质的认识,是从某些具体的数学内容和对数学的认识过程中提炼上升的数学观点,它在认识活动中被反复运用,带有普遍的指导意义,是建立数学和用数学解决问题的指导思想”[11].而美国心理学家布鲁纳(J. S. Bruner)认为:“不论我们选教什么学科,务必使学生理解该学科的基本结构.”调查发现,学生缺乏对数学思想的认识和提升,没有领悟处理问题过程中所蕴含的数学思想(分类讨论思想、数形结合思想),导致学生对问题的理解仅仅处于表面阶段,不能深入其本质.正如一名学生说:“我只知道是分情况来做,老师讲的就是这样,至于为什么,我不是很清楚.”解题训练作为一种教学法,其机制并不只是让学生接触,熟悉和记住解题技能和技巧.运算、操作是数学思维发生之处,是完整概念形成的基石,它为学生理解领会提供了必要条件[12].因此,只有以数学思想作为指导思想,才可能在解决问题中不但知其然,还能知其所以然.
4.1.4 应用水平分析
应用阶段是学生将所学概念应用到新的情境中去,运用它解决同类问题的阶段.概念的应用有知觉水平上的应用和思维水平上的应用两个层次,知觉水平上的应用是指学生在获得同类事物概念以后,当遇到这类事物的特例时,能够将其视为这类事物中的具体例子;思维水平上的应用是指学生学习的新概念被类属于水平较高的原有概念中,新概念的运用必须对原有概念重新组织和加工,以满足解决当前问题的需要[13].如果说第2题属于知觉水平的应用,那么第4题就是考察学生思维水平上的应用,需要学生利用抽象思维,实现对单调函数从一种认识状态(具体函数)到另一种认识状态(抽象函数)转变的意识[14].
比格斯(Biggs)基于皮亚杰认知发展阶段论提出的SOLO分类评价法,将学生学习的结果由低到高分为5个不同的层次,即:前结构(prestuctural)、单点结构(unistructural)、多点结构(multistructural)、关联结构(relational)、拓展抽象结构(extended abstract)[15].借助SOLO分类评价法将学生答题结果分为3类,未解决类(前结构、单点结构、多点结构)、已解决类(关联结构)、拓展类(拓展抽象结构)[16],具体情况见表5.
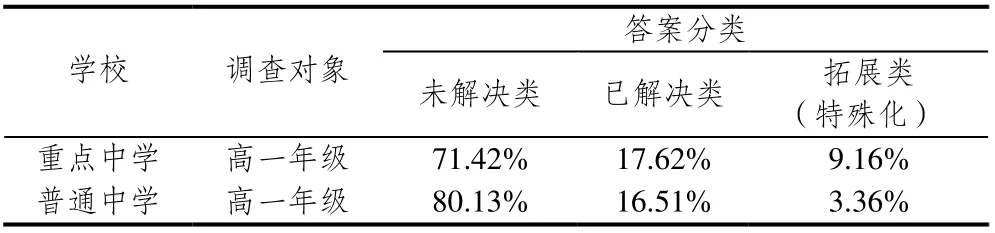
表5 单调函数应用水平学生回答情况
上述结果显示,从整体看本题的解答,重点中学的学生相对要优于普通中学的学生,但是更多学生只能达到前3个结构层面,不能将问题解决,重点中学占71.42%,均超过60%;而达到关联结构层面能够将问题解决的学生仅有17.62%,能够达到拓展抽象结构层面举出函数特例的学生还不足10%.抽象函数没有具体的表达式,只表现出一定的对应法则,满足一定的性质,因学生此在处理此类问题时由于匮乏对函数性质的理解,加之抽象符号的干扰,
难以将题目中的条件融会贯通,建立“条件网”.正如一名学生说:“初中数学也可以,当上高中后每次做抽象函数题,没有一点思路,不知道题意,不知道怎么下手.”
4.2学生认知水平的整体
下面从整体水平对两类学校所选样本进行分析,具体结果见表6.

表6 4种水平阶段分析结果
调查显示,对单调函数理解达到表征水平阶段(至少能够使用一种表征形式)重点中学学生占88.5%,普通中学学生占86.2%,均超过60%,而且两类学校差异不大.对单调函数理解达到分析水平阶段(能够正确说出单调区间和函数单调性)重点中学占9.76%,普通中学占5.88%,均不到10%,而重点中学几乎是普通中学的两倍.对单调函数理解达到领悟水平阶段(能够明确写出思想方法)重点中学占26.04%,普通中学占14.12%.对单调函数理解达到应用水平阶段(能够正确写出答案或进行适当拓展)重点中学占26.78%,普通中学占13.87%,对于后3种水平阶段,重点中学达到比例接近是普通中学的两倍.
从整体看,学生对单调函数的理解更容易达到表征水平阶段,而达到分析水平阶段的学生,虽然重点中学明显高于普通中学,但均不到10%,达到领悟水平阶段和应用水平阶段的学生比例有所升高,但是均不到30%,而且重点中学接近于普通中学的两倍.可见学生对单调函数概念的分析不够深刻,可能是导致领悟数学思想和应用受到阻碍的一个原因.
表征水平阶段对后面3个水平阶段存在制约作用,以表征水平阶段对应用水平阶段的影响为例进行说明,见表7.

表7 表征水平阶段对应用水平阶段的制约
结果显示,能够使用3种表征形式描述单调函数概念的学生所占比例,与应用水平阶段达到拓展层面学生所占比例吻合.此外还发现,使用图形表征形式的学生,在处理问题时更多使用的是函数图象的方法,而使用口头描述表征的学生,在处理问题时更多使用特殊值或验证的方法.数学概念的理解程度应该取决于5种表征之间关联的丰富性、稳定性、强度与自洽程度,因此部分表征类型的缺失也可能是妨碍学生对数学概念理解的一个重要原因.
5 讨论与结论
5.1讨 论
以学生对单调函数概念认知为视角,分别从表征水平、分析水平、领悟水平、应用水平4个阶段分析学生对单调函数的理解程度以及单调函数的学习给学生带来的影响,从而得出一些结论.研究具有一定的局限性,这里仅选用一所重点学校和两所普通学校中316名学生进行测试,样本较小,仅分析学生对单调函数的认知,并未考虑教师因素(如教师的专业知识、不同成长阶段的教学经验、教学风格等)对学生认知单调函数所造成的影响,当然,这些因素也超出研究范围.
调查显示,学生的理解水平不高,因此应将如何提高学生水平作为教学活动中的重要环节.受传统的观念影响,把课程视为学科逻辑系统组织的教学内容,基于数学学科本身具有高度的抽象性、严谨的逻辑性、应用的广泛性、内涵的辩证性等特征,学生接受起来明显偏难,而数学概念又是核心内容,因此通过提高教师的MPCK,使其能够在概念理解的处理上发挥最大作用,从而寻求学生原有认知结构和外部知识逻辑体系有机结合的切入点,在组织课程的时候将重点置于学生学习内容与学习经验之间的有机联系,培养学生从多种表征形式理解数学概念的整体性,强调抽象函数特例化解决的一般函数方程思想,注重加强学生的数学符号意识.
随着年级的提升,学生的综合能力可能会不断增强,因此提出可以在教学中采用螺旋式课程组织形式,在不同阶段重复学习原有的主要概念和观点的深度和复杂程度,试图建立学习内容逻辑关系和学生认知心理之间的联系.
在教学中需要侧重数学思想方法的培养,尤其高一年级的学生,领悟数学思想是目前容易忽略的问题,通过提升学生的数学思想,培养学生理解数学问题中条件和问题之间的内在联系,从而达到触类旁通,事半功倍的效果.
5.2结 论
(1)学生对单调函数概念的表征形式主要集中在口头语言表征、图形表征、书面符号表征3种形式,而不同学生的表征层次与学生的知识水平和学习经验有很大的关系.书面符号表征,容易忽视区间性和任意性;图形表征更多还停留在表层阶段;而口头语言表征大部分是学生头脑中的概念意象.
(2)高一年级的学生缺乏单调函数局域性的认知,对于函数的定义域与函数单调区间容易造成混淆,难于理解函数的单调区间是函数定义域的子集,更多学生直接将两个概念视为等价关系,极易用并集表示函数的单调区间.
(3)高一年级的学生缺乏对数学思想方法的领悟,在解决问题中更多关注问题处理过程中的方法和手段,很少能够上升到思想层面,因此在问题解决中缺乏指导思想,亟待改善.
(4)高一年级大部分学生受思维定式的影响,对单调函数的理解仅仅局限于表面,在处理问题时更多停留在前结构层次和单点结构层次,习惯具体、有形的解析式,对单调抽象函数的把握依然是难点,数学中的抽象函数依然是学生的弱点,抽象思维有待提高.
(5)学生对单调函数概念的理解更多停留在表征水平阶段,在表征水平阶段更多学生使用单一的表征形式,这可能是妨碍学生理解单调函数的一个原因;达到分析水平阶段的学生所占比例很小,这可能会阻碍达到领悟水平阶段和应用水平阶段.由此可见,在单调函数概念的教学中,应加强重视学生表征水平阶段和分析水平阶段的达到程度.
[参 考 文 献]
[1]刘祖望.中等数学中的函数单调性[J].重庆教育学院学报,2004,(3):15-17.
[2]李莉.学生学习数学概念的层次分析[J].数学教育学报,2002,11(3):12-15.
[3]贾丕珠.函数学习中的六个认知层次[J].数学教育学报,2004,13(3):79-81.
[4]Grouws D A. Handbook of Research on Mathematics Teaching and Learning [M]. New York: Macmillan Publish Company, 1992.
[5]李善良.关于数学概念表征层次的研究[J].数学教育学报,2005,14(4):35-37.
[6]曾国光.中学生函数概念认知发展研究[J].数学教育学报,2002,11(5):99-102.
[7]罗新兵,罗增儒.数学概念表征的初步研究[J].数学教育学报,2003,12(2):22-23.
[8]柳海民.教育学原理[M].北京:高等教育出版社,2011.
[9]黄翔.数学课程标准中的十个核心概念[J].数学教育学报,2012,21(4):16-19.
[10]王晓辉.数学课程与教学论[M].长春:东北师范大学出版社,2005.
[11]钱佩玲.数学思想方法与中学数学(第二版)[M].北京:北京师范大学出版社,2008.
[12]李士锜.熟能生巧吗[J].数学教育学报,1996,5(3):46-50.
[13]濮安山,史宁中.从APOS理论看高中生对函数概念的理解[J].数学教育学报,2007,16(2):48-50.
[14]李吉宝.数学概念教学应该帮助学生形成七种数学观念[J].数学教育学报,2011,20(2):88-89.
[15]Biggs J B, Collis K F.Evaluating the Quality of Learning——The SOLO Taxonomy [M].New York: Academic Press, 1982.
[16]陈蓓.利用SOLO分类法探究学生函数概念理解水平[J].数学教育学报,2009,18(2):35-38.
[责任编校:周学智]
Study of Cognitive Level of the Concept of Monotonic Function of High School Students
ZHU Li-ming1, MA Yun-peng1, HAN Ji-wei2, WANG Jiu-cheng3
(1. Northeast Normal University Faculty of Education, Jilin Changchun 130024, China; 2. Northeast Normal University School of Mathematics and Statistics, Jilin Changchun 130024, China; 3. High School Attached To Northeast Normal University, Jilin Changchun 130024, China)
Abstract:Monotonic function is an important concept in function of high school mathematics. It not only helps to cultivate the students’ abstract thinking, logic thinking and creative thinking, but the image of monotonic function is also the important carrier of thought of symbolic-graphic combination. Using the method of testing to do research on cognitive level of the concept of monotonic function of high school students, it is found that most of the students’ representation of the concept of monotonic function is relatively single. Their understanding of the concept of monotonic function is shallow and the monotonicity of abstract function needs improvement.
Key words:high school students; monotonic function; representation of concept; cognitive level of concept
作者简介:朱立明(1986—),男,河北承德人,东北师范大学教育学部在读博士,主要从事课程与教学论方面研究.
基金项目:教师教育协同创新中心总体设计的合作研究重大项目“高素质教师成长规律与培养方式变革研究”下的重点研究课题——教师教育创新课程开发与教学设计(XTZX20130002)
收稿日期:2015-03-04
中图分类号:G420
文献标识码:A
文章编号:1004-9894(2015)04-0061-04
