教学与科研相结合原则在偏微分方程数值解教学中的实践

黄鹏展

（新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830046）

教学与科研相结合原则在偏微分方程数值解教学中的实践

黄鹏展

（新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830046）

摘要：教学与科研相结合原则是高等教育原则中较为重要的一条.当前对大学生创新能力要求的提高，就更突显这条原则的重要性.通过在偏微分方程数值解教学中对这条原则进行教学实践，可以发现对这条原则的应用，不仅可以开拓老师的科研视野，扩大科研资源和思路，而且可以增强学生的学习兴趣，发展其创造性思维.

关键词：教学与科研相结合；偏微分方程数值解；创新；高等教育原则

1　引 言

教育原则，简单地说，是指一切教育活动应该遵循的基本准则[1].早在古代，人们就开始总结教学实践经验，探讨教学过程兴废成败的原因和条件，并提出了各种教学工作中的要求.到了近代，教育家们明确提出了教育原则这一概念，制定了一系列在当时有益于教和学的教学原则.而17世纪捷克教育家J·A·夸美纽斯《大教学论》（1632）的问世则确立了它在教育学理论中的重要地位.

教育原则按对象分，主要可以划分为基础教育原则与高等教育原则.早期出现的一些教育原则一般都是基础教育原则.高等教育原则是在基础教育原则的基础上产生，并且不同于后者，各有其自身的特点，但是两者都是通过教育过程培养人，只是具体培养目标不同.比如量力性（可接受）原则，在小学课堂教学中得到广泛应用，但在高等学校的教学实践中则并不提倡.同样地，科学性与思想性相结合的教学原则在大学课堂上，教师应用得比较多；而在中小学的教学中就不见得怎么应用.相比于后者，对前者的研究还比较短暂，整个高等教育领域研究在国际范围内是从20世纪50年代才陆续开始的[2].

国内外众多的学者提出了一系列的高等教育原则.其中，教学与科研相结合原则是一条较为重要的原则.这里主要探讨这一高等教育原则，进而研究在偏微分方程数值解教学中，如何利用该原则来培养大学生探求新知识和科学创新的能力.

2　教学与科研相结合原则

教学与科研相结合的教育原则是指在高等学校的教学中，要求大学生在学习知识的同时掌握科学研究的方法，发展科学研究的能力，培养科学精神、科学态度与科学道德，通过科学训练提高他们的创造能力与学术水平[2].早在19世纪初，德国教育家W·F·洪堡就提出了教学与研究相统一原则[3~4].

此后，教育家们在研究高等学校教育原则的时候，都提到了这条重要原则.比如，出现在苏联科贝里利亚茨基的《高等学校教育原理》9条高校教育原则中；中国潘懋元的《高等教育学》10条高校教育原则中；于美方的《大学教学论》5条高校教育原则中；钱伯毅的《大学教学论》5条高校教育原则中；薛天祥的《高等教育学》6条高校教育原则中；钱佩玲的《在大学数学教学中应注重贯彻“教学与科研相结合”的原则》6条高校教育原则中[5]；张亚丽的《我国高等学校教学原则体系的科学构建》8条高校教育原则中.虽然他们主张的高等教育原则各有不同，但是他们对教学与科研相结合这一教育原则却抱着相同的态度.

教学与科研两者是相辅相成、互相促进的.一方面，科研对教学具有积极的促进作用.洪堡提倡的科研就是为了使研究成为教学的一种手段，这是他最早提出教学与科研相结合这条原则的本意.早期大学里的科研就是为了更好地服务教学.目前，随着科学技术的不断发展，教学手段的改进远远满足不了教学改革的需要.这就要求研究者们通过科学研究来深化教学内容改革；来提高教师的理论研究能力，开拓知识视野和提升教学水平.最后应及时地把科研成果转化到教学中去，进而能更好地在教学中提高大学生的学习兴趣，培养大学生探求新知识和科学创新的能力.另一方面，教学对科研也起到有益的补充和促进作用.深入细致的教学工作能为科研开辟更为广阔的科研主题，而在教学过程中经常引入和介绍一些前沿的科研成果则更能为科研提供新的思路和想法.同时，在为大学生授课时，由于他们接受新鲜事物和想法比较快，故而老师经常可以在学生身上接触到一些新知识，从中得到启发，为科研提供新的资源和灵感.

3　偏微分方程数值解教学中的实践

偏微分方程数值解是数值分析的后继课程，它是一门具有较强实际背景、专门研究科学计算的课程，是信息与计算科学专业本科生必修的专业课程.作为数学类的传统专业课，这门课的知识点成熟，逻辑性较强，涉及的内容丰富，很适合教学与科研相结合这条高等教育原则的实践.

那么，在偏微分方程数值解教学中，教学与科研相结合原则实践应该怎样具体体现呢？要收到较好的教学效果，进而培养大学生探求新知识和科学创新的能力，必须把握教学与科研相结合教育原则的基本理念并结合偏微分方程数值解课程自身的特点，从不同的角度，比如科研对教学的促进作用、教学对科研的补充和促进作用，深挖相关概念产生的理论、经验与应用背景.相关案例的选择要有鲜明的教学和科研目的性，要展现从现象到本质的教学效果，以及活跃的科研思维.

新疆大学数学与系统科学学院采用偏微分方程数值课程的教材是陆金甫和关治编著的《偏微分方程数值解》[6].下面选取该教材中的例子作为偏微分方程数值解教学中教学与科研相结合原则实践的教学案例.

3.1教学对科研有促进作用的教学案例

在文献[6]中的第三章，讲到了一阶线性常系数双曲型方程的有限差分解法.该教材主要针对对流方程构造了多种差分格式.

考虑一维区域上对流方程初值问题

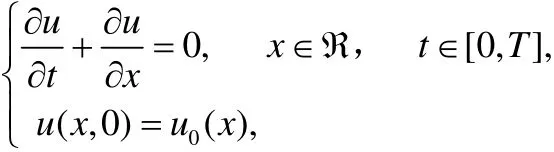
其中

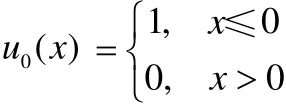
取空间网格步长h=0.01，网格比l=0.5，运用Lax-Wendroff格式和Beam-Warming格式来计算至tn=0.5时的数值解，初值问题的解析解与计算结果见图1，实线为精确解，虚线为数值解.这里的Lax-Wendroff格式如下：

Beam-Warming格式为

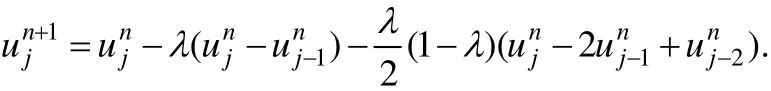
这两个差分格式都是2阶精度的显示格式.

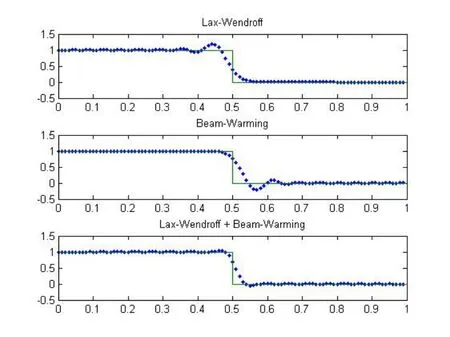
图1　3种差分格式的离散解

从图1可以发现Lax-Wendroff格式和Beam-Warming格式得到的数值解都在间断处产生虚假的振荡.更有趣地是，两种格式所产生的数值振荡出现关于点(0.5, 0.5)中心对称的现象.

以上内容，在教学过程中都会给学生讲到.事实上，一般的授课也就会到此为止.但是如果进一步去研究其本质的话，就会发现一种分辨率更高的新的差分格式.这为科学研究提供很好的问题来源.

利用文献[7]中的余项效应分析方法，可以知道数值振荡是由差分格式的数值色散性引起.通过计算两种格式的色散主项，发现Lax-Wendroff格式的色散主项小于0，格式为逆色散格式；Beam-Warming格式的色散主项大于0，格式为正色散格式.进而，从图1可以看到Lax-Wendroff格式在间断上方振动，Beam-Warming格式在间断下方出现振动.

事实上，研究者发现由于两种格式色散主项一正一负，从而产生的数值振荡一个在上方一个在下方，且恰好是中心对称的，那么自然想到能不能把这两个格式做加权平均，这样能否抵消一些数值色散性，从而减弱格式的数值振荡.把两种格式相加后 再做平均得到一种新的格式，记作Lax-Wendroff+Beam-Warming格式，如下

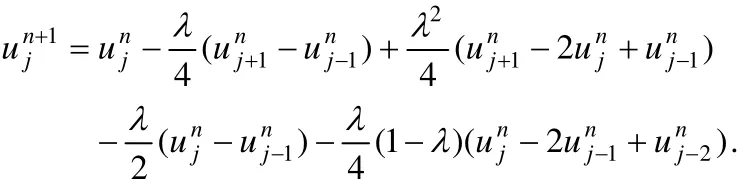
该格式得到的数值结果见图1中的第三个子图.可以观察到，由文献[6]中两个差分格式产生的数值振荡已经大大减弱.这是由于色散主项在加权平均下变小，从而振荡减弱.

通过这个教学案例，可以发现在教学过程中老师是给学生在讲解对流方程的几种有限差分格式.实际上，由于老师的知识积累，了解到了一些更深层的差分方法内容.所以，当研究者在上这部分课时，发现到图1中最上两子图的数值解有中心对称性.这引起了研究者的注意和兴趣，进而对格式本质进行探索.通过大胆猜测小心求证，得到了一个精度较高的数值格式.这恰恰说明了教师通过教学给学生传递知识，同时也在教学过程中获得了科研工作中所需的资源和灵感.进而可以影响大学生去探求新知识，潜移默化他们的科研态度和素养，提高他们科学创新的能力.

3.2科研对教学有促进作用的教学案例

新疆大学数学与系统科学学院采用陆金甫和关治编著的《偏微分方程数值解》[6]前面几章是有限差分方法的内容，后面三章介绍了有限元方法.其中，第五章介绍了Poisson方程的差分格式；第八章给出了该方程的线性有限元方法.

考虑d维区域上Poisson方程第一类边值问题

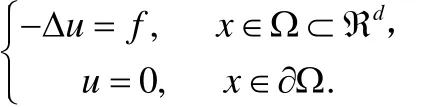
当d1=时，我们有差分格式

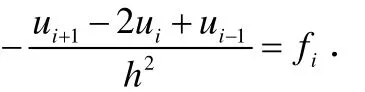
其中h 为网格步长，fi=f(xi).

而采用线性有限元方法来数值求解该问题，一般可以分五步.第一步，给出问题的变分形式.即只须方程两边同时乘以一个任意的检验函数v，再进行分部积分得

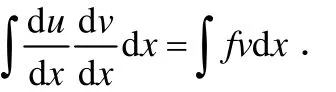
第二步，对区域进行网格剖分.网格尺度与差分方法一致.第三步，构建有限元空间.取一次多项式空间作为有限元空间.第四步，给出有限元格式，如下

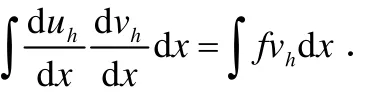
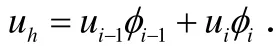
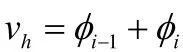
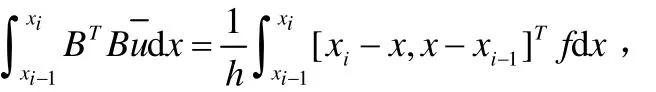
其中，

以上用两种方法构造了原问题的数值格式，接下来就是编程计算，事实上教学任务也就完成了.但是通过仔细考察这两种方法，可以发现对于泊松问题，两种解法从某种意义上是一致的.

由于在教学前对于Poisson方程的有限差分方法和有限元方法做过一些研究，得到了中心差分格式和P1协调有限元在拟一致的网格剖分下具有相同的H1稳定性和收敛性.故而，在讲完第八章这部分内容后，可以引导学生联系到第五章的内容，让他们寻找两种方法的区别和联系.这样可以加深学生对两种方法的理解，进而得以更好地进行掌握和应用.

事实上，研究者知道所有的数值格式到最后需要求解一个代数方程组.对于有限差分格式系数矩阵为

对于有限元的系数矩阵，通过单刚矩阵合成总刚矩阵，然后进行叠加，有

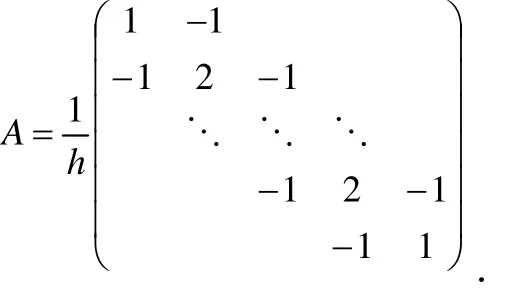
通过这个教学案例，研究者发现把有关教学的科研成果、科研思路和方法，以及自己在科研中获得的新知识和新认识，直接或者间接地传授给学生，不仅可以开拓学生视野、扩大学生知识面，加深学生对本专业、本课程的进一步理解，而且可以增强学生的学习兴趣，发展其创造性思维.

4　教学与科研相结合原则实践的体会

在数学教学过程中，前人已经研究了众多的教育原则[8~11].在这里，研究者结合自身的教学和科研经历，针对偏微分方程数值解这门大学数学课程，对教学与科研相结合这一高等教育原则进行了研究与实践.进而，探讨了利用该原则来培养大学生探求新知识和科学创新的能力.

当前，国家和学校对大学生创新能力的培养尤为重视，各级的“本科教学工程”大学生创新训练计划项目的出现，都支持着大学生这项能力的培养和提高.因此，高校教学必须与科研相结合，才能通过开展基础性的学术活动、实施训练计划和提供相关平台，使学生的科研创新能力得到极大提高，实现高校教育改革的目标.

［参 考 文 献］

[1]李均.高等教育基本原则探析[J].江苏高教，2003，（4）：5-8.

[2]张亚丽.我国高等学校教学原则体系的科学构建[D].兰州大学，2007.

[3]赵婷婷.从大学与社会的矛盾看教学与科研的关系[J].高等教育研究，1999，（2）：47-50.

[4]常晓，魏浩翰.对洪堡思想中“教学与科研相结合”的再思考[J].前沿，2007，（3）：57-59.

[5]钱佩玲.在大学数学教学中应注重贯彻“教学与科研相结合”的原则[J].数学教育学报，1995，4（2）：58-62.

[6]陆金甫，关治.偏微分方程数值解（第2版）[M].北京：清华大学出版社，2004.

[7]刘儒勋，舒其望.计算流体力学的若干新方法[M].北京：科学出版社，2003.

[8]曹月波，吴昭君，田宏根.复变函数教学中直观性原则应用的思考与实践[J].数学教育学报，2011，20（6）：86-88.

[9]张艳霞，龙开奋，张奠宙.数学教学原则研究[J].数学教育学报，2007，16（2）：24-27.

[10]刘耀斌.“归纳与演绎并用”的教学原则[J].数学教育学报，1999，8（4）：26-28.

[11]陈重穆.关于义务教育中的数学教学原则[J].数学教育学报，1995，4（2）：1-9.

[责任编校：周学智]

Practice on Principle of Combining Teaching and Research in Teaching of Numerical Methods of PDEs

HUANG Peng-zhan
(College of Mathematics and System Sciences, Xinjiang University, Xinjiang Urumqi 830046, China)

Abstract:The Combining Teaching and Research is one of the most important principles in higher education. Nowadays, a demand for innovation ability of undergraduate students is made greater importance of this principle. Using it in teaching of Numerical Methods of PDEs, it is found that it can widen teachers’ research vision and broaden their minds, and increase students’learning interest and develop their creative thinking.

Key words:combining teaching and research; numerical methods of PDEs; innovation; principle of higher education

作者简介：黄鹏展（1983—），男，浙江慈溪人，副教授，博士，主要从事偏微分方程数值解的教学与研究.

基金项目：国家自然科学基金——3维定常MHD方程的有限差分有限元解耦迭代方法（11362021）；中国博士后科学基金面上一等资助——不可压缩流动问题的高效二步算法研究（2013M530438）

收稿日期：2015-03-03

中图分类号：G642

文献标识码：A

文章编号：1004-9894（2015）04-0048-03