一种基于小波包变换的电力谐波检测方法
2015-03-11罗冠姗卢惠辉苏成悦何榕礼陈元电
罗冠姗,卢惠辉,苏成悦,何榕礼,陈元电
(1.广州供电局有限公司计量中心,广州市 510730;2.广东工业大学,广州市 510006)
一种基于小波包变换的电力谐波检测方法
罗冠姗1,卢惠辉2,苏成悦2,何榕礼2,陈元电2
(1.广州供电局有限公司计量中心,广州市 510730;2.广东工业大学,广州市 510006)
由于非线性负载用电的不断增加,造成大量谐波返灌电网产生电能污染和计量不公等问题,然而传统的快速傅里叶变换(fast Fourier transform, FFT)检测方法由于自身技术的限制,难以满足目前谐波检测对精确性的要求。结合电力谐波特点,分析小波变换与傅里叶变换原理,提出了一种小波包与FFT相结合并采用加窗双谱线插值的电力谐波检测方法,研究了不同窗函数的特性,并且通过加入不同的窗函数来检测谐波,得出针对电力谐波检测最优的窗函数。仿真实验验证了该方法对谐波在时域和频域上都有很好的测量效果,为谐波电能表电力谐波检测方法及信号截取窗函数选取提供重要参考。
电力谐波;快速傅里叶变换;小波变换;窗函数
0 引 言
随着电力电子装置等非线性负载的广泛应用,大量高次谐波注入电网造成电能质量严重恶化[1-3],严重影响电能计量的准确性和公平性[4]。注入电网的谐波主要以奇数次谐波为主,一般的谐波电能表检测到21次谐波为止,最为普遍的是整流桥产生的(6k±1)次谐波(k为整数)[3]。谐波检测是治理电网谐波问题的关键,目前的谐波检测主要用快速傅里叶变换(fast Fourier transform, FFT)获取各次谐波信号的幅值、频率和相位。但基于FFT的谐波检测方法只适用于稳态谐波检测且计算量大,因而实时性不够好。随着电力谐波的复杂性不断增加,如出现瞬时突变,白噪声干扰等情况,传统的FFT检测精度并不适合检测电力谐波[5-6]。
随着新理论和新技术的进步,谐波检测的方法也有了改进。改进的FFT方法有:采用多峰谱线修正算法[7];利用数字式锁相器使信号频率及采样频率同步减少采样误差[8];采用加入不同窗函数插值算法[9-10]。瞬时无功功率理论常常用于谐波的瞬时检测,也可用于无功补偿等谐波治理领域[11],其依据相关模型(主要有ip-iq和p-q模型等),把电网的有功功率和瞬时无功功率分解为交流部分和直流部分,并将交流部分对应于谐波电流,由此可方便计算出谐波分量。现阶段随着人工神经网络和小波变换理论的应用,为谐波检测研究带来了新的契机[12-14]。小波变换可看做是傅立叶变换的发展,具有傅立叶变换所缺乏的方向选择性、可变的时频域分辨率等特点,因此,可以用在傅立叶变换无法涉足的场合,如对频域和时域同时有局部性要求的检测[15]。神经网络能模仿人脑的部分结构和功能,具有一定的映射能力及自适应、自学习等能力[16]。将神经网络应用于谐波检测,需要搭建合适的映射网络,再确定一个原始样本,选择一种算法训练出一个最优种群,然后将被测的信号数据输入训练好的种群,并得出检测结果。目前神经网络在谐波检测方面的研究尚属起步阶段,实际应用较少。
本文结合传统的FFT和小波包变换理论,使两者优势互补,先对各窗函数特性进行分析,再同时采用加窗双谱线插值形成一种先分析后实践的新方法,通过对比谐波信号检测结果,得出针对电压谐波信号的最优窗函数,实现对电力谐波的高精度检测。
1 谐波检测算法分析
傅立叶变换是以时间为自变量的“信号”函数与以频率为自变量的“频谱”函数之间的某种变换关系,实际工程中有很多信号都无法表示成连续函数解析式,一般时域与频域都采用离散形式,即离散傅里叶变换(discrete Fourier transform,DFT),形式如下:
(1)
式中:k=0,1,2,3…,N-1;N为采样点数;x(n)是第n次采集信号x(t)的采样值。
所以如果计算采样点N的DFT需要进行N2次复数运算,计算量大且耗时长。人们通过利用旋转因子的对称性、周期性和可约性等特性形成FFT[14]。FFT比较简单和方便,但存在频谱栅栏和泄漏等现象影响测量精度[8-9],动态适应能力不如小波变换。对于信号x(t)的连续小波变换[12]为
(2)
式中:wx为积分小波变换;a为伸缩因子;b为平移因子;Ψ*为Ψ的共轭复数;函数Ψ(t)被称为母小波,令其伸缩和平移得到连续的小波基,其表达式为
(3)
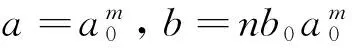
(4)
随着对正交小波基的不断研究,逐渐形成了正交小波包的概念。小波包可以看成是函数空间逐级正交剖分的扩展,能够为信号提供一种更加精细的分析方法[15]。小波包将频带进行多层次划分,对多分辨率分析没有细分的高频部分进一步分解,从而提高了时频分辨率。通过小波包对信号频带的不同层次分解和重构,可以分析信号不同时域的局部变化,从而针对电力谐波信号的低频谐波和高频噪声做出检测和处理,这是傅里叶变换所不能及的。
2 加窗双谱线插值法分析
前面介绍到FFT由于对信号进行一个非整数周期的“加窗”截断,引起频谱泄漏现象。因此,对谐波信号检测需要设计一个合适的窗函数。为降低谐波信号频谱泄漏和兼顾多频率检测分辨率,应适当选择主瓣宽度和旁瓣峰值电平小且衰减速率大的窗函数[10]。图1是hanning、hamming、blackman、nuttall窗函数的特性综合比较。
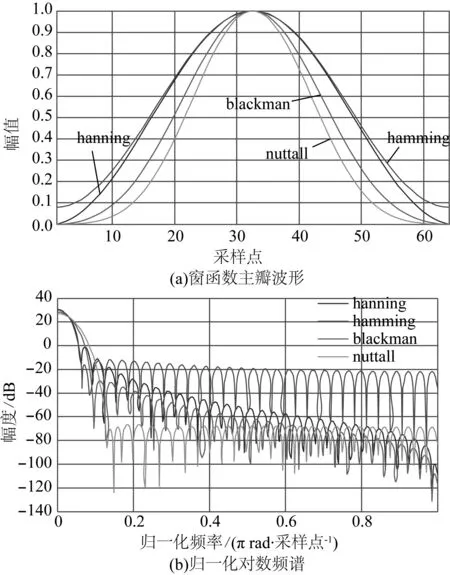
图1 各窗函数特性比较Fig.1 Characteristic comparison of window functions
双谱线插值算法是通过对原始信号加窗FFT后,利用2根谱线的加权平均来修正幅值的双峰谱线,能够较好地克服FFT由于信号频率分量与离散频率点不重合引起的栅栏效应。信号非同步采样时,离散频率间隔为△f=fs/N,N为数据截断长度,得到的离散时间信号为
(5)
式中:A0为信号幅值;f0为信号频率;fs为DSP对信号的采样频率;φ0为信号的初相位。对x(n)加窗函数WR(n),得xW(n)=x(n)WR(n),并转换离散傅里叶变换表达式如下:
(6)
k为离散抽样频率间隔频点,峰值频率f0=k0△f很难处于离散谱线频点上,即k0一般不为整数,设峰值点k0附近幅值最大和次最大的谱线分别为k1和k2,k1≤k0≤k2=k1+1,这2条谱线的幅值分别为y1和y2,N为采样点数,设β=(y2-y1)/(y2+y1),α=k0-k1-0.5,可知α取值范围为[-0.5,0.5],可得
(8)
幅值修正计算公式为
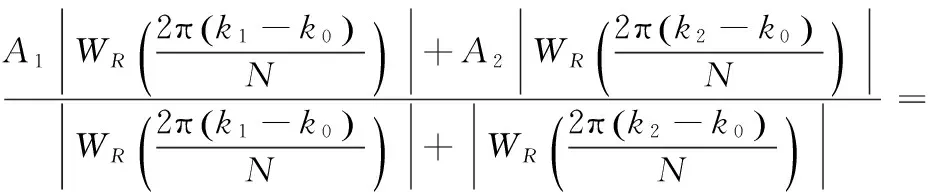
(9)
初相位修正公式为

(10)
3 实验仿真与数据分析
FFT在稳态谐波分析的应用中具有不可替代的作用,但是其分析和处理暂态信号效果较差,因为傅里叶变换不具有时域的分辨率,会把局部信号在整个域里平滑掉。而小波包变换具有良好的时频局部性,能很好反映信号的细节特征,适合反映信号的突发变化和时变跟踪。本实验结合2种方法优势再加上窗函数和双谱线插值法对某公变房谐波电压实测数据进行检测,谐波如表1所示。
表1 某公变房所测电压谐波成分
Table 1 Measured voltage harmonic component in a transformer substation

本实验基于Matlab的平台搭建谐波信号并作出检测和数据分析处理,实验流程如图2所示。为了使仿真更具有实际性,本实验对注入谐波信号添加高频的白噪声,仿真信号如图3所示。
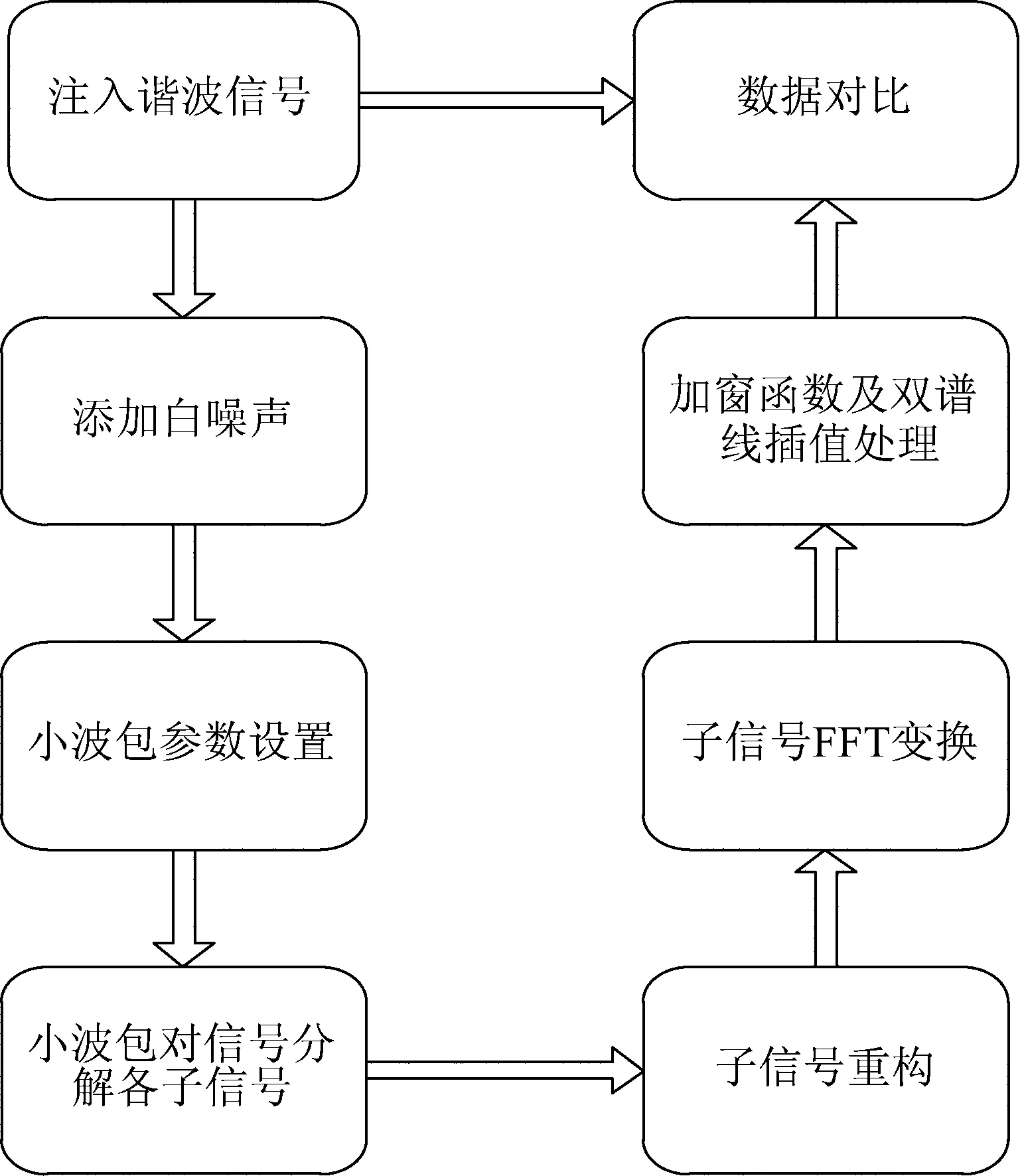
图2 谐波检测流程图Fig.2 Flow chart of harmonic detection

图3 谐波原始信号图Fig.3 Harmonic original signal
利用小波包变换对信号进行处理,首先要针对谐波信号选择合适的小波包函数、采样频率、采样点数、频率的分解层数以及最后一层的频带划分。这里基频为50 Hz, 频带划分的原则是尽量使信号的基频位于最低子频带的中心,为方便提取基波和奇波,频带间隔为0~100 Hz、100~200 Hz、200~300 Hz……。根据谐波的次数来决定分解的层数,这里频率分成5层,则采样频率为6 400 Hz,采样点数为512,即可分辨谐波的最高频率可以达到3 200 Hz,采用db44小波包函数,图4为信号分解树形图。但是信号子空间频带的频率大小并非按照分解树节点编号的大小顺序排列,各个结点重构信号的频率范围不易判定,本文通过分析小波包变换的Mallat分解算法与分解滤波器的关系,对分解的各子信号重新排序重构,波形如图5所示(S0代表原始信号,S1代表0~100 Hz信号,S3代表100~200 Hz……)。
图4 信号频率分解5层的小波树Fig.4 5 layers of wavelet signal frequency decomposition tree
由图5可知,小波包变换具有良好的时域局部化特性,可以有效适用于分析电力信号任意时刻某频段谐波的场合。但由于频带划分的界限效应导致其频域分辨率相比FFT较弱,要测试电力信号具体的频率成份需要对子信号进行FFT,如图6所示。一般实验通过小波包变换与子信号的FFT变换,就可得出各次谐波的频谱情况和幅值,但是针对一些各次谐波幅值相差大或存在噪声的信号,只采用该方法所得出的谐波幅值和相位的误差大,因此本实验还采取对各子信号采取加窗双谱线插值法改善对信号的采样和处理,图7为各窗函数对信号检测结果。
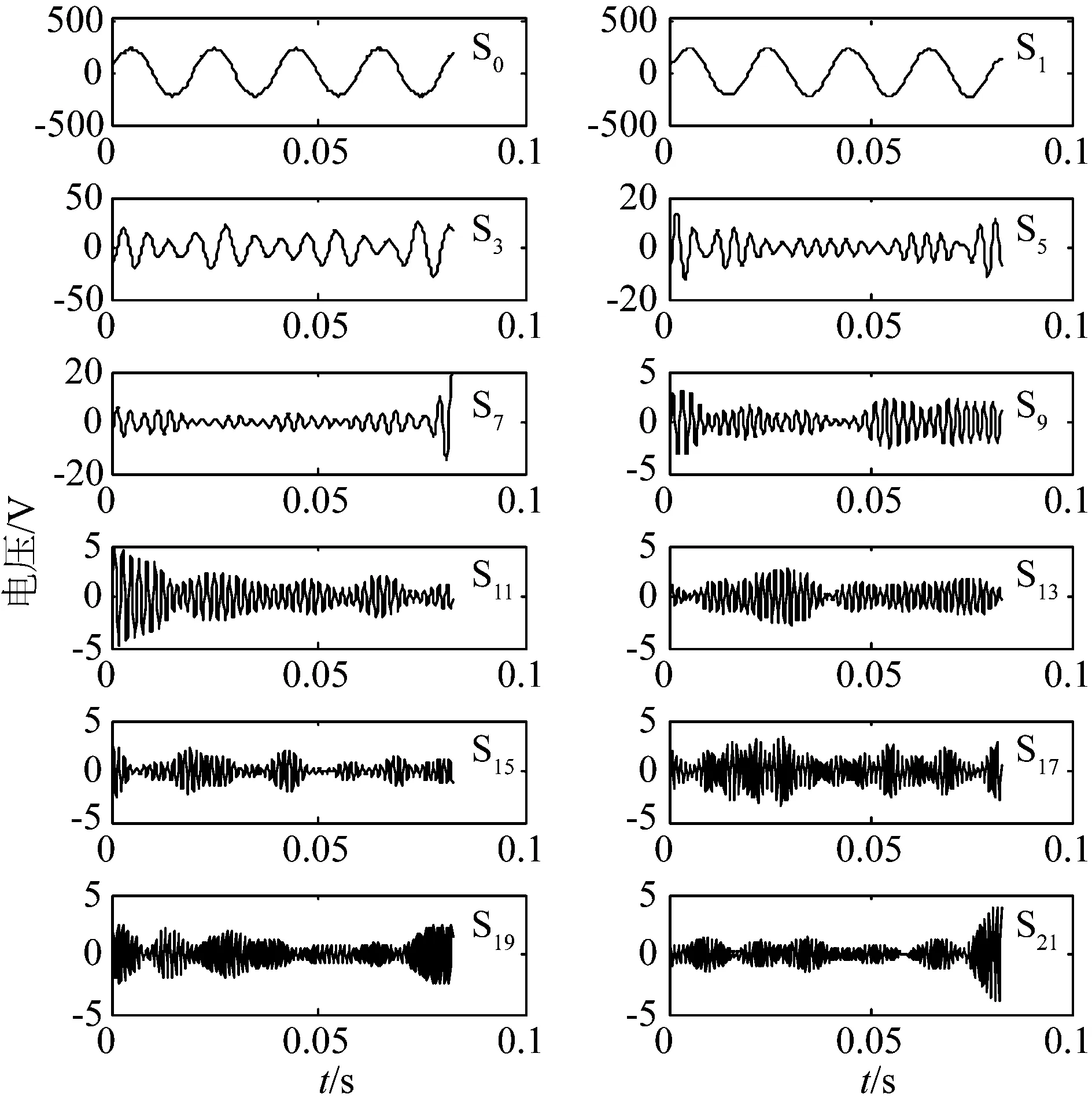
图5 小波包重构各子信号时域波形Fig.5 Wavelet packet reconstruction of each signal time domain waveform

图6 各次谐波信号FFT变换Fig.6 FFT of harmonic signal
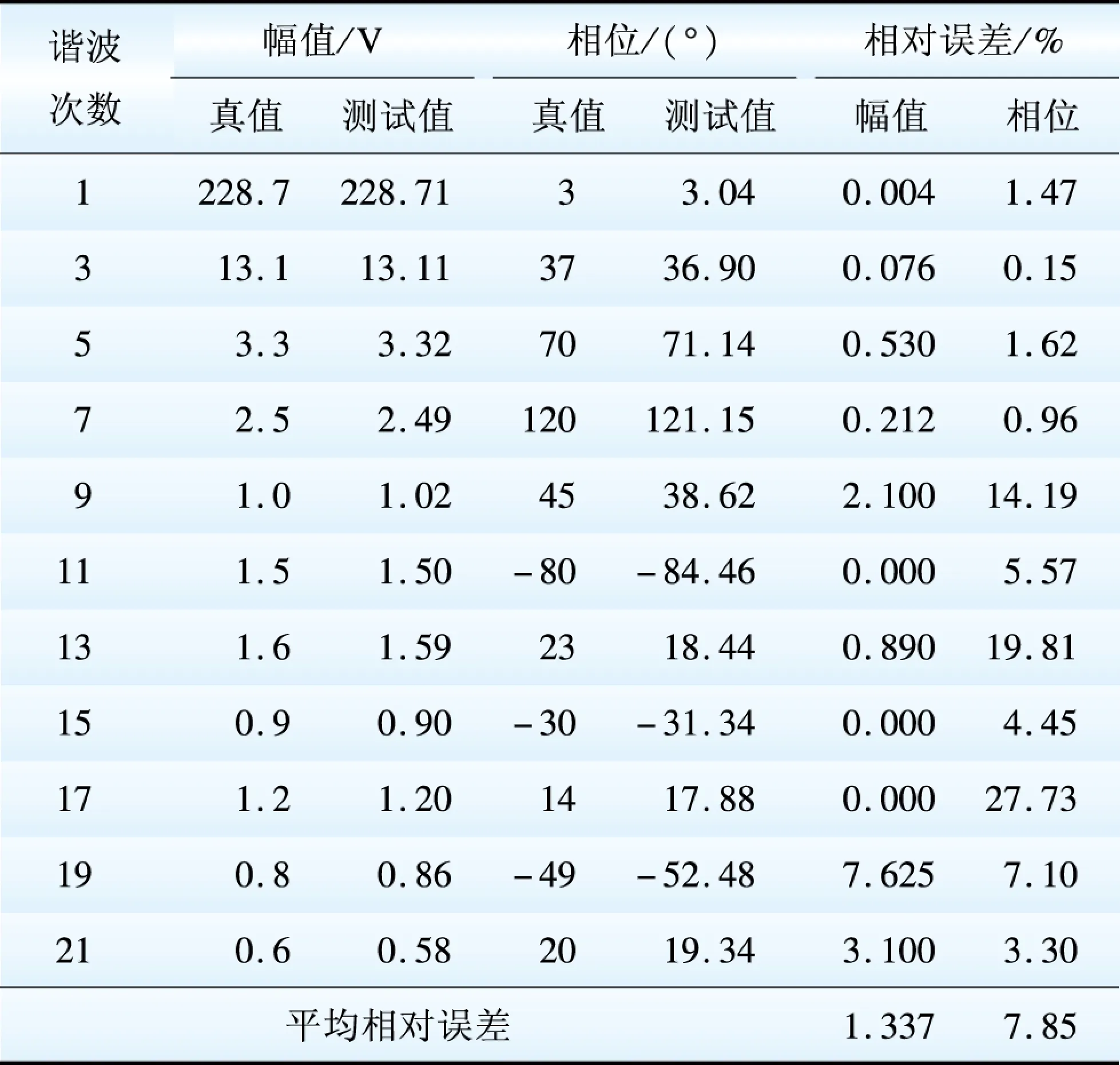
图8为各窗函数检测信号结果相对误差,由图8可知,插入各个窗函数的结果差距较为明显,其中通过加入hanning窗函数用双谱线插值法检测的信号结果与原信号谐波真值最为接近,各次谐波相对误差最小,而nuttall窗函数对该谐波信号检测较差,两者的幅值平均相对误差相差17%,检测精度相差1个数量级。结合图1各窗函数的特性分析,造成差异的主要原因是hanning窗的主瓣宽度较大,能量集中在主瓣内,且旁瓣衰减速率大(约18 dB/oct)可以有效抑制长范围频谱泄漏,而nuttall窗函数虽然旁瓣峰值很低,有效抑制短范围泄漏,但衰减率低只有6 dB/oct,不适宜谐波幅值落差大的信号。hanning窗具体数据如表2所示,其中相位的平均相对误差为7.85%,幅值检测效果很好,平均相对误差为1.337%,最大的相对误差为7.625%,各谐波检测误差的变化与双谱线插值的同步采样问题以及噪声的影响有关,尤其是高次谐波低幅值的信号更容易受噪声的影响。

图7 各窗函数检测信号结果Fig.7 Signal detection results by each window function
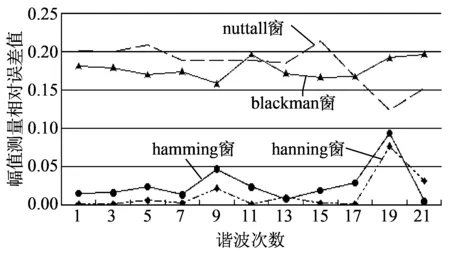
图8 各窗函数检测信号结果相对误差对比Fig.8 Results relative error by each window function表2 信号测试结果Table 2 Signal test data results
4 结 论
本文仿真结果体现出对谐波分析小波包变换具有良好的时频局部化特性,就像一个显微镜可以观察到信号的各次谐波细节,克服了传统傅立叶变换时域无局部化特性。同时利用FFT高度的频域分辨率和加窗函数双谱线插值法实现对各次谐波的幅值和相位的提取。经过加入不同的窗函数的效果对比,发现加入hanning窗函数的结果最为理想,所测幅值的平均误差为为1.337%,而nuttall窗函数的效果较差,表明针对各次谐波幅值落差较大的电力谐波信号检测,选取主瓣宽度和旁瓣衰减率合适的窗函数至关重要,为电力系统谐波检测提供了重要的参考。
[1]姚猛,蒋德珑,陈根永.基于模糊聚类的电网谐波综合评估方法[J].电测与仪表,2011,48(10):1-4,24.Yao Meng, Jiang Delong, Chen Genyong.Application of fuzzy clustering on power grid harmonic comprehensive Evaluation[J].Electrical Measurement & Instrumentation, 2011,48(10):1-4,24.
[2]蒋平,罗曦,顾伟,等.谐波分析及谐振评估软件的开发与应用[J].电力自动化设备,2009,29(4):126-130.Jiang Ping, Luo Xi, Gu Wei, et al.Development and application of harmonic resonance analysis and assessment software[J].Electric Power Automation Equipment,2009,29(4):126-130.
[3]肖湘宁.电能质量分析与控制[M].北京:中国电力出版社,2010:195-200.
[4]郭继芳,冯力鸿.谐波对电能计量表影响的分析[J].电气时代,2010,(3):85-88.
[5]房国志,杨超,赵洪.基于FFT和小波包变换的电力系统谐波检测方法[J].电力系统保护与控制,2012,40(5):75-79.Fang Guozhi, Yang Chao, Zhao Hong.Detection of harmonic in power system based on FFT and wavelet packet[J].Power System Protection and Control, 2012, 40(5):75-79.
[6]亓学广.基于FFT和小波变换的电力系统谐波检测方法研究[D].青岛:山东科技大学,2007.Qi Xueguang.Study on harmonic detection methods in power system based on FFT and wavelet transform[D].Qingdao: Shandong University of Science and Technology, 2007.
[7]黄冬梅,龚仁喜,焦凤昌,等.莱夫-文森特窗三谱线插值的电力谐波分析[J].电力系统保护与控制,2014,42(2):28-34.Huang Dongmei, Gong Renxi, Jiao Fengchang, et al.Power harmonic analysis based on Rife-Vincent window and triple-spectral-line interpolation[J].Power System Protection and Control, 2014,42(2):28-34.
[8]殷庆平,牛晓平.电力系统谐波测量中频谱泄漏问题的研究[J].工矿自动化,2007(4):28-30.Yin Qingping, Niu Xiaoping.Research of the problem of spectrum leakage in harmonics measurement of power system[J].Industry and Automation, 2007(4):28-30.
[9]卿柏元,滕召胜,高云鹏,等.基于Nuttall窗双谱线插值FFT的电力谐波分析方法[J] .中国电机工程学报,2008,28(25):153-158.Qing Baiyuan, Teng Zhaosheng, GaoYunpeng, et al.An approach for electrical harmonic analysis based on Nuttall window double-spectrum-line interpolation FFT[J].Proceedings of the CSEE, 2008, 28(25):153-158.
[10]Zolfaghari R; Shrivastava Y, Agelidis V G.A comparison between different windows in spectral and cross spectral analysis techniques with Kalman filtering for estimating power quality indices[J].Electric Power Systems Research,2012, 1(84):128-134.
[11]陈文杰,万钧力,黄悦华.基于瞬时无功功率理论的三相电路谐波和无功电流检测[J].机电信息,2013(3):140-142.
[12]冯新民.小波包变换在电网谐波检测中的应用研究[J].机械工程与自动化,2011(4): 160 -162.Feng Xinmin.Application of Wavelet Package Transform in Power Grid Harmonic Detection[J].Mechanical Engineering & Automation,2011(4):160-162.
[13]谢东,张兴,曹仁贤.基于小波变换与神经网络的孤岛检测技术[J] .中国电机工程学报,2014,34(4):537-544.Xie Dong, Zhang Xing, Cao Renxian.Islanding detection based on wavelet transform and neural network[J].Preceedings of the CSEE, 2011,34(4): 537-544.
[14]张汉中,肖继学,杨琳,等.傅里叶与小波变换的电力谐波测试性能研究[J].中国测试,2014,40(2):135-140.Zhang Hanzhong, Xiao Jixue, Yang Lin, et al.Research on test performance of power harmonic for methods of Fourier transform and wavelet transform[J].China Measurement & Test, 2014,40(2):135-140.
[15]黄文清,戴瑜兴,全慧敏.基于Daubechies小波的谐波分析算法[J].电工技术学报,2006,21(6):45-50.Huang Wenqing, Dai Yuxing, QuanHuimin.Harmonic estimation method based on Daubechieswavelet[J].Transactions of China Electrotechnical Society, 2006,21(6):45-48.
[16]岳明道,郭焕银,李文艺.一种基于神经网络的电力谐波检测方法[J].仪表技术,2012(12):1-4.Yue Mingdao, Guo Huanyin, Li Wenyi.Power harmonic detection method based on neural network[J].Instrumentation Technology, 2010(12):1-4.
(编辑:张小飞)
An Detection Method for Power Harmonic Based on Wavelet Packet Transform
LUO Guanshan1, LU Huihui2, SU Chengyue2, HE Rongli2, CHEN Yuandian2
(1.Measuring Center of Guangzhou Power Supply Bureau Co., Ltd., Guangzhou 510730, China;2.Guangdong University of Technology, Guangzhou 510006, China)
As the nonlinear load increases, a large number of harmonic will back to fill the grid which may result in the power pollution and measuring inequality.However, the traditional fast Fourier transform (FFT) detection methods are difficult to meet the harmonic detection requirements for accuracy due to the limitation of their own technology.Combined with the characteristics of power harmonic form, this paper analyzed the principle of wavelet transform and Fourier transform, and put forward a kind method with double-spectrum-line and window function based on the wavelet packet combined with FFT.This paper mainly studied the characteristics of different window functions, and added them to get the optimal window function for power harmonic detection by comparison.The simulation results verify that the harmonic measurement method has a good measurement effect in time domain and frequency domain, and the simulation experiment provides a good reference for the detection method of power harmonic of harmonic watt-hour meter and the selection of window function of signal interception.
power harmonic; fast Fourier transform (FFT); wavelet transform; window function
TM 935
A
1000-7229(2015)03-0071-06
10.3969/j.issn.1000-7229.2015.03.012
2014-10-25
2014-12-25
罗冠姗(1972),女,工程师,主要从事电能计量管理、电力营销管理等工作;
卢惠辉(1988),男,硕士,主要研究方向为电力电子;
苏成悦(1961),男,博士,教授,主要研究方向为应用物理;
何榕礼(1974),男,硕士,讲师,主要研究方向为应用电子;
陈元电(1977),男,硕士,讲师,主要研究方向为无线电与移动通信。
