基于EMD与ELM的输电线路山火蔓延速度组合预测模型
2015-03-11李晋伟王奇何红太裴冠荣
李晋伟,王奇,何红太,裴冠荣
(1.南方电网超高压输电公司检修试验中心,广州市 510663;2.北京国网富达科技发展有限责任公司,北京市 100070)
基于EMD与ELM的输电线路山火蔓延速度组合预测模型
李晋伟1,王奇1,何红太2,裴冠荣2
(1.南方电网超高压输电公司检修试验中心,广州市 510663;2.北京国网富达科技发展有限责任公司,北京市 100070)
针对复杂环境下输电线路山火的影响因素,提出了基于经验模态分解(empirical mode decomposition,EMD)与极端学习机(extreme learning machine,ELM)的输电线路山火预测模型。首先利用小波去噪对采集的风速时间序列进行噪声分析,根据序列的不同进行归类重构,产生新的风速时间序列;然后利用经验模态分解将输电线路山火成因分解为一系列具有不同特征尺度的子序列;接着利用交叉验证法和重构相空间法确定学习机的各种参数和输入维数;再利用极端学习机输电线路山火进行建模预测分析。仿真结果表明基于经验模态分解与极端学习机的输电线路山火组合预测模型可以有效预测24 h之内的山火蔓延速度,为实现输电线路山火在线较高精度的预测提供了可能。
山火;经验模态分解(EMD);多分辨率分析;极端学习机(ELM)
0 引 言
近年来,随着电力资源的开发,越来越多的输电线路穿过高山峻岭地带,这些地区独特的地形地貌、气候条件极易引发山火,轻则引起输电线路跳闸,重则造成烧毁铁塔,引起长时间的不可恢复的重大电力事故。山火是造成输电线路跳闸的主要因素之一,随着电网规模的不断扩大,加之近年极端干旱天气的频繁出现,山火已成为危害电网安全稳定运行的重要因素之一。据不完全统计数据[1-6]表明,山火对我国输电线路造成极大威胁。如2001年至2008年南方电网输电线路因山火引起的线路跳闸共37次;2010年至2012年,云南电网110 kV 及以上输电线路因山火引起的线路跳闸共25次,尤其是2012年3月30日500 kV宝七Ⅰ、Ⅱ回线跳闸,已构成了三级电力安全事件。
广西电网110 kV及以上电压等级输电线路累计发生山火跳闸31起,此外,有20余次输电线路受山火影响而被迫紧急停运。国外如南非、巴西、美国以及澳大利亚都发生过因山火引发线路跳闸的事故。燃烧的山火正逼近电网,为积极应对严峻的山火形势,国内外相关学者对山火引发线路跳闸的机理、山火监测及预警、山火引发线路故障模型等进行了深入的研究。国内武汉大学吴田[5-6]等研究了500 kV输电线路山火击穿特性及跳闸机理,文献[7]研究了山火条件下的架空输电线路停运概率模型,给出了输电线路停运概率与山火距离、浓烟浓度、温度、湿度等关系。国外也有很多学者对输电线路在山火条件下的闪络特性进行了大量研究[8-10]。文献[11]利用HJ卫星遥感对澳大利亚东南部森林山火进行监测,能够反映出火灾的局部空间分布和细节特征。文献[12]研究了极轨气象卫星在输电线路防山火监测中的应用。但基于卫星的监测系统存在实时性差、漏报和误报、对范围很小的山火在数据处理方面不易识别等缺点,给准确识别山火带来一定的困难。文献[13]利用卫星遥感和视频图像等传感器实现了架空输电线路走廊防山火综合监测系统,这也同样存在实时性差、漏报和误报、烟雾传感器灵敏度受现场微气象(风向)环境影响的问题。
本文在以上研究成果的基础上,针对复杂环境下输电线路山火的影响因素,提出了基于经验模态分解与极端学习机的输电线路山火预测模型。首先利用小波对采集的风速信号进行小波去噪;然后利用经验模态分解将输电线路山火成因风速分解为一系列具有不同特征尺度的子序列;接着利用极端学习机对输电线路山火蔓延速度进行建模预测分析;最后给出仿真结果。
1 山火数学模型
根据输电线路空气间隙的平均温度与山火形成的火场状,可以预测与点火源不同距离的输电线路发生故障的概率,根据文献[9]所述,点火源起火后,当无风时,形成一个圆形火场,其火蔓延速度方程为
(1)
式中:v0为山火蔓延速度,km/h;Ir为反应强度;ξ为热通量比系数;ρb、ε、Qig均为可燃物特性相关的常数。然而若受风速的影响,火焰将沿各个方向以不同速度蔓延,就会形成一个以点火源为焦点的椭圆形火场。椭圆的长轴方向为最大火蔓延速度方向,与风矢量方向一致。最大火蔓延速度[14]为
v=v0(1+ψv)
(2)
式中ψv为风速修正系数。
定义k为椭圆的半长轴a与短半轴b的比值,即k=a/b,用来表征椭圆的形状,其经验公式为k=1+λV。λ为系数,参考值为0.25s/m;V为风速,km/h。
根据火蔓延速度和可燃物条件,一般利用美国Byram的公式[15]估计火线强度。根据火线强度,可以根据经验公式[16]计算火线区域温度。
因此,由公式(1)、(2)可知,只要知道了风速就可以利用相关的公式计算得出山火蔓延速度。然而,风速具有很强的非线性和随机性特性,并且在采集风速信息时不可避免地存在噪声的干扰,所以利用传统的方法预测山火的蔓延速度存在较大的误差。
2 理论描述
2.1 经验模态分解
经验模态分解是一种基于信号局部特征的信号分解方法,适用于非线性非平稳信号分析,是一种自适应的信号分解方法。经验模态分解方法假设:任何复杂的信号都是由简单的固有模态函数(intrinsicmodefunction,IMF)组成,且每一个IMF都是相互独立的[17]。EMD分解的具体步骤为:
(1)根据序列x(t)的所有极大值点和所有极小值点利用样条插值分别获得上包络信号x1(t)和下包络信号x2(t),并计算上包络和下包络信号的平均值:
(3)
(2)计算x(t)与m(t)的差值h(t),将h(t)作为新的x(t),重复以上操作,直到h(t)满足IMF条件时,记c1(t)=h(t),则c1(t)为第1个IMF分量,它包含了原始序列中的最短周期分量。
(3)从x(t)中减去分离出来的第1个IMF信号c1(t),得到余差信号r(t),即
r(t)=x(t)-c1(t)
(4)

(5)
该方法可以将风速数据时间序列中真实存在的不同尺度或趋势分量逐级分解出来,产生一系列具有相同特征尺度的数据序列,分解后的序列与风速原始数据序列相比具有更强的规律性,可以提高预测精度。然而,分解出来的各个序列必然存在测量噪声,因此,还需要对各个序列进行去噪,考虑到序列的非线性和随机性,本文采用小波去噪。
2.2 小波去噪

VJ=VJ-1⊕WJ-1=VJ-2⊕WJ-2⊕WJ-1=…
(6)
对任意信号x(t)∈L2(R),都可以用分辨率分解为
(7)
式中:J为分解的层数;c0(k)为尺度系数;dj(k)为小波系数,若尺度函数是一组正交基,则cj(k)、dj(k)可分别表示为
(8)
由双尺度方程可知:
(9)
式中:h(k)、g(k)分别为低通滤波器系数和高通滤波器系数,且满足:
g(k)=(-1)kh(1-k)
(10)
初始的尺度系数cj(k)可由信号x(t)直接采样获得。如果信号的采样频率大于Nyquist频率,那么cj(k)就可以很好地逼近信号x(t),也就是说,在该尺度下我们不需要小波系数dj(k)。
由以上分析和推导,我们得到了信号分解的各频率成分的小波系数,可以把它们表示成矩阵的形式,如式(11)所示:
Csignal=[c0,d0,d1,…,dJ-1]
(11)
式中J为分解层数。
根据测量噪声的特点,设置各个小波系数的阈值,高于设定阈值的部分保留,低于设定阈值的部分置为0,获得重构用的小波系数,即
(12)
将式(12)代入重构方程得到:
(13)
即可滤除原始信号中的噪声。
2.3 极端学习机

οk=ωTf(Winxk+b),k=1,2,…,N
(14)
式中:xk为输入向量;Win为连接输入节点和隐层节点的输入权值;b为隐含层偏置;ok为网络输出;ω为连接隐含层与输出层的输出权值;f为隐含层激活函数,一般趣味Sigmoid函数,N为样本数。
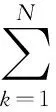
ωTf(Winxk+b)=tk,k=1,2,…,N
(15)
将式(15)写成矩阵形式为Hω=T,其中:

极端学习机克服了传统神经网络训练速度慢、容易陷入局部最小等缺点。特殊的学习机理可有效克服传统神经网络基于梯度学习算法的缺陷,采用简单的线性回归即可得到令人满意的解。
3 山火组合预测模型
(1)由相关理论可知,风速时间序列具有明显的非线性和非平稳性,同时小波去噪具有较好的处理非平稳数据能力,本文采用小波去噪对风速时间序列进行去噪,获得信噪比较高的风速时间序列。
(2)由于EMD 分解具有较好的处理非线性数据的能力,采用EMD 分解对风速时间序列进行分解,以产生一系列的不同尺度的固有模态信号IMF和剩余分量r。
(3)对上述得到的各子时间序列分别建立ELM预测模型进行预测,最后将各子序列的预测结果进行叠加即可得到风速预测值。具体预测流程见图1所示。

图1 基于 EMD 和ELM 组合预测流程Fig.1 Combined prediction flowchart based on EMD and ELM
(4)利用风速预测值和风速与山火蔓延速度之间的数学关系即可获得山火组合预测模型。
4 仿真实验
为了验证本文所提方法的正确性,利用采集的720组间隔1 h的风速,采用Matlab进行了仿真分析。696组数据作为训练数据,剩余的24组数据作为验证数据,验证24 h内的山火蔓延速度。原始风速时间序列如图2所示。
利用小波去噪算法对上述的风速时间序列进行去噪,得到如图3所示的重构风速时间序列。
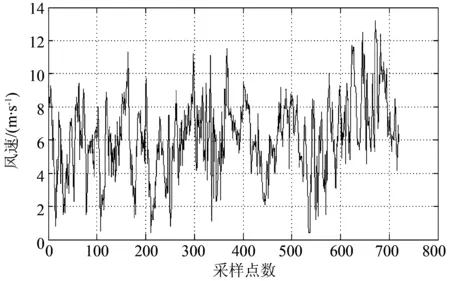
图2 风速时间序列Fig.2 Time series of wind speed
采用的小波去噪阈值系数如表1所示。
风速时间序列经过小波分解后采用EMD对其进行分解,得到各个风速子序列(IMF)如图4所示。
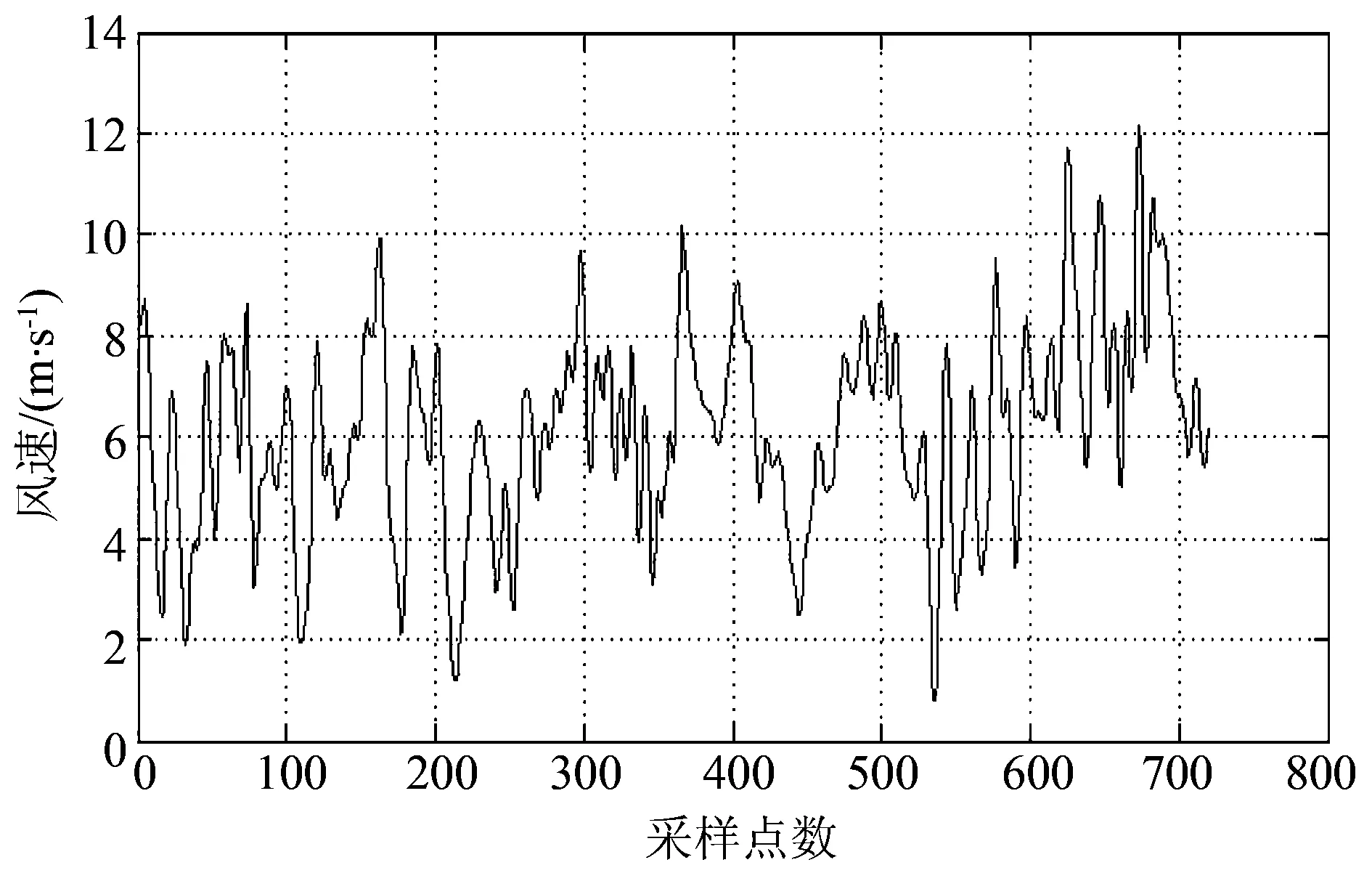
图3 去噪后的风速时间序列Fig.3 Time series of wind speed after de-noising表1 小波去噪阈值系数Table 1 Threshold coefficients of wavelet de-noising

针对EMD处理得到的各个风速子序列利用ELM进行预测,并进行叠加得到风速预测值,利用公式(2)和风速预测值得到山火蔓延速度组合预测结果如图5所示。
由图5可知,本文所提山火组合预测模型与山火蔓延速度模型一致,验证了本文所提方法的正确性。

图4 经EMD处理后的风速子序列Fig.4 Wind speed subsequences processed by EMD
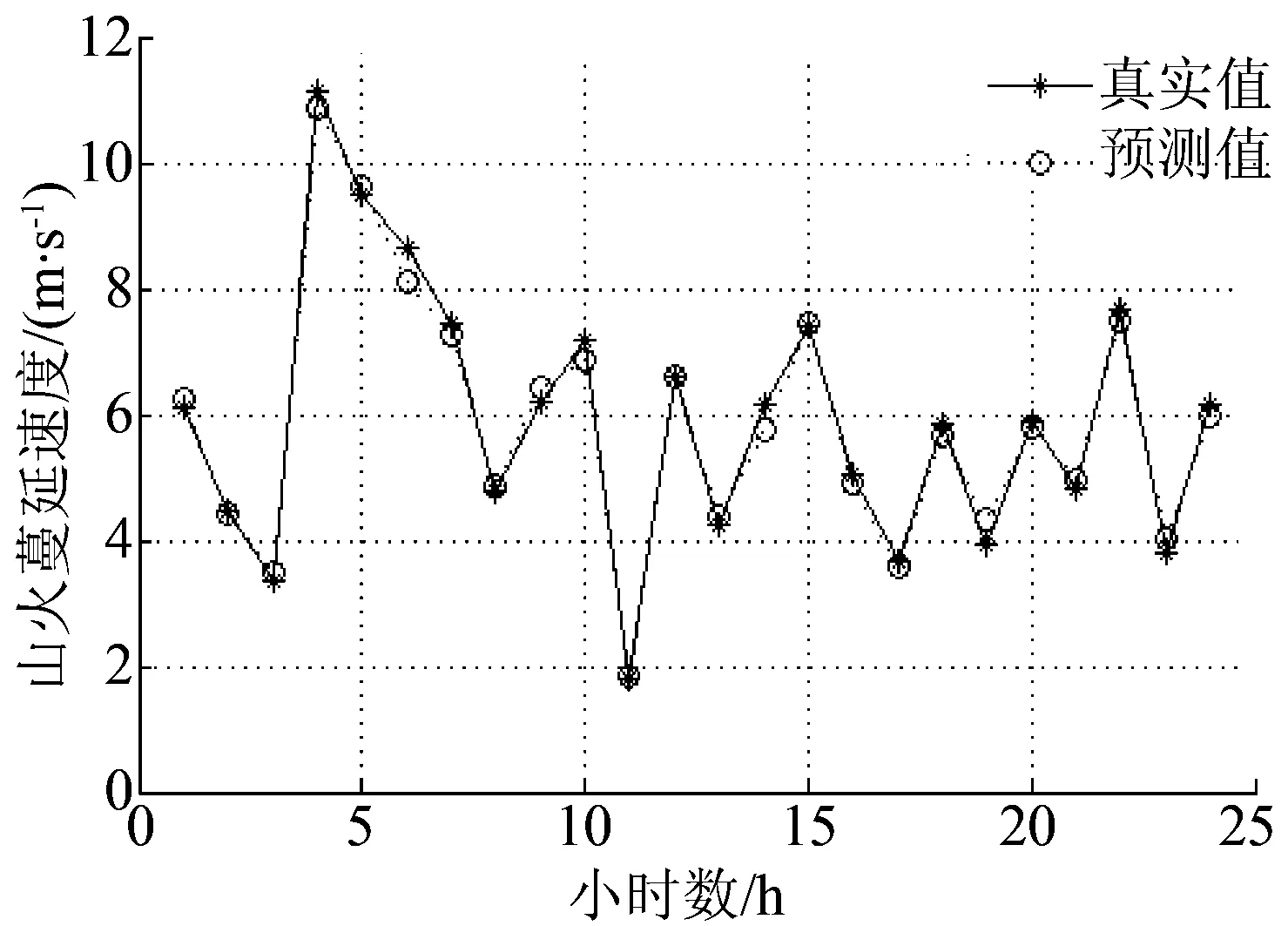
图5 山火蔓延速度24 h预测结果Fig.5 Predict results of fire spread speed within 24 h
5 结 论
(1)该方法首先利用小波对采集的风速时间序列进行去噪;然后利用经验模态分解将输电线路山火成因风速分解为一系列具有不同特征尺度的子序列;最后利用极端学习机对输电线路山火蔓延速度建立了组合预测模型。
(2)利用该模型可以有效预测24 h内的山火蔓延速度情况,为相关电力部门保障输电线路运行而采取的措施提供了基础,可以降低山火引起的输电线路停运概率。
[1]廖旎焕, 胡智宏, 马莹莹, 等.电力系统短期负荷预测方法综述[J].电力系统保护与控制, 2011, 39(1): 47-52.Liao Nihuan, Hu Zhihong, Ma Yingying, et al.Review of the short-term load forecasting methods of electric power system[J].Power System Protection and Control, 2011, 39(1): 47-52.
[2]黄乐, 舒双燕.南方电网2010 年第一季度线路山火跳闸情况分析[J].广东电力, 2011, 24(3): 95-97.Huang Le, Shu Shuangyan.Analysis on fault trips caused by forest fire in CSG in the first quarter of year 2010[J].Guangdong Electric Power, 2011, 24(3): 95-97.
[3]宋国兵, 蔡新雷, 高淑萍, 等.高压直流输电线路故障定位研究综述[J].电力系统保护与控制, 2012, 40(5): 133-137.Song Guobing, Cai Xinlei, Gao Shuping, et al.Survey of fault location research for HVDC transmission lines[J].Power System Protection and Control, 2012, 40(5): 133-137.
[4]李勇, 陶雄俊, 陈立.输电线路山火故障分析及预防[J].湖北电力, 2010, 34(6): 49-50.Li Yong, Tao Xiongjun, Chen Li.The analysis and precautions of forest fire fault to transmission line[J].Hubei Electric Power, 2010, 34(6): 49-50.
[5]吴田, 胡毅, 阮江军, 等.交流输电线路模型在山火条件下的击穿机理[J].高电压技术, 2011, 37(5): 1115-1122.Wu Tian, Hu Yi, Ruan Jiangjun, et al.Air gap breakdown mechanism of model AC transmission line under forest fires[J].High Voltage Engineering, 2011, 37(5): 1115-1122.
[6]吴田, 阮江军, 胡毅, 等.500 kV 输电线路的山火击穿特性及机制研究[J].中国电机工程学报, 2011, 31(34): 163-170.Wu Tian, Ruan Jiangjun, Hu Yi, et al.Study on forest fire induced breakdown of 500 kV transmission line in terms of characteristics and mechanism[J].Proceedings of the CSEE,2011,31(34):163-170.
[7]宋嘉婧,郭创新,张金江,等.山火条件下的架空输电线路停运概率模型[J].电网技术,2013,37(1):100-105.Song Jiajing, Guo Chuangxin, Zhang Jinjiang, et al.A probabilistic model of overhead transmission line outage due to forest fire[J].Power System Technology, 2013, 37(1): 100-105.
[8]Mphale K, Heron M, Ketlhwaafetse R, et al.Interferometry measurement of ionization in a grassfire[J].Meteorology and Atmospheric Physics, 2010, 106(2-3): 191-203.
[9]Naidoo P, Swift D A.Large particle initiated breakdown of an atmospheric air gap: relating to AC power line faults caused by sugar cane fires [C]//The 8th International Symposium on High Voltage, Engineering.Yokohama, 1993.
[10]Kim I.Flashover characteristics of vertical-type model power line in the presence of combustion flash[J].Journal of the Korean Institute of Illuminating and Electrical Installation Engineer, 2009, 23(5): 58-65.
[11]李家国,顾行发,余涛.澳大利亚东南部森林山火HJ卫星遥感监测[J].北京航空航天大学学报, 2010, 36(10): 1221-1224.Li Jiaguo, Gu Xingfa, Yu Tao.Detection of Australian southeast forest fire using HJ satellite[J].Journal of Beijing University of Aeronautics and Astronautics, 2010,36(10):1221-1224.
[12]梁允,李哲,曲燕燕,等.极轨气象卫星在输电线路防山火监测中的应用[J].河南科学,2013,31(10): 1664-1667.Liang Yun, Li Zhe, Qu Yanyan, et al.The polar orbit meteorological satellite and its application in monitoring mountain fire for transmission line[J].Henan Science,2013,31(10):1664-1667.
[13]雷国伟,何伟明,林健枝.架空输电线路走廊防山火综合监测系统实现与应用[J].电气技术,2013(12):112-115.
[14]王海晖,朱霁平,姜伟,等.森林地表火行为估算的数学模型[J].火灾科学,1994,3(1):33-41.Wang Haihui, Zhu Jiping, Jiang Wei, et al.A mathematical model for estimating surface fire behavior[J].Fire Safety Science, 1994,3(1):33-41.
[15]Byram G M.Combustion of forest fuels[M].New York,USA:McGraw Hil,1959:61-89.
[16]张景忠,肖非,廉明起.林火行为相关参数综合测报仪的研究[J].东北林业大学学报,2000,28(6):112-115.Zhang Jingzhong, Xiao Fei, Lian Mingqi.The comprehensive measuring instrument of parameters relating to forest fire behavior[J].Journal of Northeast Forestry University,2000,28(6):112-115.
[17]Huang N E,Shen Z,Long S R, et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society London A,1998(454):903-995.
[18]袁琦,周卫东,李淑芳,等.基于ELM 和近似熵的脑电信号检测方法[J].仪器仪表学报,2012,33(3):514-519.Yuan Qi, Zhou Weidong, Li Shufang, et al.Approach of EEG detection based on ELM and approximate entropy[J].Chinese Journal of Scientific Instrument,2012,33(3):514-519.
[19]Huang G B, Zhu Q Y, Siew C K.Extreme learning machine: theory and application[J].Neurocomputing, 2006, 70(1-3): 489-501.
(编辑:张媛媛)
Mountain Fire Spread Speed Combined Forecasting Model for Transmission Line Based on EMD and ELM
LI Jinwei1, WANG Qi1, HE Hongtai2, PEI Guanrong2
(1.Maintenance & Test Centre, CSG EHV Power Transmission Company, Guangzhou 510663, China;2.Beijing Guowang Fuda Science&Technology Development Co., Ltd., Beijing 100070, China)
According to the impact of mountain fire of transmission line in complex environment, the mountain fire prediction model was proposed based on the methods of empirical mode decomposition (EMD) and extreme learning machine (ELM).Firstly, the noise of collected wind speed time series was analyzed by using wavelet transform, and the classification and reconstruction were carried out according to the different sequences, in order to reconstruct new wind speed time series.Secondly, the factors of the mountain fire were decomposed into a series of sub-sequences with different characteristics scales by using EMD.Thirdly, cross-validation method and phase space reconstruction method were used to determine various parameters and input dimensions of machine learning, and then the modeling and forecasting analysis was carried out for the mountain fire of transmission line by using ELM.The simulation results show that the combined forecasting model for the mountain fire of transmission lines based on EMD and ELM can effectively predict fire spread speed within 24 h, which can provide the possibility to realize the online prediction of the mountain fire in transmission line with high precision.
mountain fire; empirical mode decomposition(EMD); multi-resolution analysis; extreme learning machine(ELM)
国家高技术研究发展计划项目(863计划)(2012AA050209)。
TM 75
A
1000-7229(2015)03-0027-06
10.3969/j.issn.1000-7229.2015.03.005
2014-09-22
2014-10-15
李晋伟(1986),男,工学硕士,工程师,主要从事超高压输变电设备在线监测、故障测距、电力系统参数辨识及风险评估研究工作;
王奇(1983),男,博士,高级工程师,主要从事电力系统稳定与控制、直流及串补控制保护方面工作;
何红太(1975),男,高级工程师,主要从事输变电设备在线监测研究工作;
裴冠荣(1981),女,工学硕士,工程师,主要从事输变电设备在线监测研究工作。
The National High Technology Research and Development of China(863 Program)(2012AA050209)。
