主成分分析法在河流水质评价中的应用

张海平 郝彩侠 郝敏霞 马立山 马冬梅

(1.河北建筑工程学院,河北 张家口 075000；2.石家庄市冶河灌区引岗管理处,河北 石家庄 050000)

主成分分析法在河流水质评价中的应用

张海平1郝彩侠1郝敏霞2马立山1马冬梅1

(1.河北建筑工程学院,河北 张家口 075000；2.石家庄市冶河灌区引岗管理处,河北 石家庄 050000)

河流水质的污染物种类多且具有不同程度的相关性，在不损失初始水质数据所包含信息的前提下，利用主成分方法对某河流市内河段8个断面的氨氮、溶解氧、总磷等7项水质数据进行分析，从结果中提取数量较少且不具有统计相关性的主成分变量2个，第一主成分中高锰酸钾指数、总磷、总氮有相对较高荷载，第二主成分中溶解氧、硝酸盐氮有相对较高荷载，累计方差贡献率约92%且第一主成分远大于第二主成分，进而分析该河水质的主要影响污染物类型及其所占比重，并通过主成分综合评价函数对各断面水质综合污染情况排名，结论表明主成分方法的评价结果与实际情况相符合，并达到降维、简化数据和提高分析结果可靠性等目的.

河流；水质；污染物；评价；主成分分析

1 原 理

对河流进行水质评价是水环境质量评价的主要内容之一，目前我国的大多数河流已经受到了不同程度的污染，通过河流水质评价可以为河流水资源合理开发利用以及水体污染综合防治提供依据.

水质评价常用的数学方法主要包括简单指数法、综合污染指数法、分级加权平均法、模糊数学法、普通概率统计法等等，每种评价方法有不同的理论基础，在实际评价中对结论侧重不同，具有不同的应用价值[1].

由于河流污染物种类和来源的多样性，使水质评价过程中需要考虑的污染物因子很多，这些因子经常来自于同一个总体，其中有些是主要因子，有些是次要因子[2]，每个污染物因子本身在反映水质一方面状况的同时，各因子之间又呈现不同程度的相关性，使水质内容构成了一个多因子的复杂系统[3].在水质评价中需要监测的污染物项目很多，评价结果也受多个因子影响，导致评价计算量和分析问题复杂性的增加，使一些评价方法在进行水质评价时表现出一些不足之处，所以进行定量分析的评价过程中，我们希望涉及的变量较少而得到的信息量较多，主成分分析是解决这一问题的理想工具.

主成分分析(Principal Component Analysis，PCA)，也称为主分量分析方法，是多元统计分析的一个分支，是一种常规的综合评价统计方法.在多因子变量评价过程中，每个因子除了本身包含的信息之外，因子之间也具有统计相关性，因此一些统计方法计算得到的结果所反映的信息在内容上有重叠.主成分方法是基于降维思想，把多个原始因子转化为较少的几个综合因子，原理是统计学中的方差法，通过提取原始变量的信息形成一组新的综合变量，综合变量的方差越大，表明该变量所包含的原始信息越多，评价中贡献率越高，影响也较强.新构成的综合变量在统计中称为主成分，每个主成分都是原始变量的线性组合，由于主成分之间不具有统计相关性，避免了主成分各单项包含信息的重叠.主成分分析法不需要专家打分，相比较层次分析法及模糊综合评价等更具有数据处理的客观性.

在水质评价中，通过主成分法可以简化分析结构，在不损失初始水质数据所包含信息的前提下，将常规的较多种类的水质污染物因子重新组合成一组彼此之间在统计上不相关的、数量有所减少的综合因子，达到降维、简化数据和提高分析结果可靠性等目的.

主成分分析方法在水污染的评价中主要有两种应用方式，一种是通过对一组观测点数据的分析，建立一个综合评价指标，然后根据该指标对采样点的污染程度进行评级；另外一种方式是通过评价各污染物在综合指标中的贡献率，区分造成污染的主要和次要污染物[4].

2 研究背景

研究选取位于北方某河流的市内河段作为对象，该河全长109公里，流域总面积2380平方公里，是一条多泥沙的季节性河流.为了改善河流水质及两岸环境，对市区总长7780米的河道进行治理，合计共建设16座橡胶坝，形成连续近10公里，约102万平方米的水面，总蓄水量将达到281万立方米，成为集防洪排涝、景观蓄水、休闲娱乐为一体的典型城市水体.

选取市区评价河段的8个断面作为水质评价的样本点、根据河道的水质特点和监测情况，选取市区各断面氨氮(NH3-N)、硝酸盐氮(NO3-N)、高锰酸盐指数(KMnO4)、五日生化需氧量(BOD5)、溶解氧(DO)、总磷(TP)、总氮(TN)等7项污染物作为研究对象(表1).其中溶解氧DO在水质反映上与其他污染物相反，DO值越大表示水质越好，其他污染物则是随着数值的增大，水质越差.为了使数据具有一致性，对溶解氧数据做简单预处理，取溶解氧的实测数据与饱和溶解氧(取10 mg/L)之差[5].

本研究采用了社会科学统计软件SPSS(Statistical Program for Social Sciences)进行计算，SPSS是在很多研究领域和行业被广泛应用的统计学分析软件，具有理论基础严谨、功能内容丰富的特点.

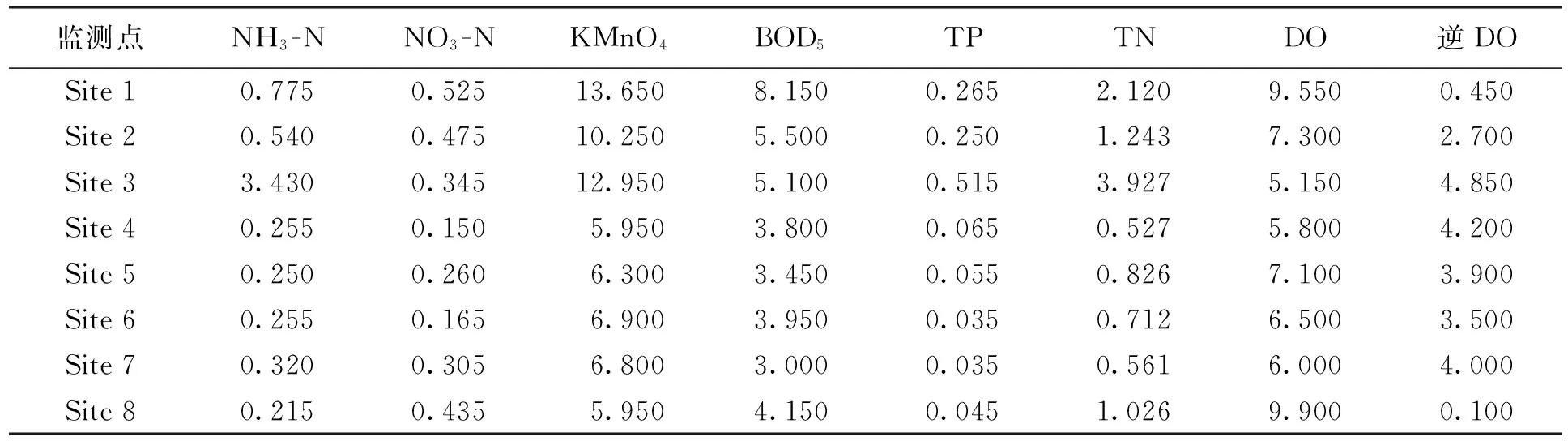
表1 2013年各监测点污染物数值

3 应 用

主成分分析的主要步骤包括了几个步骤：(1)标准化；(2)相关性分析；(3)确定主成分个数、表达式；(4)评价综合主成分分值[6-9].

3.1 监测数据的标准化

在进行分析前，为了消除各监测数据原始量纲和数量级不相同的影响，要对原始变量矩阵进行标准化的处理，方法是对同一变量减去其均值再除以标准差.

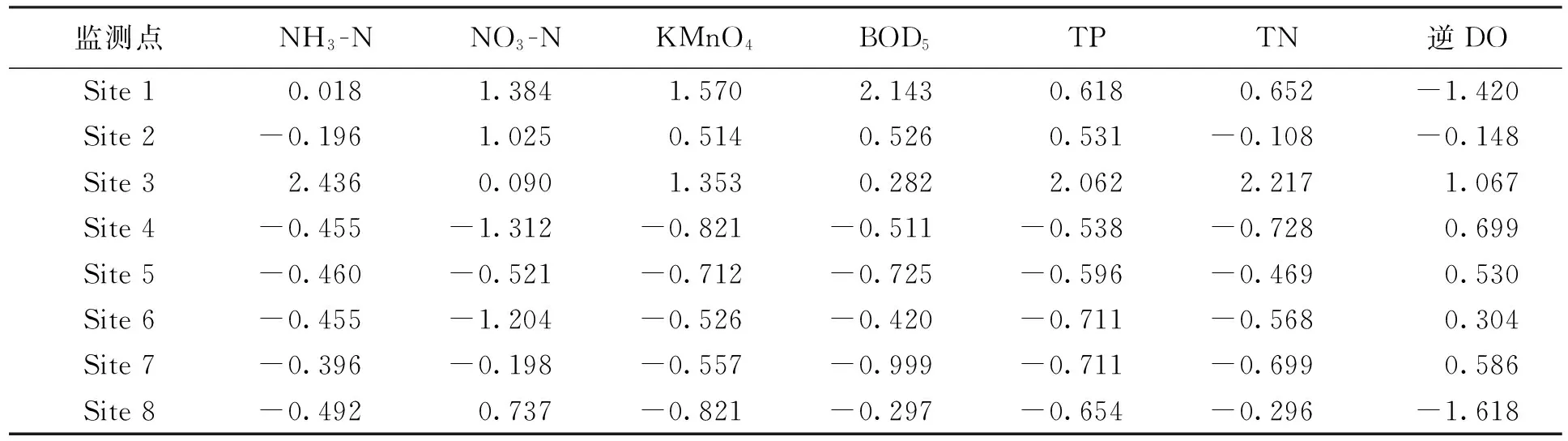
表2 标准化处理后的数据

3.2 相关性分析

计算求得各水质污染物间的相关系数，列入表3相关系数矩阵.

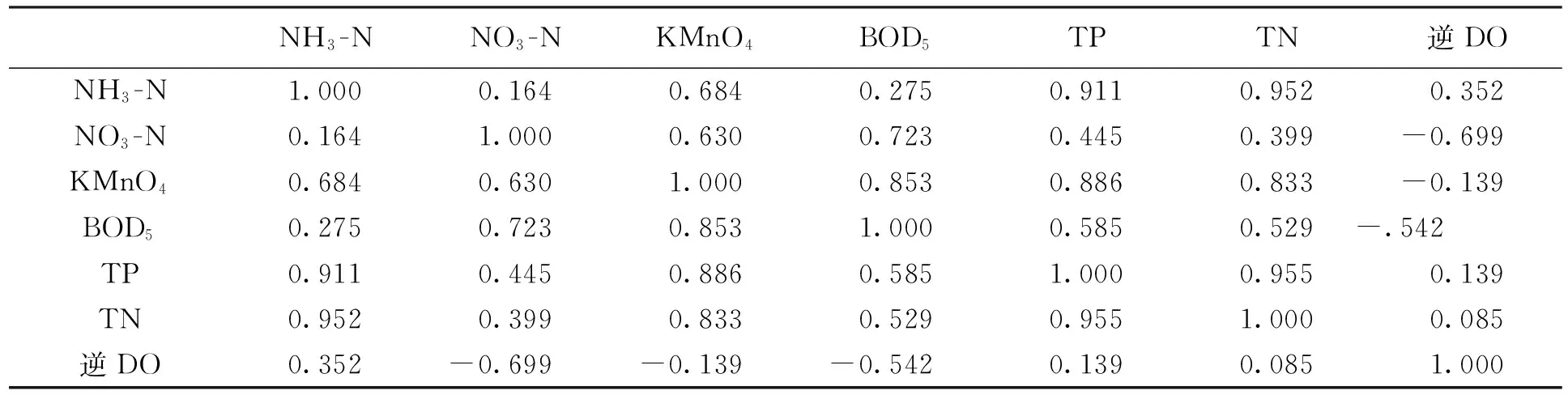
表3 各水质污染物相关系数矩阵

从水质的相关系数矩阵中可以看到，多数污染物之间相关系数是比较大的，例如氨氮和总磷的相关系数0.911，高锰酸盐指数和总氮的相关系数0.833，即这些变量的相关性较强，说明这些变量包含的水质信息有重叠，较适合主成分分析方法.

3.3 确定主成分个数、表达式、命名

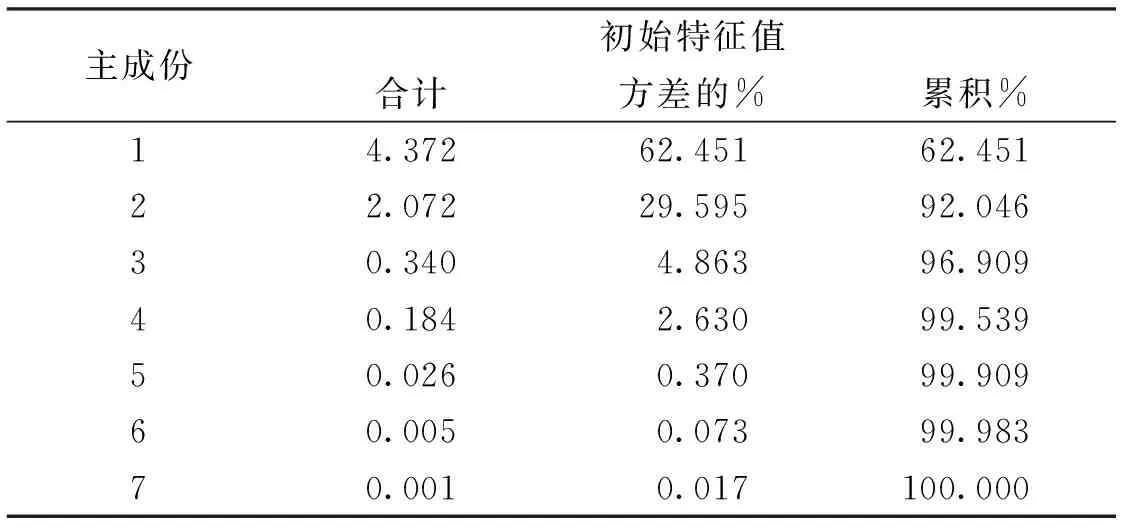
表4 水质污染物特征值和主成分贡献率及累计贡献率

计算水质污染物的特征值和主成分贡献率及累计贡献率，列入表4中，然后根据初始特征值的方差累计贡献率进一步定出主成分的个数.

主成分是以最少的个数反映尽量多的信息为原则，确定主成分个数时有一些判断标准，如选取特征根大于1且发生数值突变的成分，累计百分比达80%-85%等[10]，根据以上标准考察表4内容，可以得出本组数据的主成分个数为2，此时累计方差贡献率已达到92.046%，大于85%，说明这2个主成分反映了原始变量提供的92%的信息.

确定主成分后，计算这两项主成分的初始因子载荷矩阵，并进一步计算主成分载荷矩阵，主成分载荷矩阵是用初始因子载荷矩阵中的数据除以主成分相对应特征值的平方根，主成分载荷矩阵表示了两个主成分中每个污染物所对应的系数，数据见表5.

表5 主成分载荷矩阵

从表4的主成分贡献率可以看出，第一主成分的方差贡献率是62.451%，远大于第二主成分20.595%的方差贡献率，说明在本组监测数据中的河流中污染物主要体现在第一主成分中.主成分载荷矩阵体现了各污染物与主成分之间的紧密度，污染物与某一主成分的荷载系数的绝对值越大，则该主成分与污染物之间的联系越紧密，从表5的主成分荷载中可以到，对于第一主成分，高锰酸钾指数、总磷、总氮有相对较高的荷载，对于第二主成分荷载，溶解氧、硝酸盐氮有相对较高的荷载，即第二主成分主要反映的是这两个污染物的信息.所以，从主成分贡献率及荷载情况可以看出该河水质的主要影响污染物类型及其所占比重[11,12].

3.4 评价综合主成分分值.

根据表5中各污染物主成分荷载系数，可以确定主成分表达式，以及综合评价函数，如下:

根据综合评价函数，计算各监测点水质污染的主成分评价方法的综合得分值，结果列入表6，得分和排名反映了水质污染程度的综合化定量描述，得分越高，表明污染越严重.

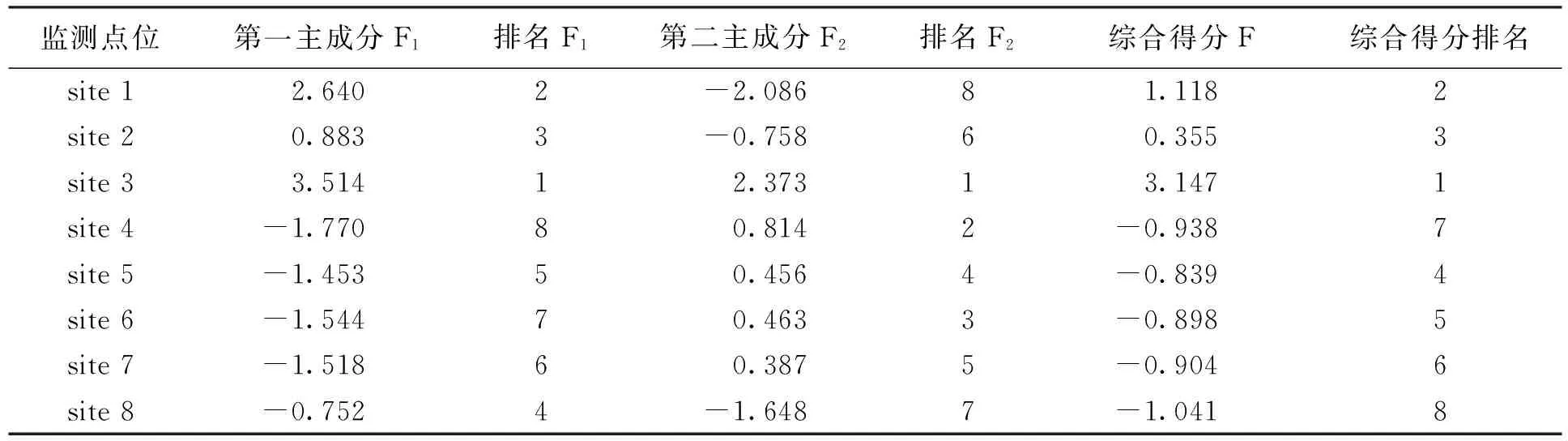
表6 断面水质的主成分得分及排序

从表中结论可以看出，该河段水质污染程度各断面综合排序为：3>1>2>5>6>7>4>8，单独从主成分F1得分的排名来看，3号和1号监测点得分远高于其他监测点，说明该两点水质污染物以高锰酸钾指数、总磷、总氮为主；以第二主成分F2排名来看，3号监测点同样得分远高于其他监测点，说明此处溶解氧、硝酸盐氮污染较重.从水质监测数据中也可以看出3号点各项污染物浓度多数高于其他监测点，可见主成分分析方法是可以真实地反映了实际情况的.

4 结 论

通过对该河段多个监测点水质数据的分析，可以看出利用主成分分析的方法可以充分的表现出全部数据所包含的信息，通过主成分的各污染物贡献率来考量污染物的重要性，通过主成分得分来比较监测点污染程度，分析过程不需要专家咨询，具有基于数据的客观性和全面性，能够全面的反映水质污染的综合水平，可以为水环境质量的研究提供评价工作.但是该方法并不难完全取代定量分析的工作，而且由于所有结论都是基于检测数据得出的，所以在应用上受到数据统计等方面的影响.

[1]姬志宏，姬志新，许正彪，等.主成分分析法在黄河三门峡库区水质评价中的应用[J].华北水利水电学院学报，2012，33(1)：126～130

[2]李娜.基于主成分分析法的延河水质评价及预测[J].人民珠江，2014，3:105～108

[3]伊元荣，海米提·依米提，王涛，等.主成分分析法在城市河流水质评价中的应用[J].干旱区研究，2008，25(4)：497～501

[4]郭翔云，崔慧敏.主成分分析法在白洋淀水质评价中的应用[J].海河水利，2005，5:55～56

[5]盛周君，孙世群，王京城，等.基于主成分分析的河流水环境质量评价研究[J].环境科学与管理2007，32(12)：172～175

[6]刘路，高品，陈刚，等.城市河流各水期水质变化分析[J].中国环境监测，2012，28(2)：115～118

[7]王艾，冯绍元，郑艳.主成分分析法在温榆河水质评价中的初步应用[J].北京水务，2011，2：49～52

[8]鲁斐，李磊.主成分分析法在辽河水质评价中的应用[J].水利科技与经济，2009，12(10):660～662

[9]方红卫，孙世群，朱雨龙，等.主成分分析法在水质评价中的应用及分析[J].环境科学与管理，2009，34(12):152～154

[10]吉祝美，方里，张俊，等.主成分分析法在SPSS软件中的操作及在河流水质评价中的应用[J].环境研究与监测，2012，25(4)：68～73

[11]杨竞，童祯恭，刘玉哲.SPSS软件对饮用水水质进行主成分分析评价的运用[J].环境科学与技术，2011，34(7):171～174

[12]秦天玲，候佑泽，郝彩莲，等.基于主成分分析法的武烈河流域水质评价研究[J].环境保护科学，2011，37(6)：102～105

On the Application of Principal Component Analysis in River Water Quality Evaluation

ZHANGHai-ping1,HAOCai-xia1,HAOMin-xia2,MALi-shan1,MADong-mei1

(1.Hebei Institute of Architectural and Civil Engineering,Zhangjiakou 075000,China;
2.Shijiazhuang Ye River irrigated area Yingang administrative office,Shijiazhuang 050000,China)

The river water pollution is a serious problem,so a simple and accurate evaluation method is needed for better understanding of the pollution factors.In this paper,principal component analysis is used.Along a urban river,8 monitoring sites are selected,7 pollution factors including NH3-N,NO3-N,KMnO4,BOD5,DO,TP,TN are analyzed,and two principal components are selected to reflect the overall pollution factors.As a result,an equation is established to make a comprehensive evaluation of the chosen principal components,the result of which is compared with the original data.The conclusion shows that PCA is a reliable method for water pollution evaluation.

river;water quality;pollutant;evaluation;principal component analysis

2014-10-23

河北省高等学校自然科学青年基金项目(2011239)

张海平(1977-)，男，讲师，从事水资源利用与保护研究.

TV 21

A