含释放时间的单机模糊调度问题

李 凯， 张 勋， 孙秋景， 王明星

（1.合肥工业大学 管理学院，安徽 合肥 230009；2.合肥工业大学 过程优化与智能决策教育部重点实验室，安徽 合肥 230009）

传统的确定型生产调度问题假定作业的加工时间、释放时间、交货期等参数是确定的实数，因此可以根据问题的复杂性确定合理的优化方法，进而得到最优或近优的调度方案。然而，调度中的时间参数因受制造原材料、机器运行状况、工人的熟练程度和环境变化等不确定因素的影响使其具有模糊不确定性，从而促进了人们对模糊调度问题的研究。

图1所示为一个典型拉动式供应链的运作过程。设t1为客户下订单时间；t2、t3分别为制造商订购原材料时间和供应商供应原材料所需时间；t4为作业加工时间；t5为客户取货时间。在拉动式供应链中，客户订单驱动生产，因此运作过程为客户下订单，制造商向供应商订购原材料并组织生产，进而组织配送。以作业释放时间为例，其取值由t1、t2、t3组成。可见影响释放时间的因素不仅复杂，并且均来自制造型企业外部，参数取值难以控制。因此，精确预测作业释放时间并确定其取值将非常困难，难以实现。本文结合上述背景，对该类含有释放时间的单机模糊调度问题展开研究，探讨这些问题解的特点和求解方法。

图1 拉动式供应链结构

近年来，模糊调度受到普遍的关注，其中最常见的是假设作业加工时间是模糊的，文献［1－2］研究了模糊加工时间的单机调度问题；文献［3－4］研究了模糊加工时间的平行机调度问题；文献［5］研究了模糊加工时间的流水作业调度问题；文献［6－8］研究了模糊加工时间的车间作业调度问题；文献［9－11］研究了模糊交货期的调度问题。上述文献通常不考虑作业的释放时间对调度的影响，默认各作业在加工的过程中都是紧邻的，即作业之间无时间空隙，则作业的完工时间可以通过模糊数的加法进行计算。

本文认为模糊释放时间的调度问题在现实生产生活中更加普遍存在，其原因是释放时间不仅与客户相关，也受到原材料供应商以及生产环境的影响，因此更加难以提前确定其取值。然而，关于模糊释放时间调度问题的研究成果较少。若考虑作业的释放时间，必定涉及当前作业释放时间与前驱作业完工时间的比较，此时仅采取模糊数的加法运算将无能为力。本文将作业的释放时间假设为区间模糊数，并定义区间模糊数之间的max运算，进而实现对模糊释放时间调度问题的求解。

图2 区间模糊数max运算示意图

在研究模糊释放时间调度问题的过程中，采用了与现有模糊调度文献不同的研究思路。①调度方案的选取。现有模糊调度文献通常只给出某一调度方案，并认为该方案是最优或较优的。由于模糊调度问题中存在着不确定性，并且现实中不同的决策者对模糊性有着不同的态度，因此模糊调度问题不再是确定的优化问题，而应该是一个决策问题。本文为乐观和悲观2种类型决策者构造了不同的调度方法。②调度方案的评价。一个决策问题的解决过程大致可分为预测、优化或决策方案的制定、优化或决策方案的实施以及事后评价这4个阶段。预测与优化或决策方案的制定属于事前行为，可能存在模糊性；对于一个具体问题的优化或决策方案，事后评价时应基于该具体问题发生时的确定数据。然而，现有模糊调度文献通常将调度方案对应的模糊数转化为某一实数，进而通过实数间的比较来实现模糊调度方案的优劣评价，因此仍属于事前评价。本文认为模糊性存在于事前并且会给不同偏好决策者的决策方案质量产生扰动，因此将采用事后评价的方法对不同决策方案的最终质量进行评价。

本文研究模糊单机调度问题，调度的目标是最大完工时间最小化，其中假定作业具有不同的释放时间且释放时间或加工时间为区间模糊数。

1 区间模糊数的定义和比较

1.1 区间模糊数的描述

定义1 称A＝［，］＝｛x｜≤x≤，∈R｝为区间模糊数和称为A的下限和上限。特殊地，当＝时A为一确切的实数。

定义2 区间模糊数A＝［，］和B＝］，称A＋B＝］＋［，］＝［＋，＋］为A和B的模糊和。显然，对于实数b，A＋b＝］＋［b，b］＝＋b＋b］。

定义3 区间模糊数A＝］和B＝［，］，称max（A，B）＝max（B，A）＝［max，），max）］为区间模糊数的max运算。特殊地，一个区间模糊数A＝］和一个实数b间的max运算定义为 max（A，b）＝max（b，A）＝［max，b），max（，b）］。

图2所示为3种不同情形下2个区间模糊数A＝］与B＝］的max运算结果。

举例说明考虑与不考虑模糊释放时间时对应调度问题的区别，同时也说明在考虑释放时间为区间模糊数的调度问题中区间模糊数max运算的必要性。

设在单机制造系统中有2个作业J1和J2需要加工，且加工次序为（J1，J2），即J1在J2之前加工，所需加工时间分别为p1＝［2，5］、p2＝［3，4］。考虑2种情形：① 作业J1与J2同时释放，记其释放时间分别为r1＝r2＝0；② 作业J1与J2不同时释放，其释放时间分别为r1＝［2，3］、r2＝［3，9］。则2种情形下对应作业最大完工时间Cmax，即作业J2的完工时间C2，计算方式如下：

第1种情形由于作业同时释放，因此Cmax＝C2＝p1＋p2＝［2，5］＋［3，4］＝［5，9］。

第2种情形由于作业J1的开始时间（记为S1）必定在其释放时间之后，可令S1＝r1＝［2，3］，从而J1的完工时间C1＝S1＋p1＝［2，3］＋［2，5］＝［4，8］。作业J2的开始时间（记为S2）必须在作业J2的释放时间之后，同时也要保证作业J1已完工，因此S2＝max（r2，C1）＝max（［3，9］，［4，8］）＝［4，9］，从而可以计算出Cmax＝C2＝S2＋p2＝［4，9］＋［3，4］＝［7，13］。

1.2 区间模糊数的比较操作

事前信息模糊性的存在使得确定的优化问题转变为决策问题，此时具有不同偏好的决策者在制定决策方案时对信息的模糊性必然持不同的态度。结合本文研究的最小化最大完工时间的单机模糊调度问题，如下准则反映出乐观决策者和悲观决策者在模糊决策问题中的不同偏好。

由于研究的调度问题目标为最小化形式，在上述4个准则中，乐观决策者在决策时主要依据信息所代表的乐观情况（此处为区间模糊数的下限），因此首先依据乐观准则1进行决策，乐观准则2为其候补决策准则。以此类推，悲观决策首先依据悲观准则1进行决策，悲观准则2为其候补决策准则。由于乐观决策者与悲观决策者关注于模糊数的不同方面，因此可能导致双方对同一模糊数认识的不一致。由以上准则给出定义。

定义4 当且仅当乐观准则得到A≥B且悲观准则同时得到A≥B，才认为A与B是可比的，此时A≥B。

定义5 当且仅当乐观准则得到A≤B且悲观准则同时得到A≤B，才认为A与B是可比的，此时A≤B。

定义6 当乐观准则得到A≥（≤）B而悲观准则得到A≤（≥）B，则A和B是不可比的，记为A≠B。

由以上定义不难得出：

2 问题描述

问题假设如下：设有n个作业组成作业集合J＝｛J1，J2，…，Jn｝，其中Jj（j＝1，2，…，n）表示第j个作业。所有作业均由同一机器加工。对于任意作业Jj（j＝1，2，…，n），记其释放时间为rj、加工时间为pj。作业加工不允许中断并且机器不能同时加工多个作业。作业Jj（j＝1，2，…，n）的开始时间和完工时间分别记为Sj和Cj。设π＝（Jπ（1）Jπ（2）…Jπ（n））为任一调度方案，其中Jπ（j）（j＝1，2，…，n）表示序列π第j个加工的作业。Sπ（1）≥rπ（1），Cπ（1）＝Sπ（1）＋pπ（1）；对 2≤ ∀j≤n，Sπ（j）≥max（Cπ（j－1），rπ（j）），Cπ（j）＝Sπ（j）＋pπ（j）。调度的目标是寻找最优的调度序列π使得作业的最大完工时间Cmax＝Cπ（n）在所有调度方案中最小。

根据作业释放时间与加工时间模糊性，结合调度问题的三参数表示法，本文涉及4类问题。

P1：1｜rj｜Cmax问题，即释放时间和加工时间均为实数。

P2：1｜rj，Fuzzy（pj）｜Cmax问题，即释放时间为实数，加工时间是模糊数。

P3：1｜Fuzzy（rj）｜Cmax问题，即释放时间是模糊数，加工时间为实数。

P4：1｜Fuzzy（rj），Fuzzy（pj）｜Cmax问题，即释放时间与加工时间均为模糊数。

显然，问题P1、P2、P3是问题P4的特殊情形；问题P1又是问题P2、P3的特殊情形。这里，假定模糊的参数为区间模糊数，即，。

对于经典的确定型调度问题P1，给定任意的作业加工序列π＝（Jπ（1）Jπ（2）…Jπ（n）），其最大完工时间 Cmax＝Cπ（n）＝ max｛Cπ（n－1），rπ（n）｝＋pπ（n）＝｝，并且知道作业按照释放时间小者优先（Earliest Release Date firstly，ERD）排序能够得到问题P1的最优解。

定理1 对于作业加工时间为区间模糊数的问题P2，任意调度序列π＝（Jπ（1）Jπ（2）…Jπ（n）），作业Jπ（j）（1≤π（j）≤n）的完工时间，。

证明 归纳法。

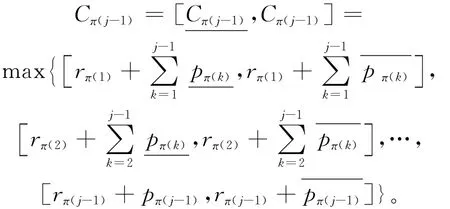
则

从而，问题P2的最大完工时间为：

由定理1，可以得到推论1、推论2。

推论1 对于作业释放时间为区间模糊数的问题P3，任意调度序列π＝（Jπ（1）Jπ（2）…Jπ（n））对应的最大完工时间为：

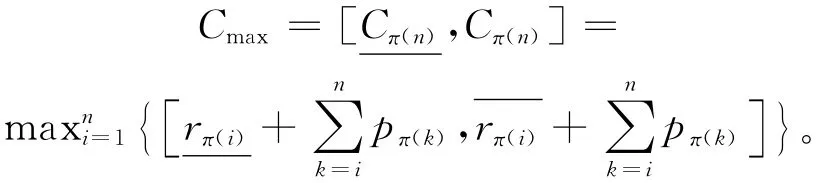
推论2 对于作业释放时间与加工时间均为区间模糊数的问题P4，任意调度序列为π＝（Jπ（1）Jπ（2）…Jπ（n））对应的最大完工时间为：

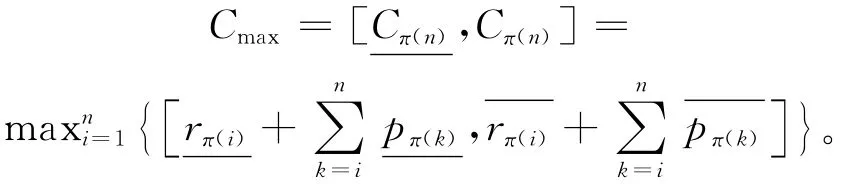
3 问题求解

问题P1是问题P2～P4的特殊情形，且该类经典确定型调度问题可以通过ERD规则获得最优解。对于问题P2，定理2证明了ERD规则对该类问题同样有效。

定理2 对于问题P2，作业的ERD序列仍为最优解。

证明 反证法。

假设最优调度规则S得到的序列π＝（Jπ（1）Jπ（2）…Jπ（j）Jπ（j＋1）…Jπ（n）），设作业Jπ（j）在时间T 开始加工，紧接着加工Jπ（j＋1）Jπ（j＋2）…Jπ（n），其中rπ（j）＞rπ（j＋1），交换作业Jπ（j）和Jπ（j＋1）的位置得到调度S′，此时得到的序列为π′＝（Jπ（1）Jπ（2）…Jπ（j＋1）Jπ（j）…Jπ（n）），作业Jπ（j＋1）的开始加工时间为T，紧接着加工Jπ（j）Jπ（j＋2）…Jπ（n）。

在调度规则S下π的前j＋1个作业的完工时间为：

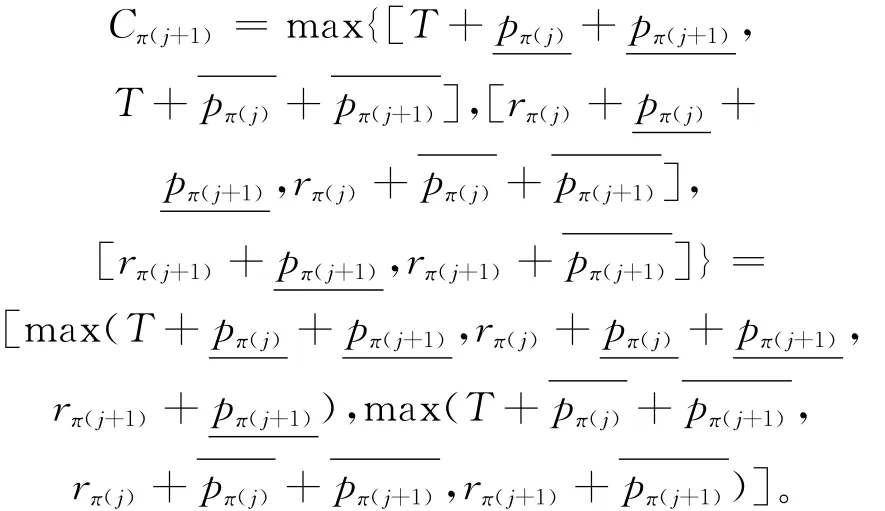
在调度规则S′下π的前j＋1个作业的最大完工时间为：

由rπ（j）＞rπ（j＋1），得，利用乐观准则和悲观准则均得到，所以Cπ（j＋1）＞C′π′（j＋1），当在S下j取集合｛1，2，…，n－1｝中的不同值时，得到在S′下前j＋1个作业的目标函数值小于规则S下的目标函数值，这与最优调度规则S的最优性相矛盾。从而定理2得证。

由定理2不难看出，作业释放时间为实数时，单机最大完工时间最小化问题并没有因加工时间的模糊化而增大问题的难度。然而，当作业的释放时间为区间模糊数，特别是当各作业释放时间区间存在覆盖时，由定义5，此时无法严格比较模糊数的大小，因此无法直接获得最优方案。

问题P3、P4的乐观算法（Optimistic Earliest Release Date firstly，OERD）步骤如下：

（1）将各作业按照释放时间的dopt1值非降进行排 序，使 得dopt1（rπ（1））≤dopt1（rπ（2））≤ … ≤dopt1（rπ（n））。对于1≤k＜k＋m≤n，dopt1（rπ（k））＝dopt1（rπ（k＋1））＝…＝dopt1（rπ（k＋m）），则将此m＋1个作业根据释放时间的dopt2值非降进行排序，使得dopt2（rπ（k））≤dopt2（rπ（k＋1））≤ … ≤dopt2（rπ（k＋m））。从而得到乐观决策方案π。

（2） 令Sπ（1）＝rπ（1）；Cπ（1）＝Sπ（1）＋pπ（1）；对于 （j＝2；j≤n；j＋＋）｛Sπ（j）＝ max（Cπ（j－1），rπ（j））；Cπ（j）＝Sπ（j）＋pπ（j）；｝。

（3）返回乐观决策方案π及其对应最大完工时间Cπ（n）。

问题P3、P4的悲观算法（Pessimistic Earliest Release Date firstly，PERD）步骤如下：

（1）将各作业按照释放时间的dpes1值非降进行排 序，使 得dpes1（rπ（1））≤dpes1（rπ（2））≤ … ≤dpes1（rπ（n））。如 果 对 于 1≤k＜k＋m≤n，dpes1（rπ（k））＝dpes1（rπ（k＋1））＝…dpes1（rπ（k＋m）），则将此m＋1个作业根据释放时间的dpes2值非降进行排序，使 得dpes2（rπ（k））≤dpes2（rπ（k＋1））≤ … ≤dpes2（rπ（k＋m））。从而得到悲观决策方案π。

（2） 令Sπ（1）＝rπ（1）；Cπ（1）＝Sπ（1）＋pπ（1）；对于 （j＝2；j≤n；j＋＋）｛Sπ（j）＝ max（Cπ（j－1），rπ（j））；Cπ（j）＝Sπ（j）＋pπ（j）；｝。

（3）返回悲观决策方案π及其对应最大完工时间Cπ（n）。

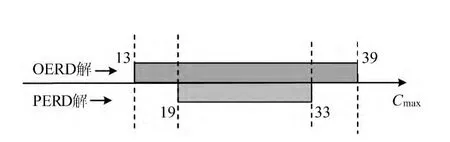
图3 OERD算法与PERD算法比较

观察上面为不同态度的决策者提出的不同算法，若将释放时间改为确切实数，则问题变为问题P2；若将加工时间也变为确切实数，则问题简化为P1。若释放时间变为确定的实数，则相应的算法退化为ERD算法。

定理3 对于问题P3、P4，设OERD算法获得的最大完工时间为，PERD算法获得的最大完工时间为，则。即，乐观算法OERD对应的解的模糊区间长度不小于悲观算法PERD解的模糊区间长度，且OERD解的模糊区间覆盖了PERD解的模糊区间。

证明 简证之。由于OERD算法依据乐观规则，决策者以模糊释放时间的下限为决策依据，从而可知对于任意其他调度方案，其下限值均不小于OERD算法解，因此。同理，PERD算法依据悲观规则，所以对于任意其他调度方案，其上限值均不小于PERD算法解，因此。显然。从而定理3得证。

4 算 例

本节通过算例验证前面对问题P4的分析结论。问题P3可以看作问题P4的特例，其中对任意的上下限相同，即。假设共有8个作业需要加工，在调度之前对各作业的释放时间与加工时间进行预测，预测值均用区间模糊数表示，各作业释放时间与加工时间参数取值见表1所列。

由于上述算例属于P4问题，因此不同决策偏好的决策者会选择不同的调度方法。表2、表3所列分别为OERD算法与PERD算法的解。

针对该算例，通过比较乐观算法OERD和悲观算法PERD的决策方案，能够更加直观地验证定理3的结论，比较结果如图3所示。

由图3可知，现实中乐观决策者依据乐观准则进行决策，然而其渴望获得非常优的结果（算例中获得［13，19］区间的最大完工时间）的同时，也存在着获得很差结果（最大完工时间落在［33，39］区间）的风险。另外，悲观决策者依据悲观准则进行决策，其解的模糊程度（这里是模糊区间的长度）比乐观决策方案小，因此悲观决策方案往往对应于有精确偏好的决策方案，这种情况与现实也是相符的。虽然乐观决策方案与悲观决策方案有很大区别，但是在针对具体的实际调度问题时，由于参数最终取值的不同会使得两者优劣发生变化。并且，由于OERD与PERD算法均是事前决策，因此采用事后评价时，两者未必能够获得具体调度问题的最优解。

针对上述算例，给出3组不同的参数取值，见表4所列，说明2种算法调度方案以及实际问题最优调度方案的不同。

对于上述P4问题，由于参数取值的不确定性存在于事前，即作业尚未加工之时，因此针对模糊参数的决策方法OERD与PERD所获得的作业加工次序对参数不同取值均是不变的。而由于采用事后评价，在作业加工之后对调度方案进行评价，此时每个作业具有确定的参数取值，因此可用ERD规则求解相应的P1问题，并且对于不同的参数取值，实际的最优决策方案可能对应不同的作业加工次序。另外，由于模糊性对决策者的干扰，对于不同的最终参数取值OERD与PERD算法解的质量都会发生变化，并且难以达到实际的最优化。

表1 调度前作业参数预测值

表2 乐观算法OERD调度方案的解

表3 悲观算法PERD调度方案的解

表4 不同参数最终取值对解的影响

?

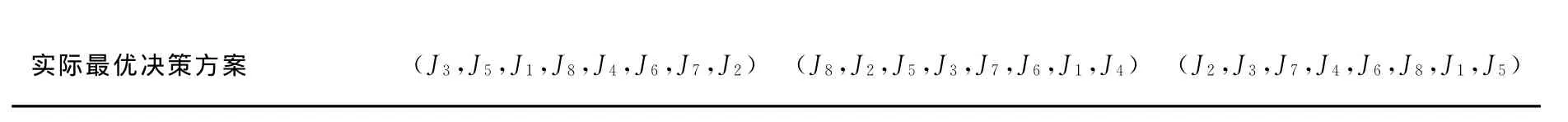
5 结束语

本文重点研究了作业释放时间与加工时间同时为区间模糊数的最小化最大完工时间的单机调度问题P4，同时也考虑了释放时间或加工时间其中一者为区间模糊数而另一者为确定实数的特殊情形P3与P2。为了实现问题的求解，定义了区间模糊数的max运算。释放时间与加工时间均为确定实数时问题P1能够通过ERD规则获得最优解。基于此经典理论，证明了ERD规则对问题P2仍然适用。同时为具有不同偏好的决策者构建了问题P3与P4的乐观算法OERD和悲观算法PERD，证明了2种不同决策方案的特征及其相互之间的关系，数值算例验证了理论分析的正确性。本文的进一步工作是重点考虑对具有模糊释放时间的平行机调度问题进行求解。

［1］ Wang C，Wang D，Ip W H，et al.The single machine ready time scheduling problem with fuzzy processing times［J］.Fuzzy Sets and Systems，2002，127：117－129.

［2］ Ahmadizar F，Hosseini L.Single－machine scheduling with a position－based learning effect and fuzzy processing times［J］.International Journal of Advanced Manufacturing Technology，2011，56：693－698.

［3］ Peng J，Liu B.Parallel machine scheduling models with fuzzy processing times［J］.Information Sciences，2004，166：49－66.

［4］ Balin S.Parallel machine scheduling with fuzzy processing times using a robust genetic algorithm and simulation［J］.Information Sciences，2011，181：3551－3569.

［5］ Lai P J，Wu H C.Evaluate the fuzzy completion times in the fuzzy flow shop scheduling problems using the virus－evolutionary genetic algorithms［J］.Applied Soft Computing，2011，11：4540－4550.

［6］ Lei D.A genetic algorithm for flexible job shop scheduling with fuzzy processing time［J］.International Journal of Production Research，2010，48（10）：2995－3013.

［7］ Lei D.Co－evolutionary genetic algorithm for fuzzy flexible job shop scheduling［J］.Applied Soft Computing，2012，12：2237－2245.

［8］ 李 平，顾幸生.不确定条件下不同交货期窗口的Job Shop调度［J］.管理科学学报，2004，7（2）：22－26.

［9］ Chanas S.，Kasperski A.On two single machine scheduling problems with fuzzy processing times and fuzzy due dates［J］.European Journal of Operational Research，2003，147：281－296.

［10］ Itoh T，Ishii H.One machine scheduling problem with fuzzy random due－dates［J］.Fuzzy Optimization and Decision Making，2005，4：71－78.

［11］ 吴 悦，汪定伟.用遗传算法解模糊交货期下Flow Shop调度问题［J］.系统工程理论与实践，2000，20（2）：108－112.