基于主成分分析法的车险定价因子研究

刘征宇， 夏 伟， 刘宁波， 张 利

（1.合肥工业大学 机械与汽车工程学院，安徽 合肥 230009；2.合肥工业大学 安全关键工业测控技术教育部工程研究中心，安徽 合肥

230009；3.合肥工业大学 计算机与信息学院，安徽 合肥 230009；4.蚌埠学院 计算机科学与技术系，安徽 蚌埠 233030）

车险是指对机动车辆由于自然灾害或意外事故所造成的人身伤亡或财产损失负赔偿责任的一种商业保险。根据文献［1］，2012年我国车险行业的保费收入为4 005亿人民币。

目前我国的车险计算基本以车辆价格、吨位、座位数等自然属性和驾驶人的年龄、性别等信息作为计算保费的依据，缺乏直接涉及行车安全的定价因子，存在大部分安全驾驶员为少数高风险驾驶员买单的不合理现状［2］。

随着车联网技术的发展，其与车险行业的结合成为一种趋势。在保险车联网的基础上，本文对车险行业定价因子的获取进行了研究。车联网可以为车险行业提供车辆性能状态、驾驶员驾驶习惯和驾驶时间等信息，再结合主成分分析算法进行去相关性和降维处理，从而为车险行业筛选更有效的定价因子数据。

1 影响行车安全的风险因子

投保车辆发生事故后的索赔金额除了与车辆的自然属性，如价格、吨位等有关外，还与车辆的性能状态、驾驶人员的驾驶行为习惯、道路环境等因素相关，而这些因素恰恰是车辆发生事故的主要原因。本文根据国外成功经验［3－4］，并结合对车险定价因素的研究，提出2类可控风险因素：车辆的性能状态和驾驶人员的驾驶习惯。

影响行车安全的车辆性能状态主要有汽车的动力系统性能、制动系统性能、传动系统性能和转向系统性能等［5］；而驾驶人员的驾驶习惯主要包括加速、减速及是否疲劳驾驶等。本文依据可采集的车载诊断系统信息和GPS数据，选择以下风险因子，见表1所列。

表1 风险因子

为反映车辆的性能状态和驾驶人员的驾驶习惯，选取12个风险因子作为车险行业的定价因子。在主成分分析法的基础上设计基于指标重要性权值的主成分分析法，使用此方法对风险因子进行降维操作，获得可以表征车辆性能状态和驾驶人员驾驶习惯的4个主成分，作为应用于车险行业的定价因子。

2 基于指标重要性权值的主成分分析法

2.1 主成分分析法

主成分分析（principal component analysis，PCA）是一种对多指标数据进行处理的技术，这种方法可以有效地找出数据中最主要的元素和结构，去除噪音和冗余，将原有的多指标数据降维，而又保留原数据包含的大部分信息［6］。其几何思想如图1所示：设有一组二维数据，坐标系为x1、x2，二维数据分布在一个椭圆形的区域中。定义椭圆形的长轴为F1，短轴为F2。从图中可以看出，在短轴F2方向，数据变化很小；在长轴F1方向上，数据的差值较大，反映的数据样本信息也较多。假设短轴缩小一点时，二维数据就可以采用长轴上的数据进行表示。旋转坐标系，使坐标轴x1、x2与长轴F1、短轴F2重合，此时忽略F2方向的数据，将二维数据向F1方向投影，所得即为主成分。

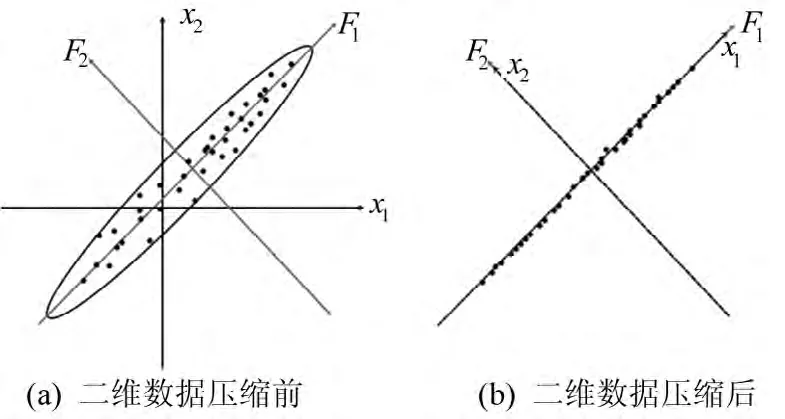
图1 主成分分析法的几何思想

虽然主成分分析法在统计分析、模式识别、图像处理等方面获得了广泛应用，但仍然有其局限性，例如对异常数据的敏感性和对高斯分布的局限性［7］。对此，文献［8］提出了基础分簇的PCA算法，而本文主要考虑各指标数据的重要性差异。

传统的主成分分析方法采用数据方差的大小作为选择主成分的依据，而对各指标数据的重要性并无涉及。此方法对指标重要性相同的应用，例如图像处理，并无影响；而对指标重要性不相同的应用，例如涉及行车安全的各指标分析，就存在将方差比较小的重要指标数据去除的情况。因此本文提出基于指标重要性权值的主成分分析方法，对各指标赋予不同的权值，以对主成分分析结果进行调整。各指标的权重采用层次分析法（analytic hierarchy process，AHP）获得。

2.2 层次分析法获取指标重要性权值

层次分析法把复杂问题中的各种指标通过划分为相互联系的有序层次，使之条理化，根据人们对一定客观现实的主观判断建立判断矩阵。而后，通过排序计算和一致性检验反映每一层次元素相对重要性次序的权值［9］。其实现过程如下。

（1）建立层次结构模型。将决策的目标、决策考虑的准则和实现方案分为最高层、中间层和最低层，建立层次结构模型。

（2）构造判断矩阵。设判断矩阵为：

由于指标较多，因此不能将所有指标放在一起比较，而是两两进行比较。判断矩阵用于标注2个指标两两比较时的相对重要性值，该值使用Santy提出的1～9标度方法给出，见表2所列。

如果判断矩阵A满足aij＝aikakj，则称A为一致阵；而当矩阵A不一致时，需对不一致的范围进行检验。

（3）层次单排序及其一致性检验。层次单排序就是把本层所有各元素对上一层排出评比顺序，这就要在判断矩阵上进行计算，最常用的计算方法有和积法和方根法。一致性检验是为了将A的不一致程度控制在允许范围之内。

2.3 基于指标重要性权值的主成分分析法

设有m个样本，每个样本有n个指标数据，这样就构成了一个Xij（i＝1，2，…，m；j＝1，2，…，n）的样本矩阵，记Xj为X的第j个列向量。在本文的仿真验证中，n个指标为12个风险因子，m个样本为10组样本数据。

（1）采用上述的层次分析法获得各指标的重要性权值W＝［w1，w2，…，wn］，将此权值作为主成分分析的依据，参与主成分的降维过程。

（2）为了消除各指标量纲的影响，使用（1）式对样本数据矩阵进行标准化处理，使各指标数据均值为0，方差为1。

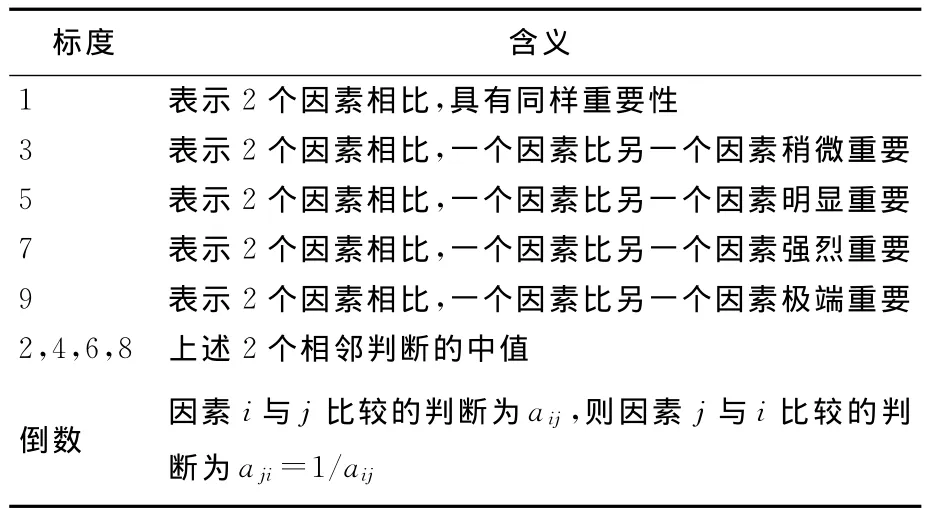
表2 判断矩阵元素的标度方法

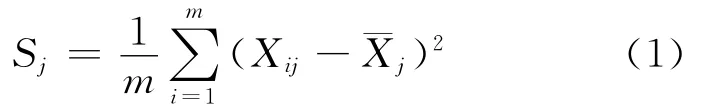
（3）使用（3）式建立标准化矩阵Y的相关系数矩阵C。在相关系数矩阵中，对角线元素表示各个指标的方差，其余元素表示2个指标的相关系数。

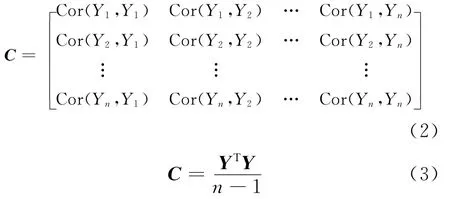
（4）使用指标重要性权值Wi对相关系数矩阵C进行调整，如（4）式。在主成分分析中，以各指标数据的方差作为降维的依据，（4）式使用指标重要性权值对各指标数据的方差做替换，使权值参与主成分的降维过程。

（5）特征值分解。矩阵C为对称矩阵，将C对角化，即对C进行特征值分解，得到特征值，记为λ1＞λ2＞…＞λm（m≤n），组成特征值矩阵Λ；特征向量单位正交化组成矩阵A，则有ATCA＝Λ…

在特征值矩阵Λ中，其对角线元素λ1，λ2，…，λm是各指标去除相关性后的方差，代表了各指标实际携带信息的多少，以此作为主成分选择的依据。令。则称Sk为第k个主成分的贡献率，Tk为前k个主成分的贡献率。

对主成分个数的确定有2种策略：

（1）均数法。计算特征值的均数，取λ大于均数的主成分。

（2）经验法。当Tk达到一定程度（如80%～95%）时，取前k个主成分。

获得主成分：Zi＝a1iY1＋a2iY2＋…＋aniYn。

3 基于AHP的车险行业定价因子确定

由于目前车险车联网的思想尚未在国内得到应用，车险公司也未采集相关的风险因子数据，为说明本方法的可操作性，本文设计了一套车载信息采集终端，用于从车载诊断系统读取相关数据。风险因子数据由车载信息采集终端获得的原始数据计算得到，采集周期为1个行程（从发动机启动到关闭），以在10台车辆上采集的数据作为分析依据。数据如下所示：

3.1 计算风险因子的重要性权值

对风险因子重要性权值的计算采用称为Yaahp的层次分析软件。Yaahp（Yet Another AHP）是欣晟允软件技术有限公司开发的一个层次分析法（AHP）软件，提供方便的层次模型构造、判断矩阵数据录入、排序权重计算以及计算数据导出等功能。

（1）风险因子的层次结构模型。建立关于风险因子的层次结构模型如图2所示。在此模型中，主要为确定各风险因子相对于驾驶风险的重要性权值，所以将风险因素作为准则一层，风险因子作为对应的准则二层；为了模型的完整性，在此选择驾驶风险作为目标层，驾驶人员1、驾驶人员2作为方案层，对本次分析来说，方案层无意义。

图2 风险因子的层次结构模型

（2）风险因子的判断矩阵。构造本模型的层次间判断矩阵。判断矩阵分为2层，第1层为车辆性能状态相对驾驶行为习惯的标度；第2层分为2个矩阵，包括车辆性能状态相关风险因子的两两相对标度，即

和驾驶行为习惯相关风险因子的两两相对标度，即

最后采用和积法计算各个权向量，并通过一致性检验，获得2个风险因素，12个风险因子的重要性权值，见表3所列。

表3 风险因子权值

3.2 确定定价因子

采用本文提出的基于重要性权值的主成分分析方法，按照图3所示流程，运用Matlab软件对采集到的数据进行降维处理［10］，其中风险因子的重要性权值在3.1节中获得。

图3 基于指标重要性权值的主成分分析法流程图

最后得到主成分的特征值如图4所示。主成分分析结果见表4所列，前4个主成分的贡献率已经达到88.82%，说明这4个主成分基本包含了全部12项因子所具有的信息。故最终的定价因子选择此4个主成分，定价因子数据由公式Z＝YAk（Ak为前4个特征值对应的特征向量矩阵）获得。

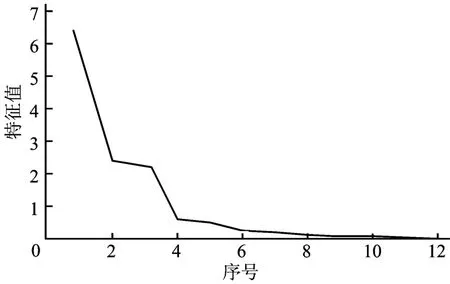
图4 主成分特征值

表4 主成分因子的特征值、贡献率

4 结束语

本文主要对车险行业的定价因子进行研究。在可获得数据的基础上，结合相关资料，选择车辆的性能状态和驾驶人员的驾驶习惯2类风险因素、12个风险因子。采用改进的主成分分析法对风险因子数据进行降维处理，获得4个能为车险行业提供有效定价依据的主成分因子。

［1］ 中国保险年鉴编委会.中国保险年鉴2013［R］.北京：中国保险年鉴社，2013.

［2］ 杨世东.我国汽车保险理赔中存在问题及对策研究［J］.现代经济信息，2011（9）：185－188.

［3］ Xie Chengqiu，Parker D.A social psychological approach to driving violations intwo Chinese cities［J］.Transportation Research Part F，2002：293－308.

［4］ 李平凡.驾驶行为表征指标及分析方法研究［D］.吉林：吉林大学交通学院，2010.

［5］ 夏均忠.汽车综合性能检测［M］.北京：机械工业出版社，2011：3－5.

［6］ Eriksson L，Johansson E，Wold S.Multi－and megavariate data analysis［M］.Umea：Umetrics AB，2006：19－25.

［7］ Sato－Ilic M，Jain L C.Innovations in fuzzy clustering［M］.Springer－Verlag New York Inc，2006：30－34.

［8］ Heo G，Gader P，Frigui H.Robust kernel PCA using fuzzy membership［C］／／Proceedings of International Joint Conference on Neural Networks，2009：1213－1220.

［9］ Liu F H F，Hai H L.The voting analytic hierarchy process method for selecting supplier［J］.International Journal of Production Economics，2005，97（3），308－317.

［10］ 吴 鹏.MATLAB高效编程技巧与应用［M］.北京：北京航空航天大学出版社，2010：197－212.